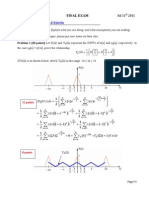
Professional Documents
Culture Documents
The Vasicek Model
Uploaded by
Sanket PatelCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
The Vasicek Model
Uploaded by
Sanket PatelCopyright:
Available Formats
The Vasicek Model
Bjrn Eraker
Wisconsin School of Business
February 11, 2010
Bjrn Eraker Vasicek Model
The Vasicek Model
The Vasicek model (Vasicek 1978) is one of the earliest
no-arbitrage interest rate models.
It
is based upon the idea of mean reverting interest rates
gives an explicit formula for the (zero coupon) yield curve
gives explicit formulaes for derivatives such as bond
options
can be used to create an interest rate tree
Bjrn Eraker Vasicek Model
AR(1) Processes
An autoregressive process of order 1 (AR(1)) is a stochastic
process of the form
Y
t
= a + bY
t1
+
t
where a and b are constants,
t
is a random error term, typically
t
N(0,
2
)
Bjrn Eraker Vasicek Model
Features of the AR(1)
If b = 1, the process is a random walk
If b = 0 then Y
t
is just white noise
If 0 < b < 1 the process is said to be mean-reverting.
The parameter b measures the persistence in Y
t
and 1 b
is called the speed of mean-reversion.
Parameters a, b can be found by a regression of Y
t
on
Y
t1
.
b literarily is the autocorrelation of Y
t
since
b =
Cov(Y
t
, Y
t1
)
Var(Y
t1
)
=
Cov(Y
t
, Y
t1
)
Std(Y
t1
)Std(Y
t
)
= Corr(Y
t
, Y
t1
)
since Std(Y
t1
) = Std(Y
t
).
Bjrn Eraker Vasicek Model
Mean Reversion
If a process is mean reverting, it tends to revert to a
constant, long run mean
The speed of mean reversion measures the average time it
takes for a process to revert to its long run mean
Mean reversion is reasonable for interest rates - random
walk makes no sense because it is economically
unreasonable to think that interest rates can "wander of to
innity" or become arbitrarily large.
So what is the typical speed of mean reversion in interest
rates? Weekly data gives 0.9961 for 3m T-bills. This is
extremely high persistence and indicates that interest rates
are close to random walk...
Bjrn Eraker Vasicek Model
The Short Rate
Many term structure models, including Vasiceks, assume that
the fundamental source of uncertainty in the economy is the
short rate.
The short rate is the annualized rate of return on a very short
term investment (lets assume daily).
Bjrn Eraker Vasicek Model
The Vasicek Model
The Vasicek model simply assumes that the short rate, r
t
follows an AR(1),
r
t
= a + br
t1
+
t
. (1)
That is, Vasicek just assumes a purely statistical model for the
evolution of interest rates.
Bjrn Eraker Vasicek Model
Alternative Representations
The model is sometimes written,
r
t
= ( r
t1
)t + z
t
(2)
where
r
t
= r
t
r
t1
(3)
and z
t
is a normally distributed error term.
Using the denition of r
t
, and set t = 1, we have
r
t
= + (1 )r
t1
+ z
t
(4)
which is an AR(1) if a = and b = 1 .
Bjrn Eraker Vasicek Model
We can also set t to something different from 1. In this case
we assume that
z N(0, t )
Bjrn Eraker Vasicek Model
Differential Notation
Tuckman writes
dr
t
= ( r
t
)dt + dw
t
This is a stochastic differential equation where dw is Brownian
motion. You should interpret it to mean
r
t
= ( r
t1
)t + z
t
(5)
In other words, we interpret dr
t
to mean r
t
= r
t
r
t1
.
Therefore, any time you see a the differential notation in
Tuckman, translate by equating to the rst difference.
Bjrn Eraker Vasicek Model
Vasicek Zero Coupon Curve
Let B(t , T) denote the time t price of a zero coupon bond with
maturity date T. It is
B(t , T) = exp(A(t , T)r
t
+ D(t , T)) (6)
A(t , T) =
1 e
(Tt)
(7)
D(t , T) =
2
2
[A(t , T) (T t )]
2
A(t , T)
2
4
(8)
In other words, the Vasicek model gives us an exact expression
for the value of a zero coupon. We can compare this to other
models for zero coupon bond prices, such as the cubic spline
model and Nelson-Siegel.
Bjrn Eraker Vasicek Model
Properties of the Vasicek term structure
Lets take some example parameter values to see how the
Vasicek term structure behaves. Reasonable values are
= (1 0.9961) 52 0.2,
= 0.0025
52 0.018,
(180 basis p/ year) and
= 0.05
(the average risk free rate).
Bjrn Eraker Vasicek Model
Effects of mean reversion
The smaller the mean reversion in interest rates, the more
we expect interest rates to remain close to their current
levels.
If we expect interest rates to change very slowly, long
dated bonds tend to move in parallel to short.
Thus, higher (lower) speed of mean reversion ( = 1 b)
lead to a steeper (less steep) term structure because the
term structure depends on future expected short rates
(illustrated on next slide)
Bjrn Eraker Vasicek Model
Vasicek Bond Options
Consider an option on a zero coupon. The underlying bond has
maturity T and the option matures at T
0
(we assume T
0
< T
why?).
The value of a call option with strike K is
C = B(t , T)N(d
1
) KB(t , T
0
)N(d
2
) (9)
where d
1
and d
2
have expressions that mimic those in the
Black-Scholes model.
Bjrn Eraker Vasicek Model
Building a Vasicek Tree
We will try to build an interest rate tree which is consistent
with the assumed short rate dynamics in the Vasicek
model.
We will build a monthly model.
Assume the following parameters: = 0.025 (k in
Tuckman), = 0.0126, and = 0.15339.
Lets assume that the current short rate is 5.121% and also
that the probability of going up/down in the rst month is
1
2
.
Bjrn Eraker Vasicek Model
Lets try to build a tree by setting z
t
= +1 with probability
1
2
.
Our tree will look something like
r
0
r
u
1
r
d
1
where
r
u
1
= r
0
+ ( r
0
)/12 +
12
= 5.506%
and
r
d
1
= r
0
+ ( r
0
)/12
12
= 4.7786%
Bjrn Eraker Vasicek Model
We should verify that
E(r ) = ( r
0
)/12
and
Std(r ) =
12
which follows trivially here.
Bjrn Eraker Vasicek Model
Next, lets try the same for the the next period in the tree....
If in the down-state (r
1
= r
d
1
= 4.7786%) at t=1, we get that the
up move should equal
r
ud
2
= r
d
1
+ ( r
d
1
)/12 + /
12 = 5.1643%
and likewise, if in the up-state, we get that the down move
should be
r
du
2
= r
u
1
+ ( r
u
1
)/12 + /
12 = 5.1628%
Bjrn Eraker Vasicek Model
In other words, our interest rate tree is
5.121%
5.506%
4.7786%
5.8902%
5.1628%
5.1643%
4.4369%
Bjrn Eraker Vasicek Model
Designing a recombining tree
We need a recombining three such to avoid too many branches
when we add time-steps.
Lets consider relaxing the 50/50 probability assumption. If we
do, we also need to adjust the rate in the up-up and down-down
to maintain the correct mean and variance of the future interest
rate.
The tree is
5.121%
5.506%
4.7786%
r
uu
5.1635%
r
dd
Bjrn Eraker Vasicek Model
where we assign a probabilities p and q of an up move
conditional upon being in either state.
The number 5.1635 on the middle branch is the expected value
of the interest rate after two periods.
The expected value after one period is
5.121 + 0.025(15.339 5.121)/12 = 5.1423
the expected value of the interest rate in period 2 is
5.1423 + 0.025(15.339 5.1423)/12 = 5.1635
Bjrn Eraker Vasicek Model
We now solve for r
uu
, r
dd
, p and q using the mean and
variances in the following way. Consider p and r
uu
:
The expected future value given an up move in period 1 is
5.506 + 0.025(15.339 5.506)/12 = 5.5265
This means that our binomial tree must give
p r
uu
+ (1 p)5.1635 = 5.5265
Bjrn Eraker Vasicek Model
Secondly, we know that the standard deviation is
0.0126/
12 = 0.003637 per month so we should have
p(r
uu
5.5265%)
2
+(1p)(5.1635%5.5265%)
2
= 0.3637%
We now have two equations in two unknowns and we nd
p = 0.499
and
r
uu
= 5.8909%.
Bjrn Eraker Vasicek Model
We solve for q and r
dd
using the same technique. We get
q = 0.5011 and r
dd
= 4.4361%, giving the recombining tree
5.121%
5.506%
4.7786%
5.8909%
5.1635%
4.4361%
Bjrn Eraker Vasicek Model
Next...
... we nd the nodes in month 4. The method is entirely
analogous to what is we did at time 3 (see Tuckman p. 238).
Bjrn Eraker Vasicek Model
5.121%
5.506%
4.7786%
5.8909%
5.1635%
4.4361%
r
uuu
5.5484%
5.8210%
r
ddd
Bjrn Eraker Vasicek Model
Here the two middle branches are assigned
1
2
probabilities
while the move from 5.8909 and up is assigned probability p
and the 4.4361% to 5.8210% is assigned probability q.
We now solve for r
uuu
, p and r
ddd
, q in as at time t = 3.
Bjrn Eraker Vasicek Model
Concluding remarks
Even with the Vasicek model, we need to solve non-linear
equations to construct the tree
More complicated models typically imply that we need to
solve even more complicated equations.
Shortcomings of the Vasicek model:
Interest rate can become negative
Difcult to make the model t the yield curve exactly (spot
rate function is not exible enough)
Constant local volatility is not realistic, but it is easy to
generalize...
Numerous generalizations are possible... stay put
Bjrn Eraker Vasicek Model
You might also like
- A Course in Math Bio SolDocument63 pagesA Course in Math Bio SolItzalá Mendoza100% (10)
- Hw4 Mfe Au14 SolutionDocument7 pagesHw4 Mfe Au14 SolutionWenn ZhangNo ratings yet
- Stock Prices, Asset Portfolios and Macroeconomic Variables in Ten European CountriesDocument24 pagesStock Prices, Asset Portfolios and Macroeconomic Variables in Ten European CountriesMario CruzNo ratings yet
- Free Fall Colla'seDocument3 pagesFree Fall Colla'sesendra20No ratings yet
- Lehman - Can Convexity Be ExploitedDocument15 pagesLehman - Can Convexity Be Exploitedmsk_196412100% (1)
- DSP1 - Practice Homework With SolutionsDocument9 pagesDSP1 - Practice Homework With Solutionsdania alamenNo ratings yet
- LogisticDocument11 pagesLogisticankitNo ratings yet
- SIMPLE AlgorithmDocument13 pagesSIMPLE AlgorithmprabumnNo ratings yet
- Ee132b Hw1 SolDocument4 pagesEe132b Hw1 SolAhmed HassanNo ratings yet
- TMRCA EstimatesDocument9 pagesTMRCA Estimatesdavejphys100% (1)
- Partial Differential EquationDocument9 pagesPartial Differential EquationEng Shakir H100% (1)
- Signals, Linear Systems, and ConvolutionDocument18 pagesSignals, Linear Systems, and ConvolutionmarriyumNo ratings yet
- Accounting Textbook Solutions - 74Document18 pagesAccounting Textbook Solutions - 74acc-expertNo ratings yet
- Multiple ChoiceDocument3 pagesMultiple ChoicePeng GuinNo ratings yet
- Abbas MCQDocument10 pagesAbbas MCQRUBAB IQBALNo ratings yet
- Principals of Risk Interest Rate ScenariosDocument38 pagesPrincipals of Risk Interest Rate ScenariosBob TaylorNo ratings yet
- Chapter 08 Interest Rates and Bond ValuationDocument40 pagesChapter 08 Interest Rates and Bond ValuationHuu DuyNo ratings yet
- Vasicek Model SlidesDocument10 pagesVasicek Model SlidesnikhilkrsinhaNo ratings yet
- Discrete-Time Evaluation of The Time Response: AppendixDocument6 pagesDiscrete-Time Evaluation of The Time Response: AppendixAnonymous WkbmWCa8MNo ratings yet
- Three Period OLGDocument12 pagesThree Period OLGDavidChum Lai100% (1)
- Green's Functions For The Stretched String Problem: D. R. Wilton ECE DeptDocument34 pagesGreen's Functions For The Stretched String Problem: D. R. Wilton ECE DeptSri Nivas ChandrasekaranNo ratings yet
- Ito ProcessDocument76 pagesIto ProcessAdrian d'AuvergneNo ratings yet
- Direct and Indirect Approaches For Solving Optimal Control Problems in MATLABDocument13 pagesDirect and Indirect Approaches For Solving Optimal Control Problems in MATLABBharat MahajanNo ratings yet
- 1 Exy 1 SDocument11 pages1 Exy 1 SLukas BoskoNo ratings yet
- CS 229, Autumn 2012 Problem Set #1 Solutions: Supervised LearningDocument16 pagesCS 229, Autumn 2012 Problem Set #1 Solutions: Supervised LearningAvinash JaiswalNo ratings yet
- EE341 FinalDocument4 pagesEE341 FinalLe HuyNo ratings yet
- 2011 Exam - Financial MathematicsDocument6 pages2011 Exam - Financial MathematicsSylvia HuynhNo ratings yet
- Emmanuel GincbergDocument37 pagesEmmanuel GincbergLameuneNo ratings yet
- Counting Probability of Dice Tossing One Two and Three in MatlabDocument4 pagesCounting Probability of Dice Tossing One Two and Three in MatlabJans HendryNo ratings yet
- DSP, DAIICT by PRof Aditya TatuDocument4 pagesDSP, DAIICT by PRof Aditya TatuChirag GaurNo ratings yet
- FEM Higher Order ElementsDocument28 pagesFEM Higher Order Elementsjoshibec100% (1)
- Math 151 Algebra2016 1Document112 pagesMath 151 Algebra2016 1Lord Ponkor Offin100% (1)
- Xppaut NotesDocument8 pagesXppaut Notescalvk79No ratings yet
- Macroeconomics 1 PS3 Solution PDFDocument10 pagesMacroeconomics 1 PS3 Solution PDFTaib MuffakNo ratings yet
- Statistical Modeling of Extreme Values PDFDocument28 pagesStatistical Modeling of Extreme Values PDFHassanRazaNo ratings yet
- FEMM File FormatDocument5 pagesFEMM File FormatMuhammad HafizeNo ratings yet
- 1.1 Basic Concepts. Modeling: Engineering Problems Physical Problems Economic ProblemsDocument24 pages1.1 Basic Concepts. Modeling: Engineering Problems Physical Problems Economic Problems박태영No ratings yet
- Lab Report 7 Borda PendulumDocument7 pagesLab Report 7 Borda PendulumazarmechNo ratings yet
- (EE332) (09ECE) (Group13) Report ProjectDocument23 pages(EE332) (09ECE) (Group13) Report ProjectNgô ĐạtNo ratings yet
- ControlDocument13 pagesControlNiaz ManikNo ratings yet
- Errata Digital Communications: John G. Proakis and Masoud Salehi Fifth Edition, Mcgraw-Hill, 2008Document3 pagesErrata Digital Communications: John G. Proakis and Masoud Salehi Fifth Edition, Mcgraw-Hill, 2008Rasha ZiyadNo ratings yet
- Solved Examples For Chapter 19Document7 pagesSolved Examples For Chapter 19SofiaNo ratings yet
- (CC297) Série 04 - Fortunato Neto pt2Document7 pages(CC297) Série 04 - Fortunato Neto pt2Fortunato NetoNo ratings yet
- The Fundamental Theorem of Calculus and The Poincaré LemmaDocument13 pagesThe Fundamental Theorem of Calculus and The Poincaré LemmasuperscriberNo ratings yet
- Time Dep SCH EqnDocument33 pagesTime Dep SCH Eqnutkarsh khandelwalNo ratings yet
- CH 2 Solutions - Network SecurityDocument9 pagesCH 2 Solutions - Network Securitykarthikc_625No ratings yet
- Quantum Field Theory Solution To Exercise Sheet No. 9: Exercise 9.1: One Loop Renormalization of QED A)Document20 pagesQuantum Field Theory Solution To Exercise Sheet No. 9: Exercise 9.1: One Loop Renormalization of QED A)julian fischerNo ratings yet
- Solution 2Document5 pagesSolution 2Paulina MarquezNo ratings yet
- CN2116-HW7-Solution (XJP - 2011)Document12 pagesCN2116-HW7-Solution (XJP - 2011)Brian WatsonNo ratings yet
- Homework 4 SolutionsDocument16 pagesHomework 4 SolutionsAE ENo ratings yet
- Dynamics and Differential EquationsDocument30 pagesDynamics and Differential EquationsHusseinali HusseinNo ratings yet
- ch02 PDFDocument108 pagesch02 PDFtoligado27No ratings yet
- 3assignment SolDocument7 pages3assignment SolDalghak KhanNo ratings yet
- Analysis of Runge Kutta MethodDocument40 pagesAnalysis of Runge Kutta MethodAbdul RahimNo ratings yet
- Z-Domain: by Dr. L.Umanand, Cedt, IiscDocument31 pagesZ-Domain: by Dr. L.Umanand, Cedt, IisckarlochronoNo ratings yet
- Hw5 Mfe Au14 SolutionDocument8 pagesHw5 Mfe Au14 SolutionWenn Zhang100% (2)
- Ee263 Ps1 SolDocument11 pagesEe263 Ps1 SolMorokot AngelaNo ratings yet
- Zarchan-Lecture Kalman Filter9Document104 pagesZarchan-Lecture Kalman Filter9larasmoyoNo ratings yet
- Tutorial 01 - Solution Set Problems Discussed in TutorialsDocument6 pagesTutorial 01 - Solution Set Problems Discussed in TutorialsSeNka Nermin MujNo ratings yet
- L8 Dimensional Analysis ChapterDocument36 pagesL8 Dimensional Analysis ChapterDangol RupeshNo ratings yet
- Nyjc h2 Math p2 SolutionDocument11 pagesNyjc h2 Math p2 SolutionjimmytanlimlongNo ratings yet
- 10-Linear Strain Triangle and Other Types of 2d ElementsDocument31 pages10-Linear Strain Triangle and Other Types of 2d Elementskranthi142434No ratings yet
- Engineering Risk Benefit Analysis: CBA 4. Including UncertaintyDocument39 pagesEngineering Risk Benefit Analysis: CBA 4. Including Uncertaintymihai37No ratings yet
- Vasicek Bond PDFDocument15 pagesVasicek Bond PDFLe Hoang VanNo ratings yet
- Numerical Implementation of Hull-White Interest Rate ModelDocument6 pagesNumerical Implementation of Hull-White Interest Rate ModelYigal Ben TalNo ratings yet
- 3 Fall 2007 Exam PDFDocument7 pages3 Fall 2007 Exam PDFAchilles 777No ratings yet
- Financial Economics (HE54) : Course ObjectiveDocument3 pagesFinancial Economics (HE54) : Course ObjectiveSakshi SharmaNo ratings yet
- Conceptual FrameworkDocument5 pagesConceptual FrameworkSomaskhandan ChinnasamyNo ratings yet
- JPM MBS PrimerDocument68 pagesJPM MBS PrimerJerry ChenNo ratings yet
- SPL AssignmentDocument2 pagesSPL AssignmentArchana MantriNo ratings yet
- ACI Diploma Sample QuestionsDocument7 pagesACI Diploma Sample Questionsattractram100% (1)
- Chap005a - The Value of BondDocument35 pagesChap005a - The Value of Bondnt.phuongnhu1912No ratings yet
- ModelingDerivatives GalleyDocument268 pagesModelingDerivatives Galleygdellanno100% (1)
- Chapter 13 Economy Market AnalysisDocument11 pagesChapter 13 Economy Market AnalysisAli HussainNo ratings yet
- Mancon Quiz 4Document32 pagesMancon Quiz 4Quendrick SurbanNo ratings yet
- Case - Ohio Rubber Works Inc PDFDocument3 pagesCase - Ohio Rubber Works Inc PDFRaviSinghNo ratings yet
- Chap3 Present ValueDocument26 pagesChap3 Present ValueGonzalo Martinez100% (1)
- The U.S. Treasury Yield Curve: 1961 To The Present: Refet S. Gu Rkaynak, Brian Sack, Jonathan H. WrightDocument14 pagesThe U.S. Treasury Yield Curve: 1961 To The Present: Refet S. Gu Rkaynak, Brian Sack, Jonathan H. WrightGreta Manrique GandolfoNo ratings yet
- Hull White PDFDocument64 pagesHull White PDFstehbar9570No ratings yet
- Financial Markets and Institutions 9th Edition Mishkin Test BankDocument27 pagesFinancial Markets and Institutions 9th Edition Mishkin Test Bankmichaelkrause22011998gdj100% (34)
- Term Structure Models: VersionsDocument20 pagesTerm Structure Models: VersionsibrahimsouaNo ratings yet
- SPP Capital Market Update July 2023Document10 pagesSPP Capital Market Update July 2023Jake RoseNo ratings yet
- Market Pulse June 2023 2Document173 pagesMarket Pulse June 2023 2devilNo ratings yet
- FIN7520 Notes On Chapter 14 and 15 Bond Prices and YieldsDocument8 pagesFIN7520 Notes On Chapter 14 and 15 Bond Prices and YieldsMichael PironeNo ratings yet
- Bond Yield Curve Holds Predictive PowersDocument15 pagesBond Yield Curve Holds Predictive PowersZuniButtNo ratings yet
- Algorithmic Market Making Strategies PDFDocument81 pagesAlgorithmic Market Making Strategies PDFsahandNo ratings yet
- Guidelines On Banks' Asset Liability Management Framework - Interest Rate RiskDocument35 pagesGuidelines On Banks' Asset Liability Management Framework - Interest Rate RiskMouBunchiNo ratings yet
- To Finance: Fixed Income Securities and Debt MarketsDocument55 pagesTo Finance: Fixed Income Securities and Debt MarketsMoktar Tall ManNo ratings yet
- A Suppose You Are Considering Two Possible Investment Opportunities ADocument1 pageA Suppose You Are Considering Two Possible Investment Opportunities AMuhammad ShahidNo ratings yet