University of Illinois

Spring 2012

ECE 313: Problem Set 8: Problems and Solutions Scaling rule for pdfs, Gaussian distribution, central limit theorem, ML parameter estimation
Due: Reading: Wednesday, March 14 at 4 p.m. ECE 313 Course Notes, Sections 3.63.7.

1. [Exam Grading] Suppose students in a class (not ECE313) take an exam. Assume the exam scores are distributed according to a Gaussian distribution with mean 73 and standard deviation 16. Letter grades are assigned to students according to one of the following grading policies. Policy 1 Scores Grade 85 or more A 65 or more B 45 or more C Less than 45 D Policy 2 Ranking Grade Top 15% A Top 40% B Top 80 % C Not in top 80% D

(a) Using Tables 6.1 and 6.2 in the lecture notes, nd the percentage of students expected to A, B, C, and D under grading policy 1. Solution: Let X be a score of a student. The probability that the score is greater than or equal to 85 is P {X 85} = P X 73 3 16 4 = Q(0.75) = 0.2266.

Thus, 22.66% of students will get A. The probability that the score is greater than or equal to 65 is P {X 65} = P X 73 1 16 2 = Q(0.5) = (0.5) = 0.6915

Since P {65 X < 85} = 0.6915 0.2266 = 0.4649, 46.49% of students will get B. The probability that the score is greater than or equal to 45 is P {X 45} = P X 73 7 16 4 = Q(1.75) = (1.75) = 0.9599

Since P {45 X < 65} = 0.9599 0.6915 = 0.2684, 26.84% of students will get C. Since P {X < 45} = 0.0401, the remaining 4.01% of students will get D. (b) Using the same tables, nd the cut-o scores between A and B, B and C, and C and D under grading policy 2. It is not necessary that the cut-o scores must be integers. Solution: The closest (but no smaller) value in Table 6.1 to 15% is 0.1515. Thus, we have X 73 0.1515 = Q(1.03) = P 1.03 . 16

Thus, to be in top 15%, the score X must be lower bounded by X 73 + 1.03 16 = 89.48. Thus, the cuto score for A is 89.48. Similarly, the closest value in Table 6.2 to 40% is 0.4013. Thus, 0.4013 = Q(0.25) = P X 73 0.25 16

To be in top 40%, the score must be lower bounded by X 73 + 0.25 16 = 77. Thus, the cuto score for B is 77. The closest value in Table 6.1 to 80% is 0.8023. Thus, 0.8023 = (0.85) = Q(0.85) = P X 73 0.85 . 16

To be in top 80%, the score must be lower bounded by X 73 0.85 16 = 59.4 Thus, the cuto score for C is 59.4. 2. [Gaussian Noise] Suppose a wireless communication system consists of a transmitter and a receiver. If the transmitter emits a radio signal with transmission amplitude v , this signal is attenuated by the air and is received by the receiver together with noise, denoted by N . Let Y = v + N be the received signal amplitude, where = 0.01 is the attenuation factor and N is a Gaussian random variable with mean = 0 and variance 2 = 4. (a) Find the pdf fY (u) of the received signal amplitude Y for v = 10. Solution: Y is also a Gaussian random variable with mean v = 0.1 and variance 4. Thus, the pdf of Y is (u 0.1)2 1 fY (u) = exp . 8 8 (b) (Only for this part) Suppose that is unknown, and v and are known to be 10 and 0.01, respectively. If the received signal amplitude Y is 0.03, nd the ML estimator M L of . Solution: For unknown , the pdf of Y at 0.03 is given by fY (0.03) = 1 2 2 exp (0.03 0.1)2 2 2 = 1 2 2 exp 0.072 2 2 .

Taking ln() on both sides, we have 1 1 (0.07)2 ln fY (0.03) = ln 2 ln 2 . 2 2 2 2 2

We now dierentiate the above with respect to 2 as follows 1 (0.07)2 1 d ln(fY (0.03)) = + = 2 2 2 4 d 2 2 2 1 (0.07)2 2 .

(0.03)) Note that d ln(fY is positive if < 0.07 and negative if > 0.07. This means that d the maximum of fY (0.03) is attained at = 0.07. Thus, M L = 0.07.

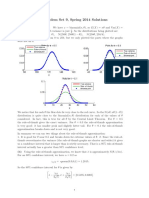
(c) Suppose the transmitter wants to deliver one bit to the receiver using this wireless communication system. If the bit is zero, the transmitter transmits with v = 10. If the bit is one, the transmitter transmits with v = 10. Sketch the distributions of the received signal amplitude Y conditioned on that the bit being zero and conditioned on the bit being one. Solution:
0.20

0.15

0.10

0.05

10

10

(d) Suppose the receiver output is zero if Y < 0 and one if Y 0. An error is said to occur if the receiver output is not equal to the transmitted bit. Find the probability of error, given the transmitted bit is one. Solution: The receiver output will be zero if Y < 0. Thus, P {Y < 0} = P {0.01v + N < 0} = P {N < 0.1} =P N 0.1 2 = Q(0.05) = 0.4801.

3. [Random Walk] Bob and Alice are at the starting point to race toward a goal, which is 10, 000 meters away. A coin is repeatedly tossed 10, 000 times. Each time, if a head comes up, Bob advances one meter. If a tail comes up, Alice advances one meter. (a) Express the distance between Alice and Bob after the 10,000 coin ips in terms of X, where X is the number of times heads shows. Solution: Bob advances X meters, and Alice advances 10000 X meters. Thus, the distance between two is |X (10000 X )| = |2X 10000|. (b) Using the central limit theorem, nd the probability that the distance between Bob and Alice is greater than or equal to 300 meters. (To be denite, you do not need to consider the continuity correction.) Solution: We rst nd the probability that Bob is ahead of Alice by 300 meters or more. Then, the probability that the distance between Bob and Alice is greater than or equal to 300 meters is twice that probability. The probability that Bob is 300 meters or 3

more ahead of Alice is P {2X 10000 300}. Since X is a binomial random variable with mean 5000 and variance 2500, we can apply the central limit theorem as follows: P {2X 10000 300} = P {2X 10300} = P {X 5150} =P X 5000 3 50 Q(3) = 0.0013.

Thus, the probability that the distance between two is greater than or equal to 300 meters is approximately 0.0026. 4. [Evolution of Stock Price] Suppose you bought a stock with a current price Y0 . Let Yt denote your stock price after t days from today (t 0). Everyday, your stock price increases by the factor 1.01 with probability 0.7 or decreases by the factor (1.01)2 with probability 0.3. In other words, the stock price after (t + 1) days is given by with probability 0.7, (1.01)Yt Yt Yt+1 = otherwise. (1.01)2 (a) Let X be the number of days out of the rst 1000 days that the stock price increases. Express the stock price Y1000 after 1000 days in terms of X . Solution: Since the stock price has increased for X days and has decreased for 1000 X days, the stock price is Y1000 = Y0 (1.01)X (1.01)2(1000X ) = Y0 (1.01)3X 2000 .

(b) Find the mean of Y1000 . The formula for (a + b)n in appendix 6.2 might be helpful. Your answer should be a constant times Y0 . Solution: From (a), Y1000 = Y0 (1.01)X (1.01)2(1000X ) . Since X is a binomial random variable with parameters 1000 and 0.7, we can nd the mean of Y using LOTUS as follows:
1000

E [Y1000 ] =

Y0 (1.01)k (1.01)2(1000k) pX (k )
k=0 1000

=Y0

(1.01)k (1.01)2(1000k)
k=0 1000

1000 (0.7)k (0.3)1000k k 0.3 (1.01)2

1000k

=Y0
k=0

1000 (0.7 1.01)k k 0.3 (1.01)2

1000

=Y0 0.7 1.01 +

= 2.969Y0

(c) Using the central limit theorem, nd the probability that you earn 200% or higher prot from the stock, i.e., P {Y1000 3Y0 }. (To be denite, you do not need to consider the continuity correction.) Solution: We rst nd the condition of X to satisfy Y1000 3Y0 . From part (a), we have Y1000 3Y0 Y0 (1.01)3X 2000 3Y0 (1.01)3X 2000 3. (3X 2000) ln 1.01 ln 3 2000 ln 3 X + = = 703.46. 3 ln 1.01 Since X is a binomial random variable with mean 700 and variance 1000 0.7 0.3, we apply the central limit theorem as follows: P {Y1000 3Y0 } = P {X } =P =P 700 X 700 1000 0.7 0.3 1000 0.7 0.3 X 700 0.2394 Q(0.2394) = 0.4054. 1000 0.7 0.3