Bending Induced Stresses

07/11/2012
SHIPPING AND MARINE TECHNOLOGY

DIVISION OF MARINE DESIGN
Lecture 6
CONTENTS:
REPETION: bending-induced stresses Introduction to torsion St Venant torsion theory (see compendium PART A: pp. 48 74)
Definition of simple case study Kinematic relations Constitutive relations Derivation of St Venant torsion moment, shear stress, shear stress flow, etc. Summary of St Venant torsion derivation
Professor Jonas Ringsberg p. 1

Learning objectives

To become familiar with torsion theory applied on ship structures Understand the difference between St Venant and Vlasov torsion theories Know how to calculate St Venant torsion shear stresses for an arbitrary cross-section Understand what the shear stress flow and distribution looks like during pure St Venant torsion loading
07/11/2012

Repetition of bending-induced stresses

General requirements - validity of beam theory

Plane sections of the beam must be plane after deformation Transverse sections must maintain the shape of the section after deformation
Small deformations.
These requirements ensure that the distance between the neutral axis and any longitudinal fiber of the beam is maintained during deformation These requirements can be contained even if we add shear deformation to the problem
07/11/2012

General requirements - validity of beam theory

Beam theory works well also for non-prismatic beams as long as the two main requirements of beam theory are fulfilled The ship deviates from the perfect prismatic beam in many ways, however, due to the shape of the load and load effect the maximum bending moment and the maximum shear forces of the hull will be located between the non-prismatic ends
Therefore, the accuracy of the hull girder concept is very good.
Early efforts to compare full-scale measurements on ships with the beam theory gave very good agreement

Ideal theory vs. measurements
Comparison of full-scale measurements and calculations of bending beam stresses and shear stresses of a single skin tanker.
07/11/2012

Example of stress distributions
Bending shear and normal stress distributions in a transverse section.

Requirements, bending beam theory

Naviers theory
Plane sections remain plane after bending Sections keep the shape after bending Small deformations
This means that the distance to the neutral axis is the same before and after bending for any fiber of the beam
07/11/2012

Bending normal stress

Neutral surface/axis
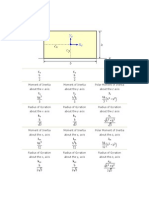
Example: bending with My 0 and Mz = 0 of a straight bar with rectangular cross-section
07/11/2012

Pure bending in two directions

Naviers theory
The strain in a point (y, z) in the cross-section at x is:
= 0 + z y + y z
Hookes law, = E , gives:
N = x dA = E (0 + z y + y z) dA
A A
My = x z dA = E (0 + z y + y z)z dA
A A A A
Mz = x y dA = E (0 + z y + y z)y dA


Naviers theory
The integrals are:
A A
dA = A
y dA = 0, z dA = 0
A 2
y
A
dA = Iz ,
z
A
dA = Iy ,
yz dA = Iyz
A
07/11/2012

Kinematic relation bending deformation


Naviers theory
Normal strain and curvature can be derived as:
0 =
N EA
y =
My I z + Mz Iyz
2 E (Iy Iz Iyz )
z =
My Iyz + M z Iy
2 E (Iy I z Iyz )
The stress in a point (y, z) in the cross-section at x is:
= E = E (0 + z y + y z) = ... = N My (zIz yIyz ) Mz (yIy zIyz ) + 2 A (Iy Iz Iyz )
07/11/2012

Bending shear stress

Shear force

The figure shows bending of a homogeneous and two separate beams Assumption made in engineering beam theory:
Plane sections should remain plane after bending.
07/11/2012

Sheared beam lamina of a homogenous beam
Equilibrium in the x-direction:

+ dx dA dA D dx = 0 x
A
D = b
b is the length of the line in the graph that separates area A from the full transverse section. D is called shear flow (unit: N/m)

Sheared beam lamina of a homogenous beam

dx b b dx
07/11/2012

For thin-walled cross-sections holds:
A The general expression for normal stress gives:
D 1 dA = b b x
N My (zIz yI yz ) Mz (yI y zIyz ) = + 2 x x A (Iy Iz Iyz )

where:
My = Vz x
Mz = Vy x

Integration gives:
D Vz (Sy Iz Sz Iyz ) + Vy (S z Iy Sy Iyz ) = 2 b b(Iy Iz Iyz )

Sy = z dA and S z = y dA are called static moments
where
A A If the y- and z-axis are principal axes, we have:
D Vy S z Vz Sy = + b bI z bIy
10
07/11/2012

The integrals are approximately equivalent with the sums

Static moment of a rectangular cross-section

b
1h h Sy = e A = + z b z 22 2 bh3 Iy = 12 b h2 V z2 2 4 bh3 b 12 3V 2bh

xz =
max =
11
07/11/2012

T-shaped cross-section
V
2
max
D, shear flow

The shear centre (SC)
Double symmetric: SC is in the COG
Open/single symmetric: SC is outside the structure
Crossing plates: SC is in the intersection between the plates
12
07/11/2012

Definition of bending shear stress:
D Vy S z Vz Sy = + b bI z bIy
We will make use of a coordinate system and In this coordinate system, with the centroid C as the origin (the neutral axis passes the centre of gravity):
the shear forces are called V and V, the static moments are called S and S and the moment area of inertia are called I and I.

This equation is equivalent with Eq. (3.24) in the compendium.
13
07/11/2012


If we require that the cross-section will not rotate for the loads that we apply the loads must pass through the shear centre
I.e. bending without twisting!
To determine the shear centre, we make use of the fact that the shear forces V and V must be statically equivalent to the shear stresses acting on the beam cross section This requirement determines the line of action for each of the shear forces V and V, which both pass though the shear center when there is no twist
14
07/11/2012


If the shear stresses xs are to be statically equivalent with the shear forces, their moment with regard to the x-axis or any longitudinal axis must be equal This gives the relation:
where 0 and 0 are the coordinates of the shear centre with regard to a provisional centre and h(s) is the moment arm for the shear flow

Insert Eq. (3.24) [ D =

b Vy Sz bIz + Vz Sy bIy
] into
This equation must hold for all values of the shear forces and it is only possible if and only if:
15
07/11/2012

And again, finally,
Bending shear and normal stress distributions in a transverse section.

Torsion-induced stresses
16
07/11/2012

Introduction to torsion
A catamaran in a sea-state which gives rise to torsion structural response.

An example of the structural response of a container vessel on the North Atlantic trade.
17
07/11/2012

A YouTube movie which shows a good example of the structural response of a container vessel in harsh weather (http://www.youtube.com/watch?feature=player_detailpage&v=qEkErF51Uxg)

Circular shaft in pure torsion
Noncircular shaft in pure torsion
18
07/11/2012


Warping displacement
Out-of-plane deformation during torsion loading

Circular cross-section: no warping Rectangular cross-section: very little warping Thin-walled and open I-shaped cross-section: large amount of warping

Cross-sections with and without warping
All but two cross-sections below show warping displacements behavior. However, most of the cross-sections (a, c and d) will produce very little warping.
19
07/11/2012


The analysis and understanding of the loading case is very important for following stress and strain analysis, see the example Case study:
y x z
A concentrated load, P, is acting on one of the flanges.

The structural response to this load, P, must be divided into the following load and stress/strain analyses:
Axial load, N Bending moment, My Bending moment, Mz Bimoment, B


Pure axial loading
Normal stress, A
Pure bending condition
Normal stress, B Shear stress, B
Superposition of stress components for various types of loading conditions. TOT = A + B + W TOT = B + SV + W
Pure St Venant torsion
Shear stress, SV
Vlasov torsion
Normal stress, W Shear stress, W

20
07/11/2012

St Venant torsion theory
Simple case study:
Circular tube with constant thin wall thickness, h. Subjected to a torque, Tx, which is constant over the length, L.
Of symmetric reasons, we will have constant shear stresses along the circumferential balancing the torque

St Venant torsion theory
An arbitrary element C of the tube wall, originally oriented along the generatrise, is transformed by shear deformation to a rhomb C with the shear angle In the figure we have that
r = L ( = Greek letter gamma) Hookes generalized law gives = G

Thus,
NOTE! This is one of the most perfect structures to be used for laboratory determination of the shear modulus.
21
07/11/2012

Kinematic relation
Geometric description of deformation in a continuum

Kinematic relation
Equations of the geometric description of deformation in a continuum: In the limit as x and y approaches zero we get:
22
07/11/2012

Constitutive relations

The constitutive relations are concerned with material dependence
I.e. relationships between stresses and strains.

If a material is elastic and isotropic, Hookes law can be applied
Isotropic: the material is assumed to have similar properties in all its directions.

Derivation
The graph from slide 13 with bending beam coordinates.
23
07/11/2012

Derivation

The cross-section will not change its shape, i.e. all strains in the yz-plane are zero Thus, z = y = yz = 0 The displacements of the crosssection can be described as a rigid body rotation of angle (x) around a centre of twist (VC)

Derivation
If the centre of twist has coordinates y0 and z0 we get expressions relating displacements in y- and z-direction to the rotation (x) according to the figure
Eq. (4.2)
v(x , y , z) = (x) (z z0 ) w(x , y , z) = (x) (y y0 )

24
07/11/2012

Derivation

We will have use for the displacement in the x-direction: u = u(x,y,z), Eq. (4.3) As we are dealing with torsion only (not bending), this function describes the warping displacements We will assume here that warping is not restrained anywhere in the beam This means that: x = 0, Eq. (4.4) In view of Eq. (4.1) and (4.4) it follows from Eq. (2.9) that: y = z = yz = x = 0, Eq. (4.5)

Derivation
Shear strains are given by Eq. (2.8) and we introduce Eq. (4.2) into that:
and the shear stresses are:
25
07/11/2012

Derivation
When there are no body forces (= forces from gravity or other inertia forces), the equilibrium from Eq. (2.6) gives:

Derivation
There are no restraints (free warping), and therefore, there are no strains in the longitudinal direction:
In combination with Eq. (4.7) we get:
26
07/11/2012

Derivation
The equilibrium conditions of Eqs (4.8b) and (4.8c) are only satisfied if:

Derivation

The displacement function u= f(y,z) is the basic unknown Insertion of Eq. (4.7) into Eq. (4.8a) gives us:
Introduce a stress function, (y,z), with the requirements that it is a function of y and z and twice differentiable and:
NOTE! The stress function is used here as a help to continue
27
07/11/2012

Derivation
Derivate once with regard to dy and dy, respectively:
Combine Eqs (4.14) and (4.7):

Derivation
Derivate!
Subtract!
28
07/11/2012

Derivation

Locate an arbitrary point, P, on the boundary of a solid cross-section Identify a tangential stress with components in the direction of the coordinate system

Derivation
Then,
The stress function, , must be zero along the boundary In all previous relations, this function only appeared as derivatives
Any constant would do = 0.

29
07/11/2012

Derivation

Derivation
By definition,
Combine with Eq. (4.14):
30
07/11/2012

Derivation
Note that in:
Hence, Eq. (4.18) can be rewritten:

Derivation
31
07/11/2012

Derivation

Using Eq. (4.19): we get that:
Since = 0 everywhere on the boundary, the value of the line integral on the previous slide is zero and:

Summary of derivation
The formulation of St Venant torsion theory is now complete and we can start to use it:
However, the solutions to the stress function with actual geometric boundaries are rather complex
This is why handbooks are full of pre-calculated torsional constants.
32
07/11/2012

Summary of derivation
Thin-walled open section:
(4.28)

Torsional constants and shear stress flow
33

Bending Induced Stresses

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Bending Induced Stresses

Uploaded by

Copyright:

Available Formats

07/11/2012

SHIPPING AND MARINE TECHNOLOGY

Professor Jonas Ringsberg p. 1

SHIPPING AND MARINE TECHNOLOGY

Professor Jonas Ringsberg p. 2

SHIPPING AND MARINE TECHNOLOGY

Repetition of bending-induced stresses

Professor Jonas Ringsberg p. 3

SHIPPING AND MARINE TECHNOLOGY

General requirements - validity of beam theory

Professor Jonas Ringsberg p. 4

SHIPPING AND MARINE TECHNOLOGY

General requirements - validity of beam theory

Therefore, the accuracy of the hull girder concept is very good.

Professor Jonas Ringsberg p. 5

SHIPPING AND MARINE TECHNOLOGY

Ideal theory vs. measurements

Professor Jonas Ringsberg p. 6

SHIPPING AND MARINE TECHNOLOGY

Example of stress distributions

Bending shear and normal stress distributions in a transverse section.

Professor Jonas Ringsberg p. 7

SHIPPING AND MARINE TECHNOLOGY

Requirements, bending beam theory

Professor Jonas Ringsberg p. 8

SHIPPING AND MARINE TECHNOLOGY

Bending normal stress

Professor Jonas Ringsberg p. 9

SHIPPING AND MARINE TECHNOLOGY

Example: bending with My 0 and Mz = 0 of a straight bar with rectangular cross-section

Professor Jonas Ringsberg p. 10

SHIPPING AND MARINE TECHNOLOGY

Pure bending in two directions

The strain in a point (y, z) in the cross-section at x is:

Professor Jonas Ringsberg p. 11

SHIPPING AND MARINE TECHNOLOGY

Pure bending in two directions

The integrals are:

Professor Jonas Ringsberg p. 12

SHIPPING AND MARINE TECHNOLOGY

Kinematic relation bending deformation

Professor Jonas Ringsberg p. 13

SHIPPING AND MARINE TECHNOLOGY

Pure bending in two directions

Normal strain and curvature can be derived as:

The stress in a point (y, z) in the cross-section at x is:

= E = E (0 + z y + y z) = ... = N My (zIz yIyz ) Mz (yIy zIyz ) + 2 A (Iy Iz Iyz )

Professor Jonas Ringsberg p. 14

SHIPPING AND MARINE TECHNOLOGY

Bending shear stress

Professor Jonas Ringsberg p. 15

SHIPPING AND MARINE TECHNOLOGY

Plane sections should remain plane after bending.

Professor Jonas Ringsberg p. 16

SHIPPING AND MARINE TECHNOLOGY

Sheared beam lamina of a homogenous beam

Equilibrium in the x-direction:

Professor Jonas Ringsberg p. 17

SHIPPING AND MARINE TECHNOLOGY

Sheared beam lamina of a homogenous beam

Professor Jonas Ringsberg p. 18

SHIPPING AND MARINE TECHNOLOGY

Bending shear stress

For thin-walled cross-sections holds: