RCI Project - Rail Component Subproject - 1 Bridge No.

DESIGN OF ABUTMENT WALLS

Specification data Unit Weight of Concrete Unit Weight of Soil Angle of Internal Friction () Co-eff., Active Earth Press. (Ca) Ultimate Strength of Steel (fy) Ultimate Strength of Conc. (f'c) Allowable Stress of Steel (fs) Allowable Stress of Concrete (fc) Shear Stress, no Web Reinf. (vc) Shear Stress (Punching) Allowable Bond Stress (d = Bar Diameter, mm) Modulus, Elasticity of Steel (Es) Modulus, Elasticity of Conc. (Ec) Cover + 1/2 the Bar Diameter For Above Unit Stresses, n For Above Unit Stresses, k For Above Unit Stresses, j For Above Unit Stresses, R

(Weep hole will not be used)

Cube Strength CF for Cylinder

35000

kn/m2 *

0.800

OR -->

= = = = = = 0.40 * fy = 0.40 * f'c = 2.89 * f'c^.5= 5.25 * f'c^.5= 113 * (f'c)^0.5/d = = 1103

25.00 18.00 30 0.50 5.00E+05 2.80.E+04 2.00E+05 1.1E+04 4.8E+02 878 1.90E+04
Kn/m (whichever is less)

= 2.00E+08 = 2.53E+07 = 91 = 7.90 = 0.307 = 0.898 = 1.54E+03

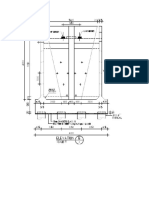
Rail Top Rail Ht. Sleeper Ballast W.C Design Data 8.919 0.172 0.220 0.300 0.080 Formation Level or Wall Top Level (Rail Level - Rail Ht. - Sleeper Thickness) Wall Bottom Slab Level Bottom of Bearing Level Assumptions Thickness of Abutment Wall at Top Thickness of Abutment Wall at Bottom Base Slab Thickness Assumed Width of the Abutment Wall Height from top of base, h Total Height of the Abutment, H 500 8.147 m //////////////// //////////////// mm

= = =

8.147 2.147 6.469

= = = = = =

500 1200 1800 9.200 6.00 7.80

6.00 m

EL 2.147

1200 1800 mm

ABUTMENT WALL SECTION (Typical)

DESIGN OF ABUTMENT WALLS DESIGN LOADS AND MOMENTS (per m length of wall) Static Earth Pressure in Abutment Wall, E AS = 1/2* *H 2 *C AS And acts at height from base of Abutment Wall, H/3 Corresponding Moment Dynamic Force Exerted by the Soil Mass, E AE = 1/2**H 2 *C AD And acts at height from base of Abutment Wall, H/2 Corresponding Moment Pressure due to Dead and Live Load Surcharge Active Earth Pressure, Rectangular Part, = (S+V)/L*Ca Acting at h/2 from section under consideration at base Active Earth Pressure, Triangular Part Acting at (h-((L-B)/3)) from section under consideration Corresponding Moment Longitudinal Forces on Abutment (With Fixed Bearing) Longitudinal Force, Coefficient = 0.50 84.00 Force per metre Width of Abutment And acts at the Bearing Level with Moment Arm Corresponding Moment DESIGN OF ABUTMENT WALLS DESIGN LOADS, MOMENTS AND SHEARS H = Height of Stem V = Shear at base of stem M = Moment at Base Slab Level MEMBER THICKNESS M = Design Moment R = Resisting Moment Coef. b = Unit Width of Member dr(Moment) dr(Shear) = V/(v*b) V = Design Shear v = Allowable Shear Stress of Concrete dr(Moment) > dr(Shear) Use dr = 804 mm Span : 25m Ton

= = = = = =

162.00 kn 2.00 m 324.00 kn-m 4.43 kn 3.00 m 13.28 kn-m

= = = = =

65.30 3.90 53.64 3.93 465.66

kn/m m kn/m m kn-m

= = = =

412 kn 44.76 kn/m width 4.32 m 193.44 kn-m

(As per UIC Code 774 - 3R, @nd edition, October 2001, Page 16, With CWR)

= = =

6.00 m 285.37 kn 996.38 kn-m

= 996.38 kn-m = 1.54E+03 kn/m = 1.00 m = 804 mm = 285.37 kn = 4.84E+02 kn/m = 590 mm

c = Coverage + 1/2 Dia.Reinforcement tr = dr + c= 804 + 91 ta = Actual Member Thickness Provided ta > tr Design is OK. HORIZONTAL SHRINKAGE REINFORCEMENT Ast = Required Area of Steel = K1 * ta * b OR = K1 * 380 * b (for ta <= 380 mm) (for ta > 380 mm)

= = =

91 mm 895 mm 1200 mm

Length of Member <= 9 m

Exposed Face 0.0025

Earth Length of Abutment Face ta = Actual Thickness of Memb 0.0020 b = Unit Width of Member

= = =

9.20 m 1200 mm 1.00 m

> 9m

0.0025

0.0020 * 380 * 1000 200 mm c/c (Ast * 380 * 1000 250 mm c/c (Ast = = = = 950 mm 1005 mm) 760 mm 804 mm)

Ast(Exposed Face) = 0.0025 Use 16 mm @ Ast(Earth Face) Use = 0.0020 16 mm @

VERTICAL EXPOSED FACE REINFORCEMENT Length of Member = Height of Returnwall (H + Ta) ta = Actual Thickness of Member K1 (Exposed Face) = 0.0025 Ast = Use 0.0025 * 16 mm @ 380 * 1000 200 mm c/c (Ast

= =

7.20 m < 9 m 1200 mm > 380 mm

= =

950 mm 1005 mm) <-----

VERTICAL EARTH FACE REINFORCEMENT Minimum Flexural Moment = [1.2 * Mcr =1.2 * 19.70 * f'c^0.5 * (b*h2/6)] Therefore, the Design Moment M = Design Moment fs = Allowable Flexural Strength of Steel j = Lever Arm Coef. da = Actual Effective Depth of Section = Actual Member Thickness - (Coverage + 1/2 Dia.Reinforcement) = ta - c= 1200 91 = 1109 mm 996.38 * 1.00E+09 Ast = --------------------------------------------------------------------------------- = 2.00E+05 * 0.898 * 1109 CHECK SHRINKAGE REINFORCEMENT Length of Member = Height of Wingwall (H + Ta) ta = Actual Thickness of Member K1 (Earth Face) = 0.0020 Ast = 0.0020 * Ast(Moment) > Ast(Shrinkage) Use 28 mm @ 380 * 1000 Use Ast 100 mm c/c (Ast

= 949.37 = 996.38 = 996.38 = 2.00E+05 = 0.898

kn-m kn-m kn-m kn/m

5004 mm

= =

7.20 m < 9 m 1200 mm > 380 mm

= = =

760 mm 5004 mm 6158 mm)

CHECK BOND bs(allow) = Allow. Bond Stress = 483.59 * (fc')^0.5/d OR = 1103 kn/m (whichever is less) d = Bar Dia. bs(allow) = = 28 mm

1.90E+04 /d kn/m

1.90E+04 / 28 = 677.69 kn/m < 1103 kn/m Use bs(allow) = 677.69 kn/m V bs(actual) = Actual Bond Stress = -----------------------------------tp * j * da V = Design Shear = 285.37 kn tp = Total Perimeter of Steel Bars = 3.14*Diameter Bars / Spacing

880 mm

285.37 * 1.00E+06 bs(actual) = ------------------------------------------------------------------------------------------------------= 325.84 kn/m 880 * 0.898 * 1109

The allowable bond stress is compared to the actual bond stress to determine whether the design is adequate. bs(allow) > bs(actual) Design is OK. <----BAR CURTAILMENT LOCATION OF 1ST BAR CURTAILMENT M(resisting) = Resisting Moment = (1/2 Ast) * fs * j * da 1/2 Ast = Area of Steel available after Bar Curtailment fs = Allowable Flexural Strength of Steel j = Lever Arm Coef. da = Actual Effective Depth of Section where curtailment occurs = Tt + (Tb - Tt) * h /H - c = 409 + 116.67 * h (h = Distance from Top of Wingwall (m)) At the location where the bars can be curtailed M(resisting) = M(actual). M(resisting) = 226.10 M(actual) = By trial and error, it is found that h + 64.49 *h = = = 520.84 kn-m 519.96 kn-m 4.57 m

= 3079 mm = 2.00E+05 kn/m = 0.898

x = Distance from Base Slab Level to Location of the 1st Bar Curtailment = H - h + dx H = Height of Wing Wall = 6.00 m dx = Extra Distance to extend the Bars beyond the theoretical Curtailment Location = da OR = 12 * Bar Diameter (whichever value is larger) da = Actual Effective Depth of Section where curtailment occurs = 409 + 116.67 *h = 942 mm 12 * Bar Diameter = 12 * 28 = 336 mm da > 12 * Bar Diameter Use dx = = 942 mm <----x = 6.00 4.57 + 0.942 = 2.37 m If the location of curtailment is less than 1 m from the top of the returnwall no curtailment is made. H-x = 3.63 > 1 m Curtailment should be made. CHECK SHRINKAGE REINFORCEMENT Ast(Moment) = 1/2 * Ast(Moment, at Base Slab Level Section) = 1/2 * 5004 = Ast(Shrinkage) = 760 mm Ast(Moment) > Ast(Shrinkage) Use x =

2502 mm 2.37 m <-----

LOCATION OF 2ND BAR CURTAILMENT M(resisting) = Resisting Moment = (1/4 Ast) * fs * j * da 1/4 Ast = Area of Steel available after bar curtailment = fs = Allowable Flexural Strength of Steel = j = Lever Arm Coef. = 0.898 da = Actual Effective Depth of Section where curtailment occurs = Tt + (Tb - Tt) * h /H - c = 409 + 89.74 *h M(resisting) = 113.05 + 24.81 *h = M(actual) = = By trial and error, it is found that h = x = Distance from Base Slab Level to Location of the 2nd Bar Curtailment = H - h + dx H = Height of R.wall = 6.00 dx = Extra Distance to extend the Bars beyond the theoretical Curtailment Location = da OR = 12 * Bar Diameter (whichever value is larger) da = 409 + 89.74 *h = 658 12 * Bar Diameter = 12 * 28 = 336

1539 mm 2.00E+05 kn/m

181.76 kn-m 181.99 kn-m 2.77 m

mm mm

da > 12 * Bar Diameter Use dx = 658 mm <----x = 6.00 2.77 + 0.66 = 3.89 m If the location of curtailment is less than 1 m from the top of the returnwall no curtailment is made. H-x = 2.11 > 1 m Curtailment should be made. CHECK SHRINKAGE REINFORCEMENT Ast(Moment) = 1/4 * Ast(Moment, at Apron Level Section) = 1/4 * 5004 = 1251 mm Ast(Shrinkage) = 760 mm Ast(Moment) > Ast(Shrinkage) Use x = 3.89 m <----DESIGN OF ABUTMENT BACK WALL Formation Level or Wall Top Level Bottom of Bearing Level Height of the Back wall Unit Weight of Soil Static Component of Earth Pressure Coefficient, CAS While Dynamic Component of Earth Pressure Coefficient CAD Static Condition Static Earth Pressure in Abutment, E AS = 1/2* *H 2 *C AS (Submerged) Static Earth Pressure in Abutment, E AS = 1/2* w *H 2 *C AS(Water) And acts at height from base of Abutment, H/3 Corresponding Moment Dynamic Condition Dynamic Force Exerted by the Soil Mass, E AE = 1/2**H 2 *C AD And acts at height from base of Abutment, H/2 Corresponding Moment Pressure due to Dead and Live Load Surcharge Active Earth Pressure, Rectangular Part, = (S+V)/L*Ca Acting at h/2 from section under consideration at base Active Earth Pressure, Triangular Part Acting at (h-((L-B)/3)) from section under consideration Corresponding Moment DESIGN LOADS, MOMENTS AND SHEARS H = Height of Stem V = Shear at base of stem M = Moment at Base Slab Level MEMBER THICKNESS M = Design Moment R = Resisting Moment Coef. b = Unit Width of Member dr(Moment) dr(Shear) = V/(v*b) V = Design Shear v = Allowable Shear Stress of Concrete dr(Moment) < dr(Shear) Use dr = 169 mm = = = 91 mm 260 mm 500 mm

= = = = = = = = = = = = = = = = = =

8.147 6.469 1.678 18.00 0.500 0.014 5.63 14.08 0.56 11.02

m m m kn/m3 **

Kn/m Kn/m m kn-m

0.35 Kn/m 0.84 m 0.29 kn-m 12.76 0.84 48.71 0.39 29.64 kn/m m kn/m m kn-m

= = =

1.678 m 81.52 kn 40.95 kn-m

= 40.95 kn-m = 1.54E+03 kn/m = 1.00 m = 163 mm = 81.52 kn = 4.84E+02 kn/m = 169 mm

c = Coverage + 1/2 Dia.Reinforcement tr = dr + c= 169 + 91 ta = Actual Member Thickness Provided ta > tr Design is OK.

HORIZONTAL SHRINKAGE REINFORCEMENT Ast = Required Area of Steel = K1 * ta * b OR = K1 * 380 * b (for ta <= 380 mm) (for ta > 380 mm) Length of Member <= 9 m > 9m Exposed Face 0.0025 0.0025 Earth Length of Abutment Face ta = Actual Thickness of Memb 0.0020 b = Unit Width of Member 0.0020 * 380 * 1000 200 mm c/c (Ast * 380 * 1000 250 mm c/c (Ast = = = 0.00 m 500 mm 1.00 m

Ast(Exposed Face) = 0.0025 Use 16 mm @ Ast(Earth Face) Use = 0.0020 16 mm @

= = = =

950 mm 1005 mm) 760 mm 804 mm)

VERTICAL EXPOSED FACE REINFORCEMENT Length of Member = Height of Returnwall (H + Ta) ta = Actual Thickness of Member K1 (Exposed Face) = 0.0025 Ast = Use 0.0025 * 16 mm @ 380 * 1000 200 mm c/c (Ast

= =

1.68 m < 9 m 500 mm > 380 mm

= =

950 mm 1005 mm) <-----

VERTICAL EARTH FACE REINFORCEMENT Minimum Flexural Moment = [1.2 * Mcr =1.2 * 19.70 * f'c^0.5 * (b*h2/6)] Therefore, the Design Moment M = Design Moment fs = Allowable Flexural Strength of Steel j = Lever Arm Coef. da = Actual Effective Depth of Section = Actual Member Thickness - (Coverage + 1/2 Dia.Reinforcement) = ta - c= 500 91 = 409 mm 164.82 * 1.00E+09 Ast = -------------------------------------------------------------------------------- = 2.00E+05 * 0.898 * 409 CHECK SHRINKAGE REINFORCEMENT Length of Member = Height of Wingwall (H + Ta) ta = Actual Thickness of Member K1 (Earth Face) = 0.0020 Ast = 0.0020 * Ast(Moment) > Ast(Shrinkage) Use 25 mm @ 380 * 1000 Use Ast 200 mm c/c (Ast

= 164.82 = 164.82 = 164.82 = 2.00E+05 = 0.898

kn-m kn-m kn-m kn/m

2244 mm

= =

1.68 m < 9 m 500 mm > 380 mm

= = =

760 mm 2244 mm 2454 mm)

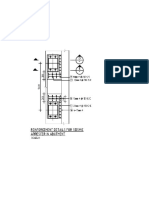
REINFORCEMENTS Member Reinforcement in Directions and at Top and Bottom Ver exp face Ver earth face Hor exp face Hor earth face Ver exp face Ver earth face Hor exp face Hor earth face Ast required moment shrink (mm) (mm) 950 5004 760 950 760 950 2244 760 950 760 Bar dia (mm) 16 28 16 16 16 25 16 16 Spacing @ (mm c/c) 200 100 200 250 200 200 200 250 Ast provided (mm) 1005 6158 1005 804 1005 2454 1005 804

STEM

BACK WALL

BAR CURTAILMENTS Curt. ht. Member Curtailment from top No. h (m) STEM 1st curtailment 4.57 2nd curtailment2.77 MEMBER THICKNESS Member Moment (kn-m) 996.38 Shear (kn) 285.37 Member thickness Required Provided dr(mom) dr(shear) tr(req) ta(act) (mm) (mm) (mm) (mm) 804 590 895 1200 Depth of sectn.at curt.pt. da (mm) 942 658 12 * (mm) 336 336 Curt. pt. above bot slab, x (m) 2.37 3.89 Ast momt. (mm) 2502 1251 Ast shrink (mm) 760 760

STEM