Eur ope a n J our nal of Oper at i onal Res ear ch 48 (1990) 9 - 2 6 9

Nor t h- Hol l a nd
How to make a decision:
The Analytic Hierarchy Process
Thomas L. Saaty
Joseph M. Katz Graduate School of Business, University of Pittsburgh, Pittsburgh, PA 15260, USA
Abstract: Thi s paper serves as an i nt r oduct i on to the Anal yt i c Hi er ar chy Process - A mul t i cri t eri a decision
maki ng appr oach in which fact ors are arranged in a hi erarchi c structure. The pri nci pl es and the phi l osophy
of the t heory are summari zed giving general backgr ound i nf or mat i on of the t ype of measur ement utilized,
its propert i es and applications.
Keywords : Decision, pri ori t y, rank, cost - benef i t , scales, ratios
1. Ho w t o s t ruct ure a de c i s i o n pr obl e m
Perhaps the most creative task in maki ng a
decision is to choose t he fact ors t hat are i mpor t ant
for t hat decision. In the Anal yt i c Hi er ar chy Proc-
ess we arrange these factors, once selected, in a
hierarchic st ruct ure descendi ng f r om an overall
goal to criteria, subcriteria and alternatives in
successive levels.
To a person unfami l i ar with the subject t here
may be some concer n about what to i ncl ude and
where to include it. When const ruct i ng hierarchies
one must i ncl ude enough rel evant detail to:
represent the pr obl em as t hor oughl y as possi-
ble, but not so t hor oughl y as to lose sensitivity to
change in t he elements;
consi der the envi r onment surroundi ng the
probl em;
i dent i fy the issues or at t ri but es t hat cont r i but e
to the solution; and
i dent i fy the part i ci pant s associated with the
probl em.
Arrangi ng the goals, at t ri but es, issues, and stake-
hol ders in a hi erarchy serves two purposes. It
provi des an overall view of the compl ex relation-
ships i nherent in the situation; and helps the deci-
sion maker assess whet her the issues in each level
are of the same or der of magni t ude, so he can
compar e such homogeneous el ement s accurately.
Recei ved Nove mbe r 1989
One cert ai nl y cannot compar e accordi ng to size a
foot bal l with Mr. Everest and have any hope of
getting a meani ngful answer. The foot bal l and Mt.
Everest must be compar ed in sets of objects of
their class. Lat er we give a f undament al scale of
use in maki ng the compari son. It consists of verbal
j udgment s ranging from equal t o ext reme (equal,
moder at el y more, st rongl y more, very st rongl y
more, ext remel y more) correspondi ng to the verbal
j udgment s are the numeri cal j udgment s (1, 3, 5, 7,
9) and compromi ses bet ween these values. We
have compl et ed compi l i ng a di ct i onar y of hier-
archies pert ai ni ng to all sorts of probl ems, f r om
personal to cor por at e to public.
A hi erarchy does not need to be compl et e, that
is, an el ement in a given level does not have to
funct i on as an at t r i but e (or cri t eri on) for all the
elements in t he level below. A hi erarchy is not the
t radi t i onal decision tree. Each level may represent
a di fferent cut at the probl em. One level may
represent social fact ors and anot her political fac-
t or to be eval uat ed in t erms of t he social fact ors or
vice versa. Furt her, a decision maker can insert or
el i mi nat e levels and el ement s as necessary to
cl ari fy the task of setting priorities or to sharpen
the focus on one or mor e part s of the system.
El ement s t hat have a global charact er can be
represent ed at the hi gher levels of the hi erarchy,
ot hers t hat specifically charact eri ze t he pr obl em at
hand can be devel oped in great er dept h. The task
of setting priorities requires t hat the criteria, the
0377- 2217/ 90/ $03. 50 1990 - El sevi er Sci ence Publ i s her s B.V. ( Nor t h- Hol l a nd)
10 T.L. Saaty / The AHP: How to make a decision
propert i es or features of the alternatives bei ng
compared, and t he alternatives themselves are
gradual l y l ayered in the hi erarchy so t hat it is
meani ngful to compar e t hem among themselves in
rel at i on to the elements of the next hi gher level.
Finally, aft er j udgment s have been made on t he
i mpact of all the elements and priorities have been
comput ed for the hi erarchy as a whole, sometimes,
and with care, the less i mpor t ant elements can be
dr opped f r om furt her consi derat i on because of
t hei r relatively small i mpact on the overall objec-
tive. The priorities can t hen be r ecomput ed
t hroughout , ei t her with or wi t hout changi ng the
remai ni ng j udgment s.
2. Sc a l e s o f m e a s u r e m e n t - Avoi di ng me r e num-
ber c r unc hi ng
One might argue t he whole process of decision
maki ng is so unst r uct ur ed and so amor phous t hat
it is no use t ryi ng to be precise. One is t hen
t empt ed t o go f ur t her and concl ude t hat " par -
t i ci pant sat i sfact i on" is the mai n obj ect i ve of deci-
sion making. Were this the case, t hen mul t i cri t eri a
decision maki ng woul d be a simple mat t er of
using ingenuity, suppor t ed wi t h mat hemat i cal
t ermi nol ogy, to i mpr ove number s t hat please peo-
ple. But di fferent sets of ar bi t r ar y number s are
likely to result, pr oduci ng di fferent decisions, and
we are right back where we started. One set of
number s pleases a group of peopl e who mi ght be
equal l y pl eased wi t h anot her set of number s t hat
cont radi ct s the r ecommendat i ons of t he first set.
Thi s is mere number crunching. If a decision
suppor t t heory is to be t rust wort hy t here must be
uni queness in the represent at i on of j udgment s, the
scales deri ved f r om these j udgment s, and the scales
synthesized f r om the deri ved scales.
Let us consi der for a moment group i nt er act i on
t hat oft en leads t o cert ai n expect at i ons, somet i mes
arising f r om the very heat of t he debat e. Such a
debat e cannot always i ncor por at e in its argument s
t he refi nement s resulting f r om t he mat hemat i cal
t radeoffs to ensure drawi ng valid conclusions.
Somet i mes part i ci pant s accept a process and its
out come because the si t uat i on is so compl ex and
t he argument s so convol ut ed t hat what ever
surfaces in t he end appears plausible. Al t hough
convi nci ng a group about its qual i t at i ve prefer-
ences involves the politics of persuasi on and of
wheeling and dealing, it is essential t hat t he deci-
sion t heory itself used to assist the group in arriv-
ing at a decision be i nvari ant to politics and
behavi or. It shoul d be a science of scaling based
on mat hemat i cs, phi l osophy and psychol ogy.
Among t he vari ous number crunchi ng prac-
tices, the most obj ect i onabl e one is to assign any
set of number s to j udgment s on alternatives under
a part i cul ar criterion, and t hen normal i ze these
number s ( by mul t i pl yi ng t hem by a const ant that
is the reci procal of t hei r sum). General l y, di fferent
sets of number s are used to scale the j udgment s
for the al t ernat i ves under di fferent criteria. All the
new normal i zed sets now lie in the i nt erval [0, 1],
no mat t er what scale t hey originally came from,
and can be passed of f t o the uni ni t i at ed as com-
parabl e. The appeal i ng par t of this pract i ce is t hat
t he number s have an appar ent l y uni f or m underl y-
ing st ruct ure and l ook not unlike probabilities.
Thus t hey go unchal l enged by t he decision maker
and are t hen mani pul at ed by t he consul t ant or
faci l i t at or who weights and adds t hem to find the
most pr ef er r ed alternative.
Not e t hat when t he initial number s assigned
bef or e nor mal i zat i on are ordinals, ar bi t r ar y num-
bers t hat preserve or der but carry no i nf or mat i on
about di fferences or rat i os of relative magni t udes,
the resul t i ng t r ansf or mat i on produces a new set of
ordi nal s lying bet ween zero and one and you can
be sure onl y t hat it preserves the same order. The
operat i ons of weighting and addi ng cannot t hen
be meani ngful because it is very likely t hat differ-
ent results will be pr oduced for di fferent choices
of the ordi nal numbers. By a j udi ci ous choi ce of
ordi nal s one can make an al t ernat i ve t hat is domi -
nant on even one cri t eri on, no mat t er how uni m-
por t ant t hat cri t eri on may be, have t he largest
val ue aft er weighting and addi ng and thus t urn
out to be t he most preferred. Any met hod such as
this is not a deci si on t heor y but an appr oach t hat
can mislead peopl e.
The Anal yt i c Hi er ar chy Process is rigorously
concer ned with t he scaling pr obl em and what sort
of number s to use, and how to correct l y combi ne
t he pri ori t i es resulting f r om them. A scale of
measur ement consists of t hree elements: A set of
objects, a set of numbers, and a mappi ng of the
obj ect s to t he numbers. In a st andar d scale a unit
is used to const r uct t he rest of the number s of the
scale. Exampl es of such a uni t are the inch, the
pound, t he angst rom, and the dollar. A st andar d
T.L. Saaty / The AHP: How to make a decision 11
scale can be used to measur e obj ect or event s wi t h
respect to the pr oper t y for whi ch a scale is design-
ed to measure. Since the uni t is ar bi t r ar y, one can
have di fferent number s to whi ch the obj ect s are
mapped. Because a st andar d scale is not unique, it
is i mpor t ant to i nt er pr et the meani ng of the num-
bers used in the scale. Thus, in general, the num-
bers obt ai ned f r om such a scale are merel y stimuli
for the memor y (what it felt like the l ast t i me the
t emper at ur e was - 1 5 C) and have no i nt ri nsi c
significance. However, most careful l y desi gned
st andar d scales are hel pful in t hat t hey preserve
cert ai n numeri cal rel at i ons in the measur ement s
(t he mappi ng) of the objects, giving us a bet t er
way to i nt erpret the stimuli t hey are measur i ng
t han ar bi t r ar y scales.
A scale may or may not have zero for an origin.
For exampl e, a scale of ordi nal number s can begi n
wi t h any number . A rat i o scale, such as absol ut e
t emper at ur e preserves origin. I nt er val scales, whi ch
measur e the same phenomena like t emper at ur e,
preserve l i near relations, but ma y have di fferent
origins. Zer o on t he Fahr enhei t scale is a di fferent
t emper at ur e t han zero on the Celsius scale. Bot h
are i nt erval scales. Agai n, the number s on these
scales mean not hi ng unless one can recall si t ua-
tions associ at ed wi t h the numer i cal readi ngs bei ng
consi dered. They are j ust a conveni ent means of
communi cat i ng charact eri st i cs of obj ect s or situa-
tions wi t hout ever ybody havi ng to experi ence
t hem.
It oft en happens t hat the i nt er pr et at i ons of
numer i cal stimuli f r om a given st andar d scale
di ffer dependi ng on the ci rcumst ances. Ther e is no
si mpl e rule t hat can be appl i ed to i nt er pr et read-
ings f r om even a single scale when it is appl i ed to
a nat ural phenomenon. I nt ensi t y of sun light has a
di fferent significance for di fferent purposes. I t
may be useful for sunbat hi ng, but t oo bri ght for
reading. Similarly, a monot oni c rel at i on bet ween
successive readi ngs f r om a st andar d scale do not
assure us t hat even hi gher readi ngs will be bet t er
(or worse). Mor e (or less) t emper at ur e does not
necessari l y cor r espond to mor e (or less) useful-
ness. Low t emper at ur es are uncomf or t abl e. As the
readi ngs rise, t hey become mor e comf or t abl e and
as t hey rise hi gher t hey can agai n become uncom-
fort abl e. On the ot her hand, to preserve some
foods, low t emper at ur es are very desi rabl e and as
t he readi ngs rise, t hey become undesi rabl e, and as
t hey rise still hi gher t hey coul d become desi rabl e
again. Our val ues of comf or t and desi rabi l i t y and
ot her social effect s have to be at the bot t om of
every i nt er pr et at i on and depend on hi gher goals
t hat we ma y have in mi nd.
For a large numbe r of scales used in physics, it
is i mpl i ci t l y assumed t hat the scale can be ex-
t ended out to i nfi ni t y and appl i ed to every i magi n-
abl e ci rcumst ance. I n ot her words, i nt er pr et at i on
in physi cs assumes event s as homogeneous, no
mat t er how near or far f r om the origin t hey may
fall. What is mos t ast oni shi ng is the assumpt i on in
physi cs t hat obj ect s yet unknown but with the
same di mensi onal charact eri st i cs of the known
obj ect s bei ng measur ed can in fact be measur ed in
the same way. Real i zat i on of the di fferent i nt er-
pr et at i ons we can make of the same number in
physi cs woul d i ndi cat e t hat when number s fall
out si de the r eal m of experi ence it is logical to
suspend the ext ensi on of the t rut h we const r uct
f r om experi ence to a domai n for which we have no
knowl edge and feeling. It woul d be most l y fictive
specul at i on.
In economi cs, the ar i t hmet i c val ue of a dol l ar is
assumed to be the same no mat t er whet her a
per son has onl y one or a mi l l i on dollars. But in
real i t y it is not. To buy a new Mercedes, t en
dol l ars and one hundr ed dol l ars are nearl y equal l y
i nadequat e or useless as down payment s. On the
ot her hand, for buyi ng groceries, a hundr ed dol-
lars is much mor e useful, pract i cal l y ten t i mes
mor e useful t han ten dollars. The first t housand
dol l ars ear ned is much mor e i mpor t ant t han the
first t housand dol l ars ear ned af t er a million.
We must be const ant l y and careful l y at t ent i ve
to how we i nt er pr et dat a f r om scales. St andar d
scales force on us a way of t hi nki ng t hat is not in
compl et e ha r mony wi t h the way we real l y feel
about what t hey are measuri ng.
Ther e is a mor e general met hod of measure-
ment t hat does not make use of st andar d scales. It
is the met hod of rel at i ve meas ur ement s useful for
pr oper t i es for whi ch t here is no st andar d scale of
meas ur ement (love, pol i t i cal clouL straightness).
These are known as i nt angi bl e propert i es. The
numbe r of such pr oper t i es is ext r emel y large. We
can scarcel y hope to device st andar d scales for
t hem all. We are dri ven to rel at i ve scales, and a
surpri si ng t hi ng is t hat t hey can serve as a st and-
ard for how to handl e t he very few st andar d scales
we have, and not the ot her way round. A r emar ka-
bl e aspect of rel at i ve scales is t hat t hey can use
12 T . L Saaty / The AHP: How to make a decision
i nf or mat i on f r om st andar d scales when t here is a
par t i cul ar need to do so. Measur ement s in a
st andar d rat i o scale are t r ansf or med to meas-
ur ement s in a rel at i ve r at i o scale by nor mal i zi ng
t hem.
Thi s conver si on process gives us a hi nt about
t he di fference bet ween the t wo ki nds of scales. A
rel at i ve scale for a pr oper t y is gener at ed f or a
specific set of entities or objects. A st andar d scale
for a pr oper t y is al ways out t here r eady t o be
cal l ed i nt o use. Mor e significantly, a rel at i ve scale
is essential to r epr esent pri ori t y or i mpor t ance if
one is generat i ng the scale by maki ng di rect ob-
servat i ons and j udgment s about t he pr oper t y un-
der study. I t is also useful when one is i nt er pr et i ng
what the dat a f r om a st andar d scale real l y signify.
Rel at i ve scales are al ways needed t o r epr esent
subj ect i ve underst andi ng. Mor e is said about
ar i t hmet i c rel at i ons bet ween the t wo t ypes of scales
in Sections 8 and 12.
3. Pai red c o mpa r i s o ns a s rat i os
When we measur e somet hi ng wi t h respect to a
pr oper t y, we usual l y use some known scale for
t hat purpose. A basi c cont r i but i on t o t he subj ect
of this paper , t he Anal yt i c Hi er ar chy Process
( AHP) is how to deri ve rel at i ve scales usi ng j udg-
ment or dat a f r om a st andar d scale, and how to
per f or m the subsequent ar i t hmet i c oper at i on on
such scales avoi di ng useless numbe r crunchi ng.
The j udgment s are gi ven in t he f or m of pai r ed
compar i sons [6,7,8] One of t he uses of a hi er ar chy
is t hat it allows us to focus j udgment separ at el y on
each of several pr oper t i es essent i al f or maki ng a
sound decision The mos t effect i ve way to con-
cent rat e j udgement is to t ake a pai r of el ement s
and compar e t hem on a single pr oper t y wi t hout
concer n for ot her pr oper t i es or ot her el ement s.
Thi s is why pai r ed compar i sons in combi nat i on
wi t h the hi erarchi cal st ruct ure are so useful in
deri vi ng measur ement . We also not e t hat some-
t i mes compar i sons are made on t he basi s of st and-
ards est abl i shed in me mor y t hr ough experi ence or
training.
Assume t hat we are gi ven n stones, At , . . . , An,
whose weights w I . . . . . w,, respect i vel y, are known
to us. Let us f or m the mat r i x of pai rwi se rat i os
whose rows give the rat i os of the weights of each
st one with respect to all others. Her e t he smal l er
A 1
AI wl / w~
A2 w2 / wl
A , w n / w 1
{Wwl
W2
~- n
of each pai r of st ones is used as t he unit, and the
l arger one is measur ed in t er ms of mul t i pl es of
t hat unit. I t is di ffi cul t to do t he i nverse compar i -
son wi t hout agai n usi ng t he smal l er st one as the
unit. Thi s is a sort of bi as in human t hi nki ng,
whi ch l eads t o consi der i ng a nons ymmet r i cal out -
come and t he i ncl i nat i on not to force s ymmet r y
on it. We have t he mat r i x equat i on:
A 2 . . . A n
wl / w2 " " Wl/W. I
W 1
I
W a/W 2 . . . w j w o l w?
w. / w2 . . . w. / wn ] w.
The f or egoi ng f or mul at i on has t he advant age of
giving us t he solution But it also gives rise to a far
reachi ng t heoret i cal i nt er pr et at i on. We have mul t i -
pl i ed A on the ri ght by t he vect or of wei ght s
w = ( %, w 2 . . . . . wn) x. The resul t of this mul t i pl i -
cat i on is nw. I f n is an ei genval ue of A, t hen w is
the ei genvect or associ at ed wi t h it. Now A has r ank
one because every row is a const ant mul t i pl e of
t he first row. Thus all its ei genval ues except one
are zero. The sum of t he ei genval ues of a mat r i x is
equal to its trace, t he sum of t he di agonal ele-
ment s, and in this case, the t race of A is equal to
n. Ther ef or e, n is t he largest, or pri nci pal , eigen-
val ue of A.
The sol ut i on of A w = nw, called t he pr i nci pal
right ei genvect or of A, consi st s of posi t i ve entries
and is uni que to wi t hi n a mul t i pl i cat i ve const ant .
To make w uni que, we nor mal i ze its ent ri es by
di vi di ng by t hei r sum. I t is clear t hat if we are
gi ven t he compar i s on mat r i x A, we can recover
t he scale. I n this case t he sol ut i on is the nor mal -
ized versi on of any col umn of A.
The mat r i x A =( a i j ) , a i j =w i / w j , i, j =
1 . . . . . n, has posi t i ve ent ri es everywhere and satis-
fies the r eci pr ocal pr oper t y aj i = 1 / a i j . Any ma-
trix wi t h t hi s pr oper t y is called a reci procal ma-
trix. I n addi t i on, A is cons i s t ent because the fol-
l owi ng condi t i on is satisfied:
aj ~ = a i k / a i j , i , j , k = 1 . . . . . n. (1)
T.L. Saaty / The AHP: How to make a decision 13
We see t hat the ent i re mat r i x can be const r uct ed
f r om a set of n el ement s whi ch f or m a chai n (or
mor e generally, a spanni ng tree, in gr aph- t heor et i c
t ermi nol ogy) across the rows and col umns.
I t is easy to pr ove t hat a consi st ent mat r i x must
have the r at i o f or m A = ( wJ wj ) , i, j = 1 . . . . . n. A
necessary condi t i on for consi st ency is t hat A be
reci procal . We show bel ow t hat a necessary and
sufficient condi t i on for consi st ency is t hat the
pr i nci pal ei genval ue of A be equal to n, the or der
of A. When A is i nconsi st ent , these t wo observa-
t i ons serve to hel p us derive a rat i o scale whose
rat i os are close to t hose of an under l yi ng scale
w -- (w I . . . . . w,). The reci procal axi om of the AHP
ensures t hat per t ur bat i ons of a rat i o scale are
t hemsel ves reci procal . The homogenei t y axi om en-
sures for the i nconsi st ent case t hat the per t ur ba-
t i ons woul d be small, and hence t hat the t wo
pri nci pal ei genval ues are close, f r om whi ch it
woul d follow by an ar gument gi ven in [14, p. 671
t hat the deri ved scale is close to an underl yi ng
rat i o scale. I n addi t i on, this second axi om enabl es
us to expl ore the i mpr ovement of some of the
j udgment s, thus al so t he i mpr ovement of i ncon-
si st ency and the scale appr oxi mat i on. But t here
still r emai ns the quest i on of order preservat i on.
The met hod we use to deri ve the scale must not
onl y yield a rat i o scale, but also capt ur e the or der
i nherent in the j udgment s, a very st rong requi re-
ment indeed.
I n a general deci si on- maki ng envi r onment , we
cannot give the preci se val ues of the w , / w ) but
onl y est i mat es of t hem. Let us consi der est i mat es
of these values given by an expert who may make
smal l errors in j udgment . I t is known f r om eigen-
val ue t heory [14], t hat a small per t ur bat i on ar ound
a si mpl e eigenvalue, as we have in n when A is
consi st ent , leads to an ei genval ue pr obl em of the
f or m Aw=)tmaxW where Xma x is the pr i nci pal
ei genval ue of A where A may no l onger be con-
sistent but is still reci procal . The pr obl em now is:
to what ext ent does w reflect t he exper t ' s act ual
opi ni on? Not e t hat if we obt ai n w by solving this
pr obl em, and t hen f or m a mat r i x wi t h the ent ri es
( w , / w j ) , we obt ai n an appr oxi mat i on to A by a
consi st ent mat ri x.
We now show the interesting, and per haps
surpri si ng result t hat i nconsi st ency t hr oughout
t he mat r i x can be capt ur ed by a single numbe r
X m~x- n, whi ch measur es the devi at i on of the
j udgment s f r om t he consi st ent appr oxi mat i on.
Let a , j = ( 1 + 6 ~ j ) w J ~ * ) , 6~j> - 1 , be a per-
t ur bat i on of w y w j , where w is the pr i nci pal eigen-
vect or of A.
T h e o r e m 1. Xmax > / g/"
Pr o o f : Usi ng aj, = 1 / a j i , and A w - - X . . . . w, we
have
I a , 2
- = - ~ l + 6 , j >~0" [] ( 2 )
~max n n l ~ i < j ~ n
Theor em 2. A i s c o n s i s t e n t i f a n d o n l y i f )~ m a x = ?Z.
Proof. I f A is consi st ent , t hen because of (1), each
row of A is a const ant mul t i pl e of a given row.
Thi s i mpl i es t hat the r ank of A is one, and all but
one of its ei genval ues Xi, i = 1, 2 . . . . . n, are zero.
However , it follows f r om our earlier ar gument t hat
F~= iX, = Tr ace( A) = n. Therefore, X m a x = n. Col3-
versely, Xm, x = n i mpl i es 6 , j = 0, and a~j = w y w j .
[]
For the consi st ency i ndex (CI), we adopt the
val ue (ki n, X - n ) / ( n - 1). It is the negat i ve aver-
age of the ot her r oot s of the charact eri st i c pol y-
nomi al of A. Thi s val ue is compar ed wi t h the
same i ndex obt ai ned as an average over a large
number of r eci pr ocal mat r i ces of the same order
whose ent ri es are r andom. I f the rat i o (called the
consi st ency rat i o CR) of CI to t hat f r om r a ndom
mat ri ces is si gni fi cant l y smal l (careful l y speci fi ed
to be about 10% or less), we accept the est i mat e of
w. Ot herwi se, we at t empt to i mpr ove consi st ency.
The r eader may know about the exper i ment al
fi ndi ngs of t he psychol ogi st Geor ge Miller in the
1950' s [4]. He f ound t hat in general, peopl e (such
as chess expert s) coul d deal wi t h i nf or mat i on in-
vol vi ng si mul t aneousl y onl y a few facts, seven plus
or mi nus two, he wrot e. Wi t h more, they become
conf used and cannot handl e the i nf or mat i on. Thi s
is in ha r mony wi t h the st abi l i t y of the pr i nci pal
ei genval ue to small per t ur bat i ons when n is small
[7,14], and its cent ral rol e in the meas ur ement of
consi st ency.
Vargas [12] st udi ed the case where the coeffi-
ci ent s of the mat r i x are r a ndom variables. He
focused his at t ent i on on g a mma di st r i but ed coeffi-
ci ent s and deri ved a Di ri chl et di st ri but i on for the
component s of the ei genvect or when the mat r i x is
14 T.L. Saaty / The AHP: How to make a decision
consistent. When the matrix is inconsistent, the
10% consistency bound is a sufficient measure to
ensure that the eigenvector follows the Dirichiet
distribution with given parameters which can be
computed from the corresponding consistent ma-
trix. The gamma assumption is a powerful one
because of the inherent density of linear combina-
tions of these distributions.
4. Two examples
The AHP is used with two types of measure-
ment, relative and absolute, the latter having to do
with memory standards mentioned above. In both,
paired comparisons are performed to derive prior-
ities for criteria with respect to the goal. In rela-
tive measurement, paired comparisons are per-
formed throughout the hierarchy including on the
alternatives in the lowest level of the hierarchy
with respect to the criteria in the level above. In
absolute measurement, paired comparisons are
also performed through the hierarchy with the
exceptions of the alternatives themselves. The level
just above the alternatives consists of intensities or
grades which are refinements of the criteria or
subcriteria governing the alternatives. One pair-
wise compares the grades themselves under each
criterion by answering questions such as: How
much better is a student applicant with excellent
grades than one with very good grades? and how
much better is a student applicant with average
letters of recommendation than one with poor
ones? and so on. The alternatives are not pairwise
compared, but simply rated as to what category in
which they fall under each criterion. A weighting
and summing process yields their overall ranks.
This will become clear in the second example
below. There is no reason why forcing standards
on a problem should produce the same outcome
obtained through relative measurement. These are
two different descriptive (what can be) and
normative (what should be) settings.
4.1. Relative measurement: Choosing the best house
to buy
When advising a family of average income to
buy a house, the family identified eight criteria
which they thought they had to look for in a
house. These criteria fall into three categories:
economic, geographic and physical. Although one
may have begun by examining the relative impor-
tance of these clusters, the family felt they wanted
to prioritize the relative importance of all the
criteria without working with clusters. The prob-
lem was to decide which of three candidate houses
to choose. The first step is the structuring of the
problem asa hierarchy.
In the first (or top) level is the overall goal of
'Satisfaction with house'. In the second level are
the eight criteria which contribute to the goal, and
the third (or bottom) level are the three candidate
houses which are to be evaluated in terms of the
criteria in the second level. The definitions of the
criteria follow and the hierarchy is shown in Fig-
ure 1.
The criteria important to the individual family
were:
(1) Size of house: Storage space; size of rooms,
number of rooms; total area of house.
(2) Location to bus lines: Convenient, close bus
service.
SAT, SFACTION W IT ""O U SE ]
Figure 1. Decomposition of the probl em i nt o a hierarchy
T.L. Saat y / The AHP: How to mak e a decision 15
Tabl e l
The f u n d a me n t a l scale
I nt e ns i t y of i mp o r t a n c e De f i ni t i on Expl a na t i on
o n a n abs ol ut e scale
1 Equal i mp o r t a n c e
3 Mode r a t e i mp o r t a n c e of
one over a not he r
5 Essent i al or s t r ong i mpor -
t ance
7 Very s t r ong i mp o r t a n c e
9
2 , 4 , 6 , 8
Reci pr ocal s
Ra t i ona l s
Ext r e me i mp o r t a n c e
I n t e r me d i a t e va l ue s be-
t ween t he t wo adj acent
j u d g me n t s
Two act i vi t i es c ont r i but e equal l y t o t he obj ect i ve
Exper i ence a nd j u d g me n t s t r ongl y f avor one act i vi t y over a not he r
Exper i ence a nd j u d g e me n t s t r ongl y f a vor one act i vi t y over a not he r
An act i vi t y is s t r ongl y f avor ed a nd i t s d o mi n a n c e d e mo n s t r a t e d in
pr act i ce
The evi dence f avor i ng one act i vi t y over a n o t h e r is of tile hi ghes t
pos s i bl e or de r of a f f i r ma t i on
Wh e n c o mp r o mi s e is needed
I f act i vi t y i ha s one of t he above n u mb e r s as s i gned t o it wh e n c o mp a r e d wi t h act i vi t y j , t hen j has
t he r eci pr ocal val ue whe n c o mp a r e d wi t h i
Ra t i os ar i si ng f r om t he scale I f c ons i s t e nc y wer e t o be f or ced by obt a i ni ng n numer i cal val ues t o
s pa n t he ma t r i x
(3) Neighborhood: Little traffic, secure, nice
view, low taxes, good condition of neighborhood.
(4) Age of house: Self-explanatory.
(5) Yard space: Includes front, back and side,
and space from neighbors.
(6) Modern facilities: Dishwashers, garbage dis-
posals, air conditioning, alarm system, and other
such items possessed by a house.
(7) General condition: Repairs needed, walls,
carpet, drapes, cleanliness, wiring.
(8) Financing available: Assumable mortgage;
seller financing available, or bank financing.
The second step is the elicitation of pairwise
comparison judgments. Arrange the elements in
the second level into a matrix and elicit judgments
from the people who have the problem about the
relative importance of the elements with respect to
the overall goal, Satisfaction with House. The
scale to use in making the judgments is given in
Table 1. This scale has been validated for effec-
tiveness, not only in many applications by a num-
ber of people, but also through theoretical com-
parisons with a large number of other scales.
The questions to ask when comparing two
Ta bl e 2
Pai r wi se c o mp a r i s o n ma t r i x f or level 1
1 2 3 4 5 6 7 8 Pr i or i t y
vect or
I I
1 1 5 3 7 6 6 ~ a 0.173
I 1 I
2 ~ 1 ~ 5 3 3 t ~ 0.054
I
3 ~ 3 1 6 3 4 6 ~, 0.188
4 t 7 i 1 i i ; i
6 1 3 a v ~ 0.018
5 ~ ~ ~ ~ ;
3 3 3 1 ~ 5 6 0.031
6 ~ ~ ~ ~
a 4 2 1 ~ 6 0.036
1 I
7 3 5 ~ 7 5 5 1 ~ 0.167
8 4 7 5 8 6 6 2 1 0.333
~'max = 9.669, CI = 0.238, CR ~ 0.169
16 T.L. Saaty / The AHP: How to make a decision
criteria are of the following kind: of the two
criteria being compared, which is considered more
i mport ant by the fami l y buyi ng the house with
respect to the overall goal of fami l y satisfaction
with the house?
When the elements being compared are closer
together t han indicated by the scale, one can use
the scale 1.1, 1.2 . . . . . 1.9. If still finer, one can use
the appropriate percentage refinement.
The matrix of pairwise comparisons of the
criteria given by the homebuyers in this case is
shown in Table 2, along with the resulting vector
of priorities. The vector of priorities is the prin-
cipal eigenvector of the matrix. It gives the relative
priority of the criteria measured on a ratio scale.
In this case financing has the highest pri ori t y with
33% of the influence.
In Table 2, instead of nami ng the criteria, we
use the number previously associated with each.
Next we move to the pairwise comparisons of the
elements in the lowest level. The elements to be
compared pairwise are the houses with respect to
how much better one is t han the other is satisfying
each criterion in level 2. Thus there will be eight
3 x 3 matrices of j udgment s since there are eight
elements in level 2, and 3 houses to be pairwise
compared for each element. Again, the matrices
cont ai n the j udgment s of the fami l y involved. To
underst and the j udgment s, a brief description of
the houses follows.
House A. This house is the largest of t hem all.
It is located in a nei ghborhood with little traffic
and low taxes. Its yar d space is comparabl y larger
t han houses B and C. However, the general condi-
t i on is not very good and it needs cleaning and
painting. Also, the fi nanci ng is unsat i sfact ory be-
cause it woul d have to be bank-fi nanced at high
interest.
House B. This house is a little smaller t han
House A and is not close to a bus route. The
nei ghborhood gives one the feeling of insecurity
because of traffic conditions. The yard space is
Ta b l e 3
Co mp a r i s o n ma t r i c e s a n d l oc a l p r i o r i t i e s
Si ze of h o u s e A B C Pr i o r i t y Ya r d s p a c e A B C Pr i o r i t y
v e c t o r ve c t or
A
B
C
Tr a n s p o r t a t i o n
1 6 8 0. 754 A 1 5 4 0. 674
I
1 4 0. 181 B -~ 1 0. 101
I 1 1
z 1 0. 065 C z 3 1 0. 226
~ m a x = 3. 136, CI = 0. 068, C R = 0. 117 ~kma x = 3. 086, CI = 0. 043, C R = 0. 074
A B C Pr i o r i t y Mo d e m A B C Pr i o r i t y
v e c t o r f a c i l i t i e s v e c t o r
A
B
C
Ne i g h b o r h o o d
1 7 0. 233 A 1 8 6 0. 747
1 1 1 1
1 ~ 0. 005 B ~ 1 5 0. 060
1
5 8 1 0. 713 C ~ 5 1 0. 193
~kma x = 3. 247, CI = 0. 124, C R = 0. 213 ~max = 3. 197, CI = 0. 099, C R = 0. 170
A B C Pr i o r i t y Ge n e r a l A B C Pr i o r i t y
v e c t o r c o n d i t i o n ve c t or
A
B
C
Ag e of hous e
I 1
1 8 6 0. 745 A 1 ~ ~ 0. 200
1 1 1 0. 065 B 2 1 1 0. 400
g
1 4 1 0. 181 C 2 1 1 0. 400
h m a x = 3. 130, CI = 0. 068, C R = 0. 117 ~ m a x = 3 . 0 0 0 , C I = 0 . 0 0 0 , C R = 0 . 0 0 0
A B C Pr i o r i t y F i n a n c i n g A B C Pr i o r i t y
ve c t or v e c t o r
A
B
C
| 1 0 . 0 7 2
1 1 1 0. 333 A 1 v
1 1 1 0. 333 B 7 1 3 0. 650
1
1 1 1 0. 333 C 5 3 1 0. 278
?~max = 3. 000, c f = 0. 000, C R = 0. 000 ~max = 3. 065, CI = 0. 032, C R = 0. 056
T L . Saat y / The AHP: How to mak e a decision 17
Table 4
Local and global priorities
1 2 3 4 5 6 7 8
(0.173) (0.054) (0.188) (0.018) (0.031) (0.036) (0.167) (0.333)
A 0.754 0.233 0.754 0.333 0.674 0.747 0.200 0.072 0.396
B 0.181 0.055 0.065 0.333 0.101 0.060 0.400 0.650 0.341
C 0.065 0.713 0.181 0.333 0.226 0.193 0.400 0.278 0.263
fairly small and the house lacks the basic moder n
facilities. On the other hand, the general condi t i on
is very good. Also, an assumable mort gage is
obt ai nabl e which means the financing is good with
a rather low interest rate.
House C. House C is very small and has few
modern facilities. The nei ghborhood has high
taxes, but is in good condi t i on and seems secure.
The yard space is bigger t han t hat of House B, but
is not comparabl e to House A' s spacious sur-
roundings. The general condi t i on of the house is
good and it has a pret t y carpet and drapes.
The matrices of comparisons of the houses wi t h
respect to the criteria and their local priorities are
given in Table 3.
The third step is to establish the composite or
global priorities of the houses. We lay out the
local priorities of the house with respect to each
criterion in a mat ri x and mul t i pl y each col umn of
vectors by the pri ori t y of the corresponding crite-
rion and add across each row which results in the
desired vector of the houses in Table 4. House A
which was the least desirable with respect to fi-
nanci ng (the highest pri ori t y criterion), cont rary to
expectation, had the largest priority. It was the
house t hat was bought.
4.2. Absolute measurement: Employee evaluation
Absol ut e measurement is applied to rank alter-
natives in terms of ratings, intensities or grades of
the criteria. These grades may take the form:
excellent, very good, good, average, below average,
poor and very poor. Aft er establishing a scale of
priorities for the criteria (or subcriteria, if there
are some) t hrough pai red comparisons, the grades
which may be di fferent for each criterion or sub-
criterion~ are in t urn pairwise compared according
Table 5
The hierarchy of employee evaluation
Goal:
Criteria: Technical
Intensities:
Employee performance evaluation
Maturity Writing Verbal Timely Potential
skills skills work (personal)
(0.061) (0.196) (0.043) (0.071) (0.162) (0.466)
Excell. Very Excell. Excell. Nofollup Great
(0.604) (0.731) (0.733) (0.750) (0.731) (0.750)
Abv. avg. Accep. Avg. Avg. On time Averag.
(0.245) (0.188) (0.199) (0.171) (0.188) (0.171)
Avg. Immat. Poor Poor Remind Bel. avg.
(0.105) (0.181) (0.068) (0.078) (0.081) (0.078)
Bel. avg.
(0.046)
Alternatives:
(1) Mr. X Excell. Very Avg. Excell. On time Great
(2) Ms. Y Avg. Very Avg. Avg. Nofollup Avg.
(3) Mr. Z ExceU. Immat. Avg. Excell. Remind Great
18 T.L. S a a t y / The A H P : Ho w t o m a k e a deci si on
to t hei r par ent cri t eri on. An al t er nat i ve is
eval uat ed, for each cri t eri on or subcri t eri on, by
i dent i fyi ng the gr ade which best descri bes it. Fi-
nally, the wei ght ed or gl obal pri ori t i es of the grades
are added to pr oduce a rat i o scale for the al t erna-
tive. Absol ut e meas ur ement needs st andar d to
make it possi bl e to j udge whet her the al t ernat i ve is
accept abl e or not. Absol ut e meas ur ement is useful
in st udent admi ssi on, facul t y t enure and pr omo-
tion, empl oyee eval uat i on, and in ot her areas where
t here is fai rl y good agr eement on st andar d whi ch
are t hen used to rat e al t ernat i ves one at a time.
Let us consi der an abbr evi at ed versi on of the
pr obl em of eval uat i ng empl oyee per f or mance. The
hi erarchy for t he eval uat i on and the pri ori t i es
deri ved t hrough pai r ed compar i sons are shown
below. It is t hen fol l owed by a rat i ng of each
empl oyee for the qual i t y of per f or mance under
each cri t eri on and summi ng the resul t i ng scores of
obt ai n his overall rating. The hi er ar chy in Tabl e 5
can be mor e el aborat e, i ncl udi ng subcri t eri a, fol-
l owed by t he intensities for expressi ng quality.
Let us now show how to obt ai n the t ot al score
for Mr. X (see Tabl e 5):
0.061 X 0.604 + 0.196 X 0.731 + 0.043 0.199
+ 0.071 x 0.750 + 0.162 X 0.188
+ 0.466 x 0.750 = 0.623.
Si mi l arl y the score for Ms. Y and Mr. Z can be
shown to be 0.369 an 0.478 respectively. I t is cl ear
t hat we can r ank any number of candi dat es al ong
these lines. Her e the vect or of pri ori t i es of the
cri t eri a has been wei ght ed by the vect or of rel at i ve
number of intensities under each cri t eri on and
t hen renormal i zed. We call this a st ruct ural rescal-
ing of the priorities.
5. T h e o r e t i c a l c o n s i d e r a t i o n s [7]
There is a well known pri nci pl e in mat hemat i cs
t hat is wi del y pract i ced, but sel dom enunci at ed
wi t h sufficient forceful ness to i mpr ess its i mpor -
tance. A necessary condi t i on t hat a pr ocedur e for
solving a pr obl em be a good one is t hat if it
pr oduces desi red results, and we per t ur b the vari a-
bles of the pr obl em in some small sense, it gives us
results t hat are ' cl ose' to the ori gi nal ones. Thi s is
preci sel y the use of cont i nui t y and uni f or m con-
t i n u i t y - - t o assure t hat af t er t r ansf or mi ng a vari a-
ble, originally near by val ues go over to near by
values. An ext ensi on of this phi l osophy in pr ob-
l ems where or der rel at i ons bet ween the vari abl es
are i mpor t ant , is t hat on small per t ur bat i ons of
the vari abl es, the pr ocedur e pr oduces close, or der
pr eser vi ng results. The pr ocedur e descri bed here
has this charact eri st i c.
Because of the nat ur al way in which a mat r i x of
rat i os and smal l per t ur bat i ons of t hat mat r i x lead
to a pr i nci pal ei genval ue pr obl em, one may st art
wi t h this and general i ze to posi t i ve mat ri ces t hat
need not be reci procal . The Ge r ma n mat hemat i -
ci an Os kar Per r on pr oved in 1907 that, if A- -
( a i j ) , a u > O, i , j = 1 . . . . . n , t hen A has a si mpl e
posi t i ve ei genval ue ~m~x (called the pr i nci pal ei-
genval ue of A) and ~ k m a x ~ > ] ~ k k I for t he r emai ni ng
ei genval ues of A. Fur t her mor e, t he pr i nci pal ei-
genvect or w = (w I . . . . . w, ) v t hat is a sol ut i on of
A w = ~m~x w has w~ > 0, i = 1 , . . . , n. We can write
t he nor m of the vect or w as I l wl l = e Tw where
e = (1, 1 . . . . . 1) T and we can nor mal i ze w by divid-
ing it by its nor m. For uni queness, when we refer
to w we mean its nor mal i zed form. Our pur pos e
here is to show how i mpor t ant the pr i nci pal eigen-
vect or is in det er mi ni ng the r ank of the al t erna-
tives t hr ough domi nance walks.
We have seen t hat r at i o scale est i mat i on has a
nat ur al set t i ng in pr i nci pal ei genval ue f or mul a-
tion. We will now show t hat in addi t i on, the
pr i nci pal ei genvect or al so has the or der preservi ng
pr oper t i es we seek.
When A is consi st ent , one way to defi ne the
or der of t he al t ernat i ves is to requi re t hat one row
of the mat r i x domi nat e el ement wi se anot her row.
But when A is i nconsi st ent it is no l onger possi bl e
to defi ne domi nance in this manner . Inst ead, we
bor r ow t he concept of domi nance f r om gr aph
t heor y where the sum of t he coeffi ci ent s in each
r ow of A is used. Thi s concept carri es over in a
nat ur al way to the i nconsi st ent case. But we must
l ook at a di f f er ent way t o capt ur e domi nance by
consi deri ng f ur t her possi bi l i t i es not si mpl y f r om
t he mat r i x i t sel f or some ar bi t r ar y power of it, but
f r om all its powers.
The mat r i x A capt ur es onl y t he domi nance of
one al t er nat i ve over every ot her in one step. But
an al t ernat i ve can domi nat e a second by first
domi nat i ng a t hi rd al t er nat i ve and t hen the t hi rd
domi nat es the second. Thus, the first al t ernat i ve
domi nat es t he second in t wo steps. I t is known
t hat the resul t for domi nance in t wo st eps is
obt ai ned by squar i ng the pai rwi se compar i s on ma-
T.L. Saaty / The AHP: How to make a decision 19
trix. Similarly, domi nance can occur in t hree steps,
four steps and so on, the val ue of each is obt ai ned
by raising t he mat r i x to the cor r espondi ng power.
The r ank or der of an al t ernat i ve is the sum of t he
relative val ues for domi nance in its row, in one
step, two st eps and so on averaged over the num-
ber of steps. The quest i on is whet her this average
t ends to a meani ngf ul limit. I t is easy to see t hat it
does when A is consi st ent because A k = n k- 1A.
We can t hi nk of t he al t ernat i ves as t he nodes of
a di rect ed graph. Wi t h every di rect ed arc f r om
node i to node j (which need not be distinct), is
associ at ed a nonnegat i ve numbe r ai j of the domi -
nance mat ri x. I n gr aph- t heor et i c t er ms this is the
i nt ensi t y of the arc. Def i ne a k- wal k to be a
sequence of k arcs such t hat the t er mi nat i ng node
of each arc except the l ast is the source node of
the arc whi ch succeeds it. The intensity of a k-wal k
is the pr oduct of the intensities of the arcs in the
walk. Wi t h these ideas, we can i nt er pr et the mat r i x
Ak: the (i, j ) ent r y of A k is the sum of the
intensities of all k-wal ks f r om node i to node j .
Defi ni t i on. The domi nance of an al t ernat i ve al ong
all walks of length k ~< m is gi ven by
1 m A%
m ~-" e'rA% " (3)
k=l
Obser ve t hat the ent ri es of A% are t he row sums
of A k and t hat eVA% is the sum of all the ent ri es
of A.
T h e o r e m 3. The dominance of each alternative along
all walks k, is given by the solution of the eigenvalue
problem A w = X max W.
Pr o o f . Let
Ak e
s k eTA% (4)
and
1 m
tm = m E sk. ( 5 )
k=l
The convergence of the component s of tm to the
same limit as the component s of s, , is the st and-
ard Cesar o summabi l i t y. Since
Ake
' w as k---, m, (6)
s k - eTAk e
where w is the nor mal i zed pr i nci pal right eigen-
vect or of A, we have
1 ~ A%
tm = -~ eVAk------ ~ -~ w as m ~ ~ . (7)
k=l
The sol ut i on of t he ei genval ue pr obl em is ob-
t ai ned by rai si ng t he mat r i x A to a suffi ci ent l y
l arge power t hen s ummi ng over the rows and
nor mal i zi ng to obt ai n t he pr i or i t y vect or w =
(w 1 . . . . . wn) ~. The process is st opped when the
di fference bet ween component s of the pri ori t y
vect or obt ai ned at the k- t h power and at the
( k + 1)st power is less t han some pr edet er mi ned
small value.
I n reference [7] we gave at l east five di fferent
ways of deri vi ng the pri ori t i es f r om the mat r i x of
pai r ed compar i sons. Besides the ei genvect or solu-
tion, these i ncl ude the di rect row sum average, the
nor mal i zed col umn average, and met hods which
mi ni mi ze t he sum of t he errors of the di fferences
bet ween the j udgment s and t hei r deri ved val ues
such as the met hods of l east squares and l ogari t h-
mi c least squares. We poi nt ed out t hat the loga-
ri t hmi c least squares sol ut i on coi nci des wi t h the
pr i nci pal ri ght ei genvect or sol ut i on for mat ri ces of
or der n = 3, whi ch is t he first val ue of n for which
i nconsi st ency is possi bl e and l eft and right eigen-
vect ors are reci procal s of each ot her whi ch is not
al ways t he case for l arger val ues of n. Since the
appear ance of the Anal yt i c Hi er ar chy Process in
the l i t erat ure, ot her met hods have been pr opos ed
[7,15]. All met hods yield the same answer when
the mat r i x is consi st ent . The combi ned use of a
measur e of i nconsi st ency whi ch can be deri ved in
t er ms of bot h l eft and right ei genvect ors, al ong
wi t h the ri ght ei genvect or sol ut i on which capt ur es
the domi nance expr essed in t he j udgment s, is an
effect i ve way to l ook at t he pr obl em. We argue
t hat so l ong as i nconsi st ency is t ol erat ed, domi -
nance is t he basi c t heoret i cal concept for deri vi ng
a scale and no ot her met hod qualifies. In addi t i on,
a count er exampl e has been pr ovi ded in which the
met hod not onl y does not generat e a good ap-
pr oxi mat i on, but al so reverses rank. Some have
even resort ed to artificial axi omat i zat i on t hi nki ng
t hat it gives a met hod the appear ance of rigor,
al t hough axi oms are assumpt i ons not proofs. It
may be t hat the ar i t hmet i c of a met hod is si mpl er
t han t hat used to obt ai n the ei genvect or, but t hat
no l onger mat t er s, because of the wi despr ead use
20 T.L. Saaty / The AHP: How to make a decision
of the comput er . I t is r easonabl e to argue t hat a
t heory for maki ng sound deci si ons mus t st and on
cl earl y j ust i fi abl e grounds.
The soft ware package Exper t Choice, useful in
t eachi ng and in real appl i cat i ons, can handl e bot h
rel at i ve and absol ut e measur ement , as well as hav-
ing special capabi l i t i es such as st ruct ural rescaling,
combi ni ng gr oup j udgment s, sensi t i vi t y anal ysi s
and dependence among the deci si on al t ernat i ves
[2]. The reader i nt erest ed in pur sui ng t he subj ect
f ur t her shoul d consul t references [3,7,8,13,15].
6. No r ma l i z a t i o n - Sc a r c i t y a nd a bunda nc e
Nor mal i zat i on in the AHP is not j ust a mecha-
ni cal operat i on. I t cont ai ns i nf or mat i on on the
t ot al domi nance of the al t ernat i ves bei ng com-
par ed whi ch enabl es us to appor t i on the pr i or i t y
of the cri t eri on t o each al t ernat i ve accor di ng to
the relative domi nance of the al t ernat i ve.
Nor mal i zat i on can al so be associ at ed wi t h t he
i dea of scarci t y and abundance of the pr esence of
a cri t eri on in the al t ernat i ves such as redness in
fruit. Too ma ny fruits t hat are red make red
abundant and uni mpor t ant in di fferent i at i ng be-
t ween i ndi vi dual fruits. Conversel y, if redness oc-
curs i nt ensel y in some fruits but not in ot hers, it is
t hus scarce and can be used as a cri t eri on to
di fferent i at e in maki ng a decision among fruits.
Thus, the great er the cont r ast among t he al t erna-
tives, the mor e useful is the pri ori t y val ue of t he
cri t eri on al l ot t ed t o each. Conversel y, when for
exampl e, the cont r ast of the al t ernat i ves is smal -
lest (when t he t ot al domi nance is equal to n 2, see
bel ow) and hence all the al t ernat i ves are alike, t he
por t i on of t he cri t eri on pr i or i t y assi gned to each is
equal. Thus a cri t eri on wi t h respect to whi ch t here
is great er cont r ast and domi nance among t he al-
t ernat i ves is ' s car ce' and consequent l y mor e in-
fl uent i al in det er mi ni ng r ank t han anot her crite-
ri on on whi ch t here is no di st i nct i on among the
al t ernat i ves, i.e., t hei r mat r i x of pai r ed compar i -
sons has mor e l ' s in it. I n bei ng scarce, mor e of
t he cri t eri on is al l ot t ed to t he mor e domi nant
al t ernat i ve and hence it affect s t he fi nal r anki ng of
t hat al t ernat i ve more.
An ' a bunda nt ' cri t eri on cont r i but es less t o r ank
det er mi nat i on because it cont r i but es an equal or
nearl y equal pr i or i t y to each al t ernat i ve and when
t he sum is t aken over t he cri t eri a it has little effect
in det er mi ni ng r ank (recall t hat i f a > b t hen
a + c > b + c and c does not reverse order). An
al t ernat i ve t hat is a copy of anot her can di l ut e t he
pr i or i t y of a decisive cri t eri on so t hat it is no
l onger t he cont r ol l i ng one in det er mi ni ng the final
rank. We have:
T h e o r e m 4. ~ i j a i j = n 2, i f and onl y i f al l al t er na-
t i ves hav e equal domi nanc e , i . e. , ai j = 1, i, j =
1 . . . . , n, wi t h r es pect to a cri t eri on.
I t is easy to see t hat n 2 is the mi ni mum val ue
of possi bl e t ot al domi nance by a pai r ed compar i -
son of n al t ernat i ves. The ma xi mum val ue is,
usi ng 9 as t he upper r ange of t he scale of pai r ed
compar i sons, [ n( n - 1)](9 + ~) + n = ~(41n 2 -
32n).
Our di scussi on of absol ut e and rel at i ve meas-
ur ement ma y be f r amed in economi c t erms. I n
absol ut e measur ement , val ue and ne e d are identi-
cal; ' t he mor e val ue, t he bet t er t he need is satis-
fied' . I n rel at i ve measur ement , val ue is assessed in
t er ms of need. Her e surpl us val ue may or ma y not
sat i sfy mor e need. I n fact, t here are i nst ances
where sat i at i on t akes pl ace and abundance can
l ead to a decline in t he sat i sfact i on of need.
7. Cl us t e r i ng
Compar i s ons of el ement s in pai rs requi res t hat
t hey be homogeneous or close wi t h respect to t he
c ommon at t r i but e; ot her wi se si gni fi cant errors
ma y be i nt r oduced i nt o t he process of measur e-
ment . I n addi t i on, t he numbe r of el ement s bei ng
compar ed mus t be smal l (not mor e t han 9) to
i mpr ove consi st ency and t he cor r espondi ng accu-
r acy of measur ement . For exampl e, we ma y clus-
t er appl es in one way accor di ng t o size, in anot her
way accor di ng to col or and in still anot her way
accor di ng t o age. The quest i on t hen is how to
pe r f or m cl ust eri ng of homogeneous el ement s in an
effi ci ent way to faci l i t at e pai r ed compar i sons.
Cl ust eri ng is a pr ocess of gr oupi ng el ement s wi t h
respect to a c ommon pr oper t y. One can t hen
decompos e the set of or der ed el ement s wi t h re-
spect to an at t r i but e i nt o cl ust ers of, for exampl e,
seven el ement s each, f r om l argest to smallest. The
smal l est el ement of t he l argest cl ust er is i ncl uded
as one of t he seven el ement s of the next cluster.
The rel at i ve wei ght s of all t he el ement s in this
T.L. Saat y / The AHP: How to mak e a decision 21
second cl ust er are di vi ded by the wei ght of t he
c ommon el ement and t hen mul t i pl i ed by its wei ght
in the first cl ust er in this manner bot h cl ust ers
become commens ur at e and are pool ed t oget her.
The process is t hen r epeat ed to t he r emai ni ng
clusters. Somet i mes one may need to i nt r oduce
hypot het i cal el ement s in or der to preserve the
gr adual descent f r om l arge to small.
We discuss t hree ways as t o how to per f or m
cl ust eri ng on the al t ernat i ves of a decision pr ob-
l em whose numbe r may be very large and needs a
di fferent sort i ng for each of several at t ri but es.
They are or der ed in t he fol l owi ng di scussi on f r om
t he least to the mos t effi ci ent way.
7.1. The elementary approach
or der on t hat at t ri but e. They can t hen be cl ust ered
i nt o smal l gr oups as descr i bed above and pai rwi se
compar ed.
One r eason why absol ut e meas ur ement ma y not
be desi rabl e is t hat it is st rongl y subjective. I n
pai r ed compar i sons, meas ur ement is based on ob-
ser vat i on of the rel at i ve i nt ensi t y of a pr oper t y
bet ween t wo el ement s. Absol ut e meas ur ement is
based on obser vat i ons st ored in me mor y whi ch
depend on exper i ence and on the abi l i t y to recall
it. For ma ny pr obl ems, it is useful to first car r y
out absol ut e meas ur ement t o sort and cl ust er the
el ement s, and t hen fol l ow t hat wi t h rel at i ve meas-
ur ement for great er accuracy. Thi s is par t i cul ar l y
rel evant in pr edi ct i ng mos t likely out comes whi ch
i nvol ve syner gy a mong t he al t ernat i ves.
Gi ven n el ement s in a level of the hi erarchy,
one may first make a pass t hr ough t hem by com-
par i ng one el ement wi t h anot her, dr oppi ng it and
pi cki ng anot her if t hat one is percei ved t o be
l arger and cont i nui ng t he compar i son. Thus, t he
l argest el ement is selected in n - 1 such compar i -
sons. The process is r epeat ed for the r emai ni ng
n - 1 el ement s t o i dent i fy the second l argest ele-
ment and so on. I n t he end, the el ement s woul d be
ar r anged in descendi ng order of size or i nt ensi t y
accordi ng to an at t r i but e and are sequent i al l y
cl ust ered i nt o groupi ngs of a few el ement s each
f r om the l argest to t he smallest. Thi s process is
hi ghl y i neffi ci ent and requi res t he ast r onomi cal
numbe r of (n - 1)! compar i sons.
7.2. Trial and error clustering
The al t ernat i ves ma y be put i nt o gr oups of
large, medi um and small. Then t he el ement s in
each gr oup are put i nt o several cl ust ers of a few
el ement s each, and a first pass at compar i sons is
used to i dent i fy mi sfi t s which are t hen t aken out
and put i nt o the appr opr i at e one of t he ot her t wo
categories. Recl ust eri ng is t hen per f or med and
compar i sons are carri ed out. I f el ement s are f ound
not to fit, t hey are agai n moved to the appr opr i at e
cat egory. Thi s process is r epeat ed for each at t ri -
but e.
7.3. Clustering by absolute measurement
Each al t ernat i ve is eval uat ed by absol ut e meas-
ur ement for an at t ri but e, and t hus in descendi ng
8. Co mb i n i n g r e l at i ve and a bs o l ut e me a s u r e me n t -
C o s t - b e n e f i t a na l y s i s
An easy pi t fal l for an i ndi vi dual who has j ust
l earned about t he AHP is to t ake t wo or mor e
cri t eri a on whi ch al t ernat i ves are measur ed on the
same exi st i ng s t andar d scale, such as dol l ars or
ki l ograms, nor mal i ze each set and t hen compos e
wi t h respect to t he criteria. One qui ckl y di scovers
t hat t he answer is not t he same as t hat obt ai ned
t hr ough t he usual ar i t hmet i c and hast i l y concl udes
t hat the AHP is at fault. To avoi d this pr obl em,
one mus t exercise caut i on in conver t i ng measur e-
ment s on a st andar d scale to rel at i ve val ues when
several such cri t eri a are i nvol ved [9].
For t he ar i t hmet i c to conf or m wi t h what one
or di nar i l y does, assign each cri t eri on a pr i or i t y
t hat is t he sum of t he meas ur ement s of the alter-
nat i ves wi t h respect t o it, di vi ded by the sum of
the meas ur ement s of all the al t ernat i ves under all
t he cri t eri a meas ur ed wi t h t hat unit. To fi nd the
compos i t e pr i or i t y for each al t ernat i ve mul t i pl y
the cri t eri on wei ght by its cor r espondi ng nor mal -
ized wei ght under t hat cri t eri on and sum over the
criteria. The resul t ma y be consi der ed as the wei ght
of the al t er nat i ve wi t h respect to one super crite-
ri on compos ed of all t he cri t eri a wi t h the uni t of
measur ement . That super cri t eri on may t hen be
c ompa r e d wi t h ot her i nt angi bl e cri t eri a and ot her
super cri t eri a wi t h di f f er ent uni t s of measur ement .
Al t ernat i vel y, one can per f or m pri ori t y compar i -
sons on all the dat a avai l abl e wi t hout ascri bi ng
l i neari t y to t hem as one or di nar i l y does wi t h num-
22 T.L. Saaty / The AHP: How to make a decision
bers. That is t o say, one i nt erpret s what the num-
bers mean and uses j udgment r at her t han cr anki ng
t he number mechani cal l y. Wi t h r ar e except i on, the
j udgement appr oach is by far t he mor e effect i ve
pr ocedur e usi ng t he AHP to deal wi t h the underl y-
ing compl exi t y of a deci si on pr obl em, and one
need not be afrai d to do it. I t is known t hat scales
are i nvent ed to faci l i t at e communi cat i on, and mus t
be experi enced for a l ong t i me bef or e t hey can be
associ at ed wi t h our val ue syst em, duri ng whi ch
t i me t hey al most al ways are modi fi ed.
The AHP is a descri pt i ve t heory. Therefore, it
is not an aut omat i c set -up for accommodat i ng any
nor mat i ve appr oach such as utility maxi mi zat i on.
I t needs t o be i nt er pr et ed and adapt ed for t hat
purpose. I t is even mor e difficult when a nor ma-
tive t heory has ma ny except i ons so the AHP i nt er-
pr et at i on woul d not be universal. I n utility maxi -
mi zat i on it is assumed t hat it is al ways t he case
t hat the mor e utility or mor e mone y the bet t er,
but there are ma ny i nst ances when this is not true.
For exampl e, a gover nment agency t hat is l eft
wi t h mor e money at the end of t he year, gets a
smal l er al l ocat i on in a fut ure budget . A rich indi-
vi dual in a poor count r y under revol t by t he poor
is likely to get killed. The avai l abi l i t y of money is
of t en an i ncent i ve to use money where ot her alter-
nat i ves coul d be mor e effective. Thus, AHP adap-
t at i on for utility cal cul at i on pur poses needs to
t ake such caveat s i nt o consi derat i on. One i dea to
keep in mi nd wi t h t he AHP is t hat the mont oni c-
i t y of utilities need not be pr eser ved and ma y be
cont radi ct ed.
The foregoi ng has bear i ng on benef i t - cos t
analyses. Expect ed utilities are used for r epeat ed
deci si on maki ng. I n t hat case, benef i t cost anal ysi s
f r om two hi erarchi es is appl i ed, and f r om it one
can also cal cul at e mar gi nal benef i t to cost ratios.
Resour ce al l ocat i on may be made by usi ng benef i t
to cost rat i os thus derived. Short range deci si ons
of t en include l ow costs as benefi t s in a single
hi erarchy. Thi s is a useful appr oach when a deci-
si on to spend money on one of several opt i ons has
al r eady been made. I t is one way t o combi ne
benefi t s and cost s as one does wi t h dol l ars by
t aki ng differences. I n t he AHP one does not use
differences. I n such one- t i me decisions, cost s ma y
be regarded as i nverse benefi t s so t hat benefi t s,
l ow costs and ot her i nconveni ences are used to
est abl i sh pri ori t i es for t he al t ernat i ves.
If, on t he ot her hand, benefi t s and cost s are
measur ed in dol l ars al ong wi t h i nt angi bl e fact ors,
t hey must first be compos ed accor di ng to t he
dol l ars and t hen combi ned wi t h the i nt angi bl e
cri t eri a as descr i bed earlier. Mar gi nal benefi t cost
anal ysi s al ong t r adi t i onal lines can be carri ed out
by ar r angi ng t he cost s in i ncreasi ng order, and
t hen f or mi ng rat i os of successive di fferences of
benefi t s and cost s in t hat order. The very first
rat i o is t hat of t he al t er nat i ve wi t h the smal l est
cost. Then one f or ms t he r at i o of di fferences wi t h
t hat bet ween t he next hi ghest cost and the smal l est
one in t he denomi nat or , and the cor r espondi ng
di fference in benef i t s in the numer at or . Whenever
a di fference in a nume r a t or is negat i ve, t hat suc-
ceedi ng al t er nat i ve is dr opped f r om consi derat i on.
I n this manner , the al t er nat i ve yi el di ng t he highest
mar gi nal r at i o is chosen.
The next quest i on is how to fi nd a r easonabl e
way to combi ne benef i t s ( B) and cost ( C) , when a
r at i o r at her t han a single hi er ar chy are used [10].
Thi s is useful in consi deri ng confl i ct pr obl ems
i nvol vi ng mor e t han one val ue system. Since the
hi er ar chy of cost s l eads to a vect or of val ues
i ndi cat i ng rel at i ve ma x i mu m costs, t he reci procal s
of t he ent ri es of this vect or coul d be t hought of as
t he mi ni mum cost s i ncur r ed in j oi nt l y maxi mi zi ng
benefi t s and mi ni mi zi ng costs. I n general, the out -
comes f r om a hi er ar chy of benefi t s and a hi er ar chy
of cost s are t wo r at i o scales whose cor r espondi ng
rat i os l ead to a meani ngf ul r at i o scale. Thei r dif-
ferences woul d not be meani ngf ul .
To maxi mi ze B/ C is equi val ent to maxi mi zi ng
log B/ C, whi ch if B and C are close, may be
appr oxi mat ed by ( B/ C) - 1 or ( B- C) / C
known as r et ur n on i nvest ment , ROI . I f B and C
are not compar abl e, it woul d be initially cl ear t hat
onl y t he benefi t s or onl y the costs det er mi ne
whet her t he al l ocat i on shoul d be made or not .
Some peopl e have at t empt ed to compar e the
foregoi ng wi t h what is t r adi t i onal l y done in a
single cri t eri on choi ce pr obl em. An exampl e where
B- C al one gives rise to mi sl eadi ng results is
gi ven by my col l eague L. G. Vargas: You have $1
mi l l i on to i nvest t o get $1.101 mi l l i on or you have
$500000 t o i nvest to get $600000. Whi ch is a
bet t er i nvest ment ?
B - C anal ysi s gives: 1.101 - 1 = 0.101,
0.6 - 0.5 = 0. 1,
and the first al t er nat i ve woul d be chosen. ROI
T.L. Saat y / The AHP: How to mak e a decision 23
analysis yields 10.1% and 20%, respectively, and
the second al t ernat i ve which minimizes risk woul d
be correct l y chosen.
9. The s emi ot i c c o nne c t i o n
The Anal yt i c Hi er ar chy Process is a tool of
i nf or mat i on communi cat i on and signification. In a
general sense, it belongs to t he st udy of language
or semiotics. Semiotics or semiology is a codi ng in
which one considers signals rel at ed by a set of
rules or syntax; a set of states or cont ent s called a
semant i c system, a set of possible behavi oral re-
sponses i ndependent of the cont ent system, and a
rule associating signals with cont ent s or with be-
havi oral responses. The idea of a code covers all
four phenomena ment i oned above. Eco [1] uses
s-code for the first t hree and code for the fourt h.
Accordi ng to Morri s [5], the creat or of semi-
otics, semiosis is the process in which somet hi ng
funct i ons as a sign. He ment i ons t hat bot h man
and animals do r espond to cert ai n things as signs
of somet hi ng else, but t hei r compl exi t y in man is
f ound in speech, art, writing, and even medi cal
diagnoses. Science and signs are i nseparabl y inter-
connect ed. Semiotics, a step in the uni fi cat i on of
science, supplies the f oundat i ons for any science
of signs; linguistics, logic, mat hemat i cs, rhet ori c
and aesthetics.
In the Anal yt i c Hi er ar chy Process, words are
used for concept s i nvol ved in decisions. In a sense,
the pur pose of all i nf or mat i on is to deci de on
s omet hi ng- - even if it is an i magi nary hypothesis.
The hi erarchy is the syntax, t he subject of a deci-
sion is the semantic, pri ori t i zat i on is the rule asso-
ciating signals with cont ent , and behavi or com-
prises the possible decision alternatives. This way
of l ooki ng at the AHP needs to be highlighted and
emphasi zed to drive home the universality of the
decision process.
10. Cat ast rophe and t he A HP
One of the most burni ng quests we under t ake
using the knowl edge we acqui re is explaining and
forecasting, and in part i cul ar, forecast i ng catas-
trophes, or, mat hemat i cal l y speaking, sudden dis-
cont i nui t i es t hat affect t he or der of the alterna-
tives. This is a si t uat i on t hat is at odds with the
earlier mat hemat i cal pri nci pl e of small pert urba-
tions we gave in which small changes in i nput lead
to small changes in out comes. In cat ast rophes,
t here is a par t of t he pr obl em in which small
changes in condi t i ons at some critical value can
give rise to very large changes in out come. All we
can do is ei t her to ant i ci pat e and take strong
prevent i ve act i on or pr epar e ourselves in advance
with cont i ngency pl ans t oget her with emot i onal
accept ance for how to deal with t he emergency to
pay a smaller penal t y if it occurs, or be pr epar ed
to pay t he full penal t y havi ng accept ed t hat it
coul d happen. Because cat ast rophes are usually
unseen surprises, it gives us a feeling of cont rol to
t hi nk we can account for cat ast rophes in our daily
lives. Accordi ng to the di ct i onary, a cat ast r ophe is
a sudden disaster or happeni ng t hat causes great
har m or damage; a calamity. Even t he idea of
what const i t ut es a cat ast r ophe is relative. Some-
one whose life is t or ment ed by an opponent may
regard it as a blessing if a cat ast r ophe befalls the
t orment or. In ot her terms, a cat ast r ophe may be
regarded as a very st rong di scont i nui t y in think-
ing. How do we represent a cat ast rophe in terms
of the AHP?
In a cat ast r ophe t he el ement of surprise arises
f r om a shift in ranki ng of the out comes. Thus, if a
si t uat i on is ongoi ng a cert ai n choi ce of alternatives
may be i ndi cat ed, but a slight change in the situa-
tion may cause a sudden shift to anot her choice
t hat woul d have been previ ousl y very undesirable.
How can we allow for cat ast rophi c occurrences in
t he AHP?
One way to allow for a cat ast r ophe is to always
include a cri t eri on for t he unknown t hat repre-
sents a cl ust er of unf or seen threats. It may itself
have subcriteria. The alternatives are careful l y
pri ori t i zed with respect to this criterion for the
unexpect ed and its descendant s. The cri t eri on it-
self is assigned a low pri ori t y. Now we can imag-
ine t hat at each i nst ant t he j udgment s in the
criteria are flashed in their t ot al i t y on a screen
followed by t he best choi ce of alternatives. With
some changes in j udgment s, in general, choi ce is
stable and the changes in relative pri ori t y of the
al t ernat i ve slight. Af t er a cert ai n lapse of time,
t here is a sudden change in j udgment in the direc-
tion of this cri t eri on maki ng it mor e i mport ant .
The cor r espondi ng choi ce of alternatives is also
suddenl y changed surfaci ng a very undesirable
alternative. Thus, one mi ght i ncl ude among t he
24 T.L. Saaty / The AHP: How to make a decision
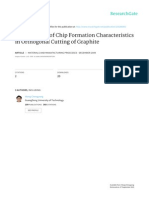
GOAL _ _
- ~ OLDWRECK
( 0 . 0 0 2 )
CHEVY
(0.009)
- - SIZE > - - > HONDA
(0. 0Sl ) (0.013)
--> TOYOTA
(0.026)
i
---~ OLDWRECK
(0.005)
CHEVY
_ OPERCOST > (0. 019)
(0.135) - > HONDA
(0.044)
" > TOYOTA
(0.067)
__> NORMAL
(0.99O)
- - STYLE
(0.269)
_ LOWPRICE
(0.535)
- - SIZE
(o .o o s)
_ OPERCOST
(0.001)
L~ ACCIDENT . ~
(oolo) - - - 3
- - STYLE
(0 .0 o 2 )
LOWPRICE
(0.001)
I
I
OLDWRECK
I
- - ' ~ (0.010)
CHEVY
(0 .0 8 6 )
--~ HONDA
(0.086)
TOYOTA
( 0 . 0 ~)
OLDWRECK
I ( 0 . 0 2 6 )
CHEVY
(0.081)
HONDA
(0.201)
TOYOTA
(0.227)
OLDWRECK
(0.004)
CHEVY
(0 .0 0 1 )
HONDA
(0 .0 0 0 )
TOYOTA
(0 .0 0 1 )
OLDW RECK
(o.001)
CHEVY
(0.00o)
HONDA
(0.00o)
TOYOTA
(0.00o)
--~ OLDWRECK
I (o .0 0 1 )
--> CHEVY
(0.000)
> --> HONDA
(o.000
---> TOYOTA
(0 .0 0 o )
OLDWRECK
I (0 .o 0 0 )
--> CHEVY
(0 .o 0 0 )
-~ HONDA
(0.001)
--~ TOYOTA
(o .o o l)
PRIORITIES
TOYOTA
~.142)
HONDA
(0.115)
CHEVY
(0.166)
OLDWRECK
~. 576)
P R I O R I T I E S
TOYOTA
(0.408)
HONDA
(0.345)
CHEVY
(0.197)
OLDWRECK
(0. 049)
F i g u r e 2. T h e c a t a s t r o p h e h i e r a r c h y
T.L. Saaty / The AHP: How to make a decision 25
al t ernat i ves some cat ast r ophi c ones. Thi s t ype of
t hi nki ng woul d appl y in hi erarchi es where a real
wr ong choi ce is ext r emel y undesi r abl e and costly.
We can also speak of chaos in t he AHP: a
si t uat i on where t he possi bi l i t y of exert i ng cont rol
by creat i ng a hi er ar chy and set t i ng j udgment no
l onger exists, for it is not clear what t akes prece-
dence over what . Usual l y cat ast r ophe pr oduces
chaos. It is possi bl e to r epr esent bot h cat ast r ophe
and chaos in the cont i nuous setting of the AHP.
Bot h cat ast r ophe and chaos are relative. A rev-
ol ut i on may be r egar ded as an undesi rabl e
cat ast r ophe t hat upr oot s a society or as a neces-
sary ki nd of act i on to pr oduce a desi red end. I n
pl anni ng, st rong out - of - t he- or di nar y act i on may
be crucial for affect i ng change.
A si mpl e i l l ust rat i on of how to r epr esent a
cat ast r ophe is given in Fi gure 2. An i ndi vi dual
buyi ng a car makes an i nnocent choi ce by assum-
ing t hat nor mal condi t i ons will prevai l over acci-
dent s in t he rat i o of 0.99 to 0.01. He chooses a
nice new Toyot a, al t hough he knows t hat t here is
a chance t hat an acci dent can happen. I f he were
to buy the car under the assumpt i on of a hi gh
l i kel i hood of an acci dent , 0.99 to 0.01, and if he
were to act in his best self interest, he woul d
choose an old wreck to buy. One answer to this
di l emma is nei t her to buy the old wreck nor the
Toyot a, but to buy a fairly good used car. But
mos t of us are idealists who do not t hi nk t hat
acci dent s will happen to us, and so we buy new
cars.
11. What affects rank [ l l l
Al t hough in cat ast r ophes t here is a sudden shift
in rank, due to a change in the i mpor t ance of the
criteria, what happens t o t he r ank of the al t erna-
tives in the mor e mundane event t hat their num-
ber is changed by addi ng new ones or del et i ng old
ones? The t r adi t i onal rule is t hat r ank reversal is
not accept abl e if, gi ven t hat t he al t ernat i ves t hem-
selves are i ndependent of each ot her, a new al t er-
nat i ve does not i nt r oduce a new cri t eri on or change
t he weights of t he existing criteria. We t end to
t r eat r ank in a possessi ve manner by somet i mes
insisting t hat it st ay the same no mat t er what logic
says. The absol ut e mode of meas ur ement of the
AHP compl i es wi t h this nor mat i ve i ncl i nat i on, but
the rel at i ve mode of meas ur ement does not , be-
cause of the dependence of t he meas ur ement s of
the al t ernat i ves on each ot her. However , rel at i ve
meas ur ement wi l l pr eser ve r ank wi t h respect to a
s i n g l e c r i t e r i on when t he compar i s ons are con-
sistent. Mos t peopl e under s t and t he dependence
of al t ernat i ves in light of t he not i ons of scarci t y
and abundance di scussed earlier. Ther e is no need
to i mpr ovi se not i ons of rel evant and i rrel evant
al t ernat i ves, as is done in utility t heory, because
wi t h rel at i ve meas ur ement ever yt hi ng bei ng com-
par ed is by defi ni t i on rel evant , Ut i l i t y t heor y is
obsessed wi t h t he reversal of r ank because in t hat
t heory it can happen even wi t h respect to a single
criterion. Thi s is a phe nome non t hat is st rongl y
count er i nt ui t i ve and can never be made mat he-
mat i cal l y right. Ut i l i t y theorists, however, t ry to
make it right by phi l osophi cal ar gument s about
what is or is not a rel evant al t ernat i ve.
12. Summary of principles
The AHP generat es rel at i ve rat i o scales of
measur ement . The meas ur ement s of a set of ob-
j ect s on a st andar d scale can be conver t ed to
rel at i ve scale meas ur ement s t hr ough nor mal i za-
tion. Onl y in a very l ocal i zed way can a relative
set of meas ur ement s have a unit, obt ai ned by
di vi di ng the ent i re set by the smal l est measur e-
ment . The nor mal i zat i on and composi t i on of
wei ght s of al t er nat i ve wi t h respect to mor e t han a
single cri t eri on measur ed on the same st andar d
scale l eads to nonsensi cal number s, because nor-
mal i zi ng separ at e sets of number s dest roys the
l i near rel at i on among t hem. The wei ght s must first
be compos ed with respect t o all such cri t eri a and
t hen nor mal i zed for AHP use. We can i nt er pr et
such compos i t i on as we di d in Section 8 as a
special ki nd of wei ght i ng of the par t i cul ar criteria.
Thus, the AHP, wi t h its rel at i ve meas ur ement
offers no gui de on t he out come of mani pul at i ons
based on combi ni ng di fferent measur ement s f r om
a st andar d scale such as a cri t eri on of benefi t s and
a cri t eri on of costs, bot h measur ed in dollars, and
used to select a best al t ernat i ve.
I f we do not insist t hat the l i neari t y of a scale
needs to be pr eser ved (an old habi t f r om when we
di d not have an effect i ve way to i nt er pr et the
i nf or mat i on cont ent of readi ngs f r om a st andar d
scale), we can t hen t reat every cri t eri on as an
i nt angi bl e. I n t hat case we must bear in mi nd t hat
26 T.L. Saaty / The AHP: How to make a decision
t he wei ght s of t he c r i t e r i a d o n o t de r i ve f r om s ome
u n d e r l y i n g s t a n d a r d scal e. I f t he y mu s t d e p e n d on
s uch a scal e, we a r e b a c k t o t he ne e d t o c o mp o s e
b e f o r e n o r ma l i z a t i o n .
The mo r a l is t ha t we a r e s o me t i me s l ed i nt o
d e v e l o p i n g b l i n d e x p e c t a t i o n s f or t ha t t o whi c h we
a r e a c c u s t o me d out of ha bi t , a n d not ne c e s s a r i l y
b e c a u s e i t s t r ut h i s s o me t h i n g wr i t t e n i n gr a ni t e .
We bel i eve t ha t o u r own t e mp e r e d u n d e r s t a n d i n g
s h o u l d p r o d u c e cl os er r es ul t s t o e xpe r i e nc e t h a n
s i mp l y f ol l owi ng t r a d i t i o n , whi c h ha s p o s s i b l y
r u t t e d our t hi nki ng, a n d i n d u c e d us t o f or e go
c h a n g e i n s ear ch of b e t t e r wa ys t ha t gi ve b e t t e r
ans wer s .
References
[1] Eco, U., A Theory of Semiotics, First Midland Book
Edition, Indiana University Press, IN, 1976.
[2] Forman, E., and Saaty, T., Expert Choice Software
Package for I BM PC, Expert Choice, Inc., Pittsburgh, PA
1983-1990.
[3] Harker, P. T. (ed.), "Special Issue on The Analytic
Hierarchy Process", Socio-Economic Planning Sciences
20/6 (1986).
[4] Miller, G.A., "The magical number seven, plus or minus
two: some limits on our capacity for processing informa-
tion", The Psychological Review 63 (1956) 81-97.
[5] Morris, C.W., Foundation of the Theory of Signs, Interna-
tional Encyclopedia of Unified Science, Vols. I and II:
Foundations of the Unity of Science, Vol. 1, No. 2,
University of Chicago Press, 1938.
[6] Saaty, T.L., Decision Making for Leaders: The Analytic
Hierarchy Process for Decisions in a Complex World, RWS
Publications, Pittsburgh, PA, 1986; Original version pub-
lished by Lifetime Learning Publications, 1982.
[7] Saaty, T.L., Multicriteria Decision Making: The Analytic
Hierarchy Process, 1988; Revised and published by the
author; Original version published by McGraw-Hill, New
York, 1980.
[8] Saaty, T.L., "Scaling method for priorities in hierarchical
structures", Journal of Mathematical Psychology 15/3
(1977) 234-281.
[9] Saaty, T.L., "A note on the AHP and expected value
theory", Socio-Economic Planning Sciences 20/6 (1986)
397-398.
[10] Saaty, T.L., and Kearns, K.P., Analytical Planning: The
Organization of Systems, International Series in Modern
Applied Mathematics and Computer Science, Vol. 7, Per-
gamon Press, New York, 1985.
[11] Saaty, T.L., and Vargas, L.G., "Inconsistency and rank
preservation", Journal of Mathematical Psychology 28/2
(1984).
[12] Vargas, L.G., "Reciprocal matrices with random coeffi-
cients", Mathematical Modelling 3 (1982) 69-81.
[13] Vargas, L.G. (ed.), "Special Issue on The Analytic
Hierarchy Process", Mathematical Modelling 9/ 3- 5
(1987).
[14] Wilkinson, J.H., The Algebraic Eigenvalue Problem,
Clarendon Press, Oxford, 1965.
[15] Zahedi, F., "The analytic hierarchy process - A survey of
the method and its applications", Interfaces 16/4 (1986).