Professional Documents
Culture Documents
Digital Image Procesing
Uploaded by
Amritpal SinghOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Digital Image Procesing
Uploaded by
Amritpal SinghCopyright:
Available Formats
Digital Image Procesing
Discrete Walsh Trasform (DWT) in Image Processing
Discrete Hadamard Trasform (DHT) in Image Processing
DR TANIA STATHAKI
READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING
IMPERIAL COLLEGE LONDON
1-D Walsh Transform
This transform is slightly different from the ones
you have met so far!
Suppose we have a function f ( x), x 0,, N 1,
where N 2 n.
We use binary representation for x and u .
We need n bits to represent them.
x10 bn 1 ( x)b0 ( x) 2
Example: 1-D Walsh Transform
Suppose f ( x) has N 8 samples.
In that case n 3 since N 2 n.
Consider f (6) :
x10 6 x2 110 b0 (6) 0, b1 (6) 1, b2 (6) 1
1-D Walsh Transform
We define now the 1-D Walsh transform as follows:
1 N 1
n1
bi ( x )bn1i ( u )
W (u ) f ( x) (1)
N x 0
i 0
The above is equivalent to:
n1
bi ( x )bn1i (u )
1 N 1
W (u ) f ( x)(1) i1
N x 0
The transform kernel values are obtained from:
1
T (u, x) T ( x, u )
N
n1
bi ( x ) bn1i ( u )
bi ( x ) bn1i ( u )
i 1
(
1
)
1
)
i 0
N
n 1
Therefore, the array formed by the Walsh matrix is a real symmetric
matrix. It is easily shown that it has orthogonal columns and rows.
1-D Walsh Transform
We would like to write the Walsh transform in matrix form.
We define the vectors
f f (0)
f (1) f ( N 1)
W W (0) W (1) W ( N 1)
The Walsh transform can be written in matrix form
W T f
As mentioned in previous slide, matrix T is a real, symmetric matrix
with orthogonal columns and rows. We can easily show that it is
unitary and therefore:
T 1 N T T N T , N is thesize of thesignal
1-D Inverse Walsh Transform
Base on the last equation of the previous slide we can show that the
Inverse Walsh transform is almost identical to the forward transform!
n1
f ( x) W (u ) (1)bi ( x )bn1i (u )
x 0
i 0
N 1
The above is again equivalent to
N 1
n1
bi ( x )bn1i (u )
f ( x) W (u )(1) i1
x 0
The array formed by the inverse Walsh matrix is identical to the one
formed by the forward Walsh matrix apart from a multiplicative factor
N.
2-D Walsh Transform
We define now the 2-D Walsh transform as a straightforward
extension of the 1-D transform:
1 N 1 N 1
n1
W (u, v) f ( x, y) (1)bi ( x )bn1i (u )bi ( y )bn1i (v )
N x 0 y 0
i 0
The above is equivalent to:
n1
(bi ( x )bn1i (u )bi ( x )bn1i (u ))
1 N 1 N 1
W (u, v) f ( x, y )(1) i1
N x 0 y 0
2-D Inverse Walsh Transform
We define now the Inverse 2-D Walsh transform. It is identical to the
forward 2-D Walsh transform!
1 N 1 N 1
n1
bi ( x ) bn1i ( u ) bi ( y ) bn1i ( v )
f ( x, y) W (u, v) (1)
N x 0 y 0
i 0
The above is equivalent to:
n1
(bi ( x )bn1i (u )bi ( x )bn1i (u ))
1 N 1 N 1
f ( x, y ) W (u, v)(1) i1
N x 0 y 0
Implementation of the 2-D Walsh Transform
The 2-D Walsh transform is separable and
symmetric.
Therefore it can be implemented as a sequence of
two 1-D Walsh transforms, in a fashion similar to that
of the 2-D DFT.
Basis Functions of Walsh Transform
Remember that the Fourier transform is based on trigonometric
terms.
The Walsh transform consists of basis functions whose values are
only 1 and -1.
They have the form of square waves.
These functions can be implemented more efficiently in a digital
environment than the exponential basis functions of the Fourier
transform.
Kernels of Forward and Inverse Walsh Transform
For 1-D signals the forward and inverse Walsh kernels
differ only in a constant multiplicative factor of N .
This is because the array formed by the kernels is a
symmetric matrix having orthogonal rows and columns, so
its inverse array is the same as the array itself!
In 2-D signals the forward and inverse Walsh kernels are
identical!
The Concept of Sequency
The concept of frequency exists also in Walsh transform
basis functions.
We can think of frequency as the number of zero
crossings or the number of transitions in a basis vector
and we call this number sequency.
The Walsh transform exhibits the property of energy
compaction as all the transforms that we are currently
studying. (why?)
Computation of the Walsh Transform
For the fast computation of the Walsh transform
there exists an algorithm called Fast Walsh
Transform (FWT).
This is a straightforward modification of the FFT.
Advise any introductory book for your own interest.
2-D Hadamard Transform
We define now the 2-D Hadamard transform. It is similar to the 2-D
Walsh transform.
1 N 1 N 1
n1
bi ( x ) bi (u ) bi ( y )bi ( v )
H (u, v) f ( x, y) (1)
N x 0 y 0
i 0
The above is equivalent to:
n1
(bi ( x )bi (u ) bi ( x )bi (u ))
1 N 1 N 1
H (u, v) f ( x, y )(1) i1
N x 0 y 0
2-D Inverse Hadamard Transform
We define now the Inverse 2-D Hadamard transform. It is identical to
the forward 2-D Hadamard transform.
1 N 1 N 1
n1
bi ( x ) bi (u ) bi ( y )bi ( v )
f ( x, y) H (u, v) (1)
N x 0 y 0
i 0
The above is equivalent to:
n1
(bi ( x )bi (u ) bi ( x )bi (u ))
1 N 1 N 1
f ( x, y) H (u, v)(1) i1
N x 0 y 0
Properties of the Hadamard Transform
Most of the comments made for Walsh transform are valid here.
The Hadamard transform differs from the Walsh transform only in the
order of basis functions. The order of basis functions of the Hadamard
transform does not allow the fast computation of it by using a
straightforward modification of the FFT.
The Hadamard transform does not posses the property of energy
compaction!
Based on the above, WHY USE IT THEN???
Recursive Relationship of the Hadamard Transform
An important property of Hadamard transform is that,
letting H N represent the Hadamard matrix of order N
the recursive relationsh ip holds :
H 2N
H N
H N
HN
H N
Therefore, starting from a small Hadamard matrix
we can compute a Hadamard matrix of any size.
This is a good reason to use the Hadamard transform!
And more on good properties
An extended version of the Hadamard transform is the
ordered Hadamard transform for which a fast algorithm
called Fast Hadamard Transform (FHT) can be applied.
The ordered Hadamard transform DOES exhibit the
property of energy compaction!
Images of 1-D Hadamard matrices
More images of 1-D Hadamard matrices
8x8 Hadamard matrix (non-ordered)
8x8 Hadamard matrix (ordered)
16x16 Hadamard matrix (non-ordered)
16x16 Hadamard matrix (ordered)
More images of 1-D Hadamard matrices
32x32 Hadamard matrix (non-ordered)
32x32 Hadamard matrix (ordered)
64x64 Hadamard matrix (non-ordered)
64x64 Hadamard matrix (ordered)
Superiority of DCT in terms of energy compaction in comparison with Hadamard
Experiment
The 256x256 DCT matrix
Display of a logarithmic function
of the DCT of cameraman
The cumulative transform
energy sequences
Non-ordered and ordered Hadamard
The ordered Hadamard Transform
of cameraman
The cumulative transform energy sequences
The non-ordered Hadamard Transform
of cameraman
The sequency of transform
as a function of the sample index
Question: In the bottom figures which of the two transforms is related to each curve?
2-D Walsh Basis Functions
0
2-D Walsh basis
functions for 4x4
images.
x,y,u,v are between 0
and 3.
For a fixed (u,v) we
plot the 4x4 functions
T(x,y,u,v)
You might also like
- L10 - Walsh & Hadamard TransformsDocument25 pagesL10 - Walsh & Hadamard TransformsRakesh Inani100% (1)
- L10 - Walsh & Hadamard +haar TransformsDocument37 pagesL10 - Walsh & Hadamard +haar TransformsramadeviNo ratings yet
- Digital Image Processing - Advanced CourseDocument240 pagesDigital Image Processing - Advanced CoursesaravisaNo ratings yet
- Wavelet Transform Theory ExplainedDocument29 pagesWavelet Transform Theory ExplainedIrfan ShaikNo ratings yet
- Inverse DWTDocument18 pagesInverse DWTSafa_AlrawiNo ratings yet
- Mat Lab ProgramsDocument234 pagesMat Lab ProgramsAhmed HwaidiNo ratings yet
- Discrete Time DomainDocument28 pagesDiscrete Time DomainfurqanNo ratings yet
- Why z-Transform Generalizes Fourier TransformDocument57 pagesWhy z-Transform Generalizes Fourier TransformDe BuNo ratings yet
- Fourier Transform: Naveen SihagDocument54 pagesFourier Transform: Naveen SihagDr. M. Karthigai Pandian Asso Prof ICENo ratings yet
- DSP II Math BackgroundDocument21 pagesDSP II Math BackgroundraviNo ratings yet
- Fourier Transforms and Image ProcessingDocument60 pagesFourier Transforms and Image ProcessingPillalamarri LaxmanNo ratings yet
- Cal1 Chapter 2Document92 pagesCal1 Chapter 2Vân Anh Nguyễn NgọcNo ratings yet
- ROC Z TransformDocument15 pagesROC Z TransformMohammad Gulam Ahamad0% (1)
- Z TransformDocument15 pagesZ TransformSN DhakerNo ratings yet
- Digital Image Processing (Chapter 4)Document62 pagesDigital Image Processing (Chapter 4)Md.Nazmul Abdal Shourov100% (1)
- Moving into the Frequency DomainDocument71 pagesMoving into the Frequency DomainHafid ScooteristNo ratings yet
- Z TransformDocument15 pagesZ TransformSureshKumarNo ratings yet
- EE6403 Discrete Time Systems and Signal Processing NotesDocument20 pagesEE6403 Discrete Time Systems and Signal Processing NotesishuNo ratings yet
- Gradient Descent Based LearnersDocument11 pagesGradient Descent Based LearnerssandtNo ratings yet
- Example - Haar Wavelets: L D D DDocument35 pagesExample - Haar Wavelets: L D D DashoksakjnijNo ratings yet
- Digital Image Processing Question & AnswersDocument14 pagesDigital Image Processing Question & AnswersSuresh ThallapelliNo ratings yet
- Week 6 - Z-TransformDocument15 pagesWeek 6 - Z-TransformRalph Ian CaingcoyNo ratings yet
- JKLDocument14 pagesJKLnono mauritiusNo ratings yet
- Approximating Financial Time Series with WaveletsDocument14 pagesApproximating Financial Time Series with Waveletsnono mauritiusNo ratings yet
- Lab 10-Descrete Fourier Transform and Circular ConvolutionDocument8 pagesLab 10-Descrete Fourier Transform and Circular ConvolutionAleena QureshiNo ratings yet
- Digital Signal & Image Processing B Option - 8 Lectures: Stephen Roberts Sjrob@robots - Ox.ac - UkDocument172 pagesDigital Signal & Image Processing B Option - 8 Lectures: Stephen Roberts Sjrob@robots - Ox.ac - UkDotressus MmokNo ratings yet
- Dip S8ece Module2Document67 pagesDip S8ece Module2Neeraja JohnNo ratings yet
- Z-Transform: Signal Processing IIDocument19 pagesZ-Transform: Signal Processing IIChrispinus ChristianNo ratings yet
- BAB 2. FourierDocument31 pagesBAB 2. FourierExioraNo ratings yet
- Digital Image Processing Unit-2Document6 pagesDigital Image Processing Unit-2Pritesh GuptaNo ratings yet
- Lecture2 ProbablityDocument27 pagesLecture2 Probablityatifjaved91No ratings yet
- HadamandDocument25 pagesHadamandullisrinuNo ratings yet
- Topic5 Linear TransformationsDocument25 pagesTopic5 Linear TransformationsFilipus Boby Setiawan BudimanNo ratings yet
- METO630-Tangborn Wavelet 2009Document29 pagesMETO630-Tangborn Wavelet 2009Rajnish RajNo ratings yet
- Chapter 4 &5Document52 pagesChapter 4 &5Ken MutaiNo ratings yet
- Transform CodingDocument27 pagesTransform CodingvilavanadonisNo ratings yet
- 2) Image Transforms Part 2Document74 pages2) Image Transforms Part 2Deepak GawaliNo ratings yet
- Plugin HilberttransformsDocument13 pagesPlugin Hilberttransformsabnou_223943920No ratings yet
- 2 Transform Coding - KLT - DiscrietDocument17 pages2 Transform Coding - KLT - DiscrietABHISHEK BNo ratings yet
- Lec28 DCTDocument14 pagesLec28 DCTYaser Ali Tariq100% (1)
- Robot Arms, Hands: Kinematics ExplainedDocument59 pagesRobot Arms, Hands: Kinematics Explainedjose_balcazar89No ratings yet
- Image Enhancement Frequency Domain TechniquesDocument61 pagesImage Enhancement Frequency Domain Techniquessasindhur rNo ratings yet
- The DWT for Image CompressionDocument31 pagesThe DWT for Image CompressionEmir BuzaNo ratings yet
- Digital Signal Processing Important Two Mark Questions With AnswersDocument15 pagesDigital Signal Processing Important Two Mark Questions With AnswerssaiNo ratings yet
- Z Transform PropertiesDocument43 pagesZ Transform PropertiesSalman KhanNo ratings yet
- Sistel - 02 - FourierDocument31 pagesSistel - 02 - FourierRivaldi MhsNo ratings yet
- c2 PDFDocument10 pagesc2 PDFChristos DedesNo ratings yet
- Lecture5 Data CompressionDocument20 pagesLecture5 Data CompressionAbdo ANNo ratings yet
- CS474 Wavelets Chapter 7 SummaryDocument109 pagesCS474 Wavelets Chapter 7 SummarylavanyachezhiyanNo ratings yet
- Summary Dig FiltDocument21 pagesSummary Dig FiltWill BlackNo ratings yet
- Frequency DomainDocument71 pagesFrequency Domainsanju_arora19No ratings yet
- DSP Lab Expt 4 Manual EECE GITAM-1-6Document6 pagesDSP Lab Expt 4 Manual EECE GITAM-1-6gowri thumburNo ratings yet
- Frequency Domain ProcessingDocument42 pagesFrequency Domain ProcessingInJune YeoNo ratings yet
- U2 P3 Fourier Transform April23Document37 pagesU2 P3 Fourier Transform April23Raul xddNo ratings yet
- WT Lecture 8Document15 pagesWT Lecture 8Pushpa Mohan RajNo ratings yet
- Fundamentals of the Discrete Haar Wavelet TransformDocument19 pagesFundamentals of the Discrete Haar Wavelet TransformsoumensahilNo ratings yet
- Recursive Least-Squares Adaptive Filters: Dr. Yogananda IsukapalliDocument28 pagesRecursive Least-Squares Adaptive Filters: Dr. Yogananda IsukapalliAkilesh MDNo ratings yet
- Low Pass and High Pass FiltersDocument6 pagesLow Pass and High Pass Filterssrc0108No ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Raj Ender 2014Document6 pagesRaj Ender 2014Amritpal SinghNo ratings yet
- DC Machines Lab ManualDocument153 pagesDC Machines Lab ManualdaluNo ratings yet
- Australasian Physical & Engineering Sciences in MedicineDocument29 pagesAustralasian Physical & Engineering Sciences in MedicineAmritpal SinghNo ratings yet
- Revised FractalDocument21 pagesRevised FractalAmritpal SinghNo ratings yet
- ECG FilteringDocument25 pagesECG FilteringkirangreatloverNo ratings yet
- 63796670Document9 pages63796670Amritpal SinghNo ratings yet
- Coherence, Phase and Cross-Correlation: X, Y S T S T X, Y X, Y Y, X X, Y X, YDocument6 pagesCoherence, Phase and Cross-Correlation: X, Y S T S T X, Y X, Y Y, X X, Y X, YAmritpal SinghNo ratings yet
- MỘT SỐ HÀM THƯ VIỆN THÔNG DỤNGDocument25 pagesMỘT SỐ HÀM THƯ VIỆN THÔNG DỤNGtinpt09214No ratings yet
- Exp 5-SteamPowerPlantDocument11 pagesExp 5-SteamPowerPlantFirst LastNo ratings yet
- Assignment No.3 Bolted JointsDocument6 pagesAssignment No.3 Bolted JointsYash SahuNo ratings yet
- Flow MeterDocument9 pagesFlow MeterShin BoNo ratings yet
- Instantaneous Waterhammer EquationDocument10 pagesInstantaneous Waterhammer EquationkiranNo ratings yet
- Managing Economies of Scale in Supply ChainsDocument25 pagesManaging Economies of Scale in Supply ChainsWei JunNo ratings yet
- Fire Strength Performance ofDocument3 pagesFire Strength Performance ofMarimuthu KannimuthuNo ratings yet
- Focal Points: Basic Optics, Chapter 4Document47 pagesFocal Points: Basic Optics, Chapter 4PAM ALVARADONo ratings yet
- Ska611hdgdc (210) (12BB) (2384×1303×35) (680 700)Document2 pagesSka611hdgdc (210) (12BB) (2384×1303×35) (680 700)Marko Maky ZivkovicNo ratings yet
- Selection of Dryers I - IndiaDocument38 pagesSelection of Dryers I - Indiasilvership2291100% (1)
- Kalman Filter Tutorial - PresentationDocument65 pagesKalman Filter Tutorial - Presentationcarlazar100% (2)
- Primary Reformer TubesDocument10 pagesPrimary Reformer TubesAhmed ELmlahyNo ratings yet
- P18 Probability in The CourtroomDocument14 pagesP18 Probability in The CourtroomYehiaNo ratings yet
- 913-2174-01 - Ibypass VHD User Guide Version 1.5 - Revh - VanphDocument218 pages913-2174-01 - Ibypass VHD User Guide Version 1.5 - Revh - Vanphpham hai van100% (1)
- D200801 Slope and Offset Adjustment For A Pressure SensorDocument4 pagesD200801 Slope and Offset Adjustment For A Pressure SensorBrian McMorrisNo ratings yet
- SD Revenue Account Determination SetupDocument10 pagesSD Revenue Account Determination SetupkarthikbjNo ratings yet
- Lab 8 - LP Modeling and Simplex MethodDocument8 pagesLab 8 - LP Modeling and Simplex MethodHemil ShahNo ratings yet
- The Gist of NCERT General Science PDFDocument148 pagesThe Gist of NCERT General Science PDFSatyajitSahooNo ratings yet
- Data Communication & Computer NetworksDocument32 pagesData Communication & Computer NetworksMuhammad NadeemNo ratings yet
- Cot 2018-2019Document11 pagesCot 2018-2019Crush Na Crush KitaNo ratings yet
- 03a IGCSE Maths 4MB1 Paper 2R - January 2020 Examination PaperDocument32 pages03a IGCSE Maths 4MB1 Paper 2R - January 2020 Examination PaperMehwish ArifNo ratings yet
- Novel Proteinaceous Infectious Particles Cause ScrapieDocument10 pagesNovel Proteinaceous Infectious Particles Cause ScrapieMikey HaveyNo ratings yet
- Trafo 40 Mva PDFDocument719 pagesTrafo 40 Mva PDFeug_manu8No ratings yet
- Directions: Answer The Following Question(s) .: A. B. C. D. E. FDocument6 pagesDirections: Answer The Following Question(s) .: A. B. C. D. E. FdiamondtressNo ratings yet
- Vitamins With Minerals Oral PowderDocument8 pagesVitamins With Minerals Oral PowderWH PANDWNo ratings yet
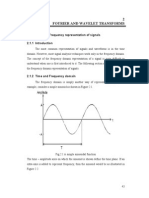
- 2 Fourier and Wavelet Transforms: 2.1. Time and Frequency Representation of SignalsDocument25 pages2 Fourier and Wavelet Transforms: 2.1. Time and Frequency Representation of SignalszvjpNo ratings yet
- R Fulltext01Document136 pagesR Fulltext01vhj gbhjNo ratings yet
- EEE415 Digital Image Processing: Frequency Domain FilteringDocument50 pagesEEE415 Digital Image Processing: Frequency Domain FilteringFAISAL NAWABNo ratings yet
- C - Brim - 1909 80 - QDocument40 pagesC - Brim - 1909 80 - Qmanohar rathodNo ratings yet