Professional Documents
Culture Documents
Cavitation Notes
Uploaded by
FIRDAUS BIN MAHAMADOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Cavitation Notes
Uploaded by
FIRDAUS BIN MAHAMADCopyright:
Available Formats
Cavitation Notes
p 0 = uniform_stream_total_pressure V0 = uniform_stream_velocity q= 1 2
2
p 1 = pressure_at_arbitrary_point V1 = velocity_at_arbitrary_point
ref: PNA pages 181-183 handout
V0 = dynamic_or_stagnation_or_ram_pressure 1 V0 = constant 2
1 2 V0
2 2
p0 +
Bernoulli
p 1 := constant 1 2 V1
2
p 0 := constant
for propeller immersion, measured at radius r, minimum p 0 is obtained from ... p 0 = p a + gh gr p a = atmosphere
h = shaft_centerline_immersion
gr V0 estimated as (VA^2+(*r)^2)0.5 define: L = local_cavitation_number = accounts for minimum when r vertical up if p1 => pv = vapor pressure, cavitation occurs p a + gh gr p v
2 2 2 V + r 2 A
and if pressure REDUCTION / q >= L cavitation occurs
early criteria (Barnaby) suggested limiting average thrust per unit area to certain values (76.7 kN/m2 = 10.8 psi) for tip immersion of 11 in increasing by 0.35 psi (unit conversions don't match up) 76.7 kN m
2
= 11.124 psi
earlier PNA (1967) stated Barnaby suggested 11.25 psi
can calculate pressure distributions around blade so can calculate local cavitation situation early in propeller design, want blade area to avoid cavitation (more blade area, less pressure
per unit area for given thrust)
Burrill ((1943) "Developments in Propeller Design and Manufacture for Merchant Ships",
Trans. Institute of Marine Engineers, London, Vol. 55) proposed guidance as follows:
limit thrust (coefficient) to a certain value depending on cavitation number at the 0.7 radius
c = coefficient_expressing_mean_loading_on_blades
T = thrust AP = projected_area = water_density VR = relative_velocity_of_water_at_0_7_radius AP AD = 1.067 0.229 P D from Taylor S & P page 91 P/D from 0.6 to 2.0 elliptical bladed prop, hub = 0.2 D c = 1 2
T AP
VR
can estimate projected area from
and as usual ...
T=
PE ( 1 t) V
PD D (1 t) V
PD = delivered_power PE = effective_power
RT = T( 1 t) PE = RTV
D = quasi_propulsive_coefficient = this parameter is plotted versus
3 kg
PE PD
= H R o
H =
1t 1w
0.7 slug
ft
3
cavitation number at 0.7*r using relative velocity at 0.7*r and pressure at CENTERLINE
:= 1.0259 10
= 1.99057
0.7 =
p 0 + gh p v 1 2 VA + ( 0.7 n D)
188.2 + 19.62 h VA + 4.836 ( n D)
2 2
m VA = sec D=m
h=m
1
n = sec
units in PNA (61) approximation SI pv apparently ~ 0.69 psi (90 degF)
0.7 =
2026 + 64.4 VA + 4.836( n D)
2 2
in US units
Carmichael correlation
C :=
c + 0.3064 0.523 0.0305
0.2
0.2
C = cavitation % at 0.7 radius as above (centerline immersion)
c as above
0.0174
example numbers := 0.4 c := 0.2 C :=
0.2
c + 0.3064 0.523 0.0305
0.2
for C <= 25 (%) or so C = 8.88 % cavitation
0.0174
:= 0.1 , 0.11 .. 2
or ...
c( C , ) := C 0.0305
T
0.2
0.0174 + 0.523
0.2
0.3064
see plot below
this can be carried further into ...
c =
AP
1 2
VR
= C 0.0305
0.2
0.0174 + 0.523
0.2
0.3064
AP = 1
VR C 0.0305 2
2
T
0.2
0.0174 + 0.523
0.2
0.3064
Ap = minimum_area_for_specified_cavitation
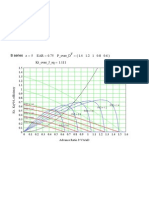
c(30, ) c(20, ) c(10, ) c(5, ) c(2, )
0.1 0.1
Carmichael correlation valid only for C <= 25 %. 30 % shown to indicate over estimates compared with fig 45 page 182 of PNA for example from prop_design_notes T := 278000lbf n := 218rpm D := 15ft P_over_D := 0.8 p 0 + gh p v 1 2 := VA + ( 0.7nD) 188.2 + 19.62 h VA + 4.836(n D)
2 2
derived above p 0 = 14.696 psi p v = 0.694 psi
rpm := min
kt := 1.688
ft s
VA := 14kt
h := 10ft
0.7 r =
m VA = sec
D=m
h=m
n = sec
p 0 + gh p v
2 2 VA + ( 0.7nD) 2
m VA = 7.203 D = 4.572 m s 188.2 + 19.62 3.048 7.203 + 4.836( 3.633 4.572)
2 2
h = 3.048 m n = 3.633
1 s
= 0.179
= 0.179 using SI approximation
2 0.5
consider % cavitation in steps of 5%
C := 5 , 10 .. 25
VR := VA + ( 0.7n D)
2
m VR = 37.234 s
AP( C) := 1 2
0.2 0.2 VR C 0.0305 0.0174 + 0.523 0.3064 2
AP AD
= 1.067 0.229
P D
assume AD ~ AE
AP( C) AE( C) := 1.067 0.229 P_over_D cavitation % C =
5 10 15 20 25
AP( C) =
20.367 16.333 13.632 11.698 10.245
estimated minimum EAR to avoid AE( C)
AE( C) = =
2 D 23.045 2 m 4 18.48
15.425 13.236 11.592 1.404 1.126 0.94 0.806 0.706
supercavitating c to the left. very low cavitation % is 100 h = 3.048 m D = 4.572 m m VA = 7.203 s m VA := 10 s 0.7 r = p 0 + gh p v
2 2 VA + ( 0.7nD) 2
n = 218
1 min 0.7nD = 36.531 0.7nD = 167.573
m s m s
n := 1000rpm
:=
p 0 + gh p v 1 2 VA + ( 0.7nD)
= 8.8 10
to avoid 25% cavitation c( C , ) := C 0.0305
C := 25 0.0174 + 0.523
0.2
0.2
0.3064
c( C , ) = 0.243
off the scale hence supercavitating propellers correlation not valid but trend is ok
You might also like
- The 100 - Ranking of Most Influential People in History - Michael Hart Citadel Press 1992Document591 pagesThe 100 - Ranking of Most Influential People in History - Michael Hart Citadel Press 1992jasimnddNo ratings yet
- Miata Wiring NA8 DiagramDocument65 pagesMiata Wiring NA8 DiagramseanNo ratings yet
- Theory of SuperconductivityDocument135 pagesTheory of SuperconductivityRenjith Raveendran PillaiNo ratings yet
- Ultrasonics For First Year .B.Tech. StudentsDocument9 pagesUltrasonics For First Year .B.Tech. StudentsSuryasrikar Peruri100% (1)
- Practical Organic ChemistryDocument598 pagesPractical Organic ChemistryGerardo Estrada99% (127)
- Underwater Laser Micromachining of Silicon in Pressurized EnvironmentDocument9 pagesUnderwater Laser Micromachining of Silicon in Pressurized Environmentসুহাস মন্ডলNo ratings yet
- Using KT and KQ For DesignDocument7 pagesUsing KT and KQ For DesignFIRDAUS BIN MAHAMAD100% (2)
- Plantas Con Madre Plants That Teach and PDFDocument15 pagesPlantas Con Madre Plants That Teach and PDFJetNo ratings yet
- PDFDocument1 pagePDFJaime Arroyo0% (1)
- Electromagnetic Induction: (A) Electricity From MagnetismDocument6 pagesElectromagnetic Induction: (A) Electricity From MagnetismGaurav ChopraNo ratings yet
- VASCHE AD ULTRASUONI GB LowDocument16 pagesVASCHE AD ULTRASUONI GB Lowkaka punNo ratings yet
- Application of Ultrasonic Technology For Water andDocument17 pagesApplication of Ultrasonic Technology For Water andMartin DarmasetiawanNo ratings yet
- CPX H Ultrasonic Baths DataDocument2 pagesCPX H Ultrasonic Baths DataRodrigo Morales VeraNo ratings yet
- Ultrasonic Cleaner B200 - Manual PDFDocument1 pageUltrasonic Cleaner B200 - Manual PDFbasiliolikNo ratings yet
- Models - Acdc.capacitor Fringing FieldsDocument16 pagesModels - Acdc.capacitor Fringing FieldsAnonymous pWNBPuMcf100% (1)
- Reliability and AvailablityDocument6 pagesReliability and AvailablityFIRDAUS BIN MAHAMADNo ratings yet
- Models - Aco.piezoacoustic TransducerDocument16 pagesModels - Aco.piezoacoustic TransducerLeuca Bogdan-CostinNo ratings yet
- Electromagnetism Part 4 StudentsDocument16 pagesElectromagnetism Part 4 StudentsSharvinder SinghNo ratings yet
- Sonication From Wikipedia, The Free Encyclopedia: UltrasonicDocument4 pagesSonication From Wikipedia, The Free Encyclopedia: UltrasonicJimmyNo ratings yet
- The Use of Ultrasonic Cleaning in Dairy Industry: How Does It Work?Document3 pagesThe Use of Ultrasonic Cleaning in Dairy Industry: How Does It Work?Vetz clubNo ratings yet
- Introduction To Magnetic CircuitsDocument23 pagesIntroduction To Magnetic Circuitssharad kumarNo ratings yet
- WTS 12 ElectrodynamicsDocument28 pagesWTS 12 ElectrodynamicsTondani100% (1)
- Sfra For Condition Monitoring of Power TransformerDocument3 pagesSfra For Condition Monitoring of Power TransformerSarojakanti SahooNo ratings yet
- COMSOL V4.4 Acoustic-AnalysisDocument162 pagesCOMSOL V4.4 Acoustic-Analysisਸ. ਇੰਦਰਦੀਪ ਸਿੰਘNo ratings yet
- Ef Cacy of Sonically, Ultrasonically Andlaser-Activated Irrigation in Removing Abio Lm-Mimicking Hydrogel From An Isthmus ModelDocument9 pagesEf Cacy of Sonically, Ultrasonically Andlaser-Activated Irrigation in Removing Abio Lm-Mimicking Hydrogel From An Isthmus ModelBenjiNo ratings yet
- Power Inductor Modelling Using Comsol Multi PhysicsDocument10 pagesPower Inductor Modelling Using Comsol Multi PhysicsDinesh Perumalsamy100% (1)
- Liquid Processing CatalogDocument31 pagesLiquid Processing CatalogLina Maria RodriguezNo ratings yet
- Applications of Electromagnetic InductionDocument6 pagesApplications of Electromagnetic InductionLivombo AveloNo ratings yet
- Investigations On A Standing Wave Thermoacoustic RefrigeratorDocument8 pagesInvestigations On A Standing Wave Thermoacoustic RefrigeratorAli AHNo ratings yet
- Ultrasonic Cleaning - Fundamental Theory and Application CTG Clean PDFDocument12 pagesUltrasonic Cleaning - Fundamental Theory and Application CTG Clean PDFMusunuri Ratna TejaNo ratings yet
- The Generation of ElectricityDocument42 pagesThe Generation of ElectricityNorazlin UjangNo ratings yet
- Characterization of Atmospheric Pressure Discharges: R.Barni, S.Zanini, R.Siliprandi, P.Esena, C.RiccardiDocument8 pagesCharacterization of Atmospheric Pressure Discharges: R.Barni, S.Zanini, R.Siliprandi, P.Esena, C.RiccardiRodrigo RamosNo ratings yet
- Application of Hydrodynamic Cavitation ReactorsDocument24 pagesApplication of Hydrodynamic Cavitation ReactorsJeffery TaylorNo ratings yet
- Ultrasonic Assisted Underwater Laser Micromachining of SiliconDocument29 pagesUltrasonic Assisted Underwater Laser Micromachining of SiliconBLACK SABBATHNo ratings yet
- UltrasonicCleaner VWRDocument27 pagesUltrasonicCleaner VWR664214458No ratings yet
- Transmission LineDocument11 pagesTransmission LineDeni RistiantoNo ratings yet
- Models - Rf.conical AntennaDocument16 pagesModels - Rf.conical AntennaMatteo TorinoNo ratings yet
- Acoustic Microbubble Dynamics With Viscous Effects 2016Document10 pagesAcoustic Microbubble Dynamics With Viscous Effects 2016Kawa Mustafa AzizNo ratings yet
- Models - Aco.piezoacoustic TransducerDocument14 pagesModels - Aco.piezoacoustic Transducerkiran kumar kNo ratings yet
- Pressure Control Valve VRCDDocument4 pagesPressure Control Valve VRCDFlavius Oros100% (1)
- Preliminary Design of Amphibious CraftDocument7 pagesPreliminary Design of Amphibious CraftFIRDAUS BIN MAHAMADNo ratings yet
- Editorial WritingDocument38 pagesEditorial WritingMelanie Antonio - Paino100% (1)
- Catalogue - Probe Sonicator - Ultra Autosonic IndiaDocument4 pagesCatalogue - Probe Sonicator - Ultra Autosonic IndiaGirish GuptaNo ratings yet
- Computer-Controlled Sophisticated Ultrasonic Cleaner: H. Muthurajan, H.H. Kumar, and D.K. KharatDocument4 pagesComputer-Controlled Sophisticated Ultrasonic Cleaner: H. Muthurajan, H.H. Kumar, and D.K. KharatNKJemesNo ratings yet
- Project ProposalDocument2 pagesProject Proposalqueen malik80% (5)
- Acdc - DC Motor - Lecture Notes 5Document30 pagesAcdc - DC Motor - Lecture Notes 5Cllyan ReyesNo ratings yet
- Ultra Sonic Bath Instruction Manual (Labcon UBM22) PDFDocument13 pagesUltra Sonic Bath Instruction Manual (Labcon UBM22) PDFilroux100% (2)
- Resonance UnlockedDocument5 pagesResonance UnlockedgjjgNo ratings yet
- To Demonstrate The Process of Cavitations: Group MembersDocument7 pagesTo Demonstrate The Process of Cavitations: Group MembersMansoob BukhariNo ratings yet
- Models - Acdc.capacitor TunableDocument12 pagesModels - Acdc.capacitor TunableAnnuar BrnalNo ratings yet
- Chapter 3: Electrolytic Conductance 3.1. Specific Conductance Specific Conductance Is A Measure of The Electric Current in The Water SampledDocument11 pagesChapter 3: Electrolytic Conductance 3.1. Specific Conductance Specific Conductance Is A Measure of The Electric Current in The Water SampledBùi Hữu ĐứcNo ratings yet
- (Done 5) Mechanical and Chemical Effects On The Frequency of UltrasonicDocument5 pages(Done 5) Mechanical and Chemical Effects On The Frequency of Ultrasonicاشکان صفربالیNo ratings yet
- An Update On Ultrasonic Irrigant ActivationDocument15 pagesAn Update On Ultrasonic Irrigant ActivationkarishmaNo ratings yet
- Computing CapacitanceDocument16 pagesComputing Capacitancepraveeng11100% (1)
- The Influence of The Ultrasonic Intensity On The CleaningDocument5 pagesThe Influence of The Ultrasonic Intensity On The Cleaningernesto fidel aramendiz galindoNo ratings yet
- IsyTech 31-10 - 31-11 - IngleseDocument12 pagesIsyTech 31-10 - 31-11 - InglesedmakaricNo ratings yet
- Ultrasonic InterferometerDocument5 pagesUltrasonic InterferometerRadot ChandraNo ratings yet
- Computational Aeroacoustics An Overview PDFDocument14 pagesComputational Aeroacoustics An Overview PDFVenu MadhavNo ratings yet
- Electron ModelsDocument13 pagesElectron ModelsNooruddin SheikNo ratings yet
- Ultrasonic Waves: 1. Production of UltrasonicsDocument7 pagesUltrasonic Waves: 1. Production of UltrasonicsAmit KumarNo ratings yet
- Isoloop Magnetic CouplerDocument23 pagesIsoloop Magnetic CouplerKarthik Surabathula100% (1)
- Introduction To Electrochemistry: The Scope of ElectrochemistryDocument10 pagesIntroduction To Electrochemistry: The Scope of ElectrochemistrymariaNo ratings yet
- Applications of Ultrasound in Organic SynthesisDocument2 pagesApplications of Ultrasound in Organic SynthesisLav VarmaNo ratings yet
- CavitationDocument12 pagesCavitationVarun Vikram SinghNo ratings yet
- Atomic Structure - Discovery of Subatomic ParticlesDocument6 pagesAtomic Structure - Discovery of Subatomic ParticlesDivyansh DangiNo ratings yet
- Infection Prevention Using Sterelization MethodsDocument42 pagesInfection Prevention Using Sterelization MethodsAliyu NasirNo ratings yet
- Diffraction by Ultrasonic Waves in LiquidDocument5 pagesDiffraction by Ultrasonic Waves in LiquidParmanandaNo ratings yet
- Direct Vs Alternating Current: BelowDocument5 pagesDirect Vs Alternating Current: Belowtgs100No ratings yet
- Assignment 02Document6 pagesAssignment 02Javeria NaseemNo ratings yet
- 02 045 FDSDocument8 pages02 045 FDSJaveria NaseemNo ratings yet
- Waterjet: = patmos + ρ ⋅g⋅d +Document4 pagesWaterjet: = patmos + ρ ⋅g⋅d +FIRDAUS BIN MAHAMADNo ratings yet
- B SeriesDocument1 pageB SeriesFIRDAUS BIN MAHAMADNo ratings yet
- Master Thesis On Smart GridDocument6 pagesMaster Thesis On Smart Gridsandraandersondesmoines100% (2)
- Shot Blasting Machine ApplicationsDocument7 pagesShot Blasting Machine ApplicationsBhavin DesaiNo ratings yet
- Medha Servo Drives Written Exam Pattern Given by KV Sai KIshore (BVRIT-2005-09-ECE)Document2 pagesMedha Servo Drives Written Exam Pattern Given by KV Sai KIshore (BVRIT-2005-09-ECE)Varaprasad KanugulaNo ratings yet
- Directorate of Technical Education, Maharashtra State, MumbaiDocument57 pagesDirectorate of Technical Education, Maharashtra State, MumbaiShubham DahatondeNo ratings yet
- Vacon NX, Non-Regenerative Front End FI9 UD01217B PDFDocument48 pagesVacon NX, Non-Regenerative Front End FI9 UD01217B PDFSilvian IonescuNo ratings yet
- IOM - Rampa Hidráulica - Blue GiantDocument32 pagesIOM - Rampa Hidráulica - Blue GiantPATRICIA HERNANDEZNo ratings yet
- Module 0-Course Orientation: Objectives OutlineDocument2 pagesModule 0-Course Orientation: Objectives OutlineEmmanuel CausonNo ratings yet
- Dashrath Nandan JAVA (Unit2) NotesDocument18 pagesDashrath Nandan JAVA (Unit2) NotesAbhinandan Singh RanaNo ratings yet
- Woldia University: A Non Ideal TransformerDocument24 pagesWoldia University: A Non Ideal TransformerKANDEGAMA H.R. (BET18077)No ratings yet
- Chapter 3 PayrollDocument5 pagesChapter 3 PayrollPheng Tiosen100% (2)
- TMA GuideDocument3 pagesTMA GuideHamshavathini YohoratnamNo ratings yet
- 5 Teacher Induction Program - Module 5Document27 pages5 Teacher Induction Program - Module 5LAZABELLE BAGALLON0% (1)
- Dark Energy Survey DES CollaborationDocument38 pagesDark Energy Survey DES CollaborationgeorgcantorNo ratings yet
- Muhammad Firdaus - A Review of Personal Data Protection Law in IndonesiaDocument7 pagesMuhammad Firdaus - A Review of Personal Data Protection Law in IndonesiaJordan Amadeus SoetowidjojoNo ratings yet
- Module 1 Dynamics of Rigid BodiesDocument11 pagesModule 1 Dynamics of Rigid BodiesBilly Joel DasmariñasNo ratings yet
- Ems Speed Sensor Com MotorDocument24 pagesEms Speed Sensor Com MotorKarina RickenNo ratings yet
- Age and Gender Detection Using Deep Learning: HYDERABAD - 501 510Document11 pagesAge and Gender Detection Using Deep Learning: HYDERABAD - 501 510ShyamkumarBannuNo ratings yet
- EdM 101 - Joan Marie PeliasDocument9 pagesEdM 101 - Joan Marie Peliasjoan marie Pelias100% (1)
- Stellite 6 FinalDocument2 pagesStellite 6 FinalGumersindo MelambesNo ratings yet
- Asian Paints Final v1Document20 pagesAsian Paints Final v1Mukul MundleNo ratings yet
- ShopDrawings - Part 1Document51 pagesShopDrawings - Part 1YapNo ratings yet
- List of Institutions With Ladderized Program Under Eo 358 JULY 2006 - DECEMBER 31, 2007Document216 pagesList of Institutions With Ladderized Program Under Eo 358 JULY 2006 - DECEMBER 31, 2007Jen CalaquiNo ratings yet
- Résumé Emily Martin FullDocument3 pagesRésumé Emily Martin FullEmily MartinNo ratings yet