CHAPTER

Continuous Probability Distributions

n this chapter, we dene continuous probability distributions and describe the most popular ones. We look closely at the normal probability distribution, which is the mainstay of nance theory, risk measures, and performance measuresand its appeal, despite the preponderance of empirical evidence and theoretical arguments that many nancial economic variables do not follow a normal distribution. We postpone until Chapter 7 a discussion of a class of continuous probability distributions, called stable Paretian distributions, which we show in later chapters are more appropriate in many applications in nance.

CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS

If the random variable can take on any possible value within the range of outcomes, then the probability distribution is said to be a continuous random variable.1 When a random variable is either the price of or the return on a nancial asset or an interest rate, the random variable is assumed to be continuous. This means that it is possible to obtain, for example, a price of 95.43231 or 109.34872 and any value in between. In practice, we know that nancial assets are not quoted in such a way. Nevertheless, there is no loss in describing the random variable as continuous and in
1

Precisely, not every random variable taking its values in a subinterval of the real numbers is continuous. The exact definition requires the existence of a density function such as the one that we use later in this chapter to calculate probabilities.

23

Continuous Probability Distributions

29
t

P(X t) = F(t) =

f ( x ) dx

The cumulative distribution function is another way to uniquely characterize an arbitrary probability distribution on the set of real numbers and in Chapter 7 we learn a third possibility, the so-called characteristic function.

THE NORMAL DISTRIBUTION

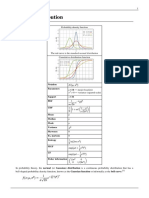
The class of normal distributions is certainly one of the most important probability distributions in statistics and, due to some of its appealing properties, the class that is used in most applications in nance. Here we introduce some of its basic properties. Panel a of Exhibit 3.3 shows the density function of a normal distribution with = 0 and = 1. A normal distribution with these parameter values is called a standard normal distribution. Notice the following EXHIBIT 3.3
Density Function of a Normal Distribution Panel a: Standard Normal Distribution ( = 0, = 1)

32

PROBABILITY AND STATISTICS

pendently normally distributed with = 0.05% and = 1.6%. Then the monthly returns again are normally distributed with parameters = 1.05% and = 7.33% (assuming 21 trading days per month) and the yearly return is normally distributed with parameters = 12.6% and = 25.40% (assuming 252 trading days per year). This means that the S&P 500 monthly return uctuates randomly around 1.05% and the yearly return around 12.6%. The last important property that is often misinterpreted to justify the nearly exclusive use of normal distributions in nancial modeling is the fact that the normal distribution possesses a domain of attraction. A mathematical result called the central limit theorem states thatunder certain technical conditionsthe distribution of a large sum of random variables behaves necessarily like a normal distribution. In the eyes of many, the normal distribution is the unique class of probability distributions having this property. This is wrong and actually it is the class of stable distributions (containing the normal distributions), which is unique in the sense that a large sum of random variables can only converge to a stable distribution. We discuss the stable distribution in Chapter 7.

OTHER POPULAR DISTRIBUTIONS

In the remainder of this chapter, we provide a brief introduction to some popular distributions that are of interest for nancial applications and which might be used later in this book. We start our discussion with the exponential distribution and explain the concept of hazard rate. this leads to the class of Weibull distributions, which can be interpreted as generalized exponential distributions. Together with the subsequently introduced class of Chi square distributions, the Weibull distributions belong to the more general class of Gamma distributions. We continue our exposition with the Beta distribution, which can be of particular interest for credit risk modelling and the t distribution. The log-normal distribution is the classical and most popular distribution when modeling stock price movements. Subsequently, we introduce the logistic and extreme value distribution. The latter has become popular in the eld of operational risk analysis and is contained in the class of generalized extreme value distributions. We conclude the chapter with a short discussion of the generalized Pareto and the skewed normal distribution and the denition of a mixed distribution.5
For a thorough treatment of all mentioned distributions, the reader is referred to the standard reference Johnson, Kotz, and Balakrishnan (1994 and 1995).
5

46

PROBABILITY AND STATISTICS

functions f1,fn and n positive real numbers 1,n with the property i = 1 and dene a new probability density f via f(x) =

i=1

i fi ( x )

The so dened mixed distributions are often used when no well-known distribution family seems appropriate to explain the specic observed phenomenon.

REFERENCES
Embrechts, P., C. Klueppelberg, and T. Mikosch. 1997. Modelling Extremal Events for Insurance and Finance, vol. 33 of Applications of Mathematics. Berlin: SpringerVerlag. Johnson, N. L., S. Kotz, and N. Balakrishnan. 1994. Continuous Univariate Distribution, Volume 1, 2nd ed. New York: John Wiley & Sons. Johnson, N. L., S. Kotz, and N. Balakrishnan. 1995. Continuous Univariate Distribution, Volume 2, 2nd ed. New York: John Wiley & Sons.