Professional Documents
Culture Documents
Presstressed Modal ANalysis
Uploaded by
MardiSantosoCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Presstressed Modal ANalysis
Uploaded by
MardiSantosoCopyright:
Available Formats
Prestressed Modal Analysis Using Finite Element Package ANSYS
R. Bedri and M.O. Al-Nais
College of Technology at Hail, P.O. Box. 1690 Hail, Saudi Arabia Tel: +966 531 7705 ext 240 Fax: +966 531 7704 r bedri@yahoo.com Abstract. It is customary to perform modal analysis on mechanical systems without due regards to their stress state. This approach is of course well accepted in general but can prove inadequate when dealing with cases like spinning blade turbines or stretched strings, to name but these two examples. It is believed that the stress stiening can change the response frequencies of a system which impacts both modal and transient dynamic responses of the system. This is explained by the fact that the stress state would inuence the values of the stiness matrix. Some other examples can be inspired directly from our daily life, i.e., nay guitar player or pianist would explain that tuning of his playing instrument is intimately related to the amount of tension put on its cords. It is also expected that the same bridge would have dierent dynamic responses at night and day in places where daily temperature uctuations are severe. These issues are unfortunately no suciently well addressed in vibration textbooks when not totally ignored. In this contribution, it is intended to investigate the eect of prestress on the vibration behavior of simple structures using nite element package ANSYS. This is achieved by rst performing a structural analysis on a loaded structure then make us of the resulting stress eld to proceed on a modal analysis. Keywords: Pre-stress, Modal analysis, Vibrations, Finite elements, ANSYS.
Scope
In this investigation, we are concerned by the eect of pressure loads on the dynamic response of shell structures. A modal analysis is rst undertaken to ascertain for the eigen-solutions for an unloaded annulus shell using a commercial nite element package ANSYS ([1]). In the second phase, a structural analysis is performed on the shell. Different pressure loads are applied and the resulting stress and strain elds are determined.
Z. Li et al. (Eds.): NAA 2004, LNCS 3401, pp. 171178, 2005. c Springer-Verlag Berlin Heidelberg 2005
172
R. Bedri and M.O. Al-Nais
In the third phase, these elds are then used as pre-stress and new modal analyses are performed on the pre-loaded shell. The details on geometry, boundary conditions, and loading conditions are depicted in the procedure section.
Theory
The equation of motion ([3]) for a body is given in tensorial notation by . + f = 2u t2 (1)
where represents the second order stress tensor, f the body force vector, the density and u the displacement eld. Expressed in indicial notation (1) can be recast as ji,j + fi = i,tt (2)
From the theory of elasticity, we know that the generalized Hookes law relates the nine components of stress to the nine components of strain by the linear relation: ij = cijkl ekl (3) where ekl are the innitesimal strain components, ij are the Cauchy stress components and cijkl are the material parameters. Furthermore, for an isotropic material ([3]) (3) simplies to ij = 2eij + ij ekk (4)
where and are the so called Lame constants. For boundary-value problems of the rst kind, it is convenient and customary to recast (1) in terms of the displacement eld u , amenable to nite element treatment. (5) ( + )grad(divu) + 2 u + f = u These equations are the so called Navier equations of motion ([3]). For the 3-D elasticity problem, this equation becomes an elliptic boundary problem. We can recall that the it is possible to nd a weak form or a Galerkin form ([4]) i.e., L(u, v ) = (f, v ) instead of Lu = f (6) where Lu = f is the generalization of the dierential equation and L is a linear operator and (,) stands for the dot product. The nite element solution: the dierential equation is discretized into a series of nite element equations that form a system of algebraic equations to be solved: [K ]{u} = {F }
Prestressed Modal Analysis Using Finite Element Package ANSYS
173
where [K ] is the stiness matrix, {u} is the nodal displacement vector and {F } is the applied load vector. These equations are solved in ANSYS ([1]) either by the method of Frontal solver or by the method of Conjugate gradient solver. Modal analysis consists in solving an associated eigenvalue problem in the form [k ] 2 [M ] {u} = {0} (7) where [K ] is the stiness matrix and [M ] is the consistent mass matrix that is obtained by [M ] =
v
[N ]T [N ]dv
(8)
[N ] being the shape functions matrix. For the prestressed modal analysis, the stiness matrix [K ] is being corrected to take into account the stress eld.
Procedure
In the preprocessor of ANSYS ([1]) geometric modelling of our eigenvalue problem (modal analysis) and then of our boundary value problem (static analysis) is being dened: an annulus with internal radius r1 = 0.5m and external radius r2 = 0.8m. A corresponding nite element model is obtained by meshing the geometric model using 60 elements. Element type chosen: ANSYS shell 63 see g.(3) in appendix for ample description. Thickness:0.003m Elastic properties: Youngs modulus of elasticity: 193 GPa Poissons ratio:0.29 Material density: 8030 kg/m3 Constraints: mixed type boundary conditions For r = r1 , the six translations and rotations are being set to zero, i.e. u = {0, 0, 0, 0, 0, 0}. 3.1 Modal Analysis: Stress Free Modal Analysis
In the solution processor of ANSYS, modal analysis type is rst chosen with Lanczos ([9]) extraction and expansion method. The eigen solutions obtained are analyzed and presented in the general postprocessor. The rst ve modes of vibration are tabulated in tables 1 and 2. The mode shapes are also included in the appendix. 3.2 Static Analysis
Static type analysis is now selected. Ten dierent sets of pressure loads are being applied to the annulus on its outer boundary i.e., r = r2 . Details can be seen on
174
R. Bedri and M.O. Al-Nais
tables 1 and 2. For each loading case, prestress eect is being activated in the analysis option of the program. The resulting stress eld is then applied when it comes to performing subsequently modal analysis on the annulus. 3.3 Modal Analysis with Prestress Eect
Once the stress eld is being established from the above static analysis, it is applied as prestress to the shell structure through the activation of this option in the subsequent modal analysis. This procedure is reproduced for the twenty dierent preloading cases.
Results
The results of the dierent analyses i.e., modal analysis of the stress free annulus the static analysis and then the modal analysis of the preloaded structure, are all summarized and displayed in tabular form see tables 1 and 2 in the appendix. To ascertain the eect of the prestress level on the modes of vibration, some further calculations are done and presented in tables 3 and 4 in the appendix. Plots of prestress level versus percent increase or decrease in frequencies are plotted respectively in gures 1 and 2.
Comments on Results
5.1. Prestress produces no eect on the mode shapes of vibration of the shell structure. 5.2. By examining the results presented in tables 1 and 2, it is evident that the frequencies are impacted by preloading. The eect of such preloading seems to be more apparent on the rst modes than on the higher ones. The plotted curves of gures 1 and 2 are here to corroborate these conclusions. 5.3. A closer look at these curves discloses that there seems to be a linear correlation between the prestress level and the percent frequency increase or decrease for each mode of vibration. 5.4. Tensile preloading produces an increase in frequency whereas compressive preloading results in a decrease in frequency.
Conclusions
Three pieces of conclusions can be inferred from this study: 6.1. The mode shapes of vibration of the structure are not sensitive to preloading. 6.2. Prestressing seems to impact the dynamic behavior of the structure. 6.3. Tensile prestress acts as a stiener and enhances the dynamic characteristics of the structure resulting in frequency increase. Whereas compressive prestress has a converse eect on the structure by reducing its frequencies.
Prestressed Modal Analysis Using Finite Element Package ANSYS
175
References
1. ANSYS, Users manual, revision 5.6, Swanson Analysis Inc., Nov. 1999. 2. Reddy, J.N.: An introduction to the nite element method , McGraw-Hill, New York 1984. 3. Reddy, J.N., energy and variational methods in applied mechanics, John Wiley, New York 1984. 4. Zienkiewicz, O.C., and Taylor, R.L., The nite element method , 4th ed., McGrawHill, New York, 1989. 5. Bathe, K.J.. Finite element procedures in engineering analysis, Prentice-Hall, Englewood Clis, N.J., 1982. 6. Cheung, Y.K. and Yeo, M. F., a practical introduction to nite element analysis, Pitman, London, 1979. 7. Rao, S.S., The nite element method in engineering, Pergamon Press, Oxford, 1982. 8. Meirovitch, L., Elements of vibration analysis, McGraw-Hill, New York, 1975. 9. Lanczos, C, the variational principles of mechanics, the university of Toronto press, Toronto, 1964. 10. Hutchinson, J.R., Axisymmetric Vibrations of a Solid Elastic Cylinder Encased in a Rigid Container, J. Acoust. Soc. Am., vol. 42, pp. 398-402, 1967. 11. Reddy, J.N., Applied Functional Analysis and Variational Methods in Engineering, McGraw-Hill, New York, 1985. 12. Sandbur, R.B., and Pister, K.S., Variational Principles for Boundary Value and Initial-Boundary Value Problems in Continuum Mechanics, Int. J. Solids Struct., vol. 7, pp. 639-654, 1971. 13. Oden, J.T., and Reddy, J.N., Variational Methods in Theoretical Mechanics, Springer-Verlag, Berlin, 1976. 14. http://caswww.colorado.edu/courses.d/AFEM.d/ 15. http://caswww.colorado.edu/courses.d/IFEM.d/ 16. Liepins, Atis A., Free vibrations of prestressed toroidal membrane, AIAA journal, vol. 3, No. 10, Oct. 1965, pp. 1924-1933. 17. M. Attaba, M.M. Abdel Wahab, Finite element stress and vibration analyses for a space telescope, ANSYS 2002 Conference, Pittsburg, Pennsylvania, USA, April 22-24, 2002. 18. Alexey I Borovkov, Alexander A Michailov, Finite element 3D structural and modal analysis of a three layered nned conical shell, ANSYS 2002 Conference, Pittsburg, Pennsylvania, USA, April 22-24, 2002. 19. Sun Libin, static and modal analysis of a telescope frame in satellite, ANSYS 2002 Conference, Pittsburg, Pennsylvania, USA, April 22-24, 2002. 20. Erke Wang, Thomas Nelson, structural dynamic capabilities of ANSYS, ANSYS 2002 Conference, Pittsburg, Pennsylvania, USA, April 22-24, 2002.
176
R. Bedri and M.O. Al-Nais
Appendix
Table 1. The rst ve modes against the tensile prestress levels Mode 0 1 2 3 4 5 2.602 2.634 2.656 2.790 2.839 Tensile Prestress in N/m 103 2.103 4.103 8.103 16.103 32.103 64.103 Frequency in kHz 2.603 2.604 2.606 2.610 2.618 2.633 2.664 2.635 2.636 2.638 2.642 2.649 2.665 2.695 2.657 2.658 2.660 2.664 2.672 2.688 2.718 2.791 2.792 2.794 2.798 2.805 2.821 2.852 2.840 2.841 2.843 2.847 2.855 2.870 2.901 105 2.105 3.105 2.698 2.729 2.752 2.885 2.935 2.789 2.821 2.844 2.977 3.027 2.876 2.904 2.932 3.065 3.115
Table 2. The rst ve modes against the compressive prestress levels Mode 0 1 2 3 4 5 2.602 2.634 2.656 2.790 2.839 Pressure Prestress in N/m 103 2.103 4.103 8.103 16.103 32.103 64.103 Frequency in kHz 2.601 2.600 2.598 2.594 2.587 2.571 2.539 2.633 2.632 2.630 2.626 2.618 2.602 2.570 2.655 2.654 2.652 2.648 2.641 2.625 2.593 2.789 2.788 2.786 2.782 2.774 2.758 2.726 2.838 2.837 2.835 2.831 2.823 2.807 2.775 105 2.105 3.105 2.502 2.533 2.556 2.690 2.739 2.396 2.428 2.450 2.585 2.634 2.285 2.316 2.338 2.474 2.523
Fig. 1. % Frequency increase versus Prestress
Prestressed Modal Analysis Using Finite Element Package ANSYS Table 3. The percent frequency increase against prestress levels Mode Tensile Prestress in N/m 103 2.103 4.103 8.103 16.103 32.103 64.103 % increase in frequency 0.038 0.077 0.154 0.307 0.615 1.191 2.383 0.038 0.076 0.152 0.304 0.569 1.177 2.316 0.038 0.075 0.151 0.301 0.602 1.205 2.184 0.036 0.072 0.143 0.287 0.538 1.111 2.222 0.035 0.070 0.141 0.282 0.563 1.092 2.184 105 2.105 3.105 3.689 3.607 3.614 3.405 3.381 7.187 7.099 7.078 6.702 6.622 10.530 10.250 10.391 9.857 9.722
177
1 2 3 4 5
Table 4. The percent frequency decrease against prestress levels Mode Pressure Prestress in N/m 103 2.103 4.103 8.103 16.103 32.103 64.103 % decrease in frequency 0.038 0.077 0.154 0.307 0.576 1.191 2.421 0.038 0.076 0.152 0.304 0.607 1.215 2.430 0.038 0.075 0.151 0.301 0.565 1.167 2.372 0.036 0.072 0.143 0.287 0.573 1.147 2.294 0.035 0.070 0.141 0.282 0.563 1.127 2.254 105 2.105 3.105 3.843 3.834 3.765 3.584 3.522 7.917 7.821 7.756 7.348 7.221 12.183 12.073 11.973 11.326 11.131
1 2 3 4 5
Fig. 2. % Frequency Decrease versus Pressure Level
178
R. Bedri and M.O. Al-Nais
Fig. 3
Fig. 4
You might also like
- Fem NotepadDocument5 pagesFem NotepadVivek KhareNo ratings yet
- 1 s2.0 0045794987900265 MainDocument13 pages1 s2.0 0045794987900265 Maincutemrinal5No ratings yet
- Belytschko Time IntegrationDocument29 pagesBelytschko Time IntegrationFoopiewNo ratings yet
- Materials & Properties: Mechanical Behaviour: C. GarionDocument19 pagesMaterials & Properties: Mechanical Behaviour: C. GarionJosePeterPintoNo ratings yet
- Closed-Form SolutionsDocument13 pagesClosed-Form SolutionsBza ZaBugNo ratings yet
- Modeling of Large Deformations of Hyperelastic MaterialsDocument4 pagesModeling of Large Deformations of Hyperelastic MaterialsSEP-PublisherNo ratings yet
- Analysis of Truss-Cable StructuresDocument9 pagesAnalysis of Truss-Cable StructuresKtk ZadNo ratings yet
- An Updated Reference Configuration FormuDocument12 pagesAn Updated Reference Configuration FormuMiroslav ZivkovicNo ratings yet
- Finite Element Analysis and Reliability Assessment of Spherical LPG ...Document6 pagesFinite Element Analysis and Reliability Assessment of Spherical LPG ...Suleyman HaliciogluNo ratings yet
- Gord Is 1979Document12 pagesGord Is 1979NixonNo ratings yet
- Experimental Force Identification by Using Natural OptimizationDocument9 pagesExperimental Force Identification by Using Natural OptimizationbrucemlsNo ratings yet
- Finite Element Analysis Interview QuestionsDocument7 pagesFinite Element Analysis Interview QuestionsRajesh Perumal100% (7)
- (2002) A Finite-Element Model For The Analysis of Wrinkled Membrane StructuresDocument21 pages(2002) A Finite-Element Model For The Analysis of Wrinkled Membrane StructuresGregorius FilipusNo ratings yet
- (Hinton, 1976) A Note On Mass Lumping and Related Processes in The Finite Element MethodDocument5 pages(Hinton, 1976) A Note On Mass Lumping and Related Processes in The Finite Element MethodLeon Valencia RestrepoNo ratings yet
- Radial Return Method Applied in Thick-Walled Cylinder AnalysisDocument15 pagesRadial Return Method Applied in Thick-Walled Cylinder AnalysisAndré RodriguesNo ratings yet
- Mindlin Eshel 1968Document16 pagesMindlin Eshel 1968Don't BeCuriousNo ratings yet
- Sheet - Ansys, SpringbackDocument9 pagesSheet - Ansys, Springbacksupersonny007No ratings yet
- Numerical Fracture MechanicsDocument4 pagesNumerical Fracture Mechanicsg401992No ratings yet
- Isotropic Linear Elastic Stress ConcentrationDocument19 pagesIsotropic Linear Elastic Stress ConcentrationIoan-Lucian StanNo ratings yet
- Nlaa8 - 537-549 - Co The Tham Khao DuocDocument14 pagesNlaa8 - 537-549 - Co The Tham Khao Duocpuka2427No ratings yet
- 0263 8231 (84) 90004 1 PDFDocument22 pages0263 8231 (84) 90004 1 PDFjuan carlos molano toroNo ratings yet
- cobaCES53 56 2018 2Document10 pagescobaCES53 56 2018 2miltoncobaNo ratings yet
- Simo1985 (Consistent Tangent)Document18 pagesSimo1985 (Consistent Tangent)Athila Vieira Lima UFCNo ratings yet
- 3-Problems in ElasticityDocument58 pages3-Problems in Elasticityali381100% (1)
- Ondas DinâmicasDocument16 pagesOndas DinâmicasivyjeannNo ratings yet
- Finite Element Implementation of Incompressible, Transversely Isotropic HyperelasticityDocument22 pagesFinite Element Implementation of Incompressible, Transversely Isotropic HyperelasticityManuelNo ratings yet
- Dynamic Stress Analysis of A Bus Systems: H. S. Kim, Y. S. Hwang, H. S. YoonDocument10 pagesDynamic Stress Analysis of A Bus Systems: H. S. Kim, Y. S. Hwang, H. S. YoonrajagudipatiNo ratings yet
- (Hallquist) A Simple Rigid Body Algorithm For Structural Dynamics ProgramsDocument27 pages(Hallquist) A Simple Rigid Body Algorithm For Structural Dynamics ProgramsMariano SerranoNo ratings yet
- Umat DocumentationDocument47 pagesUmat DocumentationNgoc-Trung NguyenNo ratings yet
- Otter 1966Document24 pagesOtter 1966Pedro SilvaNo ratings yet
- Viscoelastic ModellingDocument18 pagesViscoelastic ModellingNimisha VedantiNo ratings yet
- Theory of Elastisity, Stability and Dynamics of Structures Common ProblemsFrom EverandTheory of Elastisity, Stability and Dynamics of Structures Common ProblemsNo ratings yet
- Module 1Document45 pagesModule 1MD SHAHRIARMAHMUDNo ratings yet
- Drilling DOFDocument11 pagesDrilling DOFDaniele Di LucaNo ratings yet
- Bem Project Must UseDocument22 pagesBem Project Must UseFemi Richard FakoyaNo ratings yet
- Notes For FemDocument35 pagesNotes For FemG. Somasekhar SomuNo ratings yet
- Introduction To Finite Elements (Matrix Methods)Document46 pagesIntroduction To Finite Elements (Matrix Methods)Paulo FidelisNo ratings yet
- Periodic - Boundary - Condition - Technique - On - Carbon - FiDocument9 pagesPeriodic - Boundary - Condition - Technique - On - Carbon - FiNew SainNo ratings yet
- Aim:-Study of FEM (Finite Element Method) Finite-Element MethodDocument9 pagesAim:-Study of FEM (Finite Element Method) Finite-Element MethodAshley Silvester AnthonyNo ratings yet
- Lyapunov Stability Analysis of A Mass-Spring System Subject To FrictionDocument27 pagesLyapunov Stability Analysis of A Mass-Spring System Subject To FrictionGrecia GarciaNo ratings yet
- A Particle Method For History-Dependent MaterialsDocument18 pagesA Particle Method For History-Dependent Materials1368960034No ratings yet
- FINITE ELEMENT ANALYSIS - Unit Wise - Question Bank (Part A & B) & Unitwise - Important FormulaeDocument49 pagesFINITE ELEMENT ANALYSIS - Unit Wise - Question Bank (Part A & B) & Unitwise - Important FormulaeS A ABDUL SUKKUR83% (12)
- Cheng Wang PaperDocument13 pagesCheng Wang PaperRahul7LMNo ratings yet
- Introduction To Finite Element AnalysisDocument20 pagesIntroduction To Finite Element AnalysisVishnu Vardhan Reddy GangapuramNo ratings yet
- Application of Theorem of Minimum Potential Energy To A Complex Structure Part II: Three-Dimensional AnalysisDocument29 pagesApplication of Theorem of Minimum Potential Energy To A Complex Structure Part II: Three-Dimensional AnalysisbenyfirstNo ratings yet
- Finite Element by Tarun KantDocument7 pagesFinite Element by Tarun KantVijayraj11No ratings yet
- Transversely Isotropic Plasticity With Application To Fiber - Reinforced PlasticsDocument20 pagesTransversely Isotropic Plasticity With Application To Fiber - Reinforced Plasticsshossain1987No ratings yet
- On The Computation of Plastic Stress-Strain Relations For Polycrystalline MetalsDocument9 pagesOn The Computation of Plastic Stress-Strain Relations For Polycrystalline MetalsChandra ClarkNo ratings yet
- Evaluation of Engineering Stresses As The "Correct" Measure of "Physical" Stresses in Large Strain Geometrically Nonlinear ProblemsDocument12 pagesEvaluation of Engineering Stresses As The "Correct" Measure of "Physical" Stresses in Large Strain Geometrically Nonlinear ProblemsBreno NogueiraNo ratings yet
- 2order D CorrectedDocument32 pages2order D CorrectedslirpaNo ratings yet
- Johannsen 2002Document8 pagesJohannsen 2002ALEJANDRO GANCEDO TORALNo ratings yet
- Energy Principles and Finite Element Methods For PDocument15 pagesEnergy Principles and Finite Element Methods For Paarvee.armoorNo ratings yet
- Obtaining Stresses and Strains From Ods Data:) T (X&) T (X&Document7 pagesObtaining Stresses and Strains From Ods Data:) T (X&) T (X&ho-faNo ratings yet
- A Mixed-Enhanced Formulation For Tetrahedral Finite ElementsDocument24 pagesA Mixed-Enhanced Formulation For Tetrahedral Finite ElementsAlfito Januar HNo ratings yet
- Stabilization of Euler-Bernoulli Plate Equation With Variable Coefficients by Nonlinear Boundary FeedbackDocument21 pagesStabilization of Euler-Bernoulli Plate Equation With Variable Coefficients by Nonlinear Boundary FeedbackAndrew ThomasNo ratings yet
- 1998 Investigationo F Stressesa T The Fixed End of Deep Cantilever BeamDocument10 pages1998 Investigationo F Stressesa T The Fixed End of Deep Cantilever BeamFABIANCHO2210No ratings yet
- Colloidal SystemDocument13 pagesColloidal SystemCristinaNo ratings yet
- Wagner, Holian, Massively Parallel Molecular Dynamics Simulations of Two-Dimensional Materials at High Strain RatesDocument6 pagesWagner, Holian, Massively Parallel Molecular Dynamics Simulations of Two-Dimensional Materials at High Strain RatesBishwajyoti DuttaMajumdarNo ratings yet
- CORE WALL Analysis - Moment Frame & Shear Wall Engineering - Eng-TipsDocument8 pagesCORE WALL Analysis - Moment Frame & Shear Wall Engineering - Eng-Tipsgreat2008100% (1)
- The Open Construction & Building Technology JournalDocument16 pagesThe Open Construction & Building Technology Journalgreat2008No ratings yet
- Petia Tzokova: Methodology Case StudiesDocument1 pagePetia Tzokova: Methodology Case Studiesgreat2008No ratings yet
- Pre Panelized Load Bearing Metallic Studs: Presented by Uma MullapudiDocument12 pagesPre Panelized Load Bearing Metallic Studs: Presented by Uma Mullapudigreat2008No ratings yet
- Femap TutorialsDocument16 pagesFemap Tutorialsgreat2008No ratings yet
- Ansys Tips and Ansys TricksDocument54 pagesAnsys Tips and Ansys Trickssrinath_iitmNo ratings yet
- Strain-Rate Sensitive Behavior of Cement Paste and Mortar in CompressionDocument9 pagesStrain-Rate Sensitive Behavior of Cement Paste and Mortar in CompressionAnonymous gq7UQAwNo ratings yet
- 4/4/2014 Hareesha N G, Asst Prof, DSCE, Blore 1Document21 pages4/4/2014 Hareesha N G, Asst Prof, DSCE, Blore 1Kiran KumarNo ratings yet
- 14.7.6 Steel-Reinforced Elastomeric Bearings - Method A: AASHTO LRFD Bridge Design Specifications, 8th Edition (2017)Document8 pages14.7.6 Steel-Reinforced Elastomeric Bearings - Method A: AASHTO LRFD Bridge Design Specifications, 8th Edition (2017)jrjdengineersNo ratings yet
- Thermal Analysis of FRP Chimneys Using Consistent Laminated Shell ElementDocument20 pagesThermal Analysis of FRP Chimneys Using Consistent Laminated Shell ElementpetronashscribdidNo ratings yet
- Experimental Stress Analysis Two Marks With AnswersDocument24 pagesExperimental Stress Analysis Two Marks With Answersmatrixrajiv34100% (2)
- Tensile Test Lab ReportDocument4 pagesTensile Test Lab ReportElisha NissiNo ratings yet
- 2D Numerical Simulations of Soil Nail WallsDocument12 pages2D Numerical Simulations of Soil Nail WallsShahab KhaledNo ratings yet
- Temperature Effects On Laminated Glass at High RatDocument10 pagesTemperature Effects On Laminated Glass at High RatAniket InarkarNo ratings yet
- S BeamDocument12 pagesS Beamwisnu_bayusaktiNo ratings yet
- Pressure Vessel DesignDocument68 pagesPressure Vessel DesignAchuat Deo0% (1)
- Modulos Resilient 031214Document15 pagesModulos Resilient 031214faisalNo ratings yet
- CH 6 Differential Analysis of Fluid FlowDocument30 pagesCH 6 Differential Analysis of Fluid FlowMubashir GulzarNo ratings yet
- Utilization of Upgraded Shredder Blade and Recycling The Waste Plastic and Rubber TyreDocument6 pagesUtilization of Upgraded Shredder Blade and Recycling The Waste Plastic and Rubber TyrePhilip ArpiaNo ratings yet
- Reinforced Concrete Structures II - Chapter 1 PDFDocument51 pagesReinforced Concrete Structures II - Chapter 1 PDFabenezer abrhamNo ratings yet
- Analyses of Bolted Joint For Bolt Preload and Shear LoadDocument17 pagesAnalyses of Bolted Joint For Bolt Preload and Shear LoadAndy YanNo ratings yet
- Handbook To SSC JE Mechanical-1Document223 pagesHandbook To SSC JE Mechanical-1abhimanyu100% (4)
- Andrzej LitewkaDocument21 pagesAndrzej LitewkaVicente Bergamini PugliaNo ratings yet
- Andjelkovic 2015 - Modelling of Shear Characteristics at The Concrete-Rock Mass InterfaceDocument15 pagesAndjelkovic 2015 - Modelling of Shear Characteristics at The Concrete-Rock Mass InterfaceTiago BorgesNo ratings yet
- 2019 DSSIMULIA - Established - Damaged Plasticity Model For Concrete and Other Quasi-Brittle MaterialsDocument11 pages2019 DSSIMULIA - Established - Damaged Plasticity Model For Concrete and Other Quasi-Brittle MaterialsPhan Đào Hoàng HiệpNo ratings yet
- 1993 - Investigation of Footing Restraint On Stability of Large Scale Reinforced Soil Wall Tests PDFDocument10 pages1993 - Investigation of Footing Restraint On Stability of Large Scale Reinforced Soil Wall Tests PDFTomaz TurcarelliNo ratings yet
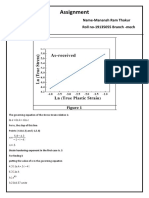
- Assignment: Name-Manansh Ram Thakur Roll No-19135055 Branch - MechDocument3 pagesAssignment: Name-Manansh Ram Thakur Roll No-19135055 Branch - MechManansh ThakurNo ratings yet
- Strength Lab No. 6-Creep TestDocument9 pagesStrength Lab No. 6-Creep Testjohn rozz bbNo ratings yet
- Strain Gage-WhatDocument16 pagesStrain Gage-WhatAshok JoshiNo ratings yet
- Punching Shear Strength and Deformation For FRP-reinforced Concrete Slabs Without Shear ReinforcementsDocument22 pagesPunching Shear Strength and Deformation For FRP-reinforced Concrete Slabs Without Shear ReinforcementsPratik MuthaNo ratings yet
- Fracture Mechanic ACIDocument71 pagesFracture Mechanic ACIHarun AlrasyidNo ratings yet
- Bridge Bearing2Document10 pagesBridge Bearing2sandbad2No ratings yet
- Investigation of Stresses in Ring Stiffened Circular CylinderDocument5 pagesInvestigation of Stresses in Ring Stiffened Circular Cylinderisraaahmed12No ratings yet
- Review Module - Working Stress DesignDocument1 pageReview Module - Working Stress DesignDream CatcherNo ratings yet
- Design of Axially Loaded Compression MembersDocument13 pagesDesign of Axially Loaded Compression Membersmayka mawrinNo ratings yet