Formal/ Informal Reasoning

The graph of a quadratic equation is represented by the equation:

. This equation
represents a parabola:




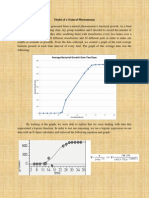
Informal Reasoning: By looking at the graph, we can identify the roots (where the function passes the x-
axis) by simply using the visual representation. Since this graph passes the x-axis, the roots can be easily
identified. However, when we have a graph that doesnt touch the x-axis, like the following, we use the
Quadratic Formula to help us find the complex roots.






Formal Reasoning: The Quadratic Formula is used to find real and complex roots of a graph. Its equation
is the following:

This equation can be derived from the original Quadratic Formula and the steps are the following:






Step 1.

Step 2.

-c -c

Step 3.

Step 4.

= (

Step 5.

Step 6.

Step 2. In this step, we subtract c from both sides so the two
variables with an x will be on one side and the constant c
on the other.


Step 3. Next, we divide both sides by a so we can get the

by itself. This will make factoring/ completing the square
easier.



Step 4. In this step, we are completing the square in order to
factor the expression on the left.









Step 5. We are multiplying

by

so that it can have the

same denominator as

. This will make it a lot easier

to subtract the two fractions since they will have a
common denominator.


Step 6. We then take the square root on both sides in
order to get x by itself.

Step 7:

Step 8. :

Step 9.

Since the Quadratic Formula is used to find the roots of a graph, it can be applied informally (by simply
looking at the graph and seeing where the function crosses the x-axis), and formally by deriving and
using the Quadratic Formula.