Physics Factsheet @ 2 AEM wee) Dire ae Capacitors Introduction ‘Capacitors are widely used in electrical engineering and electronics. They are important in any physics course because ofthe Variety of uses they have, A very simple capacitor consists of two parallel metal plates a Vo ‘The capacitor is frst connected to a dc. supply and then to a sensitive ammeter (or galvanometer) When the capacitor is connected tothe sensitive ammeter, a momentary deflection is observed. This deflection isa brief pulse of charge and illustrates an important idea with capacitors, ‘We say “a capacitor stores charge”. We use the symbol @ to represent ‘the amount of charge involved. In this case, charge Qi taken from the dc supply, stored on the capacitor plates and then the same charge Q discharged, through the ammeter. ‘Remember tha the unit of charge isthe coulomb (abbreviation Ch. Although one coulomb i a small amount in current electricity, isan ‘enormous amount in static electricity. In capacitors, the charge stored is static and we use much smaller units, pically mirocoulombs UC. Although a capacitor can be made from any two conductors close to each other, we have considered the simplest case where the ‘conductors are two parallel metal plates. You should also note that the plates are separated by an insulator, inthis case ait. The insulating material iscalled the dielectric, Because the dielectric isan insulator its clear that steady dc. current cannot pass through a capacitor and this is why we ‘only get the bref pulse of charge referred to above. Te symbol ee acacia —| she shone aga ceed wi iy 12), 1 Notice thatthe plates are marked + and ~ and that these signs correspond to those on the de, supply. You might think thatthe charge stored is 20. This is norso, Ask yourself ‘how much charge is flowing through the ammeter during discharge. Only the amount @ flows from the postive plate, through the ammeter, and ‘neutralise’ the charge on the negative plate, ‘Toinvestgate the charge stored on capacitor we can use ‘coulomibmeter’ ‘When a coulombmeter is connected ta charged capacitor. it will take all the charge from the capacitor, measure it and display the result on a digital readout. jy right roche swite \ Sf) coulomb © = iter By depressing the left hand key of the rocker switch, the capacitor is charged to a potential difference V which can be adjusted by the variable d.c-supply. Upon depressing the right hand key, the stored charge Q is ‘measured and displayed by the coulombmeter. ‘Table 1 shows the charge stored for various potential ferences upto 10 vols, Tabled ry Tein 7]° ]s charge we | + [8 m [16 | 20 ‘The results are displayed in the graph below. You can see that there is a linear relationship, charged 20 T Ta The ratio 2 isthe gradient ofthe sagt ie so 2 constant PH This constant is called the capacitance ofthe capacitor. Charge stored potential difference ‘The unit of capacitance is the farad (F). To calculate the capacitance ‘@ must bein coulombs and Vin volts. Because the coulomb is a large unit so also is the fara, In practice you will use submultiples as shown in table 2 Table2 factor prefix name symbol Fel milifarad mF Fai mnlcrofarad iF Fao nanofarad nF Five picofarad ?F —_———_—@£@-| — 9 ——\—!@Capacitors Physics Factsheet ‘To calculate the capacitance ofthe capacitor inthe graph, we can use the last point (20 uc. 10v) 2 c= c= x10 i) 2x 108 F 2 uF (2 microfarads) ‘Any pair of readings in table 1 could have been used giving the same answer, ty using one or two yourself. In each case you are finding the gradient ofthe line on the charge against potential difference graph, If you do a real experiment, your readings will probably not increase ‘uniformly as in table 1 In this ease you plot all the points and then deaw the best straight line passing through the origin. The gradiens ofthis line ives the average value forthe capacitance. Exam Hint: If you are working out the gradient of a line, or doing ‘any calculation, always look carefully at the units to see if metric prefixes are being used. Capacitance ‘The size and separation of the plates affects the capacitance. ‘The two quantities you need ate area of overlap of the plates A and the plate separation d. area of overlap A Experiments show that: + capacitance varies directly with the area A, Coe A. Combining tise wo ives: ‘To change from a proportionality to equality we introduce a constant of proportionality inthis case We can now wrt the equation Ce, We se the subscript 0 when there ming betncen the pats (Sl there should bea vactum between he pes but he pres at makes snes no difeence) ‘The term g, epsilon nought, is called “the permitivity of free space; its value is given by (e, = 8.85 x 10-* For" (farads per metre) ‘The units for e, canbe Found by rearranging the equation above and then putting in the known units units for So far we have been thinking that the space between the plates is air ora vacuum, What will happen if an insulator, she dielectric is inteoduced ‘between the plates ? The answer is thatthe capacitance will be increased bby several times. The factor by which itis increased is between 2 and 10 for most dielectrics and is called the relative permittivity e,. Note that does not have any units, it simply ‘multiplies up" the capacitance (see table 3). Table3 Material Relative permittivity & Air 1.00053 Paper 35 Mica aa Wax paper a GH Epressionjoreapactance C = 24,4. where A= common area ofthe plates (n*) oe d= separation between the plates (m) @, = relative permittivity (no units) @, = constantofproportonality (8.85.10) (ene!) Worked example capacitor is made from two paralle! metal plates with a common area of Im® and a separation of Imm (¢, = 8.85 10-" Fn-') (a) calculate the capacitance where A= In?and d =10°%m. ihre 8 ASHI B $0, €= 885% 10" (b) Ifthe plates are now held apart bya thin sheet of paper 0.1 mm thick, calculate the new capacitance, (Relative permitvity for paper = 3.5) eA. sy cx dSX885 102 HET Ce = 31 xI0°F ee 4 a The area A must be inn? 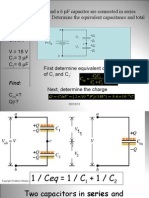(normaly smal) and separation must be im Remember: In the expression for capacttance,C Combining capacitors in parallel and s ‘The following are not proofs but aim to help understanding. ‘The diagram below shows two capacitors C, and C. in parallel, You can see that the area of C, is added to that of C, So, you can see that the total capacitance C,= C,+C, c +0, H ——* +0, Another way to look at capacitors in parallel is to look at their charge. In this case the total charge is found by adding 0, and 0,, = —————————Capacitors Physics Factsheet ‘The diagram below shows two capacitors C, and C, in series. The — Energy stored in a capacitor. values of the capacitors may be different but the charge on each isthe same. As well as storing charge, a capacitor must store energy. You can see this is true because work has to be done to charge the capacitor and energy is 70-2 40-0 released during discharge. For a capacitor, the energy stored is the area — under the graph of voltage against charge. t 7 pad You can see this by ooking a the two inner plates, one from each capacitor L and remembering that they are insulated from the rest of the eiruit. The ‘ charge lost by one plate must equal that gained by the other. The total charge stored here is 0. Look at diagram below showing the equivalent capacitor with an increased is reduced. cation and base C= he tt apctane¢ Charge Itis found using the formula 72 Here, this isa triangle. sow =4 9, x v, Ifyou use are found: and substitute for and then V two oer expesons ‘or capacitors in series GH Frersy stored na capacitor = OV [Worked example [wo capacitors of Sp and 2aP are connected in parallel anda dc. Jupply of 0 volts applied to the combination, Calculate: [id the charge on each, the total charge stored, ‘Typical Exam Question | iii) the total capacitance of the combination, A 10pP capacitor, lv) the charge stored on the combinati supply. Calculate (i) the charge transferred from the supply tothe capacitor (id) the energy taken from the supply (iy the energy stored inthe capacitor. ted toa 2 volt ally uncharged, is com Answer: From the definition for capacitance 0,= 5% 10°50 Answer: () Fromthe definition of capacitance = CXV. So, O = 10"x2 = 20 pC (i) The supply provides 20UC ata steady pd. of 2 volts The energy taken from the supply, W 1s given by W= 40V. So, W= 200% 2 = 4OpF Remember: for capacitors in parallel, the potential diference across WY iy Any ofthe three expressions can be used to find the energy in cece the capacitor: suppose we use W = '4QV This gives Wax 20% 2 = 20) Ji) Again ise = CX V with C= TUF 7x SOC = 350C Note that the answers to ii) and i) are the same. 50) Typical Exam Question [Two capacitors of 16uF and 48uP are on connected in series and a | Note that because we te using W-=Y40V the energy isin joules when the d.c. supply of 40 volts applied to the eombinati charge isin coulombs and the pin volts. With capacitors, itis quite Calculate 16 ue 38 uP commonto ave microjoutes. fi) the total capacitance sro +0 i) the total charge stored 1 ‘Wha charge Q colons moves tioagha posnial diferencs of vos it) the charge on each capacitor <—s0V—> | Jie work done is ov Only al of ths stored inthe capacitor! What as iv) the potential diference across each capactor happened tothe ther hl? tis had to belive but the answer tha the Aer sighs hosts eatin the conecting leas ncharging te cpacor iy vag wetoe La feds thre icant fore satineTiscuet pases tough eseance ‘ofthe leads and gives the joule heating effect (xR), Note thatthe resistance (i) ins © we have sored charse Q = 124 ‘ofthe leads i usually very small and consequently is ignored in most Gti) The charge om each capacitor (in series) mast be the same Hence Qj. = 480 jC and Og = 480 pC 9) Rearange C= & sav, 28 48010 _ soy, 2 V6 = Tae Saar = 10V (Note that 30V + 10 ‘Remember: for capacitors in series, the charge on each capacitor must be the same and the applied potential is divided 800Capacitors Physics Factsheet ‘Time constant Inthe diagram the capacitor is first charged from the 6 Vsupply and then discharged through the 442 resistor &. The question is ‘how will the charge leak away from the eapactor through the resistor R=4KO ial charge is found by using. as shown on the graph charge /wC 2 0 time /ms ‘All other values are found from the equation g = 9, xe In this equation, ¢ means exponential, and may be found on a calculator. Look for the button marked e* and check for yourself that e'= 2.718. and e* = 0.37 (to 2s.) (see Factsheet 10 Exponentials and Logarithms) The equation and graph describe an exponential decay. All {you need to do is to let r= RC in the equation. You will then have: O=0, xe" Q=0,x037 ‘The term RCis called the time constant, itis the ime taken forthe charge stored to fall 10 0.37 or to 37% of the original charge. ‘The time constant for the circuit is 1=RC t= 4x 10° 2x 10° seconds 18> 10%5 (8 ms) ‘The graph above it shows the initial charge Q, = 12s caleulated above, ‘The time constant is Sms, so the charge remaining at tha time should be Wwe x 037 =4.44uc. Not only does the charge fall exponentially but the current and pd decrease ‘exponentially as shown inthe two graphs below and they have the same time constant of 8 mes: current /mA, 18 0 10 time/s ‘After te time constant, r= RCO. V, and Lal fll to 0.37 oftheir original vale, ‘Sometimes we may need to know when these quantities fall 10a half of their original value. This time is obviously slightly less than RC and is approximately 0.7 x RC seconds. (The exact value is found by using the natural logarithm of 2, n2 = 0.6931. You will meet In in calculations on halflife in radioactivity), ‘The tine for, Vand ofall ar ogi vals issvenby: 7 = geiad T,,= RC x0.69 approximately ——$_$_Capacitors Physics Factsheet Exam Workshop In this question, take the permitivty of free space e, = 8.85 x10-" Fn A student has to design a parallel plate capacitor of value 13 pF. (a) Estimate the common area of this capacitor if the dielectric ‘used is air of uniform thickness 0.1 mm, a at alot Ati Ag y= St = BN 8 ga rarxio'm? 28 a & asx This candidate has quoted the correct Tormula and substituted the given values but failed to write Cin Farads (13 10°). The high value produced should have given a hint that something was weong. o ‘an improved design, the student fills the space between the plates with an insulator which is only 0.01 mm thick with a ty ¢, = 5. Estimate the new common area. 2) af ww ecl¥ tog nn 17x10 tw 9 Haas conrectly recognised and used relative permittivity. Fora given capacitor reducing d will educe A in same ratio, Note the candidate thas been awarded full credit for using the wrong answer from 1) (¢) A capacitor is conected in parallel with a high resistance voltmeter V in a circuit with @ 10 volt supply and switeh S. t uF Upon closing the switch, calculate; the pd across the capacitor and the charge stored in it. Q Pdacross capacitor = supply pd = 10V 7 Q= CV Q=13 X10" 10=130 micro-coulombs 7 2 [Has now correctly worked in micro-coulombs. (@) When the switch has been open for 4 seconds, the voltmeter reads 6 volts. Calculate: (the charge rem: i in the capacitor. a cata 4s °V, 50 0, rene m the time constant for the capacitor voltmeter combination. i) 05I=RC® 24 = Qe ‘Candidate has calculated Ing Dat then equated to RC. ‘Common sense should have told him/her thatanegative answer was, ‘wrong. Svhe as also ignored the Exai 13x 10° 0.1 107 ¥ ASK 10 Wed 13% 10° 01x 10° BaSx 1071S = 9.79 mo 310% 10 =130 uc (2) 0) asin answer wey wm o=o, a ingrars0” =78s¥ Typical Exam Question a} Two capacitors are available, one of 2a and one of SF. Each ‘capacitor is given a charge of 300uC. Calculate the potential difference across each. 1) The 2F capacitor is now in the ciruit shown below. A) mitiammeter Que Caleulate: (the charge which flows through the mill oscillates with a frequency of 200 H: ) the frequency at which the switeh should vibrate in order to producea current of mA. Charge stored 2 oc=$v 4) Bydefinition, capacitanc Dotential difference For uk, = 150 Volt % for SHE: 60 Volt ¥ b) (i) Fromdefintion, = VC, so charge stored Q = 10% 2 = 20UC or 20x 10°C ¥ (1) We(should know that currents the charge eivcating in 1 Second. Since the switch oscillates 200 thnes in ne second the charge circulating inthis tne ts (20% 10°) % 2006. % This is 4000 x 10 coulombs in 1 secbnd = 4% 10" coulombs {nL second =Amilicoulombsn 1 second. Hence, current=4mA ¥ (i) required current = 10 mA which is 10% 10" coulombs in 1 second, 7 Working in microcoulombs, this becomes (10 x 10°) x 10 tmicrocoulombs in 1 second, = 10{\C in 1 second. Charge is still being “delivered” in pulses of 20 UC ¥ so the umber of pulses per second or frequency wil be 10 OnY Se = 500 ——— ?——Capacitors Physics Factsheet Questions 1. Inthe circuit shown below, the capacitor is initially uncharged and then the switchs is closed. 5Ma (a) Find the initial current, charging the eapaitor (b) Find the current charging the capacitor when the charge stored on the capacitor is i) Oc i) 190 xe () Find the maximum charge stored by the capacitor. (@) Sketch a graph to show how the charge stored on the capacitor varies with the time from when the switch is closed {e) What isthe gradient at the origin on the graph you have drawn? 2. nthe diagrams al the resistors ate of equal value and all the capacitors are of equal value. The circuit in Fig 1 has a time constant of T. What are the time constants for Fig 2 and Fig 3 = SH ei 3. The circuit below has a 12 volt supply and two capacitors C, and C, Theswith Ss contested tema i] [oes Teene ‘Typical Exam Question ‘The diagram below represents a thunder cloud 5.0m 5.0 kam and 1.0km above the ground. Skin (a) Estimate the capacitance of the cloud-earth system stating any assumptions you make. (b) Ifthe maximum potential difference between the cloud and earth is 1.0 GV calculate the maximum charge stored and the corresponding energy. (€, = 8.85 x 10-" Far) Answer (a) Assumptions are ‘+ to treat the cloud - earth system as a parallel plate capacitor with dimensions given. + airasdielectric so that €, is approximately 1. The capacitance is found from C Points 10 watch are the units 0 area A=(S x 101) x(5% 10! 5% 10° and d= 10° m 5 10 885 910° © 76 21 10° F on, 22 x IF 10 2s Incalculating charge, remember that 1GV = 10° V. In this case,using = CV, = 2.2% 10" 10" = 2.2 x 10° coulomb (b) Tocalculate the energy, any ofthe three expressions may be used. Using W = KOV we have W = 142.2% 10° 10° = 11x10" J. Note that in questions ofthis type, we are only estimating our final value Hence ir seems sensible to give answers 19 no more than 2 significant |/isures. Asa rule, be guided by the figures supplied. n the above, £18 siven to 3 sg fig. but the rest only to 2 sig, fig. So the answer must be 10 2sis. fi. Youmay wonder what the difference is between lengths of Sk, 5.0m, and 5.00km. The answer is that the calculation will show no difference but the information supplied is telling you the number of significant figures to which you should work (a) Calculate the charge stored on C, (b) The switch $ is then connected directly to terminal Calculate: (@) the capacitance of the capacitor combination (Gi) the potential difference across the capacitors and, (ii) the charge on C, (©) The circuits now modified by replacing C, with resistor R= 16MQ, ‘The switch is again moved dieclly from ato, 16 Ma. Calculate the charge on C, 60 seconds after closing 8 Answers 1 (a)20pA () 16 HA (o) pA (@) see paged (e) gradient = initial current 2. all three have the same time co 3. (a) 60 ue (b) (@) OF ti) 10v {i)50 we (© 0= 0, %0%=60%0472=28ue