CHAPTER 3 Limits 3.1 From Secants to Tangents Practise Section 3.1 Page 127 Question 1 a) 4) mgy = 4.75 i) may = 3.8125 iv) mpg = 3.015 025 ¥) mpg = 3.001 500 25 vi) mpg = 1.75 Vii) myo = 2.3125 Vili) mpg = 2.8525 3.1 From Secants fo Tangents MHR 99ix) mp = 2.985 025 X) ming = 2.998 500 25 1) Thefirt five xvalues approach 2 from above. The Jas five x-values approach 2 from below €) The slope of the tangent othe curve at 2.2) ap- pears tobe 3 a yoy =m) y-2=30e-2) ys3x-4 ‘The equation of the tangent is y = 3x 4. Apply, Solve, Communicate Section 3.1 Page 128 Question 3 4) The slope of the graph of V versus represents the rate in L/min, at which the water is draining from the tank, » Estimates may vary. Draw an approximation to the tangent at P(20, 1080) and calculate its slope. ay ok 1450 ~ 725 Draw an approximation to the tangent at R(3S,270) and calculate its slope. 5 10 15 20 25 30 36 40! 100 MHR Chapter 39 ve 3500 4 3000 4 2500 | 2000 + 1500 | 1000 500 + R } 5 10 15 20 25 30 35 do! a vA 3500 | 3000 4 2500 4 200] 100 4 . 1000 4 soo | Qe. {____~>" 5 fo 15 20 25 30 35 40! ‘The Tangent operation yields a slope of ~72 at P as ‘compared to values of ~72.5 and ~72 from b) and c). Determine the slopes of secants NP and PR. 2430 — 1080 3-30 ‘The slope of the tangent at P is approximated by aver- aging the slopes of the secants NP and PR. =90 + (54) =-2 Determine the slopes of secants QR and RS. 480-270 mon = Oa =-42 270 - 120 mes = 3540 =-30 ‘The slope of the tangent at R is approximated by aver- aging the slopes of the secants QR and RS. _ 82+ (230) ‘Quadratic regression yields the following equation = 1L.2F — 1201+ 3000 ‘The Tangent operation yields a slope of ~36 at R as ‘compared to values of ~33 and ~36 from b) and d) 3.1 From Secants to Tangents MHR 1011) The Tangent operation gives a slope of -96 at r = 10, ‘Thus, water is lowing from the (ank ata rate of 96 L/min, Section 3.1 Page 128 Question 4 a) DAL fi) Atr=4, iit) At ©) No. No. 4) Answers will vary 102 MHR Chapter 3 mag + Ma fii) my = Moet eD 2 z 3007 225 375-300 525-450 | 450-3 3 34 is o-5 15415 2Section 3.1 Page 128 Question 5 a) From the intercepts, the slope of the tangent at Mb) Two points on the function are L(2, 5) and N(S, 1.25), 402 can be estimated 4 canbe estimated as ~ 4, or 10 3 of the slopes of the two secants ig ~~ C975) g, 0.625, ©) The results from the table below suggest that the slope of the tangent at Mis -0.4 19 ®) |5a)[(son ) (so. 2)I(s1 2 (= 3) am 2) Co DIEZ) 0.4001 = -0,3999 Point Ly Ly Ly M Ns N: Ni (ev) Stope of Secant |= —0.4082 4) Answers will vary. Section 3.1 Page 128 Question 6 Let the point M represent the population of the small town at 3 years. The coordinates of M are (3, 10 000). Let L be a point on NV = SO00VT-+Fi near M with coordinates (3 + x,5000VT+3-4x or (3 + x, S000VE+x). The slope of 5000V4= x — 10 000 the secant LM can be defined as y = 18000 16000 14000 2000 10000 2000 6000 of 4,6 8 10 L approaches M as x approaches zero. From the table above, the slopes of the secants approach 1250. The value 1250 ‘can be interpreted asthe rate at whic the population is growing with respect to time after 3 years. 3.1 From Secants to Tangents MHR_ 103Section 3.1 Page 128 Question 7 Answers will vay, a) b) Linear regression yields M(H) = 1.017h — 106.457, ©) The slope of the tangent at x = 200 is approximately 1.017, the slope of the line. 4) The Tangent operation returns a result of approximately 1.017, as expected. Section 3.1 Page 129 Question 8 4) The slope of the secant, mpy(x). join 9 cx. /(9)).can be expressed as os os. oy = =” os mel) = oe 02. (@)=0 9 4 gira pa x—2 moa _ fo) w RH) x2 “08 Use (1) and the calculator to determine the slopes of the secant PQ. Dy ma(l.5) = iv) myo(1 8) = as £23 ¥) Mmg(1.9) ipo (2.3) = ) » 23) =f = 9.966 2273 in) 1b) The slopes do not appear to be getting closer to a unique value, from either side of (2, 0). ) Answers may vary 104 MHR. Chapter 3©) To achieve an accurate estimate, values of the x- =) calculator, define Y; = — >. Use the Table feature to display the values on both sides of 2 coordinate of Q must be taken very close to 2. Using (1) and a ‘The slope of the tangent at P(2, 0} is estimated to be approximately ~15.71 or ~Sx. The Tangent operation confirms this result 3.2 Using Limits to Find Tangents Practise Section 32 Page 137 Question 1 9 my 2 LDL m= tin LALO) Section 3.2 Page 137 Question 3 lim L2+D -S¢ ai) Jim + ii ‘The slope of the tangent to f(x) = x*— 4x +5 at 2,1) is 0. 1b) The equation of the tangent at (2, 1) is given by 3 8 yoy smo) 4 ya 1=0(x—2) yo ya yor 2b. y 2 4) Answers will vary. -2 3.2 Using Limits to Find Tangents MHR 105Section 3.2 Page 137 Question 5 For each of the following, let m be the slope of the tangent. a) = lim(x +2), x42 =4 ‘The slope of the tangent at (2,6) is 4 in LOD LD 1 SeT my VeaSa? VEESH2 342 oom x— 1 (Vea 342) = li © Go (Ve=342) 1 x47 = lim 1 T=342 he dpe oft nett. £G) x3 ° I= o- “EGE “IG ya-D iaycr 73 = =-1 The slope of the tangent at (3,1) is ~1 106 MHR Chapter 3 0 n= tin =D 1 to = lim > Bx 1 ote D a+nd st a=) ~U+n = lim 2 x#l The slope of the tangent at (1,1) is ~2,2) The slope of the tangent at (2, -2) is L. Section 32 Page 137 Question 7 4) Determine the slope ofthe tangent, m, at the gen- eral pint (a, a? ~ 8a+ x+a)(x-a)-8(x—a) lime +a-8), x44 1-8 The slope of the tangent at x = ais 2a— 8. h) wl Va@— 1 = lim = _ sl EWE + DWE) ve ‘The slope of the tangent at (1,1) is ‘The slope of the tangent at x = 0 is 2(0)—8 or -8, The slope of the tangent at x = 2 is 2(2)— 8 or —4, iif) The slope of the tangent at x = 4 is 2(4) — 8 or 0, iy) The slope of the tangent at x = 6 is 2(6) ~ 8 or 4 ») 3.2 Using Limits to Find Tangents MHR 107Apply, Solve, Communicate Section 3.2 Page 137 Question 8 4) i) Let m be the slope of the tangent. Determine the equation of the tangent at x = yo f= Mx-2) =x-2 ‘The equation ofthe tangent is y = x. fi) Since the equation of the function and the tan- gent are the same, the requirement that a tangent Touch at only one point is not met, The defini- tion is incorrect, Section 3.2 Page 137 Question 9 a) i) Let m be the slope of the tangent im £- LO) x3 (e+ 3x - 3) Sa xa 3 = lime +3). x #3 =6 ‘The slope of the tangent at (3, 0) is 6. fi) Determine the equation of the tangent at (3,0) y (x = x1) y-0=6(x-3) 6x-18 ‘The equation of the tangent is y = 6x ~ 18. ii) 20: 00 omar) 108 MHR. Chapter3 1b)i) Let m be the slope of the tangent, = tim L-LO =limx?, x40 =0 Determine the equation of the tangent at x = y= £(0) = 0x -0) y-0=0 y=0 ‘The equation of the tangent is y = 0. fi) Since the tangent defined by y = 0 crosses the eubie function, f(x) = x%, at (0,0), the defini- tion is incorrect. b) i) Let m be the slope of the tangent. n= tim 827802) ql 5 Jim (x +2), x #2 ° ‘The slope of the tangent at (~2, ~5) is 0 ii) Determine the equation of the tangent at (2, y= ($5) = 06 =(-2)) yHs=0 ye-s ‘The equation of the tangent is y = -S. iti) 10 8 PBF aS©) i) Let m be the slope of the tangent ¥ x2 = lim(—x - 2), x 42 ‘The slope of the tangent at (2,0) is 4 fi) Determine the equation of the tangent at (2,0) 4x -2) yendr+8 ‘The equation ofthe tangent is y = —4x +8, ii) 4) i) Let mbe the slope of the tangent = limes? 42x44), x #2 =12 ‘The slope of the tangent at (2, 6) is 12 fi) Determine the equation of the tangent at (2,6) y-6= 12-2) y-6=12x-24 y= 12x-18 ‘The equation of the tangent is y = 12x ~ 18. ii) el el | ved | af | a ope 8 3.2 Using Limits to Find Tangents MHR 109©) i) Let mbe the slope of the tangent ‘The slope of the tangent at (2,0) is 12. fi) Determine the equation of the tangent at (2,0) y=0=-I2(x-2) yoni +24 ‘The equation of the tangent is y = ~12x +24. iii) 110 MHR. Chapter3 1) Let mbe the slope of the tangent. m= tim 292) Pyne but is sin EL} tig “i@-D0-y “Miqcna-5 = lim =1 x#2 ‘The slope of the tangent at (2,1) is 1 ii) Determine the equation of the tangent at (2, ~1). yo (C1 = 1-2) yelox-2 yex-3 ‘The equation of the tangent is y iti) 42)i) Let mbe the slope ofthe tangent n= li te 2) VEFE-2 VEFI+2 x=2 Verde xt2-4 The slope ofthe tangent at (2.2) i + ii) Determine the equation ofthe tangent a (2,2). L -2eje-2) ‘The equation ofthe tangent is iti) h)i) Let mbe the slope of the tangent sex tm HOD= ADD Bad stot iT in FD te lime +t txt xe 4 ‘The slope of the tangent at (1,1) is 4. ii) Determine the equation of the tangent at (1,1) ‘The equation ofthe tangent is y ii) 4 3.2 Using Limits to Find Tangents MHR 111Section 3.2 Page 138 Question 10 ) Substitution confirms that (1,1) is on the graph of the function, Let m be the slope of the tangent, Slim 2x-1, x41 The slope of the tangent at (1, 1) is 1. Determine the equation ofthe tangent at (1, 1), yr1=1e-1) yex-14l yex ‘The equation of the tangent is y = x ©) Substitution confirms that (2,3) is on the graph of the function, Let m be the slope of the tangent fim £0) = 802) ia xl SMP yod xoT Saisan “in GG nig teed e—De-D 20-2) “ing=ae-p vine =2 ‘The slope of the tangent at (2,3) is -2. Determine the equation of the tangent at (2, 3), The equation of the tangent is y= —2x +7, 112 MHR Chapter3 1b) Substitution confirms that (0,0) is on the graph of the function, Let m be the slope of the tangent. x2) — 20) im 20=2 = lim[x( = 9), x #0 =0 ‘The slope of the tangent at (0,0) is 0. Determine the equation ofthe tangent at (0,0), y= 0=0(x-0) y=0 ‘The equation of the tangent is y = 0 4) Substitution confirms that (0,—1) is on the graph of the function. Let m be the slope of the tangent. = tim L=LO men xno = lim = = lim wim ettetd =x) “Bias x41) = exes a) xtl x#0 1 The slope of the tangent a (0,~1) is F. Determine the equation of the tangent at (0, -1) yo (1) = 70-0) yet 1 4 1 q 1 1 The equation of the tangent is y = 7x = 1©) Substitution confirms that (4,5) is on the graph of the function, Let m be the slope of the tangent. m= lim LO= LO oe ~F e945 49-25, ayyr e545) oe 4 ~ay(vie +9 +5) tim =D) Ay $945) = tig 2*4 eg 4 The slope of the tangent at (4,5) is 2. Determine the equation ofthe tangent at (4,5). 49 The equation of the tangent is y = 3x + 3 1 Substitution confirms that (4, +) is on the graph of the function. Let m be the slope ofthe tangent tim LLB) re koi ws win SS ae Dave nays lng aaey Tee ae in aaa xe Tea = “IaH The slope ofthecanget at (4,2) i z mine the equation ofthe tangent at (4 1 Bx) 3.2 Using Limits to Find Tangents MHR 113Section 3.2 Page 138 Question 11 4) i) The y-coordinate is y(a) or a, Let m be the _b) i) The y-coordinate is f(a) or a. Let m be the slope of the tangent slope of the tangent. fim = LO) = tim SIOG* tax tary = lim(x? + ax + 4°), xfa s@tata’ =3q* The ope ofthe tangent (a.¢)820,° geste the tangent!) ia i) ermine slope of the tangent at cacl ii) Determine the slope of the tangent at each coordinate = 3(-2)? 2 ma = 3-1 =3 img = 300) =0 im: = 2(0) > =2 m= 300) m= 202) =3 302) 2 fii) As x increases, the slope of the function in- creases linearly, ili) As x increases, the slope of the function de- creases to 0 at x = 0 and then increases, 114 MHR Chapter 3©) i) The y-coordinate is y(a) or a? +2a~ 3. Let m be the slope of the tangent m= lim X= XO) 42x-3-(@ 420-3) Timor +042), x40 satat2 =2a+2 ‘The slope of the tangent at (a, @° +2a—3) is 2a+2 ii) Determine the slope of the tangent at each x-coordinate mg = 2-2) 42 =-442 =-2 m4 = 2-1) +2 =-242 =0 ‘mg = 2(0) +2 =042 =2 my = 21) +2 =242 =4 20) +2 =442 =6 ili) As x increases, the slope of the tangent in- creases linearly, 6 4)i) The y-coordinate is g(@) or —* Let m be the slope 3 ofthe tangent. =n EE) = tim BILE, = DO=3) IIa = aye= 9) tim O02 3) 6(x=3) TG ae e-D 6a— 18 6x +18 = lin Dae = 3) tim a=) sae a3) “Enaraesa 7" 4 “@=3F eee Ce ii) Determine the slope of the tangent at each x-coordinate. 6 ) As x increases, the slope of the tangent decreases as x approaches 3, and then inereases for x > 3. 3.2 Using Limits to Find Tangents MHR 115©) i) The y-coordinateis y(a) or Va? +1. Let me the slope of the tangent, = lim xnav +1 O Veta Vert +1 eel Vert esp of hetangst (, VFI) ie ii) Determine the slope ofthe tangent at each x-coordinate, 2 Vor ili) As x increases, the slope of the tangent increases. 116 MHR Chapter 3 1/1) The y-coordinate is h(a) oF = the slope of the tangent. = tim HDHD +d “Gras Des) tim —@= D049) #2 Gras De sD jim ——+) wre ~(a+a) Srey da “erp ‘The slope of the tangent at 2a @rp ii) Determine the slope of the tangent at cach x-coordinate 2, (Coy 20) RF ‘As x increases, the slope of the tangent in- creases to a maximum of 0.5 at x = =, decreases to a minimum of -0.5 at x = 1, and then approaches 0 as x increases with- ‘out bound. The slope also approaches 0 as x decreases without boundSection 3.2 Page 138 Question 12 Determine the slope of the tangent m with respect to x ata distance m= lima = lim =(-5 = (-5.38 x 10") lim 38 x 10") lim &—# a metres, £69 - f@) me ax(e— a) 38x 10%) tim =}, x #a = (+538 x 10”) (-3) 5.38 x 10" Use (1) in each of the following, 5.38 x 10" (677x107; 17x 10° a “The slope ofthe tangent is approximately 1.17 x 108 5.38 x 10" 65x10" 27x 10° ° ‘The slope of the tangent is approximately 1.27 x 10° Section 3.2 Page 138 Question 13 Let g be the acceleration due to gravity 5 a 5.38 x 10 ox 10F = 124 x 10° ») “The slope ofthe tangent is approximately 1.24 x 10% 5.38 x 10" a ‘The slope of the tangent is approximately 1.32 x 10° 132x 10" 135 000 298 ‘his reslt is similar othe average gravitational force of acceleration atthe surface of the Barth of 9.8 mv? 3.2 Using Limits to Find Tangents MHR 117Section 3.2 Page 138 Question 14 a) ViQ= P39 +10 4) The investor should reinvest ‘of the tangent is 0 2, where the slope inn Y= VO 38 410- (2-3 9 +10) b) Yes. ©) The slope of the tangent att = Os 0. 2is 0. ‘The slope of the tangent at 1) Answers may vary. Section 3.2 Page 138 Question 15 4) The y-coordinate where x = a is »(a) Let m be the slope of the tangent. 1b) The slope of the line y = 14x ~ 6 is 14, m=14 = tin L0=L0) 202 lim(2(x +4) +3), x 4a =2%ata)+3 4a43 x? + 3 is parallel to the line ‘The tangent to y ‘The slope of the tangent at x = ais 4a-+3. Section 3.2 Page 138 Question 16 a x fix) ° x fix) 10 1.001 000 45 x 10"? 0.0001 2.593 742 46 x 107% 1 1.010 045 12 0.000 01 1.104 622 13 x 10-*" OL 1.104 622 13 x 10"! 0,000 001 1.010 045 12 x 10-* 0.01 2.597 742 46 x 107 0,000 000 1 1,001 000 45 x 10-*° ©) Answers may vary. ) Answers may vary. g) Answers may vary, b) limm(x +0.001) =0 18 MHR Chapter3Section 3.2 Page 139 Question 17 a) Let (a, @* + 6a +9) be the point where the tangent haas a slope of 4, Let m be the slope of the tangent. m4 LOS) _ 4 Lx ta atato=4 2a+6=4 ‘The point where the slope of the tangent is 4 is ($1.1 + 6(-1) +9) or (-1,4), Determine the equation of the tangent using the point-slope for- mula yori = m(x— x1) yr 424 (-1) yoda 4x48 ‘The equation of the tangent is y = 4x + 8. b) Let (a, a be the points where the tangent has a slope of 12. Let m be the slope of the tangent. 2 tim LL 2, x#a ‘The points where the slope of the tangent is 12 are (2, 2°) or (2, 8) and (2, (~2)°) or (~2, ~8) Determine the equation of the tangent at (2,8) using the point-slope formula yoy =me— x) y-8=12(x-2) y-8= 12-24 y= l2x-16 y = 12x — 16 is the equation of the tangent at (2,8), Determine the equation of the tangent at (2,-8) using the point-slope formula, ~y=moe—x) (8) = 120-2) yHS=12x+24 y= ltx+16 ‘The equation of the tangent at (~2,—8) is y = 1x +16. 3.2 Using Limits to Find Tangents MHR 119Section 3.2 Page 139 Question 18 Determine the zeros ofthe function, y eox=0 xD =0 x=0,41 a Determine the slope of the tangent, m, at the general point (a, a° ~ a). m= lim LO—LO = in 9 =a -(x-a) a(x? Slime? +ax¢a—1), x¢a Peas =3a-1 @ ‘The slope of the tangent at x = —1 is 3(-1)? — 1 or 2 ‘The equation of the tangent at (~1, 0) is y=0=2(x-(-D) ya2vt2 @ The slope of the tangent at x = 0 is 3(0)* — 1 or —1 ‘The equation of the tangent at (0, 0) is =0=-1(x-0) x 4 y Lor2. The ‘The slope of the tangent at x = 1 is 3(1) equation of the tangent at (1,0) is y-0=2x-1) ys2x-2 a 120 MHR Chapter3 Section 3.2 Page 139 Question 19 ~ 4x) Determine the Lo Let y= 5%? and yp x-coordinates of the points of intersection, rae pit icin ae (-14) a (1.2) Lem beth slope ofthe anget to at = =i LO=L0 = lim = tim 2EOH= 2) Hae a) =lim*** x40 ‘The slopes of the tangents to y; at x = 41 are , respectively. Let m; be the slope of the tangent to y2 at x = a. “Ease + on-a) =” 2G-a) xta slim 7Z2, x ta ata 2 ‘The slopes of the tangents to y; atx = £1 are ‘mz = 1, respectively. At the point of intersection where x = I, since m: xm, = (-1)(1) oF =1, the tangents are perpendicular. At the point of intersection where x = I, since my X mz = (1-1) or =, the tangents are perpendicularSection 3.2 Page 139 Question 20 4) Determine the rate of change of E with respect to x ata distance x = a metres. pa timLD=LO) -*) = (4 10°) im 22 = (-4 10") lim Pa ax@ a) = 4x10") ee =cut) (-4) 4x10 w Determine the radius ofthe orbit of the satelite a = 2(6.38 x 10°) 46.38 x 10° = 1914 « 107 @ Substitute (2) in CD. 4x10” P= Taian oF = 1092 ‘The force of gravity om the satellite is approximately 1092.N b) Result (1) suggests that a increases, the force of gravity decreases. At infinite distances from Earth the gravity becomes infinitesimally small, but it would never be ze. 3.3 The Limit of a Function Practise Section 3.3 Page 153 Question 1 a) kim (3) by lim fx) = 4° ©) lim f(x) = 4) The lim f(x) does not exist because neither the left-hand limit nor the right-hand limit exists at x = 4. ©) lim f(x) = 05 Section 3.3 Page 153 Question 3 a) Jim, g(x) = 12 b) lim g(x) = 1 ©) Tim g(x) 65 eet oxo iets a = 0 mst O tine =9 2b inseoe bioes ” . Him a) = Bim g(x) docs not exist because lim g(x) 4 lim gs). 3.3 The Limit of a Function MAR 121Section 3.3 Page 153 Question 5 a Jip £0) = im = » ‘i f(s) = lim e—3) 1-3 ©) Since lim. (2) = lim, f(x) = ~2, tim f(x) = -2. Section 3.3. Page 154 Question 7 a) ‘ig Hoo) = pg x +2) =042 » Higg RG) = Tim (x ~ 2) =2 ©) Since lim h(x) # lim A(x), lim h(x) does not exis. Section 3.3 Page 153 Question 9 a) lim VF = lim, YT=Ze does not exist 1b) Since fim J7=IR does not exis ©) Since ling be~ 4] = iy fx 4, lim x — 4] = 0. 122 MHR Chapter32 yi al Isl x a » Spy TAR aa limy 1 a 4 By Since tim ly tim Pim does not exist ” V=9 4 EDE-D x-2 x2 » ta yoa =a » Maca oa = lim(x +3), x43 1 a mlm ya XA? a oF P= 6e48 _ 5 (x= DE—4) x42 3) lim = lim G@= BOW 9 = lim, 2+? — a) rm yaa SO DRD = Bed. 44 = lim 2, x24,02-2 =2 wae 8 sim © DEX #2) » s1G=DGx-4) Sx42 Max-a 71 3.3 The Limit of a Function MAR 123x mets 244 ee , 0 Spon ara Ia, 4d = lin, (0? 2844), x #2 = tim te di Bae aad rors) =2 i a k) » Apply, Solve, Communicate Section 33 Page 154 Question 12 a) im, 196) + £00] = f-2) +2) by dim 708001 = s1-2)8(-2) » 6) The limit doesnot exist a it leads tothe square root of a negative number. a lim[/@)-£@)] = [0 - £0 lim £2) _ 10 9 tim = £0 Lim (72) ~ g(0)] = £0) ~ £00) © tin = oO B76) "70 =1-2 1 =2 =-1 “3 1 2 =2 8) The limit does not exis sinee lim f(x) # lim f(x) Gump disomtinty) 1b) The Limit does not exist since lim /(x) does aot exis. fey _ HRI) » B23) 7 Tiga > im £2 EF) Tim FO) x 0 é =3 o Section 3.3 Page 155 Question 13 a) The polynomial 3x + is continuous over its domain, Since lim(3x +1) =7 # 8, fis discontinuous at x = 2 ) Since x +2, x42, and 2x +4 are polynomials, they are continuous over their domains. f is continuous at since lim (v-+2) = lim (x?-42) = 2. fis discontinuous atx = 3 since Jig (x? 42) = 11 and lim (2x44) = 10. ‘and —x are continuous overall real numbers. Since lim x = =1, fis continuous at x oxox 1, f is discontinuous atx =-1. Since ki 4) Since x? ~ 1, x? 2x41, and x? ~ 2x +1 are polynomials, they are continuous over their domains. Since (x2 = 1) = OF and lim (x? +2x +1) = 0%, fis continuous at x = =I, Since lim (x? +2x +1) = 4 and 2x +1) = 0*, Fis discontinuous at x = 1 124 MHR Chapter3Section 3.3 Page 185 Question 14 a) Ma 20 100 CO 4 60 20 Alm’) Section 3.3 Page 185 Question 15 a) cs) meg) Section 3.3 Page 155 Question 16 a) ce 1 (min) B) lim CU) is not defined for a € N because, at each value, the function has a jump discontinuity b) Blip. (A) = 800 fi) fim (A) = 900 ‘img, C(A) does not exist. iv) lim_ (A) = 900 ¥) Jim, c(A) = 1000 Wi) im C(A) does not exist ©) Answers may vary ») i) tim com) = 0.94 fi) lim Com) = 155 iil) lim, Com) does not exist iv) tim, C(m) = 1.55 ¥) lim, Cl) = 2.05 Wi) Jim Cm) does not exis, ©) Answers may vary. Section 3.3 Page 155 Question 17 ce) 5 ox x(km) ‘The discontinuities are at x = is a whole number. 25 + n(0.1) where n, 3.3 The Limit of a Function MHR 125Section 3.3 Page 185 Question 18 Section 3.3 Page 155 Question 19 a a) 1R) = 8+ Ra ~ wa- Ry; R20 ce) rh) ) The discontinuities of C0) are at r= 1,2, and 3. ©) D fim 109 fi) im, 1(R) = iti) 10) fv) Since jim 1(R) 4 Jim 1(R), lim 1(R) does not exist Section 3.3 Page 155 Question 20 a) Jim f(s) = lim 0 =0 Section 3.3 Page 185 Question 21 a) eS 34 Vers (= 9)(34- ver) wi 9=@Fx) (= 9(34 vers) 126 MHR Chapter3(oxy -2 » Baya ee (v8 =2) (V5? +298 +4) _ ae = lim(Vat + 29% +4): x #8 = ed W844 a4aded =12 © im i [ <2 LeVEEe VIER +2 eo [= vias T=VE=x 14Vi=x VT=342 (7-x-4) (1+ VER) = lig <3 — Gx) (VT=e42) G-» (14 Vex) Section 3.3 Page 185 Question 22 Ltx ‘Answers may vary, For example, (3 and g(x) Scetion 33 Page 155 Question 23 For simplicity letx = 2°. Asx > 1, $0, 00, does ¢ > L 3.3 The Limit of a Function MHR 127Section 3.3 Page 185 Question 24 ‘The function f(x) is continuous over all real numbers Section 3.3 Page 155 Question 25 Both (ex ~ 1)? and e? <2 — L are continuous over all real numbers, Check at x = 2, Jim, (0) = lim (ex = 1) = 4-1 For lim f(x) to exist, (Qe= 1) =4e = 82 4c $20 — Bch 8c? 420 = ede —4e# 1) Qe? =0 =0, ‘The function f(x) is continuous over all real numbers if ¢ = O ore 128 MHR Chapter33.4 Rates of Change Apply, Solve, Communicate Section 3.4 Page 168 Question 1 _ay 4) average velocity = 3G +h) -8- BGP -8] 34R3 _3O46h-+ 12) 27 - % 274 18-434 . 7% =1843h, h#0 ‘The average velocity over the interval 1 € [3,3-+ hl is 1843 Section 3.4 Page 168 Question 2 a) The average velocity over the interval € [a, ++] Slath)= fla) # ccan be expressed as Section 3.4 Page 168 Question 3 ai) 32) = -2@)° +32) +1 =-8+641 = a s() = 20)? +30) +1 24341 2 @ On the interval t € [1,2], (2) ~ (1) average velocity = “=o @ Substitute (1) and (2) into (3) Over # ¢ [1,2], the average velocity is ~3 mis. +b) Since wo npg tho 10) jig ZO2B=L) gy Substitute the result from a) into (1). = lim(18 + 3h), #0 =18 ‘The instantaneous velocity at ¢ = 3 is 18, b) The instantaneous velocity at 1 = a can be ex pressed as, instantaneous velocity = fim average velocity Lath) - f(a) ii) a = Q (On the interval 1 € [1, 1.5] _ s(1.5) = s() average velocity = 2 2= 20 8 Substitute (1) and (2) into (3) 1-2 ‘Over # ¢ [1, 1.5] the average velocity is ~2 mals. 3.4 Rates of Change MHR 129iti) sD = 20.1 +30. +1 = 724243341 = 1.88 a s() = -20)' +30) +1 =-24341 =2 @ On the interval f€[1, L.t], _ s(.1)~s() average velocity = “I= 20) 8 Substitute (1) and (2) into (3), 188 “or =-12 ‘Over f€ [1, 1-1} the average velocity is -1.2 mvs » s(L.01) = -2(.01)? + 30.00) +1 = 7204024303 +1 9898 @ sQ) = 20) +30) +1 24341 @ On the interval € (1, 1.01), 3.00) = 50) —— @ ‘Substitute (1) and (2) into (3). 1.9898 ~2 “oor =-102 ‘Over # € [1, 101], the average velocity is ~1.02 m/s Section 3.4 Page 168 Question 4 a) i) (3) = 403) - 4.963 = 120-441 =759 @ y(2) = 402) ~ 4.9(2)" 0 = 19.6 = 604 @ On the interval t € [2,3] average velocity = "2-5 @ Substitute (1) and (2) into (3) 759 - 60.4 ‘Over # € [2,3], the average velocity is 15.5 ms, 130 MHR Chapter 3 iv) =2(1.05)? 4 3(1.05) + 1 -2.205 43.1541 = 1.945 a s() = 2)? +30) +1 -24341 2 @ On the interval f € (1, 1.05}, (1.08) = s() average velocity = @) Substitute (1) and (2) into (3). Over # € [1, 1.05], the average velocity is 1.1 mvs v(t tig Se D= 2 - = tm 2 A= 2 34H BS - = lim ‘The instantaneous velocity at = 1 is —1 mvs i) (2.5) = 40(2.5) —4.9(2.5)° = 100-3002 Loos7s (2) = 40(2) - 4.92)" 198 = 604 Q) onteinerat (223 svengeveecty= 29-1 gy ‘Substitute (1) and (2) into (3) 315-08 nine Over # € [2, 2.5], the average velocity is 17.95 mis,ili) (2.1) = 402.1) 4.92.17 84-21.609 = 62.391 2) = 4002) - 4.9¢2) = 80-196 60.4 On the interval 1 € (2, 2.1]. 2) = yQ) average velocity = ie velocity = "SF Substitute (1) and (2) into (3). 62.391 = 60.4 or 19.91 ‘Over # € [2, 2.1], the average velocity is 19.91 mis ») y(2.01) = 40(2.01) - 4.9(2.01)* = 80.4 - 19,796.49 = 60.603 51 (2) = 40) - 4.92)° = 80-196 = 604 On the interval, € [2,2.01], (2.01) ~ y(2) 201-2 Substitute (1) and (2) into (3) “60,603 $1 - 60.4 “oor = 20351 average velocity = i») (2.08) = 40(2.05) — 4.902 = 82 20.5925 w = 61.407 75 a (2) = 4002) - 4.900) = 80-196 @ 04 a (On the interval r€ [2,2.05], = ¥(2.08) = y(2) @) average velocity = "ZO =H @) ‘Substitute (1) and (2) into (3). 61.407 75 ~ 60.4 0.05 0.155 Over € [2,2.05}, the average velocity is 20.155 m/s 2+) - 92) by) = fim FO 402-48) 492+)? 60.4 @ 3 80 + 40h — 19.6 - 19.6h — 4.9h? - 60.4 a) & (2) m 20.4h - 4.9h? = = lim(204—49h), h #0 @ ene yee =204 ‘The instantaneous velocity at = 2 is 20.4 m/s Over # € [2, 2.01], the average velocity is 20.351 mis. Section 3.4 Page 168 Question 5 a) i) s(4) = 4 46) 45 a s(2) = -27 46(2) 45 3 Site end Gina eas Over # € [2,4] the average velocity is 0 mvs ii) =F 463) 45 941845 reo =M4 a) s(2) = -P +62) 45 441245 @ = @) On the interval #€ [2,31 #3) = s(2) ° average veloity = C= 52) @ Substitute (1) and (2) into 3), 14-13 1 ‘Over # € [2,3], the average velocity is 1 mvs 34 Rates of Change MHR 131a) iii) 2.5? +6(2.5) +5 Tiss 2462) +5 cisites 13 2) onteinerat (223 svengeveniy= I= oy 2B. =o 15 (Over # € [2, 2.5], the average velocity is 1.5 mvs s2+h)= 512) ¥(2) = jim $2 += #2) 1) ¥(2) = fim “= tin TAB? HO A) +S — (2? 460) +5) = lim = 124 6h 44-12 = lim(-h +2). h#0 ‘The instantaneous velocity at f= 2 is 2 mis Section 3.4 Page 169 Question 6 (8) = 53) a) i) average velocity = <= ‘Over € [3,5] the average velo 58.5) =3@) ili) average velocity = Over # € [3, 3.5], the average velocity is 6 5 mvs 132. MHR Chapter3 ivy) s@.1)= 21 462.1) +5 = 441412645 = 13.19 52) =-2 +62) +5 =-441245 =13 (On the interval, € [2.2.1], 52.1) - 52) average velocity = 2-2 Substitute (1) and (2) into (3). _ BI9= 13, Or =19 (Over # € [2, 2.1], the average velocity is 1.9 mvs ° a @ ) 4) The tangent appears in the graph above as the line with arrows at either end, 5) - 3) ii) average velocity = “= 5 (Over # € [3,4], the average velocity is 7 mvs 33.1) = 5) 31-3 _3Pa3 iv) average velocity Over # € [3,3.1], the average velocity is 6.1 mvs») = lino +m), b#0 6 The instantaneous velocity at 1 = 3 is 6 mvs 4) The tangent appears in the diagram as the line with arrows at either end, ©) Answers may vary £) Answers may vary. Section 3.4 Page 169 Question 7 fn + =H i 0.4(a +h)? +S(a th) ~ (04a? 45a) © 07 ‘The velocity at time # = 1is 0.8(1) +5 or 58 mvs The velocity at time 1 = 2s 0,8(2)+5 or 6.6 mvs ‘The velocity at time 1 = 3is 0.8(3) +5 or 74 mus AO.8a+5 404K) = lim BR i Tim(0.8a 454048), b0 =08a+5 ‘The velocity of the car at time t = a is 0.8a++5 metres per second Section 3.4 Page 169 Question 8 For the following solutions, let Fe repesent the average rate of change oftemperature over the closed interval from ' ai) ato T(50) - 730) 30-30 53-65 (p00) = ‘The average rate of change of temperature with respect to time is 0.06 *C/min, 40) - 730) 40-30 57-65 0 -08 TO 0.08 ii) ‘The average rate of change of temperature with respect to time is ~0.08 *C/min, 3.4 Rates of Change MHR 133,G0) - T(10) 30-10 _ 65-12 - 20 =-0275 ‘The average rate of change of temperature with respect to time is ~0.275 °Chmnin, 1b) Answers may vary 35-10 instantaneous rate of change = => ——P 0.1625, Using the approximate endpoints on the tangent (10, 10) and (50, 3.5), the instantaneous rate of change of T at 1-= 30 is approximately —0.16°C/min. Section 3.4 Page 169 Question 9 G0) - 720) » Fam = 68-83 0 -18 To 0.18 ‘The average rate of change of temperature with respect to time is -0.18 *Clmin Tw) 2 1 (50.3.5) For the following solutions, let J.) represent the average rate of change of temperature over the closed interval from tate ai Fan = POO 22 _ 90-50) 4 a 0 ‘The average rate of change of temperature with respect to time is 1.0°Ch. T)-TQ) 422 iti) Tas ‘The average rate of change of temperature with respect to time is 1.15 °Ch, 134 MHR Chapter3 5, 7-70) ii) Toa = TA- TO) ‘The average rate of change of temperature with respect to time is 0.75 "Cih,1b) Answers may vary 1-38 @ 058 Instantaneous rate of change = Using the approximate endpoints of the tangent (0, 3.5) and (6,7), the instantaneous rate of change of T at is approximately 0.58°C/b 1@2)- TAs) on ‘The average rate of change of temperature with respect to time is =1.25°Chh itt) ‘The average rate of change of temperature with respect to time is ~1.15°Ch, Section 3.4 Page 169 Question 10 a) ii) ‘The average rate of change of temperature with respect to time is =1.2°Ch, 4) Answers may vary 37-8 Instantaneous rate of change = "=> 1075 Using the approximate endpoints of the tangent (16, 8) and (20, 3.7), the instantaneous rate of change of T at 18 is approximately —1.08°C/h, 1) For the following solutions, let Nj.» represent the average rate of change in the number of outlets over the closed. interval from ato (199. 1991 — 1984 1984) i) Nusssiso = 500 ~ 200 243 ‘The average rate of change in the number of outlets is approximately 43 outlets per year " (997) ~ N91) » ie = 97 ToT _ 1500 $00 =— S167 ‘The average rate of change in the number of outlets is approximately 167 outlets per year. 3.4 Rates of Change MHR 135(1991) ~ NC1989) 1991 — 1989 500 - 400 2 100 50 ) Nusww.von) ‘The average rate of change in the number of outlets is 50 outlets per year ©) The quadratic regression feature yields an approx imate equation of, N() = 5.6251 ~ 22 2901 + 22 080.000 (1993) ~ (1991) i») youl = F555 —Ta97 700 - 500 _ 200 2 = 100 ‘The average rate of change in the number of outlets is 100 outlets per year 4) Using the regression function determined in part ©), the Tangent operation yields an instantaneous rate of change of 108 outleis per year as compared 3+50-+ 100+ 167 4 the average of oF 90 outlets per year from part b) Section 3.4 Page 170 Question 11 2) For the following solutions, let Pi representthe average at of change in the population over the closed interval fromr= ator =, P(1996) ~ P(1994) 1996 — 1994 423 800 — 416 500 i) Phisee..s961 = 7300 = 3650 e rate of growth of the population is 3650 people per year. P(1998) ~ P1996) 998 = 1996 436 200 — 423 800 iii) Piosesen) = 12.400 = 6200 ‘The average rate of growth of the population is 6200 people per yea. 136 MHR Chapter3 P(4996) ~ P1995) 1996 — 1995 423 800 — 420 100 i) Paresane)— ‘The average rate of growth of the population is 3700 people per year (1997) ~ P(1996) 1997 — 1996 429 800 — 423 800 iv) Prs..9971 000 ‘The average rate of growth of the population is 6000 people per year1b) The points on the tangent drawn at P(1996, 423 800) are (1994, 415 000) and R(1998, 433 000). The slope, m, of the tangent at P can be estimated as follows, +40 000 433.000 — 415 000 —qo98 = 1995 0) 0 «420000 410000 ‘The instantaneous growth rate in 1996 was 4500 people 00000 per year O92 1904 1996 Tome 2000 F ©) The Tangent operation yiclds an instamtancous growth) Averaging the results from pata) yields a growth rate of approximately 4550 people per year in 1996. rate of 4887.5 people per year. 4 ‘The instantaneous rate of change at x = 3 is ~. The tangent is shown inthe graph above 3.4 Rates of Change MHR_ 137Section 3.4 Page 170 Question 13 The volume, V. ofthe erytal with edge length x can be defined by the function V(x) = 3°, Let Vj represent the average rate of change of volume with respect to edge length over the closed interval from x = ao x'=B. a) i) ‘The average rate of change of volume with respect to ‘edge length over the interval x € [4, S]is 61 mm*/mm. ana ity) Fexgoy = SO __ 64.481 201 - 64 01 = 48.1201, ‘The average rate of change of volume with respect to edge length over the interval x € [4,401] is 48.1201 mm*/mm, Section 3.4 Page 170 Question 14 ‘The function can be simplified as follows, 1000 (1-2) -r 000 (&) 1000) Fann 0-8 “i So-n ato) 138 MHR Chapter3 > aD ’ ii) Yuan = 41-4 68.921 ~ 64 Or 9.21 ‘The average rate of change of volume with re- spect to edge length over the interval x € [4,4.1] is 49.21 mm'/mm, 1b) The instantaneous rate of change of volume with respect to edge length when x = 4 is determined as follows. AV vey -Va) aay Ea ee ina (x - 408 + 4x + 16) a = lim(n? + 4x + 16), x 4 = 16416416 =48 ‘The instantaneous rate respect to edge length when x change of volume with is 48 mm'/mm, ‘The instantaneous rate of change at f = 10 can be de- termined. ny Y= VCO) 710 60-18 — § (60 10) ao-na10~2 is SR —7=10 lim -(10-, 1 #10 ‘The instantaneous rate of change of volume with re- spect ta time at = 10s approximately —27.78 L/min,Section 344 Page 170 Question 15 a) i) P(110) = 8000 + 20(110) +0.10(110)* 000 +2200 + 1210 =11410 a) 3000 + 20(100) + 0.10(100) = 8000 + 2000 + 1900 1000 @ Let Fan represent the average at of change of profit with respect to the numberof units produced in the P(100) interval from x = a to x = 8. P(L10) ~ P(100) 110 = 100 6) Poo. = Subsite (1) and (2) int (3) 11410 11 000 = Hato ooo 10 0 a4 Over x € 100,110}. the average profit is $41 iii) P(101) = 8000 + 20(101) + 0.10(101)? 000 +2020 + 1020.1 1040.1 ony P(100) = 8000 + 20(100) + 0.10(100)? 000 +2000 + 1000 1.000 (2) Let Piss represent the average rat of change of prot with respect to the number of units produced from in- terval from x = ato x=, POL) ~ POO) 101 = 100) 6) Poo = Substitute (1) and (2) into (3). 11 040.1 = 11 000 T = 40.1 ‘Over x € {100, 101], the average profit is $40. /unt Section 3.4 Page 170 Question 16 i) P(105) = 8000 + 20(105) + 0.10(105)* = 8000 + 2100+ 1102.50 = 112025 @ ‘P(100) = 8000 + 20(100) + 0.10(100)* = 8000 + 2000 + 1000 = 11000 i) Let Pras represent the average rate of change of profit with respect to the number of units produced from in- terval from x = ato x =. P(105) = P(100) 105 100 Pawo 0s) = @ Substitute (1) and (2) into (3). _ 112025 — 11.000 _ 2025 3 = 405 Over x € {100, 105], the average profit is $40.50/unit 1b) The instantaneous rate of change of profit with re spect to the number of units produced at x = 100 is determined as follows, ar P(x) — P(100) tim 2P = tim POV PAO AE Ax ~My = 100 = gy, 80004 20x + 0.10% — 11 000 sito x= 100 tim 21032 + 20 — 3000 sho x= 100 = ing = 20018 4 30) Mo x — 100 = Jim 0.1430 = 40 ‘The instantancous rate of change of profit with re- spect to the number of units produced at x = 100 is S40/unit 2) Let ¥jaaj be the average velocity in the interval rom f = ato t= b, > 5)=52) 4) Fang = 22 D—@ pas e293 = 40(3) = 0.83(3)* ~ [40(2) ~ 0.83(2)4] 40(2.5) ~ 0.83(2.5)? ~ [40(2) ~ 0.83(2)*] T 0s 20 — 9(0.83) - 80 +.4(0.83) ‘The average velocity over € [2,3] is 35.85 mus [100 — 6.25(0.83) — 80 + 4(0.83)] [20 — 2.25(0.83)] = 36.265 ‘The average velocity over f€ [2,2.5] is 36.265 mvs 3.4 Rates of Change MHR 139iti) jaan = 21-2 4002.1) = 0.8502.) ~ 1402) ~ 08302941 = or = 10{84— 4.41(0.83) ~ 80 + 4(0.83)] = 10/4 0.41(0.83)] = 36597 ‘The average velocity over t€ (2,2.1] is 36.597 mvs 52) 0.83(2.05)" — [40(2) - 0.83(2)*] 0.05 = 20[82 ~ 4.2025(0,83) ~ 80 + 4(0.83)] 20[2 — 0.2025(0.83)] 6.6385 ‘The average velocity over € [2, 2.05] is 36.6385 ms 52.01) ~ 5) ZOl-2 _ 4002.01 83(2.01)? ~ [40(2) ~ 0.83(2)°) 001 = 100[80.4 ~ 4.0401(0.83) ~ 80 + 4(0.83)] = 20{04 - 0.0401(0.83)] 6.6717 ») Fiaz0 ‘The average velocity over r€ [2,2.01] is 36.6717 nus as » v= ig . s2+h)- 51) 20) = ig im 4002 + A) ~ 0.8302 + ‘hy? — 140(2) ~ 0.83(2)"] rr im 402 + A= 2) ~ 0.832 + hy = fy 2244 D- O84 WEF $3[(2 +h- 22 +h+2)) = fy SOE OHI HA DAH HADI im 20% = 0-83h(4 + A) open lim 40 08318 +) 40 -0.83(4) 36.68 ‘The instantaneous velocity at = 2 sis 36.68 mvs, 140 MHR. Chapter3° ¥(@) = fim 22+ = 80) 7 = ting 4002 +A) ~ 0.8300 + A)? [400 ~ 0.830 BR = tiny 4008+ A= 0) ~ 0.8310)? = a] rr = tiny 40h O.831C0+h= alo +h+0)] ims * wg ONCE =ligl40 0832201), h #0 0— 1.660 ‘The instantaneous velocity at ¢~ a seconds is 40 ~ 1.66 metres pe second 4) The projectile will it the moon when = 9 v(a) = 40 = 1.66 ¥(48.193) = 40 ~ 1.66(48.193) =#0,00038 4or= (40-0831) =0 The projectile will hit the moon with a velocity of ap- The projectile was launched at = 0, Determine proximately ~40 mis the other root 40-083=0 40 a8 48.193 “The projectile will hit the surface of the moon at 1 = 48,193 s, {) Determine the time taken to achieve the maximum height. vo=o 40 — 1.661 =0 1.66 = 40 1 = 24.096 ‘The projectile will reach its maximum height at approximately 1 = 24.096, Determine the height at ths instant. s(t) = 401 0.830 5(24.096) = 40(24,096) = 48193 0.83(24.096)" ‘The projectile reaches a maximum height of approximately 481.93 m. 3.4 Rates of Change MHR 141Section 3.4 Page 171 Question 17 4) The position-time graph is depicted below as the dow fim HI ath= oat hea) aE = lim(8 - 2a +h), =2a ‘The velocity-time graph is depicted in the graph by the linear function v(t) = 8 ~ 2 1b) Substitute each value of x into the result obtained in part 2), a) ) 1) The electric force of repulsion ata distance of .0 mis 90 Soy or -22SN 20 fi) The electie force of repulsion a a distance of 10.0 m x iso or -09N, ioe iif) The electric for or ~0.009 N of repulsion at a distance of 100.0 m 100.08 = 90 bs Ste +) 90 ‘The electric force of repulsion between two spheres at a distance of x = xy metres is -—~- newtons ©) Asan cms qian 900 The lest re of pion ta tans o 082 mis ~ 22 225 0OON. ~ €) Siete denon gs end up aste pee ovate a ater pt bt ney te tee gee sal Secion34 Page 11 Question 1 Nu Aten antes lcs i's dean Fer xan all ing wd a poste “actors these al yo Bats a ean ae rely, Te eto als aye 442 MHR. Chapter3Review of Key Concepts 3.1 From Secants to Tangents Section Review Page 173 Question 1 ‘Answers may vary. a) Let Qbe (1+ Ax,(1+Ax)* (1+ Ax) i) Develop a simplified expression for mo ES g itng = 3 AN =o [OD 32122 mg = 222 01 [09.17 3=01=39 Xa7P 0.01 (0.99, 1.9701) = 0.01 = 299 = Uta +4 ax) 2 0001 | 0999, 1997 001) | _3—0.001 = 2.999 I+ax-1 0.0001 | (0.9999, 1.999700) | 3-0,0001 = 2.9999 = Lax + Ant b+ Ann? (0.0001 | (1.0001, 2.000 300)_| 3+ 0.0001 = 3.0001 , oe ‘001 | (1.001, 2.003 001) 340.001 = 3.001 3ax+ (A) aoa oor | (01,2.0301) 3 001= 3.01 =34Axax40 or | a4.23p 3401231 i 1a 3414 ii) From the result of parti), the slope of the tangent at P(1, 2) is estimated to be 3. ii) y Substitute P(x, y:) = (1,2) and m = 3 into (1). = m(x— x b) Let Qbe (2 + Ax, (2+Ax)? 222 Ax) 4) Develop a simplified expression for mo ax Ting = 10+ 6Ax + (Ax)? =10 5 my = 222 =01 _09,3.059) 3a Xoo =0.01 | (1.99,3.900 9.9407 = Gt An? =20 + Ax) 4 0.001 | (1.999, 3.990 00) 9.994 001 tara? , 0.0001 | (4.9999, 3.999 000) 9.999 400 Satie plan san en tannt ‘C.0001 | (2.0001, 4.001 000) 10.000 600 loax +6(a0)? +(y 0.001 _[(2.003, 4.010 006) 10.006 001, ae oor [201,100 601) 10.0601 10+ 6Ax + (Ax)? Ax 40 OF [15.0617 106 101,20) 17 ii) From the results of parti), the slope of the tangent at PCL, 2) is estimated to be 10. Review of Key Concepts MHR 143yor =m(x— x) Substitute P(x, y1) = (2.4) and m = 10 into (1). yo d= 10(x-2) y-4= 10x20 y= 10x—16 ‘The equation ofthe tangent to the curve at Pis y = 10x — 16, @ iy ©) Let Qbe (3+ Ax. STFENFT) 7 ) Let Qhe (3+ Ax. VFFENFT) 7 Q me 4) Develop a simplified expression for mg Var xt? sens =10 | @.173205 0267949 a -0. (29,1974 842) 0251 582 _ vm 34 Ar= Jee ee =001 | 299,197 498) 0250 156 By Varare2 dpaxn4 0001 | 2.999, 1.999 751 0250016 Ax (Vax +2) A ~o.0001 | 2.9999, 1.989075 | 0250002 -— axxo Vem? 10001 | G.0001,2.000025) | 0249998 A From the result of part), the slope of the tangent a1P,2 isesimatedt be 025 jon laoonaowisn | onoe oor | Go1,2.002.498) 0249844 01 | 1.202484) 0248457 10 | 2236068) 0236068 ii) yoy = mo —m) Substitute P(x, 91) = (3,2) and m = 0.25 into y-2=0.25(x-3) fy-82x-3 1 ‘The equation ofthe tangent (o the curve at Pis y = a 144 MHR. Chapter3 xth iy)Section Review Page 173 Question 2 a) i) Use P(O.7, 2.896) and Q(0.6, 2542) ii) Use P(0.7, 2.896) and Q(0.8, 3.233), 2.542 2.896 3.233 - 2.896 me = 3-07 _ 0337 “TI =337 ‘The slope of the secant PQ is 3.54, ‘The slope of the secant PQ is 3.37 1b) Let my represent the slope of thet 3.544337 691 a = 3.455 ‘The slope of the tangent at P(0.7, 2.896) is estimated to be 3.4 ©) i) Use P(L.S, 5.174) and Q(14, 4.937). ii) Use P(LS, 5.174) and Q(1.6, $400), 4937 = 5.174 5.400 - 5.174 ma Tans me = Teas 0.237 _ 0.236 oT “aT 31 = 2.26 ‘The slope of the secant PQ is 2.37, ‘The slope of the secant PQ is 2.26 Let mp represent the slope of the tangent at P 2374226 463 °F = 2315 ‘The slope of the tangent at P(L.S, 5.174) is estimated to be 2.315. 4) Answers may vary. Let two points on the tangent sketched at P(0.7, 2.896) be (0.4, 1.94) and (1.05, 3.95). 395-194 + m= T05—045 ¥ =335 6 5 1 ‘The slope of the tangent at P is estimated to be 3.35. F 174) Let the two points on the tangent at R(15, 5.174) be 4 (11,42) and (19.64) 3 64-42 2 m= Tom ' 78 0S I 1s 208 ‘The slope of the tangent at R is estimated to be 2.75, ©) Answers may vary depending on the method used. The slope of the secant drawn from (0.5, 2.169) to (1.0, 3.859) 3,859 — 2.169 5.174— 3.859 ig SRA 338, The ope of sun dawn om (10,2859) 4 (15,5170 x SHE 3, 10-05 ™ oe oe ‘ , 15-10 2. Aven hepes of hes secant yl meine of 228+ 28 oy. frie dae of he nent at (1.0, 3.859). Review of Key Concepts MHR 145Section Review Page 173 Question 3 4) The slope ofthe function represents the rate at which the body is eliminating the medicine. 1b) The graph below left suggests the slope of the secant cutting A(®) at ¢ = 4 and t = 5 is 2.5 and the slope of the 2544167 secant from f = 3 to 1 = 4 is approximately 4.167, Averaging these results yields an estimate of “= * 7167 gy 3.335. This compares to a result of 3.333 using the Tangent operation of the graphing calculator (below right) TBI TEED pap 070 1050 ©) Answers may vary. 3.2. Using Limits to Find Tangents Section Review Page 174 Question § (=F a) matin LOL 146 MHR Chapter 3 a) Answers will vary bb) The average rate of change from (1937, 11.6) to (1948, 11.5) is 115-116 Toa 1937" ‘The average rate of change from (1948, 11.5) to (1952, 11.4) is 1g 115 or approximately —0.009 s/year. or approximately ~0.025 s/year sep a ‘The average rate of change from (1983, 10.79) to (1984, 10.76) 10.76 10.79 ig OT NOP oy 003 siyear. 1984 — 1983 0.03 sly ‘The average rate of change from (1984, 10.76) to (1988, 10.49) 1049 = 10.76 ig PRA 1O7E op 0.0675 sear. 1988 — 1984 0.0675 sly Averaging these two slopes yields an estimate for the rate of 0.03 ~ 0.0675 change in 1984 of ‘of ~0.048 75 s/year. ‘The slope of the tangent to y Lat (2,5) is 4 yoy mlx — x) yo S=4(x-2) y-S=4x-8 yrarn3 ‘The equation of the tangent is y =») BP ye1 Slime +5), x41 £6) oO meine VEES-3 VEES43 aes Verses 543-9 OEE aE), a ° The slope of the tangent to y = x*-+4x 44 at (1,9) is 6 yoy, = mlx x1) y= 9= 6(x—1) ‘The equation of the tangent is y = 6x +3. 1 ‘The slope ofthe tangent to y = WHS at (6,3) is = yoy sm(x— a1) ‘The slope of the tangent to y = 1 — x? at (0,1) is 0. y= mora x1) O(r= 1) y ‘The equation ofthe tangent is y = 1 The slope of the tangent to y = at (3,1) is yoy = mom) lx-3) ‘The equation of the tangent is y= -x +4. Review of Key Concepts MHR_ 147= lim —— wl VRE +D Section Review Page 174 Question 6 pL = FD a) % * 1th a tim 22+ “heb he = lima +h), h #0 =2 M8 MHR Chapter3 n#l 2 yma mee—x9 f ze ) ey yarpety ‘The equation of the tangent is y = ‘The slope of the tangent to y = 3 — x? at (~1,2) is 2. ‘The equation of the tangent is y = 2x +4. ‘The slope of the tangent to y= x? 2x 41 at (2,1) is. yoy mbx— x1) yo1=2(x-2) yol=2x-4 ys2x-3 ‘The equation of the tangent is y = 2x3.£0 +h) -F0) L om = lim 7 ‘The slope ofthe tangent to y = Va2¥3 at (1,2) is 5 = tm MOEA SS -2 a) i 9 [= 2 ea 3] mo a Vee tb +2 = tim AZAR =A h( vast i +2) ‘The aston ofthe tangent i 2th ago 2 @ lim we? “ER am 1 ral = lim, h#0 ets EB aaew 8 ‘The slope of the tangent to y yoy, = mlx x1) — tn 2D — 44) Pb aKa Dhes—h—d = 18 Sra neo ‘The equation ofthe tangent is y “Ea Review of Key Concepts MHR 149* = tim STI += YG +m? 1 “timo Gane HOA TT =h4+h) PS R@+h 1 4th att neo Section Review Page 174 Question 7 4) i) Let m be the slope of the tangent tim LV=LCD mm x=CD tim @=9P=16 aml = tim 2 OX+9= 16 axel ox-7 aa im @EDA=D res Jim (= 7), x #1 “s ‘The slope of the tangent at (~1, 16) is ~8. ii) Determine the equation of the tangent at (~1, 16) yoy =m(x—m) yn 16=-8x +1) y-16=-8x-8 yo-Brt8 ‘The equation of the tangent is y = —8x +8. ii) 0 BES ETT 150 MHR Chapter3 b) i) Let m be the slope of the tangent, n= tip £0042) )= FQ) Fox bd), x #2 ‘The slope of the tangent at (2, 8) is 12. ii) Determine the equation of the tangent at (2, 8) 12(¢-2) m(x = x1) yr8= 12x24 y= i2x-16 ‘The equation of the tangent is y = 12x — 16. iti)i) Let mbe the slope of the tangent 4) i) Let mbe the slope of the tangent £@)- sa) 5 im c eT m= ting 2 wae 12040) Herp 1 = lim —1 x41 Eh yeas ** 1 ‘The slope ofthe tangent at (11,3) is = fi) Determine the equation of the tangent at (11, 3). yi=m(x=m) -3 do-up a Te sop oftetangenat (4.2) ic fi) Determine the equation of the tangent ‘The equation of the tangent is y = iii) 6 iii) Review of Key Concepts MAR 151Section Review Page 174 Question & a) Let mbe the slope of the tangent Let m be the slope of the tangent. » tim Y=) xta-3,xéa = 2a Tee slpeoftheangen atx = ais24—3, The lope ofthe angen i zen wen 2a = 3 = or when x= 3, The y-coontinate ofthe point is Section Review Page 174 Question 9 4) m= tim YO=YOS) The slope ofthe tangent to y = 2x? ~ Bx + 12 a sons x25 x =2Sis2. Atx = 25, y = 2(2.5)*—8(2.5) +12 2x? — 8x + 12 — (2(2.5)? - 8(2.5) + 12), or 4.5, = Eas yrds = 2x25) = tim SEH 2-20.57 +80.) yr AS = 2x8 = ats x=25 2x05 ots ig, Bate ase ssa The cquon the tegetisy = 25-05 3.3 The Limit of a Function Section Review Page 174 Question 10 a) lim f(a) = 2* by tim, fo = 4) im, f(x) does not exist because. lim. f(x) # lim. (0. ©) lim f(x) by lim fo) & /(S) = Section Review Page 174 Question 11 a) 1) f(x) is discontinuous at x = D lim f(x) = -3" Gump discontinuity), ii) f(x) is discontinuous at x = 2 (removable discontinuity) i) f(x) is continuous at x = 5. ) No, unless the type of discontinuity is known, 182 MHR Chapter3 1) The x-intercept of the tangent in pat a is = or 4. This result would place the skater on a path to the net, so the goaltender should take os)Section Review Page 175 Question 12 a) lim. s() =3" by tim, g(%) = 2* 4) im, g(x) does not exist because im g(x) # lim. g(x) ©) fim 803) 1) lim s(x) = 4" 8) 2) =4, by lim g(x) =4 4) im g(a) = 3* 3) lim s(x) k) a4 D tim g(x) =3 1m) g(5) does not exist (hole) 1) lim g(x) docs not exist since g(x) is not defined for x > 5. Section Review Page 175 Question 13 a) i) g(x) is discontinuous at x = ~3 (jump discontinuity) fi) g(x) is continuous at x = 2 iii) ¢(x) is discontinuous at x = 4 (removable discontinuity) iv) ¢(~) is discontinuous at x = 5 because the function is not defined for x > 5 1b) i) The value of g(a) docs not affect the value of lim g(x), fi) g(x) is continuous at x = a if and only if g(a} im (3). Section Review Page 175 Question 14 a) lim_g(x) = lim (x? +2) -¥ ») dim (6) = tim (44) y ° tim g(x) = 3* Section Review Page 175 Question 15 a) Jim h(x) = Jim (x — 1) _ ») im, (2) = fim (=x +2) 9 Review of Key Concepts MAR 153Section Review Page 175 Question 16 a) Jim lim_(x +3) ») fim, f(x) = lim (x +1) 9 Jim, AG) = 1 Section Review Page 175 Question 17 a) Defining Y; = V7 and using the Table feature of the calculator suggests lim vx ~2 ture ofthe calculator suggests lim b) Defining ¥ = ture of the calculator suggests li x2 +9] and using the Table fea- x +9] =0" 4) Defining Y, ture ofthe calculator suggests lim, |x? +9] = 0° and using the Table fea- Ve 4 =0" 2249] and using the Table fea 154 MHR Chapter3£) Defining Y, = ay singe Te ee of the calculator suggests im k=l w Detning Y=" ns igre ete since tg = |= in Split Screen mode of the graphing calculator doesnot exist” i sven, iy PM = Section Review Page 175 Question 18 b) tim ax? a) lim (4x — 1) = 402) - x +6) = 2G)? 40) +6 = 18-1246 =12 Review of Key Concepts MHR 155by im SE im V3FR-V3 VOFR4+VI s lye von) th 34h lao atin 2th 3 M0 (WSEAS V3) 1 aay = jin nz0 § ie 0 VTE Rt VT , I x Woe ox t4 #4 1 vie=e Ta 4 = Him(12 + 6x + =12 Section Review Page 175 Question 19 2), x#0 4) Since substitution yields a constant other than zero, divided by zero, the limit does not exist =204% » Maas) ees aH) ® =o 8 tim, BT does not exist because the lefthand limit in parte) does not exis. 1b) Examine the left- and right-hand limits separately For x £3, [3- x] =3~—x, hence, Box BB Sox 7 Box PRaTy = lim Lx 43 =I Boal Since Lim in P= x Eas 156 MHR Chapter3 ea © lim tim = DG? AD ©) lim VXFTF does not exist because Vx7427 is ‘nly defined for x > 3. = tim @2DGE*D » sol (x—2)(2x—5) atimXt2) yo 7 = = For y> 3, B—x|=-G— 2), hence, I =~) Mp gox 7 ART = lim -1, x43 Bx ! | does not exist.xsl x+ DOP x41) St = lim yaxpaxy) ext? i) Jim, er Since substitution yields @ constant other than 0, divided by zero, the limit does not exist. 3.4 Rates of Change Section Review Page 176 Question 20 a) i) h(3) = 150 - 4.93)" ii) h(2.1) = 150 - 4.92.1)? = 150 = 44.1 50 ~ 21,609 = 105.9 a 28.391 aw h(2) = 150 — 4.9(2)' ‘A(2) = 150 — 4.9(2)? 150-196 50 - 19.6 104 @ = 1304 @ On he interval f€ (2,3), On the interval f€ (2.2.1 average veloct % average velocity = ©2Y=40) o Substitute (1) and (2) into (3) ‘Substitute (1) and (2) into (3) 105.9~ 1304 128.391 = 1304 os9— 104 H2ss91— 1304 245 09 Over € [2,3] the average velocity is -24.5 m/s (Over {2.2.1}, the average velocity is ~20.09 mis ii) (2.01) = 150 — 4.9(2.01)? b) ¥@) = Jim, 50 — 19.796 49 2+ AN ~ W(2) = 130.203 51 a 2 ar 150 - 4.9(2)? jim 150-492 + AN* ~ (150~ 4.9 = 150-196 Ba 30.4 @ tim = 1+ as? . im, 7 Ontbeinenalr e220) a) hy ARG HAVO AL +2) average velocity = 2 3) Aro Ar ‘Substitute (1) and (2) into (3). = fiml-494 + a0), Ar#0 130.203 51 = 1304 =-196 ~ O01 = -19.649 The instantaneous velocity at = 2is -19.6 mi. ‘Over [2,201], the average velocity is -19.649 mis Review of Key Concepts MHR 157Section Review Page 176 Question 24 gg AP yg PSAP ae Ar amb ar a 41014 ar 99 usb Ar = Him(ar +95), ar eo 93 ‘The rate of change of the population after 5 sis 9.3 bacteria Section Review Page 176 Question 22 a) Eqs 41-1921 _ 34-133 20 i) 0 “20 0,005 ‘The average rate of change in the life expectancy is 0,005 years of life per year, ©) The cubic regression feature yields a cubic func tion with equation 9.85 x 10°x? +0,059x" — 117x +77 400 (5+ AN? 0.715 + AN) + 10~ (S?-0.7¢ 10) ar 1)? = 35 -O7At-25 43.5 ar ) For the folowing solutions, let Eye represent the average rate of change inthe life expectancy over the closed interval from 1 = ato = 6 (961) ~ £00942) 1961 — 1941 _us- D4 ~ 20 Ls oy o7 i) Busan = ‘The average rate of change in the life expectancy is 0,07 years of life per yeas. E(941) ~ E0931) it) Eom THOSE 134-133 7 ol 10 OL ‘The average rate of change in the life expectancy is 0.01 years of life per year. 4) The Tangent operation retums an instantaneous rate of change of approximately 0.041 yeats of life per year_ Averaging the results from past 0.070.008 +001 by) yields SOTF O00 FOF oy approximately 0.0283 years of life per year in 1941 Pee 158 MHR Chapter3Chapter Test Section Chapter Test Page 177 Question 1 a) Ig = 72 by 1-5 3=2 jg MAHA D oe =limo+m), heO -6 ‘The slope of the tangent at Pis 6 9 yay =m x) a ‘The equation of the tangent at Pis y = 6x 7. Section Chapter Test Page 177 Question 2 a) i) Jim £0 = fim Gx -2) ii) stim (3) = =P41 ast fii) Since lim f(x) # lim, (x), lim f(x) does not exis. ©) The polynomial pieces, 3x — 2 and x? + 1, are continuous cover all real numbers. Since lim f(x) # lim f(x), (8) has a jump discontinuity at x = 2, Section Chapter Test Page 177 Question 3 (x 2x8 42x44) “IG DGx+2) . Ba xt2xtd ares 2 oe 3 “2 Chapter Test MHR 1599 Tet algy a 0 Section Chapter Test Page 177 Question 4 ay a) mp = Jim » Axoo Ax = lim 3(1 + Ax)? + S(1+.Ax) +2-10 = 2, ax tim 2188s + 3 (Ax)? +5 +5Ax rd ar Ax(11 434%) a ae = Jim(11+34x), ax #0 =i The slope of the tangent at (1, 10) is 11 ay Ooms hy Rs /3F ax F 1-2 2 ax op VERSE =2 VETER +2 to Ax WERSARGD 443ax—4 so Bx (VE SAR 42) 3 = jim > ax 0 Ames OF ‘The slope of the tangent at (1,2) is 160 MHR. Chapter3 lim sl VRE — DWE +D = lit Al siya * 1 2 » im £2) = S22) tim SEDO? D+ rs? = limy(x? = 2x 44), x A-2 =2 The slope of the tangent at (~2, 0) is 12, 4 (Ax)? ~ 10+ Sax +10 22) Tae Ax(@ax+5) © gr Zax (Ax +2) 4ax+ © geo TAD)" 1 Ax £0 5 a rie seth ge (0)Section Chapter Test Page 177 Question 5 As a) average velocity = 5 1d) + 15) = 8-224 15- (2-11 +15) The average velocity vert € [1,2] is—5 mf As » veo = jm Bt s+ Af) ~ s(1) ¥) = fim ORO P= NG AD + 15= @ay? = Wd) + =m LEAD? = NU + AD + 15= GU)? — HU) +15) is ra om 244A 2A? = Mart 1S 6 = Bs ar ym UCT HBA = ar = Jim -742a1, ar #0 = The instantaneous velocity at = 1is ~7 mis. Section Chapter Test Page 177 Question 6 ‘The formula for the area, A, ofa circle of radius r is A(r) = ar? A(Q0+ Ar) 40) = lim 207 a ar tim 2204 AN? = (20)? =m ‘ar py CO Ar) 208 Sm lit =a jim, 404-Ar = 40% ‘The instantaneous rate of change of area with respect to radius when r = 20 cm is 40x em/em. Chapter Test MHR 161Challenge Problems Section Challenge Problems Page 178 Question 1 The relation xy = 4 can be writen as ay= 4, The general coordinates ofa point P on the function ean be ‘) Determine the slope of the tangent ‘The slope of the tangent at Pis — Section Challenge Problems Page 178 Question 2 Answers will vay, Section Challenge Problems Page 178 Question 3 a) Use Heron's formula to determine Ay, the area of the first island, A 162 MHR Chapter3 Determine the equation of the tangent at P. ‘The x-intercept of the tangent is —= or 2e, ‘There- fore, the coordinates of A are (2c, 0}. The y-intercept ofthe ent is ©. Therefore, the coordinates of B are (0 5) Since the area of AOB ean be expressed as & the areais + x 2c x § or the constant 8, and, there £Bre independeht ofthe poston of point P. ) Since the side length of each smaller triangle is one third the side length of the first island, the area of ceach smaller triangle is one ninth the area of the first island. Let A; represent the area of the second island, 1 Art3 (Ai 1 = Alt 5A i) vv 3 ‘The area of the second island is “> square units a 89©) Since the side length of each smaller triangle is one ninth the side length of the first island, the ratio of the area of each smaller triangle to the area of the first island is 1 : 81. To each of the 4(3) or 12 sides, a smaller triangle is added, Let As represent the area of the third island, (2) v3 v3 Substitute A: = “9 aad ay =F ino 2 a The are of the thie islands “OF square wis 4) The area of the nth island, A,, can be expressed as a series A, 3-44, 440) (2) areata (4) a 5 5Ai+40)(5) ate (5) a+ =A, (: + 3) va Substitute Ay = 2 into 3) -4(+480)) ©) Result (1) fom part d) contains a geomet series in which the common ratio r = 4, Since rl < 1, the series will have a limit, and, so too, will the area, as m gets large. Let A be the limiting value of the area Challenge Problems MHR 163Section Challenge Problems Page 178 Question 4 vaxeT-1 [= (Vax¥T)’ + varoT +1 lim Max (Varv) + Versi 41 _ ax+1-1 Oy (Vax) +Vart1+1 = im ——* x0 8 (Yartl) + vara T +1 "Trist 3 Section Challenge Problems Page 178 Question $ ‘The general equation for an upward-opening parabola with its vertex atthe origin is y = ax*, a > 0, From the position ‘ofthe boat at (~100, 100), the value of a can be identified. yoo w Substitte (xy) = (100, 100) into (1) 100 = a(—100)* 100 = 10 000 l od ‘Tae equation of the path ofthe ski boats y= 2. Determine the slope ofthe tangent othe parabola at tim LVL) =i 1 x = 00 2a Ag a+) 700 Him oe 1 = pp lineta. #6 22 100 30 The sir sould it go ofthe ow ope atthe point F(a, ), whet the slope ofthe tangent othe parabola i ental to the slope of the segment joining P to the dock D(100, 50), a < 100. slope of tangent at P lope of segment PD 00) = AT) (S000} Since 0 < a < 100, the skier should let go of the tow rope at (x,y) = (100 ~ SOV3, 150 ~ 1003) 164 MHR Chapter3Section Challenge Problems Page 178 Question 6 First we argue that the jetpack must be on atthe instant of landing. IFit were not on, then since gravity acts to accelerate the jumper downward, there is no way that the jumper could reach the ground with 0 speed. So the jumper is falling ‘with some speed, and the jetpack goes on at just the right time to slow the jumper down to 0 speed just as she reaches, the ground, ‘When the jumper leaves the helicopter, her speed is 0 and her acceleration is 9.8 mils? downward, When she bits the ‘ground, her speed is 0 and ber acceleration is 44 mvs? upward, Let the height ofthe helicopter be #7. Let the time from when she leaves the helicopter until she turns on the jetpack be f,. Imagine measuring Ayida's time with the jetpack from the ground up. Let the time from when she hits the ground until when she turned on the jetpack be fa From Galileo's law, Ayida will wavel hy = 4.9n* without the jetpack and hs = 2.21? wit the jetpack. Thus, o = 4.9r)? 422n° Ayida’s velocity is given by v = at, of v = 9.87 without the jetpack, and vy = 4.4r with the jetpack. At the moment she tums on the jetpack, these two velocities must be equal. Thus, 9.84, =44h @ Substitute (2) into a) Fora helicopter of height 100 m, 5.60 2514560 Ayida will land after 8.11 b) For a helicopter height of 200 m, +356 ‘Thus, Ayida should tum on her jetpack at ¢ = 3.56 s 98 aa =792 = 3564792 1148 ‘Ayida will land after 11.48 s Challenge Problems MHR 165©) To find the maximum height, determine IT when fp = 10, the maximum time allowed forthe jetpack to be on, 28 iH aa (s#) (#-29()) (522) (osoaa( = 378.78 es ‘The maximum height is approximately 379 m. Using the Strategies Section Problem Solving Page 181 Ques For this purpose, the equator can be assumed to be a circle with circurnference, C, where, nt C=2nr a ‘Adding 1 m to the rope, increases the circumference by 1. Let the new circumference be C”. c=c4l lar tl Q Divide (2) by 2« to reveal the new radius, 7° Cart le le 1 Perey Section Problem Solving Page 181 Question 2 16 moves. Answers may vary. 7-2, 1-6,9-4,6-7,2-9,3-8, 9-4,2-9,4-3. 473,8-1,1-6,3-8,7-2,8-1,6- 166 MHR Chapter3Section Problem Solving Page 181 Question 3 Since all 8 vertices of the cube touch the sphere, the body diagonal of the cube is also a diameter of the sphere. In right AABD, the length of BD can be expressed as Bp = Vid Vi00— a ‘Turning to right ABDC, an equation in x can be determined ‘with the help of (1) and the Pythagorean Theorem, x +x? =(VI00— 3)? 2x? = 100 - x 3x? = 100 @ ‘The volume of the cube is about 192.5 em? Section Problem Solving Page 181 Questi AOPQis a right triangle, Let r be the radius of the inner circle in centimetres. Let A be the area ofthe shaded region in square centimetees. A= Aouter circle ~ Ainner circle =+(V=8) =a? 416-7) = 168 “The area ofthe shaded region is lox em? Section Problem Solving Page 181 Question 5 Since 3 and 5 are factors of 15, the concern is the remainders obtained by dividing 7 by 3 and 5 respectively. When 7 is divided by the 3, the remainder is 1. When 7 is divided by 5, the remainder is 2. The sum of the remainders is 1 +2 or3. Section Problem Solving Page 181 Question 7 a) Drawing three lines yields a maximum of 16 parts suggesting the model Sn + 1 for m lines. 1b) Using the result in part a) suggests that 150 lines will yield 5(150) + 1 or 751 parts 9 Sut l= 116 Sn= 11S n=2B A.maximvum of 116 parts can be achieved with 23 lines. Section Problem Solving Page 181 Question 8 From the fourth point, Dianne and Carys do the same thing, From the third point it ean be concluded then, that Barb behaves differently from both Dianne and Carys, From the fifth point, Erik can’t be swimming because Andrew and Dianne would be swimming, but Barb behaves the same as Andrew but differently than Dianne. It is now apparent that Erik is not swimming. Neither, then, are Andrew and Barb. This leaves Dianne and Carys as the only swimmers. 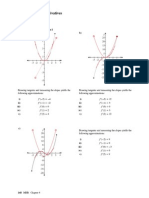Problem Solving-Using the Strategies MHR 167CHAPTER 4 Derivative 4.1 The Derivative Practise Section 4.1 Page 194 Question 1 a) Drawing tangents and measuring the slopes yields the Drawing tangents and measuring the slopes yields the following approximations: following approximations: i Sd 2-4 Dy ii) fDs-2 ii) iti) F@)=0 iti) iv) fed ) ») s£aa4 ») FQ=1 ° Drawing tangents and measuring the slopes yields the {following approximations: i ii 168 MHR Chapter 4