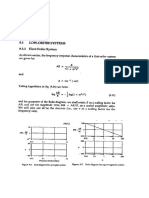
6.1.1 Two Noninteracting Systems in Series Let us, for simplicity, assume a linear relation between liquid level and flowrate through the outlet valves in the system shown in Figure 6.1, so that outflows will be directly proportional to the liquid levels. If A, and Az represent the (uniform) cross-sectional areas of tanks 1 and 2 respectively, then the following mathematical models are obtained by carrying out material balances for each tank © For Tank 1: dhy AV Ge = Fo 6) + For Tank 2 the inflow is given by F, a Ay o = chy eh (62) ‘Tak? Fy Figure 6.1. Two noninteracting tanks in series.& dy ain SP Hy + ete, = KiKi 6a) a second-order differential equation in y,, with u as the forcing function. Transfer Function Model The transfer function representation for the composite system relating y4(s) directly to u(p) is shown in Figure 6.3 and can be obtained by substituting Eq, {65) for y, in Bq, (6.6); the result is: La tel feel cod uo Le. we ee Figure 6.3. Block diagramatic representation of two first-order aystems connected in series, af) = ss) 69 ‘The overall transfer function for this process is therefore now given by: Kika «= Gees D 610) with the characteristic parameters: + K=K,K, the “combined” steady-state gain, + Two time constants, 7, and ¢,, the individual time constants of the contributing first-order elements. ‘The transfer function for this process therefore has two poles (at 5 =-1/r, and 8-1/7) and no zeros. Altematively, we may equally well obtain the transfer function model for this process by laking Laplace transforms of the differential equation model of Eq, (6.8), assuming zero initial conditions. It is an easy task — left as an ‘exercise for the reader — to show that the results are identical. Av ortant point to note here is that the indicated in Eqs. (6.5) and (6.6). A block diagramatic representation of this system shown in Figure 6.3 emphasizes this point.6.1.2 Unit Step Response of the Noninteracting Systems in Series We may now use the transfer function of Eq. (6.9) to obtain expressions for how this system responds to various inputs. When the input function is the unit step function, for example, the system response may be obtained from: x 1 WO) = Garigss Ds (6.11) Since, in this case 4(s) = 1/s. 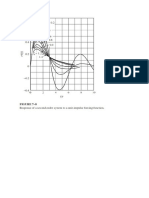Upon partial fraction expansion Eq, (6.11) is easily inverted (provided 1, # 7, )to give: y(t) = «ft - (= & ale - é a Jes] 212) In the special case when 1, = 1, = ¢, Eq, (6.11) becomes: 6.13) -—K_4 WO = Tea Dis and Laplace inversion yields: ~ ett ger) 6.14) v0 = x(19 08 yt) 08 tonks o2 09 ° 2 4 6 8 10 t——_ Figure 6.4. Unit step responses of the liquid level in the two-tank process. A sketch of the two-tank system response is shown in Figure 6.4 and compared with the first-order response behavior of a single tank. ‘The important points to note about these responses are: 1. While the single first-order system response is instantaneous, the response of the two-tank system shows a sigmoidal behavior characterized by an initial sluggishness (at t = 0) followed by a speeding a pee to the final approach to steady state. Note the 2. It is left as an exercise to the reader to show that the SIOpelenine) which is to be compared with the’6.1.3 The Interacting System Let us now consider the interacting system arrangement of Figure 6.2. The material balances for this arrangement are as shown below: For Tank 1: (6.16) For Tank 2: ah, AG © F\-F, GIN