Vector fields associated with first order equations

-2

-2

-4

-4

-6

(a)

-6
-6

-4

-2

(b)

-1

-1

-2

(c)

-4

-2

-2
-2

-1

(d)

-1

-1

-2

(e)

-6

-2

-1

-2

-1

-2
-2

-1

(f)

-2

-2

-4

-4

-6

(g)

-6
-6

-4

-2

(h)

-2

-2

-4

-4

-6

(i)

-4

-2

-6

-4

-2

-6
-6

-4

-2

(j)

-1

-1

-2

(k)

-6

-2
-2

-1

(l)

-2

-1

-1

-1

-2

(m)

-2
-2

-1

(n)

-1

-1

-2

(o)

-1

-2

-1

-2

-1

-2
-2

-1

(p)

-1

-1

-2

(q)

-2

-2
-2

-1

(r)

-1

-1

-2

(s)

-2
-2

-1

(1)
(3)
(5)
(7)
(9)
(11)

f (t, y) = ty
f (t, y) = et
f (t, y) = t2 y 2
f (t, y) = y(y + 1)(y 1)
f (t, y) = ty
f (t, y) = sin y

(13)
(15)
(17)
(19)

f (t, y) = ey
f (t, y) = t2 y
f (t, y) = t2 1
f (t, y) = sin t

(t)
(2)
(4)
(6)
(8)
(10)
(12)
(14)
(16)
(18)
(20)

-2

-1

f (t, y) = sin(y t)
f (t, y) = |y| y
f (t, y) = t y
f (t, y) = y(y + 1)(y 1)
f (t, y) = t2 + y 2 + 1
f (t, y) = y 2 1
f (t, y) = |ty|
f (t, y) = 1 y 2
f (t, y) = sin(t + y)
f (t, y) = t2 + y 2

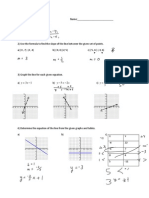
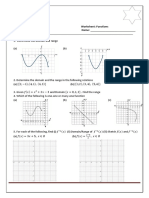
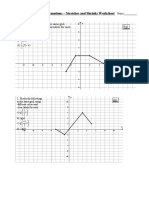
1. Make the correspondence between the expressions and the graphs.

2. For each graph, plot the sketch of some solutions of y 0 = f (t, y).
3. For the vector fields depending only on y draw the correspondent phase line.
4. Find the explicit general solution of the equations y 0 = f (t, y), whenever it is
possible to apply one of the studied methods.