i

EMC 5141 VIBRAES MECNICAS

EM SISTEMAS LINEARES


PARTE 1
Verso 3: 2014







Prof. Roberto Jordan
Departamento de Engenharia Mecnica
Universidade Federal de Santa Catarina
ii

ndice:

Prefcio ........................................................................................................................................ iii

Captulo 1: Sistemas com vrios graus de liberdade ................................................................ 1
1.1 Equaes de Newton - sistemas multi-corpos ........................................................... 1
1.2 Coeficientes de influncia sistemas multi-corpos .................................................. 5
1.3 Respostas livres o problema de valores iniciais ..................................................... 7
1.4 Sistemas com amortecimento no proporcional auto-valores complexos ........... 11
1.5 Sistemas com amortecimento proporcional resposta forada .............................. 13
1.6 Respostas livres (amortecimento no proporcional) o problema
de valores iniciais .............................................................. 16
1.7 Sistemas com amortecimento no proporcional resposta forada ....................... 20

Captulo 2: Sistema contnuos .................................................................................................. 23
2.1 Equao da onda: formulao geral e casos particulares ........................................ 23
2.2 Vibraes livres problemas de autovalores .......................................................... 23
2.3 Vibraes livres problemas de valores iniciais .................................................... 28
2.4 Vibraes foradas .................................................................................................. 30
2.5 Energias cintica e potencial ................................................................................... 32
2.6 Concluso................................................................................................................. 34

Captulo 3: Anlise modal experimental ................................................................................. 35
3.1 Fixao da pea a analisar ........................................................................................................ 35
3.2 Aplicando foras estrutura .................................................................................................... 37
3.3 Aplicao de vibrador ............................................................................................................... 41
3.4 Funes resposta em frequncia sistema de um grau de liberdade .......................... 42
3.5 Funes resposta em frequncia sistema com vrios graus de liberdade ............... 45
3.6 Mtodos de extrao de parmetros modais ....................................................................... 49
3.7 Termos residuais de baixa e alta frequncias ..................................................................... 51

Captulo 4: Mecnica analtica ..................................................................................................................... 54
4.1 Trabalho e energia ...................................................................................................................... 54
4.2 O princpio do trabalho virtual ................................................................................................ 56
4.3 O princpio de dAlembert ....................................................................................................... 58
4.4 As equaes de movimento de Lagrange ............................................................................ 58
4.5 As equaes de movimento de Lagrange para sistemas lineares ................................. 61


Apndice A: Equao da onda seu desenvolvimento para alguns casos fsicos ................ 64
A.1 Vibrao axial em vigas ......................................................................................... 64
A.2 Vibrao torcional em vigas ................................................................................... 67
A.3 Vibrao transversal de cabos sob tenso .............................................................. 70
A.4 Vibrao transversal de flexo em vigas ................................................................ 73
A.5 Propagao de som em dutos (unidirecional) ........................................................ 77


Referncias Bibliogrficas ......................................................................................................... 82

iii


Prefcio:


Esta disciplina optativa do Curso de Engenharia Mecnica da UFSC (EMC 5141
Vibraes Mecnicas em Sistemas Lineares) apresenta alguns tpicos adicionais no estudo de
vibraes, em adio disciplina obrigatria presente no mesmo curso (EMC 5140 Controle de
Vibraes [1]). Consequentemente, esta ltima disciplina funciona como pr-requisito da
disciplina optativa.
No Captulo 1 desta apostila so analisados sistemas do tipo multi-corpos, com vrios
graus de liberdade. So determinadas as frequncias naturais resultantes, modos de vibrao,
respostas livres e foradas.
O Captulo 2 apresenta uma anlise semelhante para sistemas contnuos. Neste caso, ao
invs de serem analisadas vrias equaes diferenciais ordinrias de movimento, como no
Captulo 1, tem-se apenas uma equao diferencial parcial. Um sistema contnuo pode ser
interpretado como um sistema multi-corpos de infinitos graus de liberdade. Assim, este captulo
pode ser entendido como uma extenso do anterior.
Aproveitando as expresses que indicam as respostas foradas de sistemas vibratrios,
desenvolvidas nos dois captulos anteriores, o Captulo 3 fornece uma introduo ao estudo da
anlise modal experimental, que a tcnica que permite encontrar parmetros modais
(frequncias naturais, coeficientes de amortecimento e formas modais) a partir das respostas de
tais sistemas, obtidas experimentalmente.
O Captulo 4 traz uma abordagem completamente diferente, visando obteno das
equaes de movimento de sistemas dinmicos, baseada em grandezas escalares (no vetoriais)
como trabalho e energia. a conhecida mecnica Lagrangeana.
No Apndice A so apresentados os desenvolvimentos da equao da onda
(unidimensional, do ponto de vista espacial) para alguns casos de vibraes em vigas simples,
em cabos tracionados e para a anlise acstica de um duto retilneo.
Em virtude da renovao da disciplina, o contedo complementar ser apresentado
posteriormente.



Roberto Jordan











1

CAPTULO 1: Sistemas com vrios graus de liberdade

So aqui analisados, de forma mais ampla, os sistemas chamados de multi-corpos, ou seja,
aqueles compostos por vrios elementos discretos, como massas, molas e amortecedores. So
descritas a gerao das equaes dinmicas e a consequente obteno das equaes matriciais
para representao dos movimentos [2,3,4,5,6,7,8,9,10]. Surgem ento os problemas de auto-
valores e auto-vetores, que fornecem as frequncias naturais e os modos de vibrao dos
sistemas. Os movimentos livres e forados dos sistemas tambm so estudados.


1.1 Equaes de Newton sistemas multi-corpos

Um sistema multi-corpos, no espao tridimensional (3D), apresenta uma srie de
elementos discretos como corpos rgidos (caracterizados por propriedades de inrcia), molas e
amortecedores. Para se poder descrever a configurao do mesmo, num dado instante de tempo,
necessrio e suficiente que sejam fornecidas as precisas posies de todos os corpos rgidos.
Entretanto, no espao 3D, cada corpo rgido vai possuir seis possveis movimentos: trs de
translao (x, y e z) e trs de rotao (u
x
, u
y
e u
z
). Assim, no havendo restries de movimento,
cada corpo rgido vai requerer seis graus de liberdade (coordenadas temporais) para descrever os
seus movimentos ao longo do tempo.
Para cada movimento do corpo rgido pode-se aplicar a segunda lei de Newton, de forma
a se obter o conjunto de equaes dinmicas:

= x m F
x

u =
x x x
I M

= y m F
y

u =
y y y
I M

(1.1)

= z m F
z

u =
z z z
I M



onde se tm as propriedades de inrcia do corpo rgido, sendo m a sua massa e I
x
, I
y
e I
z
os seus
momentos de inrcia de massa em torno, respectivamente, dos eixos x, y e z.
Em cada uma das equaes acima comum que apaream mais de uma varivel (com suas
respectivas derivadas). Diz-se, assim, que normalmente os movimentos esto acoplados entre
si. Dados n corpos rgidos no espao 3D, tm-se consequentemente 6n graus de liberdade
(incgnitas) e 6n equaes dinmicas, o que permite, como se ver adiante, determinar as
expresses de definio das variveis envolvidas (os graus de liberdade).
Em muitos casos prticos h restries de movimento, de forma que um determinado corpo
rgido pode vir a apresentar um nmero de graus de liberdade inferior a seis. Quando, por
exemplo, se estuda um sistema com um grau de liberdade, e se estabelece que a massa apresenta
apenas um movimento x(t), isto significa que s se permite o movimento de translao em uma
direo, estando os outros movimentos impedidos.
Para ilustrar o procedimento acima discutido, ser analisado o sistema mostrado na
Fig. 1.1, onde h trs corpos rgidos (com massas m
1
, m
2
e m
3
). A tais corpos s permitido o
movimento horizontal de translao, segundo a direo denominada x. Portanto tm-se assim
trs graus de liberdade, um associado a cada massa, representados pelas variveis x
1
(t), x
2
(t) e
x
3
(t). Entre os corpos rgidos, e entre o ponto fixo esquerda e o corpo rgido que lhe prximo,
h elementos discretos de interligao na forma de molas e amortecedores, representados
respectivamente pelas suas constantes de rigidez (k
i
) e de amortecimento (c
i
). A fora
proporcionada pela mola sempre igual constante de rigidez multiplicada pelo movimento
relativo entre os seus extremos. No caso do amortecedor viscoso, aqui adotado, tem-se a
constante de amortecimento multiplicada pela velocidade relativa, tambm entre os extremos.
2

Figura 1.1: Sistema com trs graus de liberdade.

Pode-se portanto aplicar a cada um dos corpos apenas a primeira das Eqs. (1.1), visto que
s h movimento na direo x. Inicialmente analisa-se apenas o movimento livre do sistema, de
forma que no h foras externas aplicadas. Aplicando ento a segunda lei de Newton, na
direo x, a cada um dos trs corpos, so obtidas as equaes:


1
1 1 2 2 1 2 2 1 1 1 1 x
x m ) x x ( c ) x x ( k x c x k F

= + + = ,


2
2 2 3 3 2 3 3 1 2 2 1 2 2 x
x m ) x x ( c ) x x ( k ) x x ( c ) x x ( k F

= + + = , (1.2)


3
3 2 3 3 2 3 3 x
x m ) x x ( c ) x x ( k F

= = ,

que podem ser reescritas na forma:

0 x k x ) k k ( x c x ) c c ( x m
2 2 1 2 1 2 2 1 2 1 1 1
= + + + + ,

0 x k x k x ) k k ( x c x c x ) c c ( x m
3 3 1 2 2 3 2 3 3 1 2 2 3 2 2 2
= + + + + , (1.3)

0 x k x k x c x c x m
2 3 3 3 2 3 3 3 3 3
= + + .

As Eqs. (1.3) podem ser escritas na forma matricial da seguinte maneira:

(
(
(

+
+
+

(
(
(

+
+
+

(
(
(

0
0
0
x
x
x
k k 0
k k k k
0 k k k
x
x
x
c c 0
c c c c
0 c c c
x
x
x
m 0 0
0 m 0
0 0 m
3
2
1
3 3
3 3 2 2
2 2 1
3
2
1
3 3
3 3 2 2
2 2 1
3
2
1
3
2
1

.
(1.4)

As matrizes que aparecem na Eq. (1.4) so as matrizes de massa [M], de amortecimento
[C] e de rigidez [K], respectivamente, para o sistema da Fig.1.1. Todas elas so simtricas e a
matriz de massa , adicionalmente, diagonal. Se o vetor de coordenadas for identificado como
{x} = {x
1
x
2
x
3
}
T
, onde o superndice
T
indica a transposta de vetor ou matriz, pode-se
reescrever a Eq. (1.4) na forma resumida:

} 0 { } x { ] K [ } x { ] C [ } x { ] M [ = + + . (1.5)

Pode-se inicialmente analisar o movimento livre no amortecido do sistema, o que se
obtm considerando a Eq. (1.4) sem a matriz de amortecimento. Para tanto, as coordenadas do
vetor {x} so todas consideradas harmnicas, com a mesma frequncia e, ou seja: x
1
(t) = X
1
e
iet
,
x
2
(t) = X
2
e
iet
e x
3
(t) = X
3
e
iet
. Substituindo estas expresses na Eq. (1.4), lembrando que as
derivadas segundas so dadas por
i
x = - e
2
x
i
, obtm-se a equao:

(
(
(

e
e +
e +
0
0
0
X
X
X
m k k 0
k m ) k k ( k
0 k m ) k k (
3
2
1
2
3 3 3
3
2
2 3 2 2
2
2
1 2 1
. (1.6)
3

A Eq. (1.6) s admite soluo no nula se o determinante da matriz for nulo, ou seja, se a
matriz for singular. Aplicando esta condio, obtm-se a equao:

m
1
m
2
m
3
e
6
[m
1
m
3
(k
2
+k
3
) + m
2
m
3
(k
1
+k
2
) + m
1
m
2
k
3
] e
4
+
[(m
1
+m
2
+m
3
)k
2
k
3
+ (m
2
+m
3
)k
1
k
3
+ m
3
k
1
k
2
] e
2
k
1
k
2
k
3
= 0 . (1.7)

As trs razes da Eq. (1.7) (auto-valores) permitem calcular as frequncias naturais no
amortecidas do sistema da Fig. 1.1. Levando estes valores, na forma quadrtica (e
2
), Eq.
(1.6), possvel obter trs conjuntos de relaes fixas entre as amplitudes X
1
, X
2
e X
3
, que so os
modos de vibrao do sistema (auto-vetores,
1
,
2
e
3
). Os modos indicam um perfil de
amplitudes (forma de vibrar), e no so determinados de forma nica, pois qualquer modo
multiplicado por uma constante continua sendo um modo de vibrao.

Exemplo:

a) Considere o sistema da Fig. 1.1, no amortecido, com todas as massas e molas iguais,
com os valores: m = 79,2 kg e k = 1.10
6
N/m. Levando tais valores na Eq. (1.7) so
obtidas as frequncias naturais: e
1
= 50,0 rad/s, e
2
= 140,1 rad/s e e
3
= 202,5 rad/s.
Levando o valor de e
1
= 50,0 Eq. (1.6), obtm-se:

(
(
(

0
0
0
X
X
X
10 . 802 , 0 10 . 0 , 1 0
10 . 0 , 1 10 . 802 , 1 10 . 0 , 1
0 10 . 0 , 1 10 . 802 , 1
3
2
1
6 6
6 6 6
6 6
, (1.8)

e, adotando-se X
1
= 1,000, chega-se ao auto-vetor correspondente: {1,000 1,802 2,247}
T
.
Repetindo-se o processo para e
2
e e
3
so obtidos respectivamente os auto-vetores
{1,000 0,445 0,802}
T
e {1,000 1,247 0,555}
T
.

A matriz cujas colunas so os auto-vetores do sistema no amortecido permitem
diagonalizar as matrizes de massa [M] e de rigidez [K] do mesmo. Para um sistema de n graus
de liberdade, ter-se-ia ento a matriz de auto-vetores:

[] = [
1
|
2
|
3
| ...... |
n
] . (1.9)

A diagonalizao ento se d da seguinte forma:

[]
T
[M] [] = [diag{
i
g
m }]
e (1.10)
[]
T
[K] [] = [diag{
i
g
k }]

onde [diag{
i
g
m }] uma matriz diagonal, ou seja, aquela que s possui valores no nulos
i
g
m
na diagonal principal, que so os valores das massas generalizadas. Da mesma forma,
i
g
k so
os valores das rigidezes generalizadas. A diagonalizao indica que os auto-vetores
correspondentes a auto-valores distintos so ortogonais quando os produtos so definidos com
relao s matrizes de massa ou rigidez. Matematicamente, isto se expressa na forma:

=
=
=
. j i se , 0
; j i se , m
] M [
i
g
j
T
i
e

=
=
=
. j i se , 0
; j i se , k
] K [
i
g
j
T
i
. (1.11)

4

Pode-se agora realizar uma mudana de variveis, atravs da equao:

{x(t)} = [] {q(t)} , (1.12)

e levar esta expresso Eq. (1.5), na forma no amortecida (matriz [C] nula), o que fornece:

} 0 { } q { ] [ ] K [ } q ]{ [ ] M [ = + + + . (1.13)

Pr-multiplicando a Eq. (1.13) por []
T
, obtm-se:

} 0 { } q { }] k { diag [ } q { }] m { diag [ } q { ] [ ] K [ ] [ } q ]{ [ ] M [ ] [
i i
g g
T T
= + = + + + + + . (1.14)

importante verificar que na Eq. (1.14) as duas matrizes so diagonais. Portanto as
equaes que compem o sistema dependem, cada uma delas, de apenas uma varivel q
i
do vetor
{q}. Em outras palavras, as equaes foram desacopladas e cada uma delas pode ser escrita na
forma:
0 q k q m
i g i g
i i
= + . (1.15)

Consequentemente, se as equaes forem escritas em termos das variveis q
i
, que so
denominadas coordenadas generalizadas, o sistema de n graus de liberdade se apresenta como
se cada um dos n modos fosse um sistema simples e independente de um grau de liberdade, cuja
frequncia natural :

i
i
i
g
g
n
m
k
= e . (1.16)

Os valores de
i
g
k e
i
g
m no so nicos, porque eles so baseados nos auto-vetores,
conforme se pode observar atravs das Eqs. (1.11). Porm a razo entre eles, que define as
frequncias naturais, fixa. Por exemplo, se um dado auto-vetor
i
multiplicado pelo fator
constante o, ambos os valores
i
g
k e
i
g
m sero multiplicados por o
2
, de acordo com as
Eqs. (1.11), e a razo entre eles no se modifica.
Como na Eq. (1.15) no h o termo correspondente ao amortecimento, cada um dos
sistemas independentes teria uma resposta na forma de uma funo harmnica com frequncia
i
n
e , ou seja, na forma
t i
i i
i
n
e Q ) t ( q
e
= , ou ainda na forma de uma senide ou de uma co-
senide. Quando o sistema colocado para vibrar livremente, um determinado modo i pode no
ser provocado, ou seja, ele pode ficar adormecido. Matematicamente, isto se explica tomando-
se a amplitude Q
i
= 0 para aquele modo.
Pode-se agora voltar Eq. (1.12), {x(t)} = [] {q(t)}, cuja interpretao fsica muito
interessante. Abrindo o produto da matriz pelo vetor, o vetor {x(t)} pode ser visto como uma
combinao linear dos modos de vibrao, que so os vetores
i
:

{x(t)} = q
1
(t)
1
+ q
2
(t)
2
+ . . . + q
n
(t)
n
. (1.17)

Portanto a cada instante t o vetor {x(t)} possui, normalmente, uma parcela de cada auto-
vetor
i
. A parcela pode ser maior, menor ou at nula, pois quem fornece o comportamento
temporal de cada modo a correspondente coordenada generalizada q
i
(t), que funciona como
uma funo harmnica de frequncia
i
n
e . Assim, cada coordenada fsica x
i
(t) traz normalmente
embutidas todas as frequncias naturais do sistema. Se um dado modo no for provocado a
vibrar, a sua frequncia no ir aparecer em qualquer das coordenadas fsicas x
i
(t).
5

possvel, neste instante, analisar um tipo especial de amortecimento, denominado
amortecimento proporcional. Ele se caracteriza por apresentar uma matriz de amortecimento
proporcional s matrizes de massa e de rigidez, na forma:

[C] = | [K] + [M] . (1.18)

No difcil perceber que a matriz de amortecimento, assim definida, tambm pode ser
diagonalizada com a ajuda da matriz de auto-vetores:

[]
T
[C] [] = []
T
( | [K] + [M] ) [] = }] c { diag [ }] m k { diag [
i i i
g g g
= + | . (1.19)

Consequentemente, como as trs matrizes (massa, amortecimento e rigidez) so agora
diagonalizveis, a Eq. (1.15) pode ser assim reescrita:

0 q k q c q m
i g i g i g
i i i
= + + , (1.20)

que uma equao equivalente de um sistema de um grau de liberdade amortecido. Portanto
cada coordenada generalizada q
i
(t) vai agora apresentar o comportamento de uma funo
harmnica que progressivamente se extingue (sua amplitude tende assintoticamente a zero).
Do ponto de vista prtico, o modelo de amortecimento proporcional pode ser justificado de
duas maneiras. Seja, inicialmente, por exemplo, o sistema de trs graus da Fig. 1.1. Neste tipo
de montagem, costuma-se admitir que mola e amortecedor atuam sempre em conjunto, formando
uma dupla. Se os coeficientes k
i
e c
i
, para todas as duplas, mantm aproximadamente a mesma
relao numrica, pode-se dizer que a matriz de amortecimento proporcional matriz de
rigidez, ou seja, [C] = | [K] . Em outros tipos de montagem pode acontecer que as foras
dissipativas sejam proporcionais s massas dos corpos rgidos ( o caso de certas foras de atrito,
por exemplo). Em consequncia, pode-se agora admitir que a matriz de amortecimento seja
proporcional matriz de massa: [C] = [M] . Admitindo que os dois fenmenos possam estar
ocorrendo simultaneamente, chega-se Eq. (1.18).

1.2 Coeficientes de influncia sistemas multi-corpos

Na seo anterior, as matrizes de massa, de amortecimento e de rigidez foram obtidas
atravs do estudo das equaes diferenciais dos movimentos do sistema. Esta ltima matriz, de
rigidez, pode tambm ser obtida atravs de outros mtodos, que se preocupam com os
coeficientes de influncia (de rigidez e de flexibilidade), que sero descritos a seguir. Para
descrever estes mtodos, utiliza-se o mesmo sistema que aparece na Fig. 1.1, porm
desconsiderando os amortecedores (a preocupao somente com a rigidez do sistema),
conforme a Fig. 1.2.
Figura 1.2: Sistema de trs graus de liberdade, sem
amortecimento, indicando as foras externas.

Define-se o coeficiente de influncia de flexibilidade a
ij
como o deslocamento no ponto i
(x
i
) causado por uma nica fora unitria, F
j
=1, aplicada no ponto j (onde se tem x
j
).
Com base na Fig. 1.2, pode-se iniciar o processo de determinao dos a
ij
, aplicando de
forma isolada a fora F
1
= 1. Neste caso a mola com rigidez k
1
sofreria um alongamento
x
1
= 1/k
1
, e consequentemente a
11
= 1/k
1
. No havendo foras aplicadas sobre as molas de
6

constantes k
2
e k
3
, os corpos com massas m
2
e m
3
acompanhariam o movimento do corpo de
massa m
1
, logo tem-se a
12
= 1/k
1
e a
13
=1/k
1
.
No segundo passo aplica-se apenas F
2
= 1. Esta fora se transmite atravs das molas com
rigidezes k
1
e k
2
. Em decorrncia, a deformao na primeira delas 1/k
1
e na segunda 1/k
2
.
Portanto o corpo de massa m
1
sofre um deslocamento igual a 1/k
1
(o que fornece a
21
= 1/k
1
) e o
corpo de massa m
2
se desloca de uma quantidade 1/k
1
+

1/k
2
(fornecendo a
22
= 1/k
1
+

1/k
2
).
Finalmente, neste caso, como a mola de constante k
3
no sofre a ao de fora e no se deforma,
o corpo de massa m
3
acompanha o movimento do corpo de massa m
2
, resultando assim o
coeficiente a
23
= 1/k
1
+

1/k
2
.
Como ltimo passo, aplica-se somente F
3
= 1. Agora todas as molas com constantes k
1
,k
2

e k
3
sofrem a ao da fora, apresentando respectivamente as deformaes 1/k
1
, 1/k
2
e 1/k
3
.
Portanto os deslocamentos sofridos pelos corpos de massa m
1
, m
2
e m
3
so, respectivamente,
iguais a: 1/k
1
, 1/k
1
+

1/k
2
e 1/k
1
+

1/k
2
+

1/k
3
. Estes ltimos trs valores correspondem, assim, aos
coeficientes de influncia de flexibilidade a
31
, a
32
e a
33
.
A matriz [a] de coeficientes de influncia de flexibilidade pode ser montada da seguinte
maneira:

(
(
(
(
(
(
(

+ + +
+ + =
(
(
(

=
3 2 1 2 1 1
2 1 2 1 1
1 1 1
33 23 13
32 22 12
31 21 11
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
a a a
a a a
a a a
] a [ . (1.21)

Desta forma, as deformaes estticas causadas por foras constantes quaisquer F
1
, F
2
e F
3

podem ser calculadas por:

(
(
(
(
(
(
(

+ + +
+ + =

3
2
1
3 2 1 2 1 1
2 1 2 1 1
1 1 1
3
2
1
F
F
F
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
1
X
X
X
, (1.22)

ou, em forma resumida, {X} = [a] {F}.
No difcil perceber que a matriz [a] a inversa da matriz de rigidez [K], a qual pode ser
observada na Eq. (1.4), pois para deformaes estticas tem-se {F} = [K] {X}. Assim, se [K]
simtrica, natural que a matriz [a] tambm o seja, o que se percebe na Eq. (1.22).
O sistema da Fig. 1.2 possui restries de movimento, ou seja, ele no est solto no
espao, pois a mola com constante k
1
o conecta a um ponto fixo. Se no houvesse esta
conexo, o sistema, como um todo, poderia sofrer deslocamentos infinitos (como se fosse um s
corpo rgido). Neste caso a matriz de rigidez se tornaria positiva semi-definida, e a sua inverso
se inviabilizaria. A relao direta de inverso, entre as matrizes [a] e [K], fica ento prejudicada
nos casos sem restrio de movimento global.
Os coeficientes de influncia de rigidez so determinados atravs de um procedimento
inverso ao observado para os coeficientes de influncia de flexibilidade. Aplica-se agora um
deslocamento unitrio na coordenada j (onde se tem x
j
) e se mantm as outras coordenadas
zeradas. O coeficiente de influncia k
ij
agora a fora F
i
(aplicada ao corpo onde h a
coordenada x
i
), necessria para manter o sistema nesta situao de deformao descrita
imediatamente acima.
O primeiro passo aplicar, ento, x
1
= 1, x
2
= x
3
= 0, ou seja, apenas o corpo de massa m
1

se desloca para a direita, sendo que os outros permanecem imveis (ver Fig. 1.2). A mola com
7

constante k
1
vai puxar o corpo de massa m
1
com uma fora igual a k
1
.x
1
= k
1
. A mola seguinte,
de constante k
2
, vai empurrar o mesmo corpo com uma fora k
2
.x
1
= k
2
. Portanto a fora total
para a esquerda, aplicada pelas duas molas : k
1
+ k
2
. Assim sendo, a fora total que deve ser
aplicada sobre o corpo de massa m
1
uma fora para a direita (positiva), que corresponde ao
coeficiente k
11
= k
1
+ k
2
. Como a mola de constante k
2
est comprimida, ela empurra o corpo de
massa m
2
para a direita com uma fora igual a k
2
.x
1
= k
2
. Para mant-lo no lugar, em
consequncia, necessrio aplicar uma fora para a esquerda (negativa) de mesmo valor, o que
fornece o segundo coeficiente de influncia k
21
= - k
2
. Finalmente, o ltimo corpo da direita
acaba no sofrendo a ao de fora qualquer, fornecendo k
31
= 0.
O passo seguinte aplicar x
2
= 1, x
1
= x
3
= 0, ou seja, apenas o corpo intermedirio se
desloca para a direita, sendo que os outros permanecem imveis (ver Fig. 1.2). Agora a mola
com constante k
2
tracionada, de forma a puxar o corpo de massa m
1
para a direita, com uma
fora k
2
.x
2
= k
2
. A fora necessria para manter tal massa imvel, ento, uma fora para a
esquerda (negativa) que corresponde a k
12
= - k
2
. Quanto massa m
2
, ela sofre duas foras (uma
de cada lado), ambas para a esquerda, no sentido de lev-la de volta para a posio de equilbrio.
Os valores destas foras so k
2
.x
2
= k
2
e k
3
.x
2
= k
3
. Portanto, a fora que a mantm nesta posio
uma fora para a direita (positiva) equivalente ao coeficiente de influncia k
22
= k
2
+ k
3
. Para
finalizar, deve-se perceber que a mola com coeficiente k
3
est comprimida, portanto empurrando
o corpo de massa m
3
para a direita com a fora k
3
.x
2
= k
3
. Logo, para manter este corpo imvel,
necessria uma fora para a esquerda (negativa) de mesmo valor, o que fornece k
32
= - k
3
.
Para completar a matriz de coeficientes de rigidez, deve-se considerar x
3
= 1, x
1
= x
2
= 0,
ou seja, apenas o corpo de massa m
3
se desloca para a direita, sendo que os outros permanecem
imveis (ver Fig. 1.2). H deformao, neste caso, apenas na mola com constante k
3
, que est
sendo tracionada por uma fora k
3
.x
3
= k
3
. No h qualquer fora aplicada sobre o corpo de
massa m
1
, portanto o coeficiente de influncia correspondente k
13
= 0. O corpo com massa m
2

est sendo puxado para a direita. Para mant-lo no lugar portanto necessria uma fora igual a
k
3
para a esquerda (negativa), fornecendo k
23
= - k
3
. Fechando o exemplo, o corpo de massa m
3

est sendo puxado de volta posio de equilbrio por uma fora para a esquerda. Mant-lo na
posio deformada exige, por consequncia, uma fora para a direita que fornece k
33
= k
3
.
A matriz de coeficientes de rigidez montada finalmente da seguinte forma:


(
(
(

+
+
=
(
(
(

=
3 3
3 3 2 2
2 2 1
33 23 13
32 22 12
31 21 11
k k 0
k k k k
0 k k k
k k k
k k k
k k k
] k [ . (1.23)

Pode-se perceber que a matriz dos coeficientes de influncia de rigidez nada mais do que
a matriz de rigidez obtida atravs das equaes dinmicas do movimento, ver Eq. (1.4).

1.3 Respostas livres o problema de valores iniciais


Quando o sistema multi-corpos no amortecido, tem-se a possibilidade de desacoplar as
coordenadas, sendo que cada coordenada generalizada q
i
vai obedecer uma equao diferencial
igual Eq. (1.15). A soluo desta fornece uma equao do tipo:

) t sen( b ) t cos( a ) t ( q
i i
n i n i i
e + e = , (1.24)

onde as constantes a
i
e b
i
dependem das condies iniciais da funo, em termos de
deslocamentos e de velocidades.
Se for adicionado amortecimento do tipo proporcional ao sistema, a nica diferena que a
Eq. (1.15) deve ser substituda pela Eq. (1.20), onde aparece o novo termo
i g
q c
i
. As trs
8

matrizes (de massa, de amortecimento e de rigidez) podem ser diagonalizadas pela matriz [+], a
mesma matriz de auto-vetores reais obtida para o sistema no amortecido. Tem-se,
consequentemente, como diferena bsica a forma da equao para q
i
(t), obtida agora da soluo
da Eq. (1.20), o que fornece (admitindo o caso sub-amortecido):

| | ) t sen( b ) t cos( a e ) t ( q
i i
i
n i
d i d i
t
i
e + e =
e ,
, (1.25)

onde ) m 2 ( / c
i i i
n g g i
e = , o fator (ou coeficiente) de amortecimento e
i i
n
2
i d
1 e , = e a
frequncia natural amortecida, ambos relativos coordenada generalizada q
i
. Igualmente, na
Eq. (1.25), as constantes a
i
e b
i
dependem das constantes iniciais.
Percebe-se que as funes co-seno e seno tradicionais so trocadas pelas funes co-seno e
seno com decaimento exponencial. Isto ocorre porque se, na Eq. (1.20), admite-se q
i
(t) = Q
i
e
st
,
obtm-se as razes da equao caracterstica associada (auto-valores complexos) dadas pela
expresso:
i i 2 , 1
n
2
i n i i
1 i s e , e , = .
No instante t = 0, com base na Eq. (1.25), tem-se ento:

q
i
(0) = a
i
. (1.26)

Para verificar o que acontece com a derivada temporal de q
i
(t), no instante inicial, seja
determinada inicialmente a sua expresso, derivando-se a Eq. (1.25) com relao ao tempo:

| | ) t sen( b ) t cos( a e ) t ( q
i i
i
n i
i
d i d i
t
n i i
e + e e , =
e ,

| | ) t cos( b ) t sen( a e
i i i i
i
n i
d d i d d i
t
e e + e e +
e ,
, (1.27)

e portanto, para t = 0, tem-se:


i d i n i i
b a ) 0 ( q
i i
e + e , = . (1.28)

Quando no h amortecimento existe apenas uma definio de frequncia natural, e assim,
neste caso, ter-se-ia
i n i
b ) 0 ( q
i
e = .
No caso de um sistema com n graus de liberdade, como a equao dinmica uma equao
diferencial de segunda ordem, devem ser fornecidas as condies iniciais em termos de valores
originais, bem como em termos de suas derivadas temporais. Em outras palavras, no presente
caso necessrio fornecer um perfil de deslocamentos iniciais (o vetor {d
0
}) e um perfil de
velocidades iniciais (o vetor {v
0
}) para se poder definir perfeitamente a condio atual do
sistema, visando determinao do seu comportamento dinmico futuro.
Deve-se, neste ponto, lembrar da Eq. (1.12), que estabelece que {x(t)} = [] {q(t)}.
Substituindo-se t = 0, obtm-se:

{x(0)} = {d
0
} = [] {q(0)} = [] {a} , (1.29)

onde {a} = {a
1
a
2
. . . a
n
}
T
o vetor coluna que rene as constantes a
i
que aparecem nas vrias
Eq. (1.25). Este ltimo vetor citado pode portanto ser calculado como:

{a} = []
-1
{d
0
} . (1.30)

A soluo apresentada na Eq. (1.30) baseia-se na inverso da matriz [], um processo de
fora bruta que apresenta um alto custo computacional para grandes matrizes.
Alternativamente, sugere-se que seja procurada a soluo para a Eq. (1.29) atravs de algoritmos
de soluo de sistemas de equaes lineares.
9

Para tratar do perfil de velocidades, lembrando que a Eq. (1.28) pode ser escrita em forma
matricial, tem-se:

| | } b { }] { diag [ } a { }] { diag [ ] [ )} 0 ( q { ] [ } v { )} 0 ( x {
i i
d n i 0
e + e , + = + = = , (1.31)

onde {b} = {b
1
b
2
. . . b
n
}
T
o vetor coluna que rene as constantes b
i
que aparecem nas vrias
Eq. (1.25). Substituindo a Eq. (1.30) na Eq. (1.31), e buscando isolar-se {b}, obtm-se:

} d { ] [ }] { diag [ ] [ } v { } b { }] { diag [ ] [
0
1
n i 0 d
i i

+ e , + + = e + , (1.32)
ou
} d { ] [ }] / { diag [ } v { ] [ }] / 1 { diag [ } b {
0
1
d n i 0
1
d
i i i

+ e e , + + e = , (1.33)

ou finalmente

} d { ] [ }] 1 / { diag [ } v { ] [ }] / 1 { diag [ } b {
0
1 2
i i 0
1
d
i

+ , , + + e = . (1.34)

A Eq. (1.34) se reduz a } v { ] [ }] / 1 { diag [ } b {
0
1
n
i

+ e = quando no h amortecimento.
Para evitar as inverses de matrizes que aparecem na Eq. (1.34), possvel resolver a Eq. (1.32)
novamente com base em rotinas que tratam de sistemas de equaes lineares.
As Eqs. (1.30) e (1.34) fornecem as constantes que permitem determinar, de forma precisa,
o comportamento temporal de cada uma das coordenadas generalizadas. Uma vez que estas
esto determinadas, a resposta fsica do sistema {x(t)} pode ser calculada com o auxlio de
{x(t)} = [] {q(t)}. Para ficar mais claro, abre-se a seguir esta ltima equao de definio de
{x(t)}:


| | { }
| | { }
n d n d n
t
1 d 1 d 1
t
) t sen( b ) t cos( a e
) t sen( b ) t cos( a e )} t ( x {
n n
n
n n
1 1
1
n 1
e + e +
+ e + e =
e ,
e ,
. (1.35)

A Eq. (1.35) indica que as coordenadas reais do sistema, aglutinadas no vetor {x(t)},
podem ser entendidas como uma combinao linear dos auto-vetores contidos na matriz [+],
onde os multiplicadores so as funes temporais correspondentes s coordenadas generalizadas,
no caso funes seno e co-seno com decaimento exponencial.

Exemplo:

a) Continua-se o exemplo com trs corpos, mostrado na Fig. 1.1, novamente com trs
massas iguais (m = 79,2 kg) e tambm trs molas iguais (k = 1.10
6
N/m). Ele ser
considerado amortecido, com amortecimento do tipo proporcional rigidez, sendo
que a correspondente matriz de amortecimento dada por [C] = | [K], com
| = 0,0005.
A matriz de auto-vetores, j calculados anteriormente, resulta:


(
(
(

= +
555 , 0 802 , 0 247 , 2
247 , 1 445 , 0 802 , 1
000 , 1 000 , 1 000 , 1
] [ . (1.36)
10

Com a matriz [+] acima possvel diagonalizar as matrizes de massa, de
amortecimento e de rigidez, obtendo assim tais grandezas nas formas generalizadas.
As frequncias naturais no amortecidas j haviam sido calculadas (ver exemplo na
pgina 22). Podem agora ser calculados os fatores de amortecimento para as trs
coordenadas generalizadas, cujos valores resultaram em ,
1
= 0,0125, ,
2
= 0,0350 e
,
3
= 0,0506.
So agora fornecidas condies iniciais ao sistema atravs dos seguintes
vetores de deslocamentos {d
0
} e de velocidade iniciais {v
0
} arbitrrios:

=
0 , 3
5 , 2
8 , 1
} v { e
035 , 0
018 , 0
016 , 0
} d {
0 0
. (1.37)

Aplicando as Eqs. (1.30) e (1.34) obtm-se os vetores:

=
0124 , 0
0070 , 0
0088 , 0
} b { e
0202 , 0
0109 , 0
0067 , 0
} a { . (1.38)

Podem ser determinados agora os comportamentos temporais das coordenadas
generalizadas q
1
(t), q
2
(t) e q
3
(t), com o auxlio da Eq, (1.25), os quais esto
mostrados na Fig. 1.3.


Figura 1.3: Comportamento temporal das
coordenadas generalizadas q
1
(t), q
2
(t) e q
3
(t).

Percebe-se, na Fig. 1.3, que cada coordenada generalizada possui simplesmente
um comportamento harmnico com decaimento exponencial (uma s frequncia
natural amortecida).
Na Fig. 1.4 esto mostrados os comportamentos das coordenadas reais, x
1
(t),
x
2
(t) e x
3
(t), obtidas com o auxlio de {x(t)} = [] {q(t)}.
11


Figura 1.4: Comportamento temporal das
coordenadas reais x
1
(t), x
2
(t) e x
3
(t).

Pode-se observar que, em cada curva da Fig. 1.4, h uma combinao de
funes harmnicas com decaimento exponencial, pois em todas elas h a
participao dos trs modos de vibrao (representados por suas respectivas
coordenadas generalizadas).

1.4 Sistemas com amortecimento no proporcional auto-vetores complexos


Seja rescrita a equao da dinmica de um sistema multi-corpos amortecido:

} 0 { } x { ] K [ } x { ] C [ } x { ] M [ = + + . (1.39)

Na Seo 1.1 verificou-se que se no h amortecimento ([C] = [0]) os auto-valores
apresentam-se na forma
i
n
i e , onde
i i i
g g n
m / k = e . Neste caso h uma matriz de auto-
vetores reais [+] que permita a diagonalizao das matrizes [M] e [K]. Quando o amortecimento
do tipo proporcional, verificou-se na Seo 1.3 que os auto-valores aparecem em pares
complexo-conjugados na forma:
i i
n
2
i n i
1 i e , e , , sendo que a mesma matriz [+]
permite a diagonalizao de todas as matrizes que aparecem na Eq. (1.39).
Se o amortecimento do tipo no proporcional, no existe mais uma matriz de auto-
vetores reais que permita a diagonalizao de todas as matrizes, com o consequente
desacoplamento das coordenadas generalizadas.
Tanto os auto-valores como os auto-vetores aparecem agora normalmente em pares
complexo-conjugados. Para determin-los, admite-se que possa haver uma soluo envolvendo
uma funo na forma {x(t)} = {X}e
st
, onde s uma varivel complexa. Substituindo esta
expresso na Eq. (1.39) obtm-se:

( ) } 0 { } X { ] K [ ] C [ s ] M [ s
2
= + + . (1.40)
12

A Eq. (1.40), pelo fato de se apresentar na forma de um sistema de equaes homogneas,
s admite uma soluo no nula se o determinante da matriz entre parnteses for nulo, ou seja, se
esta matriz for singular. Se o vetor {x(t)} possui n coordenadas reais, anulando-se o
determinante da matriz chega-se a uma equao polinomial de grau 2n em s. Como os
coeficientes de tal equao so reais, as 2n razes (auto-valores) s podem ser reais ou complexo-
conjugadas. Para sistemas com amortecimento no extremamente elevado, obtm-se somente
valores complexo-conjugados, os quais fornecem a conhecida caracterstica de movimento
harmnico com amplitude decrescente quando os sistemas esto sob vibrao livre. Levando as
razes (auto-valores) de volta Eq. (1.40) possvel encontrar os correspondentes auto-vetores,
da mesma forma que foi feito na Seo 1.1. A grande diferena, entretanto, que agora os auto-
vetores aparecem tambm em pares complexo-conjugados, correspondendo a pares de auto-
valores complexo-conjugados.

Exemplo:

a) Seja o sistema de dois graus de liberdade da Fig. 1.5.


Figura 1.5: Sistema com dois graus de liberdade.

As correspondentes matrizes de massa, de amortecimento e de rigidez so:

(

+
=
(

=
(

=
2 2
2 2 1
2 2
2 2
2
1
k k
k k k
] K [ e
c c
c c
] C [ ,
m 0
0 m
] M [ . (1.41)

importante perceber que este no um caso de amortecimento proporcional, pois
se o fosse deveria haver um amortecedor com constante c
1
em paralelo com a mola de
constante k
1
. Alm disso, a relao c
1
/k
1
deveria ser igual relao c
2
/k
2
, para permitir
que as matrizes [C] e [K] estivessem relacionadas apenas por uma constante de
multiplicao.
So adotados os valores m
1
= m
2
= 100 kg, c
2
= 200 Ns/m e k
1
= k
2
= 1.10
6
N/m.
Levando todas estas informaes Eq. (1.40) e igualando o determinante a zero, obtm-
se a equao polinomial:

1.10
4
s
4
+ 4.10
4
s
3
+ 3.10
8
s
2
+ 2.10
8
s + 1.10
12
= 0 , (1.42)

cujas razes fornecem os valores (-0,11 i 61,8) e (-1,89 i 161,8). Estes auto-vetores se
apresentam como dois pares complexo-conjugados, como esperado. As partes reais so
ambas negativas, como no poderia deixar de ser, pois assim as funes exponenciais
obtidas tendem progressivamente a zero. Os correspondentes auto-vetores complexos,
com dois elementos, se revelaram da seguinte forma: {1,000 (1,618 - i 0,009)}
T
,
{1,000 (1,618 + i 0,009)}
T
, {1,000 (-0,618 - i 0,009)}
T
e {1,000 (-0,618 + i 0,009)}
T
.
Todos os auto-vetores foram determinados admitindo-se que o elemento da primeira
posio (superior) fosse igual unidade, com os demais elementos (inferiores) sendo
determinados em decorrncia deste fato.

13

1.5 Sistemas com amortecimento proporcional resposta forada


Voltando equao da dinmica de um sistema multi-corpos amortecido, agora com a
aplicao de foras externas (vetor{f}), tem-se:

} f { } x { ] K [ } x { ] C [ } x { ] M [ = + + . (1.43)

A anlise que ser realizada a seguir procura levantar as funes resposta em frequncia de
sistemas com amortecimento do tipo proporcional, de forma semelhante quela que normalmente
empregada para sistemas de um grau de liberdade (resposta forada). O resultado, portanto,
estabelece as relaes entre as amplitudes das foras aplicadas e as consequentes amplitudes de
movimento do sistema, como funes da frequncia e.
Outra anlise possvel seria a determinao de respostas temporais do sistema, quando lhe
so aplicadas foras externas. Se fosse seguido este procedimento, para sistemas com
amortecimento, tais respostas mostrariam uma regio inicial composta de duas parcelas, uma de
resposta livre (com o sistema vibrando de acordo com as suas frequncias naturais amortecidas)
e outra de resposta forada (com o sistema vibrando de acordo com as frequncias imposta pelas
foras externas). Passado algum tempo, as respostas livres se extinguiriam pela ao do
amortecimento, e sobraria apenas a resposta forada, em regime permanente. exatamente esta
resposta em regime permanente que se vai conseguir atravs da anlise a seguir, em termos de
relaes de amplitudes como funes de frequncia.
Vai-se admitir aqui uma restrio em termos de foras, pois, apesar da possibilidade de
aplic-las em qualquer corpo do sistema, elas sero admitidas todas com a mesma frequncia, ou
seja, tem-se o vetor de foras externas {f} = {F} e
iet
. Em consequncia, como o sistema
linear, as respostas tambm apresentam o mesmo comportamento, ou seja, {x} = {X} e
iet
.
Levando estas expresses Eq. (1.43), eliminando o termo e
iet
, obtm-se:

} F { } X { ] K [ } X { ] C [ i } X { ] M [
2
= + e + e . (1.44)

Como o sistema apresenta amortecimento do tipo proporcional, as matrizes [M], [C] e [K]
podem ser diagonalizadas pela matriz de auto-vetores reais [+], obtidas a partir da anlise do
sistema no amortecido (ver Seo 1.1). Para poder aproveitar esta propriedade, adota-se a
seguinte mudana de variveis:
{X} = [+] {Q} , (1.45)

onde {Q} o vetor de amplitudes de coordenadas generalizadas.
Substituindo a Eq. (1.45) na Eq. (1.46), chega-se a:

} F { } Q { ] [ ] K [ } Q { ] [ ] C [ i } Q { ] [ ] M [
2
= + + + e + + e , (1.46)

a qual ento pr-multiplicada por [+]
T
:

} F { } F { ] [ } Q { ] [ ] K [ ] [ } Q { ] [ ] C [ ] [ i } Q { ] [ ] M [ ] [
q
T T T T 2
= + = + + + + + e + + + e , (1.47)

sendo {F
q
} o vetor das foras generalizadas.
Na Eq. (1.47) as matrizes [M], [C] e [K] resultam diagonalizadas, e portanto cada linha
desta equao se apresenta na forma:


i i i i
q i g g g
2
F Q ) k c i m ( = + e + e , (1.48)
ou

i
i i i
q
g g g
2
i
F
k c i m
1
Q
+ e + e
= . (1.49)
14

ou ainda, finalmente:
i i i i
g g g
2
q
i
k c i m
1
F
Q
+ e + e
= . (1.50)

Observando-se a Eq. (1.50) possvel perceber que para cada coordenada generalizada Q
i
,
que representa um modo de vibrao, tem-se o comportamento semelhante ao de um sistema de
um grau de liberdade (massa, amortecedor e mola) sob a ao de fora externa, pois tal equao
semelhante equao X/F = 1 / (-e
2
m + i e c + k), que corresponde quele sistema simples.
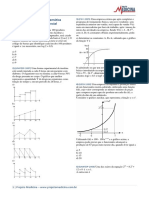
Cada Eq. (1.50), em mdulo, fornece uma curva conforme a Fig. 1.6 abaixo, com um
mximo aproximadamente na frequncia
i i i
g g n
m k = e .
Figura 1.6: Mdulo da relao fornecida pela Eq. (1.50).

As vrias Eqs. (1.49) podem ser reunidas numa s equao matricial, fornecida a seguir:

} F {
k c i m
1
diag } Q {
q
g g g
2
i i i
(

)
`

+ e + e
= . (1.51)

Lembrando que {X} = [+] {Q} e que {F
q
} = [+]
T
{F}, a Eq. (1.51) se transforma em:

} F { ] [
k c i m
1
diag ] [ } X {
T
g g g
2
i i i
+
(

)
`

+ e + e
+ = . (1.52)

Devido ao desacoplamento dos modos, a Eq. (1.52) permite perceber que cada amplitude
de resposta X
i
, como uma funo da frequncia, vai conter, a princpio, vrios picos de
ressonncia, em torno das vrias frequncias naturais
i
n
e . Ou seja, a funo resposta em
frequncia aparece como a soma de vrias funes individuais, uma correspondente a cada modo
de vibrao.

Exemplo:

a) Seja o exemplo com trs graus de liberdade j estudado na Seo 1.3, mostrado na Fig. 1.1.
As massas so todas iguais (79,2 kg), as molas tambm (1.10
6
N/m) e a matriz de
amortecimento proporcional matriz de rigidez ([C] = | [K]), com | = 0,0005.
15

A matriz de auto-vetores reais [+], calculada na Seo 1.1 sob a hiptese de sistema
no amortecido, dada na Eq. (1.36). Ela permite calcular os parmetros generalizados, o
que forneceu, respectivamente para os modos de 1 a 3, os valores: massas generalizadas =
736,2; 145,8 e 226,7 kg; coeficientes de amortecimento generalizados = 0,921.10
3
;
1,431.10
3
e 4,648.10
3
Ns/m e constantes de mola generalizadas = 1,841.10
6
; 2,863.10
6
e
9,296.10
6
N/m. As frequncias naturais no amortecidas apresentam, tambm
respectivamente, os valores j determinados na Seo 1.1: 50,0; 140,1 e 202,5 rad/s.
Levando tais valores Eq. (1.50) so obtidas as trs curvas mostradas na Fig. 1.7, onde as
frequncias de ressonncia (picos) correspondem aos ltimos valores apresentados acima.
Figura 1.7: Valores de | F / Q |
i
q i
para: a) a primeira coordenada
generalizada; b) a segunda e c) a terceira.

Neste exemplo ser aplicada apenas uma fora harmnica na massa m
2
(correspondente coordenada x
2
) com o valor de 10.000 N, ou seja, o vetor de amplitudes
de fora fica na forma: {F} = { 0 10.000 0}
T
. Aplicando agora a Eq. (1.52) so obtidas as
amplitudes resultantes do movimento (vetor {X}) como funes da frequncia, cujas curvas
(em mdulo) esto mostradas na Fig. 1.8.

Figura 1.8: Respostas em frequncia |X
1
(e)|, |X
2
(e)| e |X
3
(e)|.

Percebe-se, principalmente atravs da anlise dos picos, que as curvas da Fig. 1.8 so
combinaes das curvas que aparecem na Fig. 1.7.
16

1.6 Respostas livres (amortecimento no proporcional) o problema de valores iniciais

Seja um sistema multi-corpos representado por suas matrizes de massa [M], de
amortecimento (no proporcional) [C] e de rigidez [K]. Considerando-se que ele possua n graus
de liberdade, tais matrizes possuem dimenses nn. Aplicando ao mesmo a segunda lei de
Newton, admitindo movimento livre (sem fora externa aplicada), obter-se-ia:

} 0 { } x { ] K [ } x { ] C [ } x { ] M [ = + + . (1.53)

Neste caso, como o amortecimento no do tipo proporcional, no podem ser
diagonalizadas as trs matrizes citadas acima atravs de uma simples mudana de variveis.
necessrio, agora, trabalhar com um sistema de equaes de ordem dupla, ou seja, com 2n
variveis em lugar do tradicional vetor {x} com n variveis. Isto obtido tomando-se o vetor
{y} na forma:

=
) t ( x
) t ( x
)} t ( y {

. (1.54)

Adotando esta alterao, a Eq. (1.53) pode ser escrita como:

| | } 0 { } y { ] 0 | K [ } y { M | C = + , (1.55)

onde o elemento 0 dentro da matriz representa uma matriz nula, com dimenses iguais s das
matrizes [M], [C] e [K], e o vetor {0} o vetor coluna nulo com 2n posies.
Para se poder trabalhar com matrizes quadradas, escreve-se a equao auxiliar, trivial,
fornecida abaixo:
| | } 0 { } y { ] M | 0 [ } y { 0 | M = + . (1.56)

Fundindo-se as Eqs. (1.55) e (1.56), obtida a equao matricial:

} 0 { } y {
M 0
0 K
} y {
0 M
M C
=
(

+
(

, (1.57)

que, em forma reduzida, pode ser apresentada assim:

| | } 0 { } y { ] B [ } y { A = + . (1.58)

Como so esperados auto-valores e auto-vetores complexos, admite-se uma soluo na
forma {y(t)} = {Y} e
st
. Levando esta ltima expresso Eq. (1.58), obtm-se:

[sA + B] {Y} = {0} . (1.59)

Para que a Eq. (1.59) admita solues {Y} no nulas, o determinante da matriz [sA + B]
deve ser nulo. Aplicando esta condio obtida uma equao polinomial em s, de ordem 2n,
cujas razes fornecem os auto-valores s
i
. Como os valores nas matrizes [A] e [B] so reais, os
coeficientes no polinmio tambm o so, e consequentemente as razes s podem ser nmeros
reais ou complexo-conjugados. Para sistemas com baixo amortecimento, normalmente so
encontrados n pares complexo-conjugados, na forma:
i
s e
*
i
s .
Levando os auto-valores Eq. (1.59) podem ser determinados, de forma semelhante j
detalhada anteriormente, os auto-vetores correspondentes, que tambm so complexo-
conjugados: } {
i
u e } {
*
i
u .
17

Estes vetores so admitidos como colunas da matriz [], a exemplo do que foi feito na
Seo 1.1. A matriz [], cujos valores so complexos, mais o seu par complexo-conjugado [
*
],
permitem diagonalizar as matrizes [A] e [B]:

[
*
]
T
[A] [] = [diag{a
i
}] e [
*
]
T
[B] [] = [diag{b
i
}] . (1.60)

Adota-se a mudana de variveis:

{y} = [] {p}, (1.61)

e portanto agora a Eq. (1.58) pode ser assim escrita:

| | } 0 { } p { ] [ ] B [ } p { ] [ A = O + O , (1.62)

a qual, pr-multiplicada por [
*
]
T
, se transforma em:

| | } 0 { } p { ] [ ] B [ ] [ } p { ] [ A ] [
T * T *
= O O + O O . (1.63)

Obteve-se, atravs da Eq. (1.63), a diagonalizao das matrizes [A] e [B]. Cada linha
ento fornece:
0 p b p a
i i i i
= + . (1.64)

Como
i i i
p s p = , tem-se:
(a
i
s
i
+ b
i
) p
i
= 0 , (1.65)

o que confere a cada auto-valor a relao:

i
i
i
a
b
s = . (1.66)

A equao diferencial (1.64) possui como soluo a expresso, para cada i-sima
coordenada p
i
:

t s
i i
i
e c p = , (1.67)

onde as vrias constantes c
i
, como se ver adiante, so determinadas a partir das condies
iniciais do problema.
Pode-se, neste momento, interpretar a Eq. (1.61) como se o vetor {y} fosse uma
combinao linear dinmica dos auto-vetores:

} { e c } { e c } { e c } { e c } y {
*
n
t s *
n n
t s
n
*
1
t s *
1 1
t s
1
*
n n
*
1 1
u + u + + u + u = . (1.68)

Na Eq. (1.68) os termos sempre ocorrem em pares complexo-conjugados, de forma que o
vetor resultante {y} apresenta valores reais. E no poderia deixar de ser assim, uma vez que ele
contm em sua composio os valores de n deslocamentos e n velocidades, que apresentam
valores reais.
No tempo t = 0 so fornecidas as condies iniciais x(0) = x
0
e
0
v ) 0 ( x = . Ento, com o
auxlio das Eqs. (1.61) e (1.68), para t = 0, obtm-se:

{y(0)} = [] {p(0)} = [] {c} =

0
0
v
x
, (1.69)

onde o vetor coluna {c} dado por
T *
n n
*
1 1
} c c c c { .
18

Da Eq. (1.69) pode ser obtida uma expresso para clculo das constantes c
i
:

{c} = []
-1

0
0
v
x
. (1.70)

Uma questo muito importante sobre a Eq. (1.70): se o sistema permitir movimentos de
corpo livre, isto , se o mesmo no estiver devidamente amarrado, podem aparecer auto-
valores nulos e consequentemente auto-vetores idnticos. Neste caso a matriz [] se torna
singular (com determinante nulo), e portanto a sua inversa []
-1
no existe. Fisicamente, o
problema seria determinar a resposta de um sistema que est solto no espao a condies
iniciais, o que normalmente o leva a respostas com amplitudes infinitas.
O vetor de coordenadas modificadas {p} pode ser escrito como:

} c { }] e { diag [ } p {
t s
i
= , (1.71)

e, com o auxlio da Eq. (1.61), tem-se:
{y(t)} = [] }] e { diag [
t s
i
[]
-1

0
0
v
x
. (1.72)

Exemplo:

a) Seja o mesmo sistema com dois graus de liberdade, com amortecimento no proporcional,
da Seo 1.4, cuja figura novamente mostrada abaixo.


Figura 1.9: Sistema com dois graus de liberdade.

So adotados os mesmos parmetros para o mesmo: m
1
= m
2
= 100 kg, c
2
= 200
Ns/m e k
1
= k
2
= 1.10
6
N/m. As matrizes [A] e [B], de acordo com as Eqs. (1.57) e
(1.58), so ento dadas por:


| |
(
(
(
(

=
0 0 100 0
0 0 0 100
100 0 200 200
0 100 200 200
A
e
| |
(
(
(
(

=
100 0 0 0
0 100 0 0
0 0 10 . 1 10 . 1
0 0 10 . 1 10 . 2
B
6 6
6 6
. (1.73)

Calculados os auto-valores (ver comentrios sobre a Eq. (1.59)), os resultados so:
(-0,106 i 61,8) e (-1,895 i 161,8). So valores iguais aos encontrados na Seo 1.4.
Os auto-vetores, que agora so vetores coluna com quatro posies, so obtidos com o
auxlio da Eq. (1.59). Os primeiros elementos de cada auto-vetor foram admitidos com
valores unitrios, e o resultado est mostrado abaixo, correspondendo respectivamente
aos auto-valores relacionados acima. Os auto-vetores esto reunidos como colunas da
19

matriz []. Pode-se perceber que as metades superiores das colunas correspondem aos
auto-vetores j encontrados na Seo 1.4, sendo que as partes inferiores so iguais s
superiores multiplicadas pelos correspondentes auto-valores (lembrar de {y} = {x | x }
T
).

| |
(
(
(
(

+ +
+ +
+ +
= O
0 , 100 i 618 , 2 0 , 100 i 618 , 2 0 , 100 i 382 , 0 0 , 100 i 382 , 0
8 , 161 i 895 , 1 8 , 161 i 895 , 1 8 , 61 i 106 , 0 8 , 61 i 106 , 0
009 , 0 i 618 , 0 009 , 0 i 618 , 0 009 , 0 i 618 , 1 009 , 0 i 618 , 1
000 , 1 000 , 1 000 , 1 000 , 1
. (1.74)

Como condio inicial admite-se que tenham sido aplicadas foras estticas
provocando deslocamentos nas massas m
1
e m
2
respectivamente iguais a 0,2 e 0,1 m. O
sistema ser solto a partir desta posio deformada, portanto sem velocidades iniciais.
Logo o vetor de condies iniciais resulta: {y(0)} = { x
0
| v
0
}
T
= { 0,2 0,1 0,00 0,00 }
T
.
Aplicando-se ento a Eq. (1.72) possvel calcular o vetor que rene os
deslocamentos e velocidades como funes do tempo, {y(t)}. Na Fig. 1.10 esto
mostradas as respostas temporais do sistema, que compem o vetor {y(t)} = {x
1
(t) x
2
(t)
) t ( x ) t ( x
2 1
}
T
.



Figura 1.10: Respostas do sistema em termos de deslocamentos (x
1
(t) e x
2
(t) - duas
curvas superiores) e em termos de velocidades ( ) t ( x e ) t ( x
2 1
- duas curvas inferiores).

20

1.7 Sistemas com amortecimento no proporcional resposta forada

O sistema que ser analisado semelhante ao da Seo 1.6, porm com a aplicao de
foras externas. Assim a Eq. (1.53) deve ser rescrita na forma:

} f { } x { ] K [ } x { ] C [ } x { ] M [ = + + . (1.75)

A equao acima, mais a Eq. (1.56), permitem montar a equao matricial:

} g {
0
f
} y {
M 0
0 K
} y {
0 M
M C
=
)
`

=
(

+
(

, (1.76)
ou simplesmente:

} g { } y { ] B [ } y { ] A [ = + . (1.77)

O desenvolvimento abaixo segue nos mesmos moldes daquele aplicado na Seo 1.5,
procurando-se desenvolver relaes em termos de frequncia. Inicialmente admite-se que todas
as foras aplicada possuem a mesma e nica frequncia , ou seja, tem-se o vetor de foras
externas {g} = {G} e
it
. Em consequncia, como o sistema linear, as respostas tambm
possuem o mesmo comportamento: {y} = {Y} e
it
. Aplicando estas expresses na Eq. (1.77) se
obtm:
i [A] {Y} + [B] {Y} = {G} . (1.78)

Realiza-se agora a mudana de coordenadas:

{Y} = [] {P} , (1.79)

onde [] a matriz de auto-vetores complexos (ver Seo anterior).
Substituindo a Eq. (1.79) na Eq. (1.78) se obtm:

i [A] [] {P} + [B] [] {P} = {G} , (1.80)

a qual, pr-multiplicada por [
*
]
T
, fornece:

i [
*
]
T
[A] [] {P} + [
*
]
T
[B] [] {P} = [
*
]
T
{G} = {F
g
} , (1.81)

onde {F
g
} o vetor de foras generalizadas.
As multiplicaes de matrizes efetuadas na Eq. (1.81) diagonalizam as matrizes [A] e [B],
fornecendo [diag{a
i
}] e [diag{b
i
}]. Portanto cada uma das linhas desta equao fica na forma:

( )
i
g i i i
F P b a i = + e , (1.82)

ou, explicitando P
i
:

i i
g
i i
g
i i
i
F
) s i ( a
1
F
b a i
1
P
e
=
+ e
= , (1.83)

onde s
i
o correspondente auto-valor complexo.
Variando-se o ndice i na Eq. (1.83), de 1 a 2n, obtm-se um conjunto de equaes que
pode ser escrito na seguinte forma matricial:

} F {
) s i ( a
1
diag } P {
g
i i
(

)
`

e
= . (1.84)

21

Levando em conta as Eqs. (1.79) e (1.81), se obtm:

| | | | } G {
) s i ( a
1
diag } Y {
T *
i i
O
(

)
`

e
O = . (1.85)
Admitindo {f} = {F} e
it
, finalmente tem-se a equao para {Y}= {X | X

}
T
:

| | | |
)
`

O
(

)
`

e
O =
)
`

0
F
) s i ( a
1
diag
X
X
T *
i i

. (1.86)

interessante verificar a semelhana entre a Eq. (1.86) e a Eq. (1.52).

Exemplo:

a) Seja o mesmo sistema com amortecimento no proporcional do exemplo da seo
anterior, Seo 1.6. Os auto-valores s
i
, como se viu, adotaram os valores (-0,106
i 61,8) e (-1,895 i 161,8). A diagonalizao das matrizes [A] e [B] pode ser obtida
com o auxlio da matriz [] l definida (ver Eq. (1.74)), fornecendo:

[
*
]
T
[A] [] = [diag{ (3,58.10
2
+ i 4,47.10
4
) (3,58.10
2
- i 4,47.10
4
) ...
... (-3,58.10
2
+ i 4,47.10
4
) (-3,58.10
2
- i 4,47.10
4
) }]
e (1.87)
[
*
]
T
[B] [] = [diag{ (2,76.10
6
- i 1,74.10
4
) (2,76.10
6
+ i 1,74.10
4
) ...
... (7,23.10
6
+ i 1,43.10
5
) (7,23.10
6
- i 1,43.10
5
) }] .

Pode-se conferir que as razes entre os valores de b
i
e a
i
fornecem os valores s
i
.
Aplica-se agora apenas uma fora f
1
na massa m
1
, com amplitude F
1
= 10.000N.
Em decorrncia, o vetor simples de foras fica na forma: {F} = {10.000 0}
T
. Pode-se
observar a aplicao da fora na Fig. 1.11.

Figura 1.11: Sistema com dois graus de liberdade
sujeito a uma nica fora externa.

Aplicada a Eq. (1.86), variando-se na faixa de 0 a 250 rad/s, foram obtidos os
vetores complexos {X} e de { X

} como funes de . Na Fig.1.12 esto mostradas as

curvas relativas a |X
1
| e |X
2
|.
Percebe-se nas duas curvas da Fig. 1.12 a ocorrncia de picos de ressonncia
prximos s frequncias naturais amortecidas, que so as partes imaginrias dos auto-
valores: 61,8 e 161,8 rad/s.
Alm disso, quando se analisa a primeira curva (relativa a |X
1
|), percebe-se que
h uma resposta muito baixa em torno de 100 rad/s. Isto acontece porque, neste caso,
a massa m
2
, conectada pela mola de rigidez k
2
e pelo amortecedor de constante c
2
,
funciona como um neutralizador dinmico para o conjunto definido pela massa m
1
e a
mola de rigidez k
1
. A frequncia natural no amortecida, considerando o neutralizador
como um sistema independente, seria igual a 100 100 10 . 1 m k
6
2 2
= = rad/s, que
a frequncia em torno da qual ele apresenta o seu efeito.

22

Figura 1.12: Valores de |X
1
| e |X
2
| como funes de .

Os picos nas curvas da Fig. 1.12 apresentam-se nas mesmas frequncias
naturais. Admitindo que os auto-valores complexos possam ser colocados na forma
i i
n
2
i n i
1 i e , e , , os valores resultantes dos coeficientes de amortecimento
dos modos 1 e 2 seriam respectivamente ,
1
= 0,0017 e ,
2
= 0,0117. Isto explicaria
porque, na Fig. 1.12, os picos correspondentes ao primeiro modo se apresentam bem
mais afiados do que os picos relativos ao segundo modo.





























23

CAPTULO 2: Sistemas contnuos

Os sistemas contnuos, tais como vigas, eixos, colunas, placas, corpos slidos, volumes de
gases, etc ..., so sistemas que requerem um nmero infinito de coordenadas de deslocamento
para que se possam definir exatamente as localizaes de todos os seus pontos. Eles so
abordados, ento, admitindo-se funes contnuas que, por exemplo, no espao tridimensional,
possuem como variveis as coordenadas de localizao fsica de cada ponto, x, y e z. Alm
disso, como se estuda aqui o comportamento dinmico dos mesmos, a varivel temporal t
tambm deve ser considerada. Se u, por exemplo, o deslocamento de cada ponto de um corpo
na direo x, ir surgir uma funo u(x,y,z,t). As derivadas espaciais e temporais envolvidas
passam ento, obviamente, a se apresentar na forma de derivadas parciais.
Nestes estudos de dinmica aparece naturalmente a equao da onda para ser resolvida, ou
em alguns casos uma equao semelhante, cuja soluo segue os mesmos caminhos [2,5,6,7,8].
Na soluo da equao da onda surgem novamente problemas de auto-valores e auto-
vetores, a partir de situaes de movimento livre, que permitem determinar frequncias naturais
de vibrao e correspondentes formas de vibrao (agora como funes espaciais contnuas).
Sero analisados tambm problemas de valores iniciais, quando o corpo sujeito a
condies iniciais de deslocamento e de velocidade e a seguir liberado para apresentar as
consequentes oscilaes livres.
Finalmente analisam-se as situaes de vibraes foradas, quando os sistemas esto
sujeitos a oscilaes induzidas por agentes externos.

2.1 Equao da onda: formulao geral e casos particulares

A equao da onda, no espao tridimensional, aplicada funo u(x,y,z,t), dada por:

0 a ,
t
u
a
1
z
u
y
u
x
u
2
2
2 2
2
2
2
2
2
>
c
c
=
c
c
+
c
c
+
c
c
. (2.1)

Sero aqui analisados problemas unidimensionais, isto , de propagao em uma nica
direo em vigas ou dutos de ar retilneos. Portanto tem-se, neste caso, a verso simplificada da
Eq. (2.1), para a funo u(x,t) de apenas duas variveis:

2
2
2 2
2
t
u
a
1
x
u
c
c
=
c
c
. (2.2)

Analisando a Eq. (2.2) verifica-se que, em virtude da derivada dupla em relao varivel
espacial x, so necessrias duas condies de contorno, normalmente tomando-se uma em cada
extremo (x = 0 e x = L) da regio analisada. A derivada temporal dupla exige o fornecimento de
duas condies iniciais, uma em termos da funo original e outra em funo da sua derivada
temporal (deslocamento e velocidade, por exemplo).
Os desenvolvimentos das vrias formas da equao da onda unidimensional (abrangendo o
estudo de vibraes de vigas retilneas sob carga axial, toro ou flexo e de cabo flexvel sob
tenso, como tambm de propagao sonora em duto retilneo), bem como as condies de
contorno pertinentes, esto apresentados no Apndice A desta apostila.

2.2 Vibraes livres problemas de auto-valores

Na soluo de um problema de valores no contorno, o primeiro passo consiste, de forma
geral, em aplicar as condies de contorno espaciais. Deste procedimento resulta um problema
de auto-valores, cuja soluo em primeira instncia (os prprios auto-valores) esto
24

relacionados s frequncias naturais presentes no sistema e, como segundo conjunto de
informaes, as formas de vibrao (ou oscilao) correspondentes, os auto-vetores. A tcnica
utilizada a de separao de variveis, em que por exemplo a funo u(x,t) subdividida em
uma funo X(x) s da varivel x e outra T(t) s de t, na forma de um produto: u(x,t) = X(x) T(t).

Exemplo:

a) Seja uma viga com propriedades constantes, com uma extremidade fixa e outra livre,
conforme a Fig. 2.1, sob movimentos de toro.
Tem-se, inicialmente, neste caso, a equao diferencial parcial (Eq. (A.27) do
Apndice A):


2
2
2 2
2
t
) t , x (
a
1
x
) t , x (
c
u c
=
c
u c
, (2.3)

com as condies de contorno espaciais:

u(0,t) = 0
e (2.4)
T(L,t) = G J u
x
(L,t) = 0 .


Figura 2.1: Exemplo de viga com extremidades fixa e livre.

Aplica-se separao de variveis com u(x,t) = X(x) T(t), e a equao da onda
resulta assim:
' ' T X
a
1
T ' ' X
2
= , (2.5)
ou
= =
T
' ' T
a
1
X
' ' X
2
. (2.6)

Nesta ltima equao chega-se concluso de que existe uma funo s da
varivel x que igual a uma funo s da varivel t. Em consequncia, elas s podem
ser iguais a uma constante, identificada como .
Usando a mesma separao de variveis, as condies de contorno acima
fornecem:

u(0,t) = X(0) T(t) = 0 ou X(0) = 0 (2.7)
e
u
x
(L,t) = X(L) T(t) = 0 ou X(L) = 0 . (2.8)

25

Analisando o problema em X(x), tem-se a equao diferencial ordinria:

X(x) - X(x) = 0 , (2.9)

mais as condies de contorno (Eqs. (2.7) e (2.8)) acima apresentadas, em x = 0 e
x = L.
A equao auxiliar para encontrar as solues da equao diferencial (2.9) :

m
2
- = 0 , (2.10)

cujas razes so m
1
e m
2
. Consequentemente, para m
1
= m
2
, as solues da Eq. (2.9)
so
x m
1
e e
x m
2
e . Para m
1
= m
2
= m, as solues so e
mx
e x e
mx
.
Para = 0, a Eq. (2.9) se reduz a:

X(x) = 0 , (2.11)
cuja soluo :

X(x) = C
1
+ C
2
x . (2.12)

Observao: a Eq. (2.12) tambm pode ser obtida com o auxlio da Eq. (2.10), que
fornece , ento, m
1
= m
2
= 0, quando e
mx
= e
0x
= 1.
Aplicando a condio (2.7) Eq. (2.12) obtm-se:

X(0) = C
1
+ C
2
0 = 0 , (2.13)

o que fornece C
1
= 0. Derivando a Eq. (2.12), obtida a equao:

X(x) = C
2
. (2.14)

Levando agora a condio (2.8) Eq. (2.14), chega-se a:

X(L) = C
2
= 0 , (2.15)

cuja concluso C
2
= 0. Assim, voltando Eq. (2.12), para = 0 resulta apenas a
soluo trivial (e indesejada) X(x) = 0.
Para > 0, a Eq. (2.9) fornece as razes distintas e - . Em consequncia, a
soluo neste caso fica na forma:


x
2
x
1
e C e C ) x ( X

+ = . (2.16)

Aplicando-se a primeira equao de contorno, Eq. (2.7), obtm-se o resultado:

X(0) = C
1
+ C
2
= 0 . (2.17)

A derivao da Eq. (2.16) fornece:


x
2
x
1
e C e C ) x ( ' X

= (2.18)

Aplicando a segunda condio de contorno, Eq. (2.8), Eq. (2.18), obtm-se:

0 e C e C ) L ( ' X
L
2
L
1
= =

(2.19)

As Eqs. (2.17) e (2.19) formam um sistema homogneo de equaes lineares em
C
1
e C
2
. Como estas duas equaes no so redundantes, a nica soluo possvel
C
1
= C
2
= 0 que, levada Eq. (2.16), fornece novamente a soluo trivial X(x) = 0.
26

Finalmente, deve-se testar a possibilidade de haver soluo no nula para < 0.
Para tais valores de a Eq. (2.10) fornece as razes i e - i e, por
consequncia, a soluo adota a forma:


x i
2
x i
1
e C e C ) x ( X

+ = . (2.20)

Lembrando da equao de Euler (e
iu
= cos u + i sen u), obtm-se assim a
proposta de soluo modificada:

) x cos( C ) x sen( C ) x ( X
2 1
+ = . (2.21)

Aplicando a primeira condio de contorno, Eq. (2.7):

X(0) = 0 => C
2
= 0 . (2.22)

Sobra portanto
) x sen( C ) x ( X
1
= , (2.23)
com derivada
) x cos( C ) x ( ' X
1
= . (2.24)

Aplicando agora a segunda condio de contorno, Eq. (2.8), obtm-se:

0 ) L cos( = , (2.25)
condio que obtida quando:


2
) 1 n 2 ( L
n
t
+ = , n = 0, 1, 2, ... (2.26)
ou

2
2 2
n
L 4
) 1 n 2 ( t +
= , n = 0, 1, 2, ... . (2.27)

Retornando equao de X(x), so obtidas as autofunes:


(

t +
=
L 2
x ) 1 n 2 (
sen ) x ( X
n
, n = 0, 1, 2, ... . (2.28)

Na busca da soluo T(t) deve-se extrair a equao T - a
2
T = 0 da parte
final da equao (2.6), sendo que, substituindo-se o valor de , tem-se:

0 ) t ( T
L 4
a ) 1 n 2 (
) t ( ' ' T
2
2 2 2
=
t +
+ , (2.29)
cuja soluo fornece:

(

t +
+
(

t +
=
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D ) t ( T
n 2 n 1 n
. (2.30)

Assim, a auto-funo de x e de t, ligada a cada auto-valor
n
, dada por:


)
`

t +
+
(

t +
(

t +
= u
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D
L 2
x ) 1 n 2 (
sen ) t , x (
n 2 n 1 n
. (2.31)
27

Finalmente tem-se a soluo final admitindo a srie:

=
u = u
0 n
n
) t , x ( ) t , x ( , (2.32)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de
giro e de velocidade angular da viga (condies iniciais).
Do desenvolvimento acima percebe-se que existem vrias formas da viga vibrar
livremente, que so as formas dos modos de vibrao, dadas pelas funes X
n
(x),
apresentadas na Eq. (2.28). A cada uma destas formas existe uma frequncia natural
de vibrao,
n
, que o multiplicador da varivel t nas Eqs. (2.30) e (2.31), ou seja, a
expresso:
... , 2 , 1 , 0 n ,
L 2
a ) 1 n 2 (
n
=
t +
= e . (2.33)

A frequncia dita fundamental a mais baixa do conjunto, portanto dada por

0
= a / (2 L). As harmnicas, como so chamadas, neste caso seriam as mltiplas
mpares da fundamental: 3
0
, 5
0
, 7
0
, ... . Na Fig. 2.2 abaixo so mostradas as
formas de vibrao de alguns modos, indicando-se ainda as frequncias naturais
correspondentes.

Forma de modo 1:
0
. Forma de modo 2: 3
0
.

Forma de modo 3: 5
0
. Forma de modo 4: 7
0
.

Figura 2.2: Quatro primeiros modos de vibrao
da viga sob toro, engastada-livre.

28

Percebe-se claramente, nas curvas da Fig. 2.2, que todas elas obedecem s
condies de contorno espaciais, iniciando no valor zero e terminando com derivada
(inclinao) nula. Alm disso, o nmero de pontos internos de n (amplitude zero) vai
crescendo progressivamente: zero no primeiro modo, um no segundo, dois no terceiro,
etc ... .

2.3 Vibraes livres problemas de valores iniciais

A equao da onda, como j observado acima, possui uma derivada temporal dupla.
Exige, assim, que seja informado o perfil de deslocamentos e o perfil de velocidades no incio de
um problema de valores iniciais.
Se fosse analisado, por exemplo, o caso de vibraes torcionais do exemplo da Seo 2.2,
a primeira condio seria fornecer uma funo f(x) que indica como o sistema se encontra
deformado no tempo inicial, o qual pode-se tomar como sendo t = 0. Assim, neste caso, a
Eq. (2.31) fornece:
(

t +
= u
L 2
x ) 1 n 2 (
sen D ) 0 , x (
n 1 n
, (2.34)

e a Eq. (2.32), por sua vez, fica na forma:

) x ( f
L 2
x ) 1 n 2 (
sen D ) 0 , x (
0 n
n 1
=
(

t +
= u

=
. (2.35)

Na Eq. (2.35) fica evidente que as constantes D
1n
nada mais so que os coeficientes de
Fourier da funo f(x) quando ela expandida em uma srie de funes de x, que so os senos
que aparecem nas Eqs. (2.34) e (2.35).
A expresso de
n
(x,t), Eq. (2.31), quando derivada em relao ao tempo, fornece:


L 2
a ) 1 n 2 (
L 2
x ) 1 n 2 (
sen ) t , x (
t
n
t +
(

t +
= u
c
c


)
`

t +
+
(

t +

L 2
t a ) 1 n 2 (
cos D
L 2
t a ) 1 n 2 (
sen D
n 2 n 1
, (2.36)
a qual, para t = 0 se resume a:


(

t + t +
= u
c
c
L 2
x ) 1 n 2 (
sen
L 2
a ) 1 n 2 (
D ) 0 , x (
t
n 2 n
. (2.37)

Assim, no caso de derivada temporal, considerando que seja fornecida a funo g(x) como
o perfil de velocidades da viga no incio do movimento, tem-se que a derivada da Eq. (2.32)
fornece, para t = 0:

) x ( g
L 2
x ) 1 n 2 (
sen
L 2
a ) 1 n 2 (
D ) 0 , x (
t
0 n
n 2
=
(

t + t +
= u
c
c

=
. (2.38)

A concluso, semelhante obtida para a Eq. (2.35), a de que os valores
D
2n
(2n+1) a /(2 L) nada mais so do que os coeficientes de Fourier da funo g(x) com relao
s funes de x (senos) que aparecem na Eq. (2.38).
Os valores de D
1n
e D
2n
podem ser portanto determinados com o auxlio das Eqs. (2.35) e
(2.38), e a soluo do problema de valores iniciais dada pela Eq. (2.32).
29

Exemplo:

a) Seja a mesma viga do exemplo da seo anterior, com propriedades constantes, com
uma extremidade fixa e outra livre, sob movimentos de toro.
Admite-se que, como condio inicial, que a viga seja sujeita a um torque
positivo T
e
na metade de seu comprimento, ou seja, para x = L/2.

Figura 2.3: Aplicao do momento T
e
.

O ngulo de toro para um eixo de seo e torque aplicado constantes,
conforme a mecnica dos slidos, dado pelo produto do torque pelo comprimento
dividido pelo produto JG. Assim, no caso presente, a deformao total verificada na
primeira metade do eixo dada por:


G J 2
L T
G J
) 2 / L ( T
e e
T
= = u . (2.39)

Na primeira metade o ngulo varia linearmente do valor zero ao valor
T
e na
segunda metade o ngulo permanece constante, igual a
T
, conforme a Fig. 2.4.


Figura 2.4: Distribuio inicial de ngulos.

Com base na Fig. 2.4, as equaes que definem a funo (x,0) = f(x) so dadas
por:

s s
s s
=
. L x 2 / L ,
G J 2
L T
, 2 / L x 0 ,
G J
x T
) x ( f
e
e
(2.40)

30

Uma vez que o eixo esteja deformado, ele ser solto desta posio esttica.
Consequentemente, o perfil de velocidades iniciais nulo, ou seja,
/ t (x,0) = g(x) = 0. Assim sendo, devero ser calculados os valores D
1n
(ver
Eq. (2.35)), mas os valores de D
2n
so todos nulos (ver Eq. (2.38)).
Os valores de D
1n
so obtidos com base no clculo de coeficientes de Fourier,
fornecendo:

=
(

t +

=
}
L
0
n 1
dx
L 2
x ) 1 n 2 (
sen ) x ( f
0 L
2
D

=
(

t +
+
(

t +
=
} }
L
2 / L
e
2 / L
0
e
dx
L 2
x ) 1 n 2 (
sen
G J 2
L T
L
2
dx
L 2
x ) 1 n 2 (
sen
G J
x T
L
2



(

t +
t +
=
4
) 1 n 2 (
sen
G J ) 1 n 2 (
L T 8
2 2
e
. (2.41)

Como neste caso s existem os D
1n
, pois as velocidades iniciais so nulas, a
auto-funo relativa a
n
seria obtida levando-se os valores obtidos atravs da
Eq. (2.41) na equao abaixo, que uma particularizao da Eq. (2.31):


(

t +
(

t +
= u
L 2
t a ) 1 n 2 (
cos
L 2
x ) 1 n 2 (
sen D ) t , x (
n 1 n
, (2.42)

sendo que a soluo final, portanto, seria:

=
u = u
0 n
n
) t , x ( ) t , x ( . (2.43)

2.4 Vibraes foradas

Na apresentao deste estudo torna-se necessria a escolha de uma situao prtica, para
melhor apresentar os clculos envolvidos. Foi escolhido o caso de uma viga sob flexo, bi-
articulada (este exemplo est desenvolvido no Apndice A, ao final desta apostila), conforme a
Fig. 2.5.

Figura 2.5: Viga bi-articulada, sob flexo.

No caso da flexo tem-se:


2
2
2
2
2
2
t
) t , x ( v
) x ( m
x
) t , x ( v
) x ( EI
x c
c
=
(

c
c
c
c
. (2.44)
31

No caso de EI e m constantes, a Eq. (2.44) se simplifica para:


2
2
4
4
t
) t , x ( v
m
x
) t , x ( v
EI
c
c
=
c
c
. (2.45)
Admitindo-se a viga bi-articulada (ou seja, com deslocamento v e momento EI v
xx
nulos
em ambas as extremidades), as frequncias naturais no amortecidas so dadas por:


2
2 2 2
n
L
a n t
= e , n = 1, 2, 3, ... (2.46)

onde a
4
= E I / m. As correspondentes auto-funes (as formas de vibrao) so dadas por:


|
.
|

\
|
t
=
L
x n
sen
mL
2
) x ( X
n
, n = 1, 2, 3, ... (2.47)

As funes que aparecem na Eq. (2.47) foram normalizadas de tal forma que so
obedecidas as relaes de ortogonalidade:

}
o =
L
0
rs s r
dx ) x ( X ) x ( X m , r,s = 1, 2, 3, ... (2.48)
e

}
o e =
L
0
rs
2
r
4
s
4
r
dx
dx
) x ( X d
) x ( X EI , r,s = 1, 2, 3, ... , (2.49)

onde
rs
o conhecido delta de Kronecker, que vale a unidade quando r = s e nulo quando r s.
Quando a vibrao forada, atravs da aplicao de foras transversais segundo a funo
f(x,t), a Eq. (2.45) se transforma em:


2
2
4
4
t
) t , x ( v
m ) t , x ( f
x
) t , x ( v
EI
c
c
= +
c
c
. (2.50)

A soluo v(x,t) pode ser obtida por superposio modal:

=
=
1 r
r r
) t ( q ) x ( X ) t , x ( v . (2.51)

Substituindo a Eq. (2.51) na Eq. (2.50) se obtm:

=
= +
1 r 1 r
4
r
4
r r r
) t , x ( f
dx
) x ( X d
EI ) t ( q ) x ( X m ) t ( q . (2.52)

Multiplicando a equao acima por X
s
(x) e integrando de 0 a L, lembrando ainda das
Eqs. (2.48) e (2.49), obtm-se um conjunto de equaes diferenciais ordinrias independentes, na
forma:
) t ( f ) t ( q ) t ( q
r
q r
2
r r
= e + , r = 1, 2, 3, ... , (2.53)
onde

}
=
L
0
r
r
q
dx ) x ( X ) t , x ( f ) t ( f , r = 1, 2, 3, ... , (2.54)

so as foras generalizadas associadas s coordenadas generalizadas q
r
(t).
32

Cada uma das Eqs. (2.53) equivalente equao da dinmica de um sistema massa-mola
sob a ao de uma fora externa f(t):

) t ( f ) t ( x k ) t ( x m = + , (2.55)
que, dividida por m, fornece:

) t ( f ) m / 1 ( ) t ( x ) t ( x
2
n
= e + . (2.56)

Entretanto, como se pode perceber na Eq. (2.53), a formulao do problema no prev um
termo de amortecimento. Portanto, se fosse procurada uma resposta forada em frequncia,
como se realizou no captulo anterior, a curva em frequncia resultante apresentaria picos de
ressonncia com amplitudes infinitas nas frequncias naturais do sistema. Em virtude deste fato
no se procurar desenvolver aqui uma expresso final para tal funo resposta em frequncia.
O importante perceber que, de forma semelhante ao que se viu no Captulo 1, cada
coordenada generalizada (neste caso em que no h amortecimento) possui um comportamento
independente, fornecendo na sua prpria funo resposta em frequncia um pico de amplitude
infinita na correspondente frequncia natural. E a resposta final do sistema, obtida atravs da
Eq. (2.51), seria uma combinao das formas de vibrao dos vrios modos multiplicadas pelas
suas coordenadas generalizadas. Assim, na funo resposta em frequncia de todo o sistema,
haveria infinitos picos de amplitudes infinitas, um em cada frequncia natural do sistema.
A adoo de um mecanismo de amortecimento viria, obviamente, a tornar finitas as
amplitudes de todos os picos de ressonncia. Assim, a adoo de mais um termo na Eq. (2.50),
correspondente ao amortecimento, ou mesmo a considerao, nesta equao, de um valor
complexo para o mdulo de elasticidade E (neste caso estar-se-ia optando pelo modelo de
amortecimento conhecido como estrutural ou histertico), tornaria a sua resposta mais
adequada realidade.

2.5 Energias cintica e potencial

Seja uma viga sob cargas axiais. Pode-se isolar um elemento de comprimento infinitesimal
da mesma, conforme a Fig. 2.6.

Figura 2.6: Elemento de viga sob cargas axiais N(x).

Lembrando que a energia cintica de uma massa M sob velocidade v dada por (1/2)M v
2
,
a energia cintica deste pequeno elemento seria dada por:


2
t
) t , x ( u
] dx ) x ( m [
2
1
dT
(

c
c
= , (2.57)

onde m(x) a massa da viga por unidade de comprimento.
33

Portanto a energia cintica total da viga de comprimento L seria dada por:


}
(

c
c
=
L
0
2
dx
t
) t , x ( u
) x ( m
2
1
T . (2.58)

O clculo da energia potencial relacionada ao elemento da Fig. 2.6 de compreenso mais
fcil quando se faz uma analogia com uma mola. Para uma mola (que apresenta comportamento
linear) com constante de rigidez k, a relao entra fora aplicada F e a sua deflexo u dada por
F = k u. A energia potencial de uma mola (trabalho realizado sobre a mesma durante a
deformao) ento dada por:

x ) x k (
2
1
x k
2
1
du u k du F V
2
x
0
x
0
A A = A = = =
} }
A A
. (2.59)

Percebe-se ento que a energia potencial igual metade do produto da fora final (k x)
pela deformao final (x). No caso do elemento mostrado na Fig. 2.6, a fora aplicada,
segundo a mecnica dos slidos, dada por:


x
) t , x ( u
) x ( EA ) t , x ( E ) x ( A ) t , x ( ) x ( A ) t , x ( N
c
c
= c = o = . (2.60)

A deformao total do elemento, tambm pela mecnica dos slidos, dada por:

dx
x
) t , x ( u
dx ) t , x ( ) t , x ( x
c
c
= c = A . (2.61)

Assim sendo, a energia potencial armazenada no elemento de comprimento dx calculada
atravs de:

dx
x
) t , x ( u
) x ( EA
2
1
dx
x
) t , x ( u
x
) t , x ( u
) x ( EA
2
1
dV
2
(

c
c
=
(

c
c
(

c
c
= , (2.62)

e a energia calculada para toda a viga resulta:

dx
x
) t , x ( u
) x ( EA
2
1
V
2
L
0 (

c
c
=
}
. (2.63)

O desenvolvimento acima foi obtido analisando-se cargas axiais em vigas. Equaes
semelhantes poderiam ser obtidas para outros tipos de carregamento, como a toro e a flexo.
Como exemplo, no caso da flexo as energias cintica e potencial [2] so dadas
respectivamente por:

} (

c
c
=
L
0
2
dx
t
) t , x ( v
) x ( m
2
1
T (2.64)
e
dx
x
) t , x ( v
) x ( EI
2
1
V
2
2
2
L
0
(

c
c
=
}
, (2.65)

onde v(x,t) , neste caso, o deslocamento transversal (ou lateral) da viga, sendo m(x) e EI(x)
respectivamente as distribuies dos parmetros m (a massa por unidade de comprimento) e EI
(o mdulo de elasticidade vezes o momento de inrcia da seo) ao longo da viga.
34

2.6 Concluso

Neste captulo foi possvel estudar o comportamento vibratrio de sistemas contnuos,
porm em casos bastante simples.
Assim, os sistemas analisados foram do tipo unidimensional, o que equivale a dizer que, do
ponto de vista espacial, apenas uma varivel (x) esteve envolvida. Alm disso, as vigas e o duto
considerados tiveram suas geometrias mantidas constantes ao longo desta varivel espacial. Para
finalizar, condies de contorno bastante simples foram impostas durante a soluo dos
problemas.
Do ponto de vista prtico, estas condies so absurdamente restritivas. Dificilmente se
encontraria um elemento estrutural que pudesse ser analisado da forma como foram resolvidos os
exemplos aqui apresentados (e tambm no Apndice A). Entretanto, o estudo desenvolvido
neste Captulo 2 permite entender que os sistemas contnuos possuem infinitas frequncias
naturais, sendo que a cada uma delas est associada uma forma espacial de vibrar (envolvendo
perfis de deformao contnuos, ao longo de todo o elemento).
A anlise de peas de geometria mais complexa possvel atravs, por exemplo, do
Mtodo dos Elementos Finitos (ou do Mtodo dos Elementos de Contorno). Nestes casos a pea
subdividida (ou apenas o seu contorno) em inmeros elementos de pequenas dimenses.
Tais elementos, geralmente de forma simples (poliedros), so localizados e definidos
atravs de pontos extremos, denominados ns. Para anlise de vibraes, por exemplo, cada n
pode apresentar trs movimentos de translao (x, y e z) e trs de rotao (u
x
, u
y
e u
z
), o que
implica, no caso geral, em seis graus de liberdade por n. Como o problema vai ser discretizado
por vrios elementos com vrios ns, o nmero n de graus de liberdade resulta bastante elevado,
sendo comum a anlise de problemas com at alguns milhes de variveis.
Em todos estes elementos as equaes diferenciais so resolvidas de forma aproximada,
resultando em um sistema linear de equaes, onde os graus de liberdade (ou coordenadas
generalizadas) so as incgnitas do problema. Isto permite a montagem de um sistema local de
equaes para cada elemento. Reunindo todas as equaes, obtido um sistema com n
equaes, a partir do qual podem ser extradas as matrizes de massa e de rigidez (de dimenses
nxn) referentes pea sob estudo. Com base nas matrizes de massa e de rigidez, a exemplo do
que foi feito no Captulo 1, podem ser calculadas as frequncias naturais no amortecidas e as
formas modais de vibrao da pea.
Normalmente so empregados mtodos numricos que calculam apenas algumas
frequncias naturais, pois o clculo de todas elas se torna uma tarefa computacional muito
pesada. As frequncias mais importantes, em geral, so as mais baixas, pois so estes modos de
baixas frequncias que aparecem com maior intensidade nas respostas dos sistemas. Se,
eventualmente, fosse possvel calcular todas as frequncias naturais, atravs do Mtodo dos
Elementos Finitos, somente a primeira metade delas apresentaria valores prximos aos reais. O
processo de diviso do sistema contnuo em pequenos elementos consiste numa aproximao e,
portanto, h um preo a pagar. Os desvios maiores acontecem em altas frequncias, pois nesta
faixa que as formas de vibrao so mais complexas, e a discretizao adotada no consegue
representar as variaes mais abruptas que ento ocorrem.









35

CAPTULO 3: Anlise modal experimental

O objetivo deste captulo fornecer informaes bsicas sobre alguns mtodos que
permitem obter os parmetros modais da estrutura, que normalmente so a frequncia natural,
o fator de amortecimento e a forma modal para cada um dos modos identificados. So aqui
analisados apenas mtodos no domnio da frequncia, que usam como dados de entrada as
funes resposta em frequncia (FRFs), identificadas posteriormente. H, tambm, mtodos
no domnio do tempo, que so aplicados sobre respostas temporais livres da estrutura [11,12].
Estes, entretanto, no so discutidos nesta obra.
Neste captulo so fornecidas, na Seo 3.1, informaes sobre as formas de fixar as peas
que sero submetidas anlise modal experimental. So discutidas as vantagens e desvantagens
de cada uma delas e as suas influncias nos resultados obtidos dos testes experimentais.
Na Seo 3.2 so apresentadas as vrias maneiras pelas quais possvel aplicar foras ao
objeto sob teste, no intuito de faz-lo vibrar, ao passo que na Seo 3.3 so discutidas as formas
de aplicar vibradores ao objeto de teste (quando necessrio). As respostas foradas (FRFs) so
os dados mais comumente utilizados na identificao experimental dos modos de vibrao.
Tem-se, na Seo 3.4, a interpretao da FRF de um sistema de um grau de liberdade sob
vrias ticas (representaes) distintas. Na Seo 3.5 apresentado rapidamente o embasamento
terico que permite compreender as respostas dos sistemas mecnicos (FRFs) como
composies das respostas dos vrios modos que os compem. Em seguida, na Seo 3.6, so
apresentados alguns mtodos que permitem identificar os parmetros modais a partir das
respostas foradas dos sistemas, obtidas experimentalmente.
Finalmente a Seo 3.7 apresenta os termos residuais de alta e baixa frequncias, que
permitem um melhor ajuste das curvas sintetizadas s curvas experimentais, nestas faixas
extremas de frequncias.
3.1 Fixao da pea a analisar

Sero aqui expostas as maneiras de fixar os objetos que sero submetidos anlise modal,
com os respectivos cuidados que devem ser tomados para a melhor realizao do teste.
H duas condies bsicas para a fixao de uma estrutura: livre ou fixa. Elas so
discutidas a seguir.

3.1.1 Estrutura livre:

A condio perfeitamente livre no possvel de se obter; seria o equivalente a soltar a
estrutura no espao sideral, completamente sem vnculos.
Assim, o que se faz promover a suspenso da estrutura com elementos bastante flexveis,
de forma que a frequncia natural de montagem seja bastante baixa, bem abaixo das frequncias
naturais de deformao da prpria estrutura. A estrutura, ao vibrar na frequncia natural da
suspenso, no se deforma, apenas se move como um corpo rgido.
Uma primeira soluo colocar a estrutura, que normalmente neste caso de pequeno
porte, sobre uma camada de espuma bem flexvel. A realizao do teste em geral se d pela
fixao de um acelermetro em um ponto fixo da estrutura e a aplicao de impactos atravs do
martelo instrumentado ao longo da mesma. O problema principal deste tipo de suspenso que,
pelo fato de a estrutura estar sempre em contato com a espuma, o amortecimento medido
apresenta valores superiores aos reais (a espuma amortece as vibraes).
A segunda soluo suspender a estrutura atravs de fios flexveis, como no modelo
simplificado da Fig. 3.1.
36

A frequncia natural para o movimento transversal direo dos fios (ver setas de
movimentao na Fig. 3.1) dada por:

l
g
2
1
f
n
t
= [Hz] , (3.1)

onde g a acelerao da gravidade e l a distncia do centro de gravidade do corpo aos pontos
superiores de fixao dos fios. Assim, por exemplo, para um valor desta distncia igual a um
metro, a frequncia natural do movimento (balano) transversal de aproximadamente 0,5 Hz.


Figura 3.1: Pndulo simples.

Deve ficar bem claro que a frequncia natural baixa a de balano lateral. Se, por
exemplo, o corpo da Fig. 3.1 for puxado para baixo, a frequncia natural da vibrao vertical
(que impe mudanas de comprimento aos fios) ser bem mais elevada. Assim, a vibrao a ser
aplicada estrutura suspensa deve ser na direo horizontal (transversal ao fio), para aproveitar a
frequncia natural baixa da suspenso nesta direo.
Do ponto de vista prtico, os fios flexveis mais utilizados para estruturas leves so os de
nylon e outro fino, de ao tranado, ambos encontrados como suprimentos em lojas de pesca.
Com a estrutura suspensa por fios pode-se usar um acelermetro fixo e vrias posies de
impacto do martelo instrumentado, ou acoplar um vibrador num certo ponto e fazer uma
varredura espacial com o acelermetro.

3.1.2 Estrutura fixa:

Neste caso, pontos ou regies da pea so conectados rigidamente a pontos externos fixos,
ou seja, tm seus movimentos impedidos.
Embora possa parecer o contrrio, impedir o movimento da estrutura em uma certa regio
pode ser uma tarefa mais difcil do que simular a condio livre. Existe uma razo fundamental
para tal: nenhum ponto de apoio possui uma rigidez infinita, que permita bloquear por completo
os movimentos da estrutura no ponto de fixao.
37

Entretanto, muitos casos prticos exigem que a estrutura seja testada desta forma, qual seja,
engastada. Em muitas situaes, tambm, o objeto de teste deve ser avaliado nas condies de
uso (in situ), como por exemplo uma p de uma turbina (fixa pela base), um motor de
combusto (suspenso por coxins), etc ...
Do ponto de vista do processamento posterior, o teste com a estrutura engastada menos
proveitoso. Quando se testa uma estrutura livre, todos o seus pontos apresentam movimentos.
Atravs de processamento, pode-se posteriormente travar alguns pontos da estrutura,
simulando uma fixao. O contrrio no possvel, ou seja, se a estrutura testada na condio
engastada, no possvel depois simular movimentos para os pontos fixos.

3.2 Aplicando foras estrutura

A anlise modal, no domnio da frequncia, se baseia em funes resposta em frequncia
(FRFs), que so calculadas a partir dos sinais correspondentes fora aplicada estrutura e
resposta da mesma. So discutidas a seguir as maneiras pelas quais as foras podem ser
aplicadas estrutura sob teste. Atualmente, pela facilidade de serem processados os sinais com o
auxlio de analisadores digitais, procura-se excitar a estrutura com uma fora que tenha um
espectro em frequncia amplo, cobrindo toda a faixa de frequncias de interesse. Desta forma,
obtm-se toda a FRF em um nico processamento. Alm disso, esperado que o espectro, na
faixa til, tenha uma amplitude aproximadamente constante, para que a excitao no se
concentre em apenas algumas frequncias da faixa de interesse.
O impacto atravs do martelo instrumentado (ver Fig. 3.2) o primeiro tipo de excitao a
ser analisado. Diz-se que neste caso a excitao sem contato, pois aps o impacto a estrutura
vibra livremente, sem qualquer dispositivo acoplado.

Figura 3.2: Martelo de impacto.

A magnitude do impacto determinada pela massa da cabea do martelo e pela sua
velocidade quando ele colide com a estrutura (quantidade de movimento). A pessoa que
manuseia o martelo costuma manter uma velocidade de impacto mais ou menos constante; logo,
para modificar o nvel da fora, deve-se alterar o valor da massa adicional (ver Fig. 3.2).
A faixa de frequncias determinada pela rigidez da ponteira (uma vez que a massa da
cabea do martelo esteja fixa). Quanto mais rgida a ponteira, menor o tempo de contato T
c

(ver Fig 3.3, curva a)). A frequncia mxima f
c
da regio aproximadamente plana do espectro
correspondente (ver Fig 3.3, curva b)) inversamente proporcional a T
c
, logo para uma ponteira
rgida consegue-se alcanar frequncias mais altas. A ponteira deve ser escolhida de forma que a
regio plana do espectro cubra com pequena folga a faixa de frequncias de interesse; no se
deve desperdiar energia em altas frequncias se no h interesse nelas.
A Fig. 3.4 mostra comparaes entre curvas reais relativas a impactos com martelo
apresentando ponteiras construdas com vrios tipos de material. Na parte a) tm-se as foras
como funes no tempo, ao passo que em b) so apresentados os respectivos espectros em
frequncia.
38



Figura 3.3: Histria temporal do contato do martelo com
a estrutura e correspondente espectro.

Figura 3.4: Foras aplicadas pelo martelo com diferentes ponteiras;
a) curvas no tempo; b) espectros em frequncia.

Outra maneira bastante comum de fazer vibrar um estrutura lhe aplicar foras atravs de
um vibrador. O tipo mais difundido, atualmente, o eletromagntico, que converte sinais
eltricos amplificados em movimentos mecnicos equivalentes. O seu princpio de
funcionamento semelhante ao de um auto-falante, ou seja, o movimento ocorre em decorrncia
da interao entre um campo magntico fixo (im permanente ou bobina fixa) e um campo
magntico varivel, gerado em uma bobina mvel.
39

Comparando foras teis e frequncias mximas, os vibradores podem apresentar valores
bastante distintos, desde um vibrador pequeno que aplica foras com valor pico de 5 N, na faixa
de frequncias de 0 a 10 kHz, at um vibrador de grande porte, que pode aplicar foras de
200.000 N, de 0 a 3 kHz. A frequncia mxima de uso est relacionada frequncia de
ressonncia do prprio aparelho, que, de uma forma geral, diminui com o aumento do seu
tamanho (e, consequentemente, de sua massa).
A Fig. 3.5 apresenta detalhes da conexo do vibrador estrutura, em situaes
consideradas aceitveis ou no. O sensores que ali se aparecem so: o acelermetro, que permite
obter um sinal proporcional acelerao no ponto de instalao; o transdutor de fora que, como
o prprio nome indica, gera um sinal proporcional fora que passa atravs de si; e, finalmente,
a cabea de impedncia, que combina os transdutores anteriores, fornecendo dois sinais de sada
(acelerao e fora).

a) b) c) d)

Figura 3.5: Vrias conexes entre vibrador e estrutura, com sensores.
Montagens aceitveis: a), b) e c). No satisfatria: d).

Como se pode observar nas vrias montagens que aparecem na Fig. 3.5, utiliza-se um
elemento flexvel entre o vibrador e a estrutura. A conexo flexvel usualmente um arame de
ao (dimetro na faixa de 1,0 a 1,5 mm e comprimento de 30 a 40 mm) que tem como funo
principal aplicar estrutura apenas uma fora axial, visto que nesta direo que a sua rigidez
mais elevada. Impede-se assim que sejam transmitidos momentos fletores de valores
significativos, o que no desejvel. Esta conexo funciona ainda, de certa forma, como um
fusvel mecnico, protegendo a clula de fora.
recomendvel que os dois sensores fiquem aplicados o mais prximo possvel da
estrutura, como nos casos a) e b) da Fig. 3.5. No caso c) da mesma figura o transdutor de fora
est um pouco deslocado, o que no causa grande interferncia, pois a massa do elemento
flexvel normalmente muito baixa. Assim, a correspondente fora de inrcia (massa versus
acelerao) no causa alterao significativa no sinal medido. Finalizando, o caso d) da Fig. 3.5
mostra uma situao insatisfatria. Isto porque as deformaes do elemento flexvel (causadas
pelas foras transmitidas) nem sempre so desprezveis, e portanto o movimento do sensor pode
ser significativamente diferente do movimento da estrutura.
O sinal eltrico, gerado eletronicamente, passa por um amplificador de potncia e
injetado no vibrador. Ele pode ser determinstico e transiente, como no caso do chirp, que
uma senide cuja frequncia varia continuamente entre dois valores (ver Fig. 3.6). O seu
espectro resulta aproximadamente plano entre estas frequncias superior e inferior. A sua
utilizao bastante indicada quando se deseja aplicar potncia estrutura numa faixa de
frequncias bem determinada.
40

Um dos sinais mais difundidos na obteno de FRFs o rudo aleatrio, produzido por
um gerador de sinais apropriado. Ele um sinal contnuo e no determinstico, pois no se pode
prever perfeitamente o seu comportamento. Para geradores de boa qualidade, h a possibilidade
de escolher a faixa de frequncias que este rudo ir possuir, dentro da qual o espectro
aproximadamente plano. Tem-se ento o rudo aleatrio de banda estreita. Esta possibilidade
conveniente, pois assim pode-se introduzir vibrao na estrutura s na faixa de interesse,
evitando de jogar energia em frequncias nas quais no h interesse. Quando se fala em rudo
branco, teoricamente seria o rudo aleatrio com espectro plano envolvendo todas as frequncias,
de zero a infinito. Entretanto, tal rudo teria uma potncia infinita, o que obviamente
impossvel. Se um determinado gerador oferece ento a opo de rudo branco, deve-se
investigar a maior frequncia que tal sinal vai atingir.

Figura 3.6: Chirp aproximadamente de 10 a 40 Hz:
a) no tempo e b) na frequncia (espectro).

A Fig. 3.7 mostra um exemplo de sinal aleatrio, onde a curva a) est no domnio do tempo
e a curva b) no domnio da frequncia (espectro). Na funo temporal h 512 pontos separados
por At = 0,001 s. O espectro foi obtido pelo algoritmo FFT (Fast Fourier Transform),
resultando uma curva complexa, simtrica em relao frequncia nula (f = 0 Hz). A curva b)
da Fig. 3.7 mostra os mdulos dos valores da faixa til do espectro, de 0 a 500 Hz (257 pontos
afastados em 1,953 Hz), em decibis (dB), onde se pode perceber que o espectro se distribui
aproximadamente em torno da linha horizontal correspondente ao valor 15 dB.


Figura 3.7: Sinal aleatrio: a) no tempo e
b) na frequncia (espectro).

Uma alternativa ao sinal aleatrio aquele denominado pseudo-aleatrio. Neste caso
tem-se um amostra de sinal aleatrio de comprimento finito (perodo P), que sucessivamente
repetida (ver Fig. 3.8). Este tipo de sinal permite reduzir um dos problemas que aparecem
41

naturalmente no processamento dos sinais [11,12], denominado vazamento (ou leakage, em
ingls).

Figura 3.8: Exemplo de sinal pseudo-aleatrio.

Existe um novo tipo de sinal determinstico e transiente para a realizao de testes baseado
em MLS (Maximum Length Sequences), que so sequncias geradas a partir do estudo de
nmeros inteiros. Estes sinais tambm se distribuem, em termos de espectro, sobre uma ampla
faixa de frequncias. Eles tm tido uma aplicao muito grande na determinao de respostas
impulsivas de sistemas. Permitem repetio perfeita do sinal, o que auxilia na remoo do rudo.

3.3 Aplicao de vibrador

De acordo com a seo anterior, em muitos testes de anlise modal a fonte de vibrao
um vibrador acoplado estrutura. Na Fig. 3.9 esto mostradas algumas montagens, satisfatrias
ou no, discutidas a seguir.


a) b) c) d)

Figura 3.9: Vibradores aplicados s estruturas.
Montagens aceitveis: a), b) e c). No satisfatria: d).

Na primeira situao, caso a), a estrutura se encontra na condio livre e, portanto, j
est se encontra isolada. Assim, o vibrador pode ficar fixo, pois quaisquer vibraes que ele
transmita ao meio circundante no atingiro a estrutura. O que pode ocorrer a estrutura ser
atingida por vibraes que estejam presente no ponto de fixao do vibrador. S que, como estas
vibraes passam pelo arame que une o vibrador estrutura, elas so medidas e processadas
como se tivessem origem no vibrador, no causando maiores problemas.
No caso b), na mesma figura, tanto a estrutura como o vibrador esto na condio livre.
Novamente a estrutura j est, a princpio, isolada, no apresentando meios de ser atingida por
vibraes indesejadas. As vantagens que se tm, em relao ao caso anterior, so: i) as vibraes
42

que atingem a estrutura so somente aquelas geradas no vibrador; ii) o vibrador no provoca
vibraes no meio circundante. Pode ser necessrio adicionar massa ao vibrador para aumentar a
sua inrcia, diminuindo assim as suas vibraes, o que aumenta a sua efetividade.
No caso c) da Fig. 3.9, em virtude da necessidade do vibrador ser suspenso a partir da
estrutura, torna-se obrigatrio que entre eles se providencie um bom isolamento, fornecendo
frequncias naturais de corpo rgido as mais baixas possveis.
Finalmente o caso d) da mesma figura vem trazer uma situao no satisfatria, pois a base
do vibrador est diretamente em contato com a estrutura. Logo as foras provocadas pelo
vibrador vo atingir a estrutura em dois pontos distintos, o que no permitido, quando se mede
uma FRF comum.

3.4 Funes resposta em frequncia sistema de um grau de liberdade

Seja o sistema massa/mola/amortecedor viscoso apresentado na Fig. 3.10.

Figura 3.10: Sistema massa/mola/amortecedor viscoso.

Admitindo a aplicao de uma fora harmnica, na forma f(t) = F e
iet
, como o sistema
linear, a resposta em regime permanente apresentar a mesma frequncia, ou seja, x(t) = X e
iet
.
Ser agora determinada a receptncia, que a funo resposta em frequncia obtida pela relao
entre as amplitudes do deslocamento resultante e da fora aplicada. Atravs de um
desenvolvimento simples [ver, por exemplo, 1], chega-se a:


c i m k
1
F
X
2
e + e
= . (3.2)

Pode-se verificar que a Eq. (3.2) semelhante Eq. (1.49), que representa a receptncia
para cada um dos modos de vibrao de um sistema com vrios graus de liberdade, com
amortecimento do tipo proporcional. A diferena que na Eq. (1.49) esto sendo utilizados o
deslocamento e a fora generalizados. A Eq. (3.2) poderia ainda ser comparada, tambm, a uma
equao obtida a partir da Eq. (1.83), ao se isolar a relao
i
g i
F / P . O que ocorre, neste caso em
que o amortecimento no do tipo proporcional, o aparecimento de termos a
i
e b
i
complexos,
ao passo que na Eq. (3.2) os valores que lhes so correspondentes (c e k - me
2
) so reais.
Adicionalmente, com base na Eq. (2.52) seria possvel, considerando movimento
harmnico (q
r
(t) = Q
r
e
iet
e
r r
q q
F ) t ( f = e
iet
), obter uma equao semelhante Eq. (3.2), ao
se calcular a relao Q
r
/
r
q
F . Porm, no estudo de vibraes foradas de sistemas contnuos, o
fator relativo ao amortecimento no foi considerado, portanto o termo imaginrio iec que
aparece na Eq. (3.2) no teria um equivalente.
A Eq. (3.2) fornece valores complexos, e portanto pode ser representada de vrias
maneiras. Na Fig. 3.11 so apresentadas duas curvas, uma do mdulo e outra da fase.

43


Figura 3.11: Mdulo e fase da relao X/F, Eq. (3.2).

A relao X/F da Eq. (3.2) tambm pode ser apresentada atravs de duas curvas,
mostrando respectivamente as partes real e imaginria como funes da frequncia ( Fig. 3.12).


Figura 3.12: Partes real e imaginria da relao X/F, Eq. (3.2)

Finalmente, pode-se desenhar uma curva mostrando a parte imaginria versus a parte
real, como na Fig. 3.13.

Figura 3.13: Parte imaginria x parte real da relao X/F, Eq. (3.2).
44

As Figs. 3.11, 3.12 e 3.13 nada mais so do que representaes distintas (nos ltimos dois
casos so projees) da curva tridimensional que aparece na Fig. 3.14.


Figura 3.14: Representao tridimensional da relao X/F, Eq. (3.2).

A curva da Fig. 3.13 se assemelha a uma circunferncia. Entretanto pode-se provar
matematicamente que, no caso de amortecimento viscoso, a circunferncia perfeita s obtida
para a mobilidade (relao entre as amplitudes da velocidade resultante e da fora aplicada -
F / X

), dada por:

c i m k
i
F
X i
F
X
2
e + e
e
=
e
=

. (3.3)

A curva da parte imaginria versus a parte real da mobilidade est mostrada na Fig. 3.15.
Percebe-se que a multiplicao por i fez a posio da curva girar em 90

, com relao curva da

Fig. 3.13 (referente inertncia).

Figura 3.15: Parte imaginria x parte real da relao X

/F , Eq. (3.3).
45

Existe ainda uma outra funo resposta em frequncia, que a inertncia, obtida pela
relao entre as amplitudes da acelerao resultante e da fora aplicada que, no caso de um
sistema com um grau de liberdade com amortecimento viscoso, assim se apresenta:

c i m k F
X
F
X
2
2 2
e + e
e
=
e
=

. (3.4)

Se for desenhado um grfico do mdulo da Eq. (3.3), em torno da regio de ressonncia, na
forma log-log, tem-se uma curva como aquela mostrada na Fig. 3.16.
Figura 3.16: Curva de | F / X |

em torno da ressonncia,
indicando-se a banda de meia potncia.

Na Fig. 3.16 fica interessante definir a banda de meia potncia, que limitada pelas
frequncias e
b
e e
a.
Estas duas frequncias so obtidas traando-se uma linha horizontal que se
situa 3 dB abaixo do pico da curva. O fator de amortecimento viscoso pode ento ser estimado
pela equao:

0 0
b a
2 2 e
e A
=
e
e e
= , , (3.5)
onde e
0
a frequncia relativa ao pico.
Voltando a analisar a Eq. (3.2) e a primeira curva da Fig. 3.11 (ou seja, |X/F|), verifica-se
que em baixas frequncias, na subida inicial da curva, prevalece o termo 1/k (real positivo), e
diz-se que nesta regio a resposta dominada pela rigidez. Em altas frequncias, na regio final
de descida da curva, prevalece 1/(me
2
), que um termo real negativo. Diz-se que esta regio
dominada pela massa. Para frequncias em torno da frequncia natural amortecida, os termos de
rigidez e de massa se anulam, sobrando essencialmente o termo i/(ec), que imaginrio
negativo. Alm disto este ltimo termo depende essencialmente do amortecimento, e portanto
diz-se que a regio de ressonncia (pico) dominada pelo amortecimento.

3.5 Funes resposta em frequncia sistemas com vrios graus de liberdade

Quando se analisa um sistema com vrias massas, molas e amortecedores, ou ento um
sistema contnuo (tal como uma viga), iro aparecer respectivamente vrias ou infinitas
frequncias naturais, como j visto nos Captulos 1 e 2. Se for determinada a mobilidade,
aplicando-se fora num ponto da estrutura e medindo-se a velocidade neste ou em outro ponto,
para cada frequncia natural aparecer um pico na correspondente curva do mdulo. Alm
disso, para cada frequncia natural haver um termo semelhante quele que aparece na
Eq. (3.3), e a equao da mobilidade ser ento o somatrio destes termos (ver Fig. 3.17, onde h
um exemplo com trs termos e a correspondente soma).
46

Figura 3.17: Contribuio das trs frequncias naturais
e soma (linha cheia).

Pode-se entender agora que cada FRF de um sistema complexo constituda de vrios
picos. Com relao parte inicial da curva, ela decorre do tipo de fixao que se promove sobre
a pea. Se a estrutura est livre, em baixas frequncias ela se comporta como se fosse
simplesmente uma massa, portanto a FRF deve comear com uma regio de decaimento (ver
Fig. 3.18, curva a)). Se a estrutura est fixa, o seu comportamento em baixas frequncias
semelhante ao de uma mola, portanto a FRF deve iniciar com uma regio de valores crescentes
(ver Fig. 3.18, curva b)).


Figura 3.18: Anlise da regio inicial da FRF; a) pea livre e b) pea fixa.

As frequncias naturais so caractersticas de toda a estrutura, portanto a princpio elas
devem aparecer em todas as FRFs medidas sobre a mesma. Nas correspondentes formas de
modo h pontos que no se movimentam, chamados de ns. Se o acelermetro, por
coincidncia, for colocado sobre um n de um modo e for medida uma FRF, o pico na curva
correspondente a este modo em particular no aparecer.
Como exemplo, seja uma corda esticada, na qual sejam analisadas as vibraes
transversais, que vai apresentar infinitas frequncias naturais e correspondentes formas de modo
(Captulo 2),. Como ilustrao, na Fig. 3.19, so mostradas as formas dos trs primeiros modos.
Na primeira forma FM

1 no h n, na segunda FM

2 tem-se um n e na terceira FM 3

dois ns.

Figura 3.19: Formas dos trs primeiros modos de
uma corda esticada vibrando transversalmente.
47

Para entender de forma simples como estas formas so obtidas a partir das FRFs, imagine-
se que estas curvas sejam basicamente reais, com regies positivas e negativas. Seja ento a Fig.
3.20, na qual so mostradas as FRFs sobre linhas traadas a partir dos pontos da viga onde elas
foram medidas. Portanto, sobre estas linhas que partem da viga, tem-se os eixos das frequncias.
Numa dada frequncia natural, praticamente todas as FRFs vo mostrar picos, ora positivos, ora
negativos. Se para esta frequncia os correspondentes picos forem unidos por linhas, tem-se um
esboo da forma do modo de vibrao em questo.


Figura 3.20: Obteno das formas de modo a partir das FRFs.

Para que se possam entender algumas caractersticas de FRFs, ser agora apresentada
uma equao para a mobilidade deduzida na referncia [11], sendo que no desenvolvimento da
mesma se considerou o tipo mais simples de amortecimento viscoso (proporcional):

) 2 i ( m
) ( ) ( i
c i m k
) ( ) ( i
) ( Y
r r
2 2
r r
k r j r
N
1 r
N
1 r
r
2
r r
k r j r
k j
e e , + e e
e
=
e + e
e
= e

= =




= =
e e , + e e
e
=
e e , + e e
| | e
=
N
1 r
r r
2 2
r
k
j r
r r
2 2
r
k r j r
N
1 r
2 i
A i
2 i
) ( ) ( i
, (3.6)

onde j o ponto da estrutura onde se aplicou a fora e k o ponto onde o deslocamento foi
medido. O ndice r identifica o modo de vibrao ao qual o parmetro em questo se refere,
havendo neste caso um total de N modos. Deve-se perceber a semelhana da Eq. (3.6) com a
Eq. (3.3), sendo que esta corresponde a um sistema de um nico modo de vibrao. Para melhor
explicar os parmetros
r
|
j
e
r
|
k
, seja a Fig. 3.21 abaixo. Tem-se que
r
| a forma normalizada do
r-simo modo, sendo que
r
|
j
a amplitude do movimento no ponto j de aplicao da fora e, de
forma semelhante,
r
|
k
a amplitude no ponto k de resposta. De forma semelhante, na Eq. (3.6),
r
a forma modal no normalizada.
Na Eq. (3.6), o parmetro
r
A
jk
(resduo ou constante modal) o fator que indica se a
participao do r-simo modo na curva vai ser mais ou menos importante. Tem-se que
r
A
jk
vai
se anular se
r
|
j
= 0 e/ou
r
|
k
= 0. Isto significa que o r-simo modo no ativado, naquela FRF,
se o ponto de aplicao da fora e/ou o ponto de localizao do acelermetro for um ponto de n
da correspondente forma de vibrao.
48


Figura 3.21: Identificao de
r
|
j
e
r
|
k
.

Se o amortecimento for ainda considerado do tipo viscoso proporcional, os valores de
r
|
j
e
r
|
k
, e consequentemente de
r
A
jk
, so reais, podendo ser negativos ou positivos. No caso da
Fig. 3.21, se
r
|
j
considerado positivo,
r
|
k
ser negativo, e o produto resulta negativo.
Sejam agora analisados dois modos vizinhos, 1 e 2, com constantes
1
A
jk
e
2
A
jk
positivas.
Como j discutido anteriormente, cada curva de ressonncia possui a parte inicial crescente, com
valores predominantemente reais positivos. Na parte final acontece o contrrio: curva
decrescente, com valores predominantemente reais negativos. Na soma dos dois picos, na regio
central, existe ento o cancelamento, e vai aparecer uma anti-ressonncia (ver Fig. 3.22).

Figura 3.22: Soma de dois picos com ambas constantes positivas.

Se, em outra situao, a constante
1
A
jk
positiva e
2
A
jk
negativa, a segunda curva inverte a
polaridade, iniciando negativa e terminando positiva. Na parte central ambas as curvas sero
negativas, os valores se somaro, e no lugar da ressonncia do caso anterior vai aparecer um
vale (ver Fig. 3.23).

Figura 3.23: Soma de dois picos com constantes positiva e negativa

Quando se mede uma FRF pontual (fora e resposta no mesmo ponto), tem-se todos
r
A
jj
=
r
|
j
2
, portanto todas estas constantes so positivas (considerando que a forma modal
r
| seja
49

basicamente real, com valores positivos ou negativos). Ento cada ressonncia que entra no
somatrio vai iniciar real positiva e terminar real negativa. Portanto sempre entre dois picos as
duas curvas vizinhas vo se anular, formando uma anti-ressonncia. Esta , consequentemente,
uma caracterstica marcante de uma FRF pontual: entre todos os picos de ressonncia vai haver
sempre uma anti-ressonncia. Para uma FRF de transferncia (fora e resposta em posies
diferentes), quanto mais distantes os sensores, maior a incidncia de vales na curva.
Ao se fazer um teste modal, so identificados para cada r-simo modo os valores
r
A
jk
=
r
|
j

r
|
k
.

Se a fora aplicada sempre no mesmo ponto, tem-se
r
|
j
constante. Se, por sua
vez, o sensor da resposta mantido fixo, tem-se
r
|
k
constante. Da FRF pontual, obtm-se o
elemento constante,
r
|
j
=
j j r
A ou
r
|
k
=
k k r
A (ver pargrafo anterior). Uma vez que o
elemento constante conhecido, pode-se imediatamente calcular os elementos variveis, e com
eles compor a forma de vibrao do modo sob anlise.

3.6 Mtodos de extrao de parmetros modais

So analisados a seguir alguns mtodos de determinao dos parmetros modais, os quais
so, para cada modo analisado: frequncia natural, coeficiente (ou fator, ou razo) de
amortecimento e forma de modo.
O primeiro mtodo a ser apresentado um mtodo mais simples, que analisa os picos no
mdulo da FRF como se cada um deles fosse a resposta de um sistema de um grau de liberdade,
no havendo a interferncia dos demais. Para que este mtodo d bons resultados, ento,
necessrio que cada pico na curva esteja bem definido, relativamente bastante afastado dos
demais. Para tanto exige-se que o amortecimento, de uma forma geral, seja baixo, permitindo
ento que, realmente, na regio de anlise, o pico sob estudo tenha uma importncia
substancialmente maior que os demais.
Como nestes casos os picos de ressonncia so bem definidos, as frequncias naturais (e
r
)
so tomadas como aquelas correspondentes aos mesmos. Os fatores de amortecimento (,
r
)
podem ser calculados com base na banda de meia potncia (ver Fig. 3.16). O valor mximo da
curva (pico) do mdulo da FRF quando e bastante prximo a e
r
, identificado como | Y

|.
Admitindo e = e
r
na Eq. (3.6), obtm-se:


r r
k j r
2
A
| Y

|
e ,
= , (3.7)
ou:

r r k j r
2 | Y

| A e , = . (3.8)

Com os valores de
r
A
jk
ento possvel determinar a forma de vibrar do modo (ver ltimo
pargrafo da seo anterior).
Pelo processo acima, foi possvel ento determinar, para cada jk-sima FRF, os
parmetros: N frequncias naturais (e
r
), N fatores de amortecimento (,
r
) e N constantes
r
A
jk
. As
frequncias naturais e fatores de amortecimento modais podem ser tomados como os valores
mdios obtidos para as vrias curvas, ao passo que todos os
r
A
jk
so usados para calcular as
formas modais de vibrao. Como foi admitido baixo amortecimento, todas as constantes
r
A
jk

acabaram adotando valores reais.
A preciso deste primeiro mtodo no muito elevada, mas muitas vezes ele usado para
gerar uma estimativa inicial dos parmetros modais para auxiliar a aplicao de mtodos mais
complexos.
O segundo mtodo baseado no ajuste do crculo que traado no diagrama de Nyquist
(quando se traa a parte imaginria em funo da parte real, como na Fig. 3.15).
50

Voltando Eq. (3.6), levando em conta que, nas frequncias em torno do pico do r-simo
modo, normalmente a influncia dos outro modos pequena, e que esta pode ser substituda por
uma constante complexa, tem-se:

k
j r
r r
2 2
r
k
j r
k j
B
2 i
A i
) ( Y +
e e , + e e
e
= e . (3.9)

A influncia deste termo deslocar o crculo (ver Fig. 3.24), de forma que ele j no se
encontra encostado na origem como visto na Fig. 3.15.

Figura 3.24: Crculo deslocado pela soma de termo constante.

Por outro lado, o parmetro
r
A
jk
tambm influi na geometria do crculo, alterando o seu
dimetro e modificando a posio angular, como se pode ver na Fig. 3.25.


Figura 3.25: Crculo deslocado pela multiplicao de
r
A
jk
complexo.

Neste processo, a frequncia natural do modo (e
r
) determinada como sendo o ponto,
no crculo, onde h a maior variao de posio angular para um mesmo acrscimo Ae. Em
outras palavras, onde se verifica a maior distncia entre pontos consecutivos da curva (ver
Fig. 3.26).

Figura 3.26: Identificao de e
r
.
51

interessante verificar, na Fig. 3.26, que esto traados em torno de cem pontos do
crculo, mas que apenas sete deles, identificados com marcas escuras, cobrem mais da metade do
crculo. A frequncia natural onde ocorre o maior ngulo entre dois pontos da curva, supondo
que todos esto igualmente espaados em frequncia.
Para identificar o amortecimento do modo, seja analisada a Fig. 3.27 abaixo, onde, por
simplicidade, o crculo foi mantido junto origem.

Figura 3.27: Parmetros auxiliares para calcular o amortecimento.

O amortecimento dado por:

,
r
= (e
a
2
- e
b
2
) / (2 e
r
(e
a
tg(u
a
/2) + e
b
tg(u
b
/2)) , (3.10)

ou, para baixo amortecimento:

,
r
= (e
a
- e
b
) / (e
r
(tg(u
a
/2) + tg(u
b
/2)) . (3.11)

Se u
a
= u
b
= 90
o
(pontos de meia potncia), tem-se o valor exato:

,
r
= (e
a
- e
b
) / 2e
r
. (3.12)

Identificada a frequncia natural e
r
(conforme o procedimento ilustrado na Fig. 3.26) e
calculado o coeficiente de amortecimento (atravs das equaes logo acima), resta calcular o
valor de
r
A
jk
. Comparando um crculo modificado e um crculo original (multiplicado ou no
por
r
A
jk
), como aqueles que aparecem na Fig. 3.25, pode-se deduzir a seguinte relao, que
permite calcular o mdulo da constante complexa
r
A
jk
:


k
j r r r
k
j r
D 2 A e , = , (3.13)

onde
r
D
jk
o dimetro do crculo sob anlise. O ngulo de fase de
r
A
jk
o ngulo que o
dimetro principal do crculo, o qual passa pelo ponto correspondente a e
r
, faz com o eixo
positivo de Re[Y], como se pode ver na Fig. 3.25.

3.7 Termos residuais de baixa e alta frequncias

Ao se analisar uma certa faixa intermediria de frequncias, que envolve alguns modos de
vibrao, h a interferncia dos modos inferiores e superiores. Sero agora apresentados dois
termos, chamados de termos residuais, os quais so funes da frequncia, que simulam tais
interferncias na faixa sob estudo.
Pelo mesmo motivo j apresentado anteriormente, qual seja, o comportamento mais
equilibrado, sero agora aqui trabalhadas as mobilidades, com amortecimento do tipo viscoso.
52

Portanto, buscando a Eq. (3.6):

=
e e , + e e
e
= = e
N
1 r
r r
2 2
r
k
j r
jk
2 i
A i
) ( Y . (3.14)

O somatrio da Eq. (3.14) agora sub-dividido em trs regies: a inferior, a de interesse e
a superior, conforme a diviso indicada na Fig. 3.28.
Figura 3.28: Definio de regies da FRF.

Em termos de equao, a diviso assim se apresenta:


=

=
e e , + e e
e
+
e e , + e e
e
= e
2
1
1
m
m r
r r
2 2
r
k
j r
1 m
1 r
r r
2 2
r
k
j r
jk
2 i
A i
2 i
A i
) ( Y

+ =
e e , + e e
e
N
1 m r
r r
2 2
r
k
j r
2
2 i
A i
. (3.15)

Na Fig. 3.29 foram representados isoladamente os trs somatrios que aparecem na
Eq. (3.15). O que pode perceber claramente que os modos da regio inferior contribuem, na
regio central, de interesse, com uma funo proporcional a 1/e. Os modos da regio superior,
por sua vez, interferem na regio central como uma funo proporcional a e.

Figura 3.29: Contribuio dos modos: a) inferiores,
b) de interesse e c) superiores.
53

Como consequncia, os modos fora da faixa de interesse podem ser simplificadamente
representados por dois termos matemticos, os termos residuais, um com comportamento de
massa e outro com comportamento de rigidez, sendo que ento a Eq. (3.15) pode ser rescrita da
seguinte maneira:

jk K
m
m r
r r
2 2
r
k
j r
jk M
2
jk
R
i
2 i
A i
R
i
) ( Y
2
1
e
+
e e , + e e
e
+
e
e
= e

=
, (3.16)

onde as constantes
M
R
jk
e
K
R
jk
so a massa e a rigidez residuais para aquela faixa de interesse.
Se os limites desta se alteram, os valores das constantes sero outros.
O clculo dos valores de
M
R
jk
e
K
R
jk
baseado nas diferenas entre a curva original (que
envolve todos os modos, com r de 1 a N) e a curva que regenerada a partir das constantes
modais identificadas, somente para os modos com r de m
1
e m
2
. A curva regenerada nada mais
do que o resultado apenas do somatrio que aparece na Eq. (3.16).
Na Fig. 3.30 esto indicadas, de forma sombreada, as regies que so reproduzidas com o
auxlio das constantes
M
R
jk
( esquerda) e
K
R
jk
( direita).

Figura 3.30: Diferenas entre a FRF original e a FRF regenerada
parcialmente, na regio de interesse.

Os termos residuais so mais importantes quando as FRFs so pontuais. Nestes casos as
constantes modais apresentam todas elas um formato semelhante. Se fossem nmeros reais, por
exemplo, seriam todas positivas. Como consequncia, tomando a Fig. 3.29, curva a), para
raciocinar, todas as contribuies dos modos da regio inferior sobre a regio de interesse
apresentam fases semelhantes, havendo sempre a soma construtiva das mesmas. Para uma FRF
de transferncia, as constantes modais podem apresentar fases opostas, de forma que suas
contribuies podem vir a se cancelar, resultando em uma importncia menor dos termos
residuais.














54

CAPTULO 4: Mecnica analtica

As leis de Newton foram formuladas para uma partcula nica, podendo ser estendidas para
sistemas de partculas e corpos rgidos. Elas so baseadas em deslocamentos e foras,
quantidades que podem ser representadas por vetores, da a denominao de mecnica vetorial.
Porm, muitas vezes o clculo das foras complicado e, alm disso, elas no devem aparecer
nas equaes de movimento.
Como alternativa surge a mecnica analtica, que trata o sistema como um todo, atravs
de duas funes escalares: a energia cintica e a energia potencial. Os problemas so formulados
em termos de coordenadas e foras generalizadas, as quais muitas vezes no tm significado
fsico. Assim, a formulao matemtica independe de qualquer sistema particular de
coordenadas. So bastante utilizados os deslocamentos virtuais, que levam ao clculo de
variaes. Da a razo, tambm, de se usar para este estudo a designao mecnica variacional.
Neste captulo so inicialmente revistos conceitos como trabalho e energia, sendo
posteriormente apresentados os princpios do trabalho virtual e de dAlembert. Na sequncia
apresentado o ncleo deste captulo, as equaes de movimento de Lagrange. Finalmente so
derivadas as equaes diferenciais relativas s vibraes de sistemas discretos lineares, com o
auxlio das equaes de Lagrange [2,5,8].

4.1 Trabalho e energia

Seja uma partcula de massa m se movendo sobre uma curva s, sob a ao de uma fora F,
conforme a Fig. 4.1. No h restries aplicadas a este movimento. O acrscimo infinitesimal
de trabalho relacionado ao movimento de m, da posio r posio r+dr, dado pelo produto
escalar:
dW = F dr . (4.1)
Figura 4.1: Trabalho realizado ao longo de dr.

A segunda lei de Newton, para a partcula, fornece: F = m r . Lembrando que dt / dr r =
e que dt / dr r = , a Eq. (4.1) pode ser reescrita como:

dW = F dr = m r dr = m r dr = d ( m r r ) = dT . (4.2)

A funo T a energia cintica, dada por:

T = m r r = m
2
r , (4.3)

onde r a magnitude do vetor r . Deve-se notar que T uma funo escalar.
55

Se a partcula se move da posio
1
r para a posio
2
r sob a fora F, ento o trabalho
realizado :

1 2 1 1 2 2
T T
2
1
2
1
d
2
1
= =
}
r r r r r F
r
r
m m . (4.4)

Em alguns problemas fsicos a fora depende apenas da posio, F = F(r), e ento F dr
resulta uma funo simplesmente de r. Assim, pode-se escrever:

dW = F dr = - dV(r) , (4.5)

onde V(r) uma funo escalar, denominada energia potencial. Portanto tem-se W = - V, onde
W conhecida como funo trabalho. Combinando agora as Eqs. (4.2) e (4.5) se obtm:

d(T + V) = 0 . (4.6)

A soma da energia cintica e da energia potencial fornece a energia total do sistema, E.
Integrando a Eq. (4.7) se obtm:

T + V = E = cte , (4.7)

que estabelece que a energia total do sistema constante. A Eq. (4.7) conhecida como o
princpio da conservao de energia, e o campo de foras F dito conservativo.
Como dW na Eq. (4.5) diferencivel, usando-se coordenadas cartesianas possvel obter:

F dr = - dV = |
.
|

\
|
c
c
+
c
c
+
c
c
dz
z
V
dy
y
V
dx
x
V
= - VV dr , (4.8)
onde
V = k j i
z y x c
c
+
c
c
+
c
c
(4.9)

o operador nabla. A Eq. (4.8) implica em que:

F = - VV (4.10)

que, em outras palavras, significa que o vetor fora o gradiente negativo da energia potencial.
Decompondo em coordenadas cartesianas, tem-se: F
x
= - cV/cx, F
y
= - cV/cy e F
z
= - cV/cz.
As foras que atuam sobre uma partcula podem ser divididas em conservativas e no
conservativas, ou seja:
F = F
c
+ F
nc
. (4.11)

Verificando que a Eq. (4.5) vlida somente para foras conservativas, considerando a
Eq. (4.2) e aplicando o produto escalar de toda a Eq. (4.11) por dr, obtida a equao:

d (T + V) = dE = F
nc
dr , (4.12)

que, dividida por dt, fornece:

r F = = +
nc
dt
dE
) V T (
dt
d
, (4.13)

que estabelece que a taxa de trabalho realizado pelas foras no conservativas igual taxa de
variao da energia total do sistema.
56

4.2 O princpio do trabalho virtual

Este princpio estabelece o equilbrio de um sistema mecnico, sendo que para apresent-lo
necessrio definir os deslocamentos virtuais.
Seja um sistema com N partculas no espao tridimensional. H portanto 3N
deslocamentos de translao possveis: x
1
, y
1
, z
1
, x
2
, ... , z
N
. Os deslocamentos virtuais so ento
as variaes aplicadas a estes deslocamentos, ox
1
, oy
1
, oz
1
, ox
2
, ... , oz
N
, variaes estas que
devem ser compatveis com os vnculos aplicados ao sistema. Os deslocamentos virtuais no so
deslocamentos reais, mas pequenas variaes nas coordenadas que se obtm imaginando-se que
o sistema assumiu uma nova posio levemente modificada. Considera-se que eles ocorram
simultaneamente.
Se as coordenadas reais satisfazem equao de restrio:

g(x
1
, y
1
, z
1
, x
2
, ... , z
N
,t) = c , (4.14)

ento os deslocamentos virtuais devem ser tais que:

g(x
1
+ox
1
, y
1
+oy
1
, z
1
+oz
1
, x
2
+ox
2
, ... , z
N
+ox
N
,t) = c . (4.15)

Expandindo a Eq. (4.15) em uma srie de Taylor, se obtm:

g(x
1
, y
1
, z
1
, x
2
, ... , z
N
,t) +

=
|
.
|

\
|
o
c
c
+ o
c
c
+ o
c
c
N
1 i
i
i
i
i
i
i
z
z
g
y
y
g
x
x
g
= c , (4.16)
e portanto:

=
|
.
|

\
|
o
c
c
+ o
c
c
+ o
c
c
N
1 i
i
i
i
i
i
i
z
z
g
y
y
g
x
x
g
= 0 . (4.17)

A Eq. (4.17) implica em que apenas 3N 1 deslocamentos virtuais so arbitrrios. Em
geral, o nmero de deslocamentos virtuais arbitrrios coincide com o nmero de graus de
liberdade do sistema.
Admite-se que cada uma das N partculas pertencentes ao sistema seja sujeita seguinte
fora resultante:
R
i
= F
i
+ f
i
, i = 1, 2, ..., N , (4.18)

onde F
i
a fora aplicada e f
i
a fora de restrio. Exemplos de foras aplicadas: gravitacionais,
magnticas, aerodinmicas, etc ... As foras de restrio so aquelas de natureza reativa, que
normalmente aparecem quando algum movimento do sistema impedido.
Para um sistema em equilbrio, a fora aplicada sobre cada partcula deve se anular, ou
seja, R
i
= 0. Assim, os produtos escalares R
i
or
i
, onde or
i
= ox
i
i + oy
i
j + oz
i
k (i = 1, 2, ... ,N)
so os deslocamentos virtuais, tambm devem se anular. Mas R
i
or
i
representa o trabalho
virtual efetuado pela fora resultante na i-sima partcula quando ocorre o deslocamento virtual
or
i
. Somando as parcelas, o trabalho virtual total dado por:

=
= o = o
N
1 i
i
0 W r R
i
. (4.19)
Inserindo a Eq. (4.18) na Eq. (4.19), obtm-se:



= =
= o + o = o
N
1 i
i
N
1 i
i
0 W r f r F
i i
. (4.20)
57

Na Eq. (4.20), o segundo somatrio resulta nulo, pois as foras de restrio so
normalmente ortogonais aos deslocamentos virtuais, uma vez que estes movimentos so aqueles
admitidos pelo sistema. Assim, a Eq. (4.20) se reduz a:

=
= o = o
N
1 i
i
0 W r F
i
, (4.21)

ou seja, o princpio do trabalho virtual estabelece que o trabalho efetuado pelas foras
aplicadas, ao longo de deslocamentos virtuais compatveis com os vnculos do sistema, nulo.

Exemplo:

a) Duas barras, ambas de comprimento L, encontram-se originalmente na posio
horizontal, sendo que a mola, de constante de rigidez k, no est neste momento
exercendo qualquer fora sobre elas. ento aplicada uma massa m no ponto de unio
das barras conforme a Fig. 4.2. Deseja-se calcular a posio de equilbrio, definida pelo
ngulo u.
Figura 4.2: Sistema de duas barras e mola do exemplo.

Da anlise geomtrica, as distncias x e y da Fig. 4.2 so dadas por:

x = 2 L (1 - cos u) e y = L sen u . (4.22)

As foras aplicadas sobre o sistema composto por duas barras so as reaes na
extremidade da esquerda, a reao vertical (fora de restrio) sobre a extremidade da
direita, a fora de mola kx e o peso mg. Como a extremidade da esquerda no admite
deslocamentos e a fora de restrio na extremidade direita perpendicular ao
movimento possvel x, tem-se que o trabalho total virtual dado por:

oW = - kx o
x
+ mg o
y
= 0 , (4.23)

onde o produto kx o
x
aparece com sinal negativo pois a fora de mola kx e o
deslocamento virtual o
x
apresentam sentidos contrrios.
Diferenciando as Eqs. (4.22) so obtidos:

o
x
= 2 L sen u o
u
e o
y
= L cos u o
u
, (4.24)

que, levados Eq. (4.23), juntamente com a primeira das Eqs. (4.22), fornecem:

- k [2 L (1 cos u) ] (2 L sen u o
u
) + mg (L cos u o
u
) = 0 , (4.25)

cujo resultado final a equao transcendental:

(1 cos u) tg u = (mg) / (4kL) . (4.26)
58

4.3 O princpio de dAlembert

O principio do trabalho virtual, analisado na Seo anterior, trata apenas de problemas
estticos. O princpio de dAlembert estabelece uma extenso para problemas dinmicos.
Aplicando a segunda lei de Newton a cada uma das partculas do sistema, lembrando da
Eq. (4.18), pode-se escrever:

F
i
+ f
i
- m
i

i
r = 0 , i = 1, 2, ..., N . (4.27)

O trabalho virtual para a i-sima partcula ento dado por:

( F
i
+ f
i
- m
i

i
r ) or
i
= 0 , i = 1, 2, ..., N . (4.28)

Se os deslocamentos virtuais or
i
so compatveis com as restries do sistema, tem-se que
o trabalho virtual total dado por:

=
= o
N
1 i
i i i
0 ) m ( r r F
i
. (4.29)

A Eq. (4.29) conhecida como o princpio generalizado de dAlembert. A parcela
F
i
- m
i
i
r denominada, algumas vezes, como a fora efetiva.
Podem agora ser resolvidos problemas dinmicos, mas a formulao acima no muito
conveniente porque os problemas so formulados em termos das coordenadas de posio, que
podem no ser todas independentes.

4.4 As equaes de movimento de Lagrange

As coordenadas fsicas r
i
(i = 1, 2, ... , N) nem sempre so independentes. , portanto,
conveniente escrever as equaes do movimento atravs de coordenadas generalizadas
independentes q
k
(k = 1, 2, ... , n). Aplica-se ento uma transformao de coordenadas e, com o
auxlio do princpio de dAlembert, obtm-se tais equaes, conhecidas como as equaes de
movimento de Lagrange.
Admitindo-se que as coordenadas r
i
no dependem explicitamente do tempo e
considerando um sistema com n graus de liberdade, pode-se escrever a transformao de
coordenadas na forma geral:

r
i
= r
i
(q
1
, q
2
, ... , q
n
) , i = 1, 2, ... , N . (4.30)

As velocidades podem ser determinadas pela obteno da derivada total com relao ao
tempo das Eqs. (4.30), o que fornece:

=
c
c
=
c
c
+ +
c
c
+
c
c
=
n
1 k
k
k
i
n
n
i
2
2
i
1
1
i
i
q
q
q
q
q
q
q
q

r r r r
r , i = 1, 2, ... , N . (4.31)

Como as grandezas c r
i
/ c q
k
no dependem explicitamente das velocidades generalizadas
k
q , as Eqs. (4.31) fornecem:


k
i
k
i
q q c
c
=
c
c r r

, i = 1, 2, ... , N; k = 1, 2, ... , n . (4.32)

59

Em analogia com a Eq. (4.31) pode-se escrever:

=
o
c
c
= o
c
c
+ + o
c
c
+ o
c
c
= o
n
1 k
k
k
i
n
n
i
2
2
i
1
1
i
i
q
q
q
q
q
q
q
q
r r r r
r , i = 1, 2, ... , N . (4.33)

Levando em considerao as Eqs. (4.33), o segundo termo da Eq. (4.29) se apresenta agora
na seguinte forma:

k
n
1 k
N
1 i k
i
i i
N
1 i
n
1 k
k
k
i
i i
N
1 i
i i i
q
q
m q
q
m m o |
.
|

\
|
c
c
= o
c
c
= o

= = = = =
r
r
r
r r r . (4.34)

Analisando um termo tpico que aparece na Eq. (4.34), dentro dos parnteses, se obtm:

|
.
|

\
|
c
c
|
.
|

\
|
c
c
=
c
c

k
i
i i
k
i
i i
k
i
i i
q dt
d
m
q
m
dt
d
q
m
r
r
r
r
r
r . (4.35)

Aplicando a ltima derivada temporal que aparece na Eq. (4.35), chega-se a:


|
.
|

\
|

c
c
|
.
|

\
|
c
c
=
c
c
|
.
|

\
|
c
c
=
c
c

i i i
k k k
i
i i
k
i
i i
k
i
i i
m
2
1
q q dt
d
q
m
q
m
dt
d
q
m r r
r
r
r
r
r
r

. (4.36)

Na Eq. (4.36), o termo no interior dos ltimos parnteses a energia cintica da i-sima
partcula. Portanto, levando a Eq. (4.36) Eq. (4.34) obtm-se:

k
n
1 k
N
1 i
i i i
k k
N
1 i
i i i
q m
2
1
q q dt
d
m o
)
`

|
.
|

\
|

c
c
|
.
|

\
|
c
c
= o

= = =
r r r r

k
k k
n
1 k
q
q
T
q
T
dt
d
o
(

c
c
|
.
|

\
|
c
c
=

=

, (4.37)
onde:
) q , ... , q , q , q , ... , q , q ( T m
2
1
T
n 2 1 n 2 1
N
1 i
i i i
= =

=
r r (4.38)

a energia cintica de todo o sistema.
necessrio escrever as foras F
i
em termos das coordenadas generalizadas q
k
. Isto
obtido com o auxlio da expresso do trabalho virtual, mais a transformao indicada na
Eq. (4.33), o que fornece:



= = = = =
o |
.
|

\
|
c
c
= o
c
c
= o = o
N
1 i
N
1 i
n
1 k
k
N
1 i k
i
n
1 k
k
k
i
i
q
q
q
q
W
r
F
r
F r F
i i i
. (4.39)

O trabalho virtual, entretanto, pode ser considerado como o produto de n foras
generalizadas Q
k
atuando ao longo dos deslocamentos virtuais oq
k
, ou seja:

=
o = o
n
1 k
k k
q Q W . (4.40)
Comparando as Eqs. (4.39) e (4.40), conclui-se que as foras generalizadas possuem a
forma:

=
c
c
=
N
1 i k
i
k
q
Q
r
F
i
, k = 1, 2, ... , n. (4.41)
Em situaes reais as foras generalizadas so derivadas pela identificao fsica de um
conjunto de coordenadas generalizadas e o trabalho virtual calculado atravs da Eq. (4.40), e
60

no atravs da Eq. (4.41). As foras generalizadas no precisam ser necessariamente foras.
Podem ser momentos, ou quaisquer outras grandezas, desde que o produto Q
k
oq
k
possua
unidades de trabalho.
Se as foras que agem sobre o sistema podem ser divididas em conservativas, as quais
podem ser derivadas da energia potencial V, e no conservativas, que no podem, ento o
primeiro termo da Eq. (4.29) fica na forma:



= =
o + o = o + o = o = o
n
1 k
k knc
N
1 i
nc c i
q Q V W W W r F
i

=
o + |
.
|

\
|
o
c
c
+ + o
c
c
+ o
c
c
=
n
1 k
k knc n
n
2
2
1
1
q Q q
q
V
q
q
V
q
q
V

=
o |
.
|

\
|

c
c
=
n
1 k
k knc
k
q Q
q
V
, (4.42)

onde Q
knc
(k = 1, 2, ... , n) so as foras generalizadas no conservativas.
Levando as Eqs. (4.37) e (4.42) Eq. (4.29), obtm-se:

0 q Q
q
V
q
T
q
T
dt
d
k knc
k k k
n
1 k
= o
(

c
c
+
c
c
|
.
|

\
|
c
c

. (4.43)

Como os valores de oq
k
so arbitrrios, a Eq. (4.43) s pode ser verdadeira se todos os
termos entre parnteses se anularem, ou seja, se:


knc
k k k
Q
q
V
q
T
q
T
dt
d
=
c
c
+
c
c
|
.
|

\
|
c
c

, k = 1, 2, ... , n , (4.44)

que so as famosas equaes de movimento de Lagrange.
Em geral a energia potencial V no depende das velocidades generalizadas
k
q (k = 1, 2, ... ,
n). Pode-se ento definir o Lagrangeano como:

L = T - V , (4.45)
e assim a Eq. (4.44) se transforma em:


knc
k k
Q
q
L
q
L
dt
d
=
c
c
|
.
|

\
|
c
c

, k = 1, 2, ... , n . (4.46)

Tendo em vista a necessidade de serem consideradas tambm as foras no conservativas
(ligadas dissipao de energia, por parte do sistema), deve-se introduzir uma funo,
denominada funo de dissipao de Rayleigh, na forma:

= =
=
n
1 r
n
1 s
s r rs
q q c
2
1
F , (4.47)

na qual os coeficientes constantes c
rs
so simtricos com relao aos ndices r e s.
Ao gerar a funo que aparece na Eq. (4.47) admitiu-se que as foras de amortecimento
so proporcionais s velocidades generalizadas. Assim agora podem-se determinar foras de
amortecimento viscoso de forma anloga quela utilizada para as foras conservativas, ou seja:

k
knc
q
Q
c
c
=
F
, k = 1, 2, ... , n . (4.48)
61

Admitindo que as foras no conservativas que aparecem na Eq. (4.46) possam ser
divididas em foras de amortecimento viscoso, dadas pela Eq. (4.48), e outras causadas por
fatores externos (atravs das foras externas Q
k
), a Eq. (4.46) pode ser assim reescrita:


k
k k k
Q
q q
L
q
L
dt
d
=
c
c
+
c
c

|
|
.
|

\
|
c
c

F
, k = 1, 2, ... , n . (4.49)

Quando no h qualquer fora no conservativa, ou seja, quando o sistema perfeitamente
conservativo, as equaes de Lagrange se resumem a:

0
q
L
q
L
dt
d
k k
=
c
c
|
.
|

\
|
c
c

, k = 1, 2, ... , n . (4.50)

4.5 As equaes de movimento de Lagrange para sistemas lineares

A inteno aqui analisar o movimento de um sistema de vrios graus de liberdade nas
vizinhanas de sua posio de equilbrio. Se os deslocamentos generalizados so
suficientemente pequenos, as relaes lineares fora/deslocamento e fora/velocidade se mantm
e as coordenadas generalizadas e suas derivadas temporais aparecem nas equaes diferenciais
de movimento na primeira potncia. Esta a condio conhecida como de pequenos
deslocamentos, que fornece um sistema linear de equaes.
Como no se admitem potncias superiores unidade nas equaes diferenciais, os
coeficientes cr
i
/cq
k
, nas Eqs. (4.31), devem ser constantes e no funes das coordenadas
generalizadas. Levando a transformao indicada na Eq. (4.31) Eq. (4.38), a energia cintica
do sistema assim se apresenta:

|
.
|

\
|
c
c
|
.
|

\
|
c
c
= =

= = = =
n
1 s
s
s
i
N
1 i
n
1 r
r
r
i
i
N
1 i
i i i
q
q
q
q
m
2
1
m
2
1
T
r r
r r



= = = = =
= |
.
|

\
|
c
c

c
c
=
n
1 r
s r
n
1 s
rs
n
1 r
s r
n
1 s
N
1 i s
i
r
i
i
q q m
2
1
q q
q q
m
2
1

r r
, (4.51)

onde

sr
N
1 i s
i
r
i
i rs
m
q q
m m =
c
c

c
c
=

=
r r
, r, s = 1, 2, ... , n (4.52)

so os coeficientes de massa constantes, ou coeficientes de inrcia.
A energia potencial na apareceu na Seo 4.4 de forma explcita, mas na forma geral
V = V(q
1
, q
2
, ... , q
n
). A expanso desta energia em srie de Taylor, em torno da posio de
equilbrio (q
1
= q
2
= ... = q
n
= 0), fornece:


n
n
2
2
1
1
n 2 1
q
q
V
q
q
V
q
q
V
) q , ... , q , q ( V
c
c
+ +
c
c
+
c
c
=


2 1
2 1
2
2
n
2
n
2
2
2
2
2
2
2
1
2
1
2
q q
q q
V
2 q
q
V
q
q
V
q
q
V
2
1
c c
c
+

\
|
c
c
+ +
c
c
+
c
c
+

+ |
.
|
c c
c
+ +
c c
c
+

n 1 n
n 1 n
2
3 1
3 1
2
q q
q q
V
2 q q
q q
V
2 . (4.53)
62

Na equao acima todas as derivadas parciais de V so avaliadas no ponto de equilbrio e
portanto so constantes. As derivadas primeiras cV/cq
k
representam as foras conservativas, que
so nulas na posio de equilbrio, o que fornece cV/cq
k
= 0 (k = 1, 2, ... , n). Desconsiderando
os termos de ordem superior a dois, a Eq. (4.53) se torna ento:



= = = =
=
c c
c
=
n
1 r
s r
n
1 s
rs
n
1 r
s r
n
1 s s r
2
q q k
2
1
q q
q q
V
2
1
V , (4.54)
onde

sr
r s
2
s r
2
rs
k
q q
V
q q
V
k =
c c
c
=
c c
c
= , r, s = 1, 2, ... , n (4.55)

so os coeficientes constantes simtricos identificados como coeficientes de rigidez.
Neste ponto se tem tanto as energias cintica e potencial como a funo de dissipao de
Rayleigh na forma denominada quadrtica. Pode-se ento aplicar a Eq. (4.49). Como a energia
potencial V no envolve as velocidade generalizadas, tem-se:

=
=
c
c
=
c
c
n
1 s
s js
j j
q m
q
T
q
L

, j = 1, 2, ... , n . (4.56)

De forma semelhante, se obtm:

=
=
c
c
=
c
c
n
1 s
s js
j j
q k
q
V
q
L
, j = 1, 2, ... , n (4.57)
e

=
=
c
c
n
1 s
s js
j
q c
q

F
, j = 1, 2, ... , n (4.58)

Levando as Eqs. (4.56), (4.57) e (4.58) Eq. (4.49) se obtm as equaes de Lagrange para
um sistema linear geral:

| | ) t ( Q ) t ( q k ) t ( q c ) t ( q m
j
n
1 s
s js s js s js
= + +

=
, j = 1, 2, ... , n . (4.59)

As Eqs. (4.59) so idnticas quelas que teriam sido obtidas com o auxlio da segunda lei
de Newton. Agrupando-as em forma matricial, chega-se a:

| |{ } | |{ } | |{ } { } ) t ( Q ) t ( q k ) t ( q c ) t ( q m = + + , (4.60)

onde [m], [c] e [k] so respectivamente as matrizes de inrcia, amortecimento e rigidez, todas
elas simtricas.

Exemplo:

a) Seja o sistema com trs massas ligadas por molas e amortecedores da Fig. 4.3. Neste caso
as coordenadas generalizadas q
1
(t), q
2
(t) e q
3
(t) so os prprios movimentos horizontais de
translao das massas. Para aplicar as equaes de Lagrange necessrio calcular o
Lagrangeano e a funo de dissipao de Rayleigh. A energia cintica total facilmente
calculada atravs de:

( )
2
3 3
2
2 2
2
1 1
q m q m q m
2
1
T + + = . (4.61)
63


Figura 4.3: Sistema de trs graus de liberdade.

As deformaes nas molas k
1
, k
2
e k
3
so respectivamente iguais a: q
1
, q
2
q
1
e
q
3
q
2
. Assim, a energia potencial total dada por:

| |
2
2 3 3
2
1 2 2
2
1 1
) q q ( k ) q q ( k q k
2
1
V + + =

| |
3 2 3 2 1 2
2
3 3
2
2 3 2
2
1 2 1
q q k 2 q q k 2 q k q ) k k ( q ) k k (
2
1
+ + + + = . (4.62)

Por analogia, a funo dissipao de Rayleigh dada por:

| |
3 2 3 2 1 2
2
3 3
2
2 3 2
2
1 2 1
q q c 2 q q c 2 q c q ) c c ( q ) c c (
2
1
+ + + + = F . (4.63)

Para derivar as equaes do movimento de Lagrange deve-se tomar L = T V,
aplicar as devidas derivadas s Eqs. (4.61), (4.62) e (4.63) e inserir os resultados na
Eq. (4.49). Porm todo este trabalho j foi implicitamente realizado na deduo da
equao matricial, Eq. (4.60), de forma a fornecer neste exemplo as matrizes abaixo:

| |
(
(
(

=
3
2
1
m 0 0
0 m 0
0 0 m
m , (4.64)

| |
(
(
(

+
+
=
3 3
3 3 2 2
2 2 1
c c 0
c c c c
0 c c c
c , (4.65)

| |
(
(
(

+
+
=
3 3
3 3 2 2
2 2 1
k k 0
k k k k
0 k k k
k . (4.66)

Estas matrizes so exatamente iguais quelas desenvolvidas no exemplo da
Seo 1.1, do Captulo 1 desta apostila, onde se aplicou a segunda lei de Newton na
obteno das equaes diferenciais de movimento do mesmo sistema fsico.





64

APNDICE A: Equao da onda seu desenvolvimento para alguns casos fsicos.

A equao da onda desenvolvida para vigas unidimensionais, sob trs tipos de
solicitao: foras axiais, toro e flexo. Neste ltimo caso obtida uma equao diferencial
no exatamente na forma da equao da onda, pois apresenta uma derivada quarta com relao
varivel espacial, mas ela semelhante e possui resoluo equivalente quela equao. So
apresentados tambm os desenvolvimentos da equao da onda nos casos da vibrao transversal
de cabo sujeito a tenso axial e da propagao unidimensional de som em duto. As condies de
contorno aplicveis a todos estes casos so tambm apresentadas [2,4,15,16].

A.1 - Vibrao axial em vigas

Seja um elemento infinitesimal de viga, comprimento dx, conforme a figura A.1 abaixo,
que est sujeito a cargas axiais. A rea da seo transversal da viga dada por A(x), a sua massa
por unidade de comprimento por m(x) e o mdulo de elasticidade do material por E(x). Neste
caso u(x,t) o movimento axial de uma dada seo transversal.

Figura A.1: Elemento infinitesimal sob a ao de cargas axiais.

Aplicando a 2
a
Lei de Newton ao movimento longitudinal:

E F = M a = M u , (A.1)
tem-se:

2
2
t
) t , x ( u
dx ) x ( m ) t , x ( P dx
x
) t , x ( P
) t , x ( P
c
c
=
(

c
c
+ . (A.2)

Eliminando dx, lembrando que a fora axial dada por P(x,t) = o(x,t) A(x) =
E(x) c
x
(x,t) A(x), e que c
x
(x,t)

= c u(x,t) / cx, tem-se:


2
2
t
) t , x ( u
) x ( m
x
) t , x ( u
) x ( A ) x ( E
x c
c
=
(

c
c
c
c
. (A.3)

Admitindo que E(x), A(x) e m(x) so constantes ao longo da viga, com valores E, A e
m, tem-se:

2
2
2 2
2
t
) t , x ( u
a
1
x
) t , x ( u
c
c
=
c
c
, (A.4)

que uma equao do tipo equao da onda, onde a
2
= E A / m .

65

Exemplo de condies de contorno espaciais:

Seja uma viga com propriedades constantes, com uma extremidade fixa e com uma massa
concentrada M
c
na sua outra extremidade, conforme a figura A.2.



Figura A.2: Exemplo de viga com extremidades fixa e com massa concentrada.

Tem-se neste caso a equao diferencial parcial recm desenvolvida, com as condies de
contorno espaciais:
u(0,t) = 0
e (A.5)
-E A u
x
(L,t) = M
c
u
tt
(L,t) .

Esta ltima condio de contorno obtida aplicando a 2
a
Lei de Newton massa M
c
,
lembrando que a fora axial dada por P(x,t) = E A u
x
(x,t).
Aplica-se separao de variveis com u(x,t) = X(x) T(t), e a equao da onda resulta assim:

' ' T X
a
1
T ' ' X
2
= , (A.6)
ou
= =
T
' ' T
a
1
X
' ' X
2
. (A.7)

Usando a mesma separao de variveis, as condies de contorno acima fornecem:

u(0,t) = X(0) T(t) = 0 ou X(0) = 0
e (A.8)
-E A X(L) T(t) = M
c
X(L) T(t) .

Mas, pela equao da onda, tem-se T / T = a
2
, e portanto esta ltima equao fica na
forma:

- E A X(L) = M
c
a
2
X(L) , (A.9)
ou
(L) ' X
a M
A E
- X(L)
2
c

= . (A.10)



66

Analisando o problema em X(x), tem-se a equao diferencial ordinria:

X(x) - X(x) = 0 , (A.11)

mais as condies de contorno (A.8) acima desenvolvidas, em x = 0 e x = L.
Este problema s admite, para > 0, solues triviais (nulas). Ento, para < 0, tem-se
a proposta de soluo:
) x cos( C ) x sen( C ) x ( X
2 1
+ = . (A.12)

Aplicando a primeira condio de contorno:

X(0) = 0 => C
2
= 0. (A.13)

Sobra portanto
) x sen( C ) x ( X
1
= , (A.14)
com a derivada
) x cos( C ) x ( ' X
1
= . (A.15)

Aplicando agora a segunda condio de contorno em x, tem-se:

) L cos( C
a M
A E
) L sen( C
1
2
c
1

= , (A.16)
e, fazendo v = L , introduzindo tambm o valor de a
2
, obtm-se a equao transcendental:


v
1
M
L m
v tg
c
= . (A.17)

Resolvendo a equao transcendental acima so obtidos valores de v
n
, que permitem
calcular os autovalores:

2
2
n
n
L
v
= , n = 1, 2, 3, ... . (A.18)

Retornando equao de X(x), so obtidas as autofunes:


L
x v
sen ) x ( X
n
n
= , n = 1, 2, 3, ... . (A.19)

Na soluo de T(t) deve-se buscar a equao T - a
2
T = 0, sendo que substituindo-se o
valor de tem-se:
0 ) t ( T
L
a v
) t ( ' ' T
2
2 2
n
= + , (A.20)

cuja soluo fornece:


|
.
|

\
|
+
|
.
|

\
|
=
L
t a v
sen D
L
t a v
cos D ) t ( T
n
n 2
n
n 1 n
. (A.21)

67

Assim, a autofuno de x e de t, ligada a cada autovalor
n
= - v
n
2
/ L
2
, dada por:


(

|
.
|

\
|
+
|
.
|

\
|
|
.
|

\
|
=
L
t a v
sen D
L
t a v
cos D
L
x v
sen ) t , x ( u
n
n 2
n
n 1
n
n
. (A.22)

Finalmente tem-se a soluo final admitindo a srie:

=
=
1 n
n
) t , x ( u ) t , x ( u , (A.23)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de deslocamento
e de velocidade da viga (condies iniciais).

A.2 - Vibrao torcional em vigas

Seja um elemento infinitesimal de viga de seo circular (ou seo em forma de anel), de
comprimento dx, conforme a figura A.3 abaixo, que est sujeito a torques. O momento polar de
inrcia da seo transversal da viga dado por J(x), o seu momento polar de inrcia de massa por
unidade de comprimento por i
m
(x) e o mdulo de elasticidade transversal do material por G(x).
Tem-se que u(x,t) o movimento de rotao de uma dada seo transversal.


Figura A.3: Elemento infinitesimal sob a ao de torques.

Aplicando a 2
a
Lei de Newton ao movimento torcional:

E T = I o = I u

, (A.24)
tem-se:
2
2
m
t
) t , x (
dx ) x ( i ) t , x ( T dx
x
) t , x ( T
) t , x ( T
c
u c
=
(

c
c
+ . (A.25)

Lembrando que o torque aplicado T(x,t) = J(x) t
mx
(x,t) / r(x) = J(x) G(x)
mx
(x,t) / r(x)
(onde r(x) o raio externo), que
mx
(x,t)

/ r(x) = c u(x,t) / cx, e eliminando dx, tem-se:


2
2
m
t
) t , x (
) x ( i
x
) t , x (
) x ( J ) x ( G
x c
u c
=
(

c
u c
c
c
. (A.26)

68

Admitindo que G(x), J(x) e i
m
(x) so constantes ao longo da viga, com valores G, J e i
m

respectivamente, tem-se:
2
2
2 2
2
t
) t , x (
a
1
x
) t , x (
c
u c
=
c
u c
, (A.27)

que uma equao do tipo equao da onda, onde a
2
= G J / i
m
.

Exemplo de condies de contorno espaciais:

Seja uma viga com propriedades constantes, com uma extremidade fixa e outra livre,
conforme a figura A.4.
Tem-se neste caso a equao diferencial parcial recm desenvolvida, com as condies de
contorno espaciais:
u(0,t) = 0
e (A.28)
T(L,t) = G J u
x
(L,t) = 0 .



Figura A.4: Exemplo de viga com extremidades fixa e livre.

Aplica-se separao de variveis com u(x,t) = X(x) T(t), e a equao da onda resulta
assim:

' ' T X
a
1
T ' ' X
2
= , (A.29)
ou
= =
T
' ' T
a
1
X
' ' X
2
. (A.30)

Usando a mesma separao de variveis, as condies de contorno acima fornecem:

u(0,t) = X(0) T(t) = 0 ou X(0) = 0
e (A.31)
u
x
(L,t) = X(L) T(t) = 0 ou X(L) = 0 .

Analisando o problema em X(x), tem-se a equao diferencial ordinria:

X(x) - X(x) = 0 , (A.32)

mais as condies de contorno (A.31) acima desenvolvidas, em x = 0 e x = L.
69

Este problema s admite, para > 0, solues triviais (nulas). Ento, para < 0, tem-se
a proposta de soluo:

) x cos( C ) x sen( C ) x ( X
2 1
+ = . (A.33)

Aplicando a primeira condio de contorno:

X(0) = 0 => C
2
= 0 . (A.34)

Sobra portanto
) x sen( C ) x ( X
1
= , (A.35)

com derivada
) x cos( C ) x ( ' X
1
= . (A.36)

Aplicando agora a segunda condio de contorno (A.31), obtm-se:

0 ) L cos( = , (A.37)
condio que obtida quando:

2
) 1 n 2 ( L
n
t
+ = , n = 0, 1, 2, ... (A.38)
ou
2
2 2
n
L 4
) 1 n 2 ( t +
= , n = 0, 1, 2, ... . (A.39)

Retornando equao de X(x), so obtidas as autofunes:


(

t +
=
L 2
x ) 1 n 2 (
sen ) x ( X
n
, n = 0, 1, 2, ... . (A.40)

Na soluo de T(t) deve-se buscar a equao T - a
2
T = 0 da Eq. (A.30), sendo que,
substituindo-se o valor de , tem-se:

0 ) t ( T
L 4
a ) 1 n 2 (
) t ( ' ' T
2
2 2 2
=
t +
+ , (A.41)
cuja soluo fornece:

(

t +
+
(

t +
=
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D ) t ( T
n 2 n 1 n
. (A.42)

Assim, a autofuno de x e de t, ligada a cada autovalor
n
, dada por:


)
`

t +
+
(

t +
(

t +
= u
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D
L 2
x ) 1 n 2 (
sen ) t , x (
n 2 n 1 n
. (A.43)


70

Finalmente tem-se a soluo final admitindo a srie:

=
u = u
0 n
n
) t , x ( ) t , x ( , (A.44)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de giro e de
velocidade angular da viga (condies iniciais).



A.3 - Vibrao transversal de cabos sob tenso

Seja um elemento infinitesimal de cabo, comprimento Ax, conforme a figura A.5
abaixo, o qual est sujeito originalmente ao de fora de tenso H. Considera-se que H seja
basicamente a nica carga que restaura o cabo posio original, ou seja, a flexo no tem
importncia nesta funo porque o cabo considerado extremamente flexvel. A massa por
unidade de comprimento do cabo dada por m(x). O movimento transversal de cada ponto
central do cabo dado por v(x,t).

Figura A.5: Elemento de cabo infinitesimal sob a ao de fora de tenso H.

A componente horizontal das foras T e T constante, ou seja:

T(x,t) cos[o(x,t)] = T(x,t) cos[o(x,t)] = H . (A.45)

Aplicando a 2
a
Lei de Newton ao movimento transversal do elemento de cabo:

T(x,t) sen[o(x,t)] - T(x,t) sen[o(x,t)] = m(x) Ax
2
2
t
) t , x ( v
c
c
. (A.46)

Dividindo a Eq. (A.46) por H (e valores equivalentes, ver Eq. (A.45)):


2
2
t
) t , x ( v
H
x ) x ( m
)] t , x ( cos[ ) t , x ( T
)] t , x ( sen[ ) t , x ( T
)] t , x ( cos[ ) t , x ( T
)] t , x ( sen[ ) t , x ( T
c
c A
=
o
o

o
o
. (A.47)


71

e simplificando:

2
2
t
) t , x ( v
H
x ) x ( m
)] t , x ( [ tg )] t , x ( [ tg
c
c A
= o o . (A.48)

Dividindo por Ax e lembrando que tg(o) = cv / cx, tem-se:


2
2
x x x
t
) t , x ( v
H
) x ( m
x
) t , x ( v
x
) t , x ( v
x
1
c
c
=
(

c
c

c
c
A
A +
(A.49)

e tomando o limite quando Ax 0, admitindo m(x) constante e igual a m, tem-se:


2
2
2 2
2
t
) t , x ( v
a
1
x
) t , x ( v
c
c
=
c
c
, (A.50)

onde a
2
= H / m . Esta ltima equao do tipo equao da onda.

Exemplo de condies de contorno espaciais:

Seja um cabo sob tenso com propriedades constantes, com duas extremidades fixas,
conforme a figura A.6.


Figura A.6: Exemplo de cabo sob tenso, com ambas as extremidades fixas.

Tem-se neste caso a equao diferencial parcial (A.50), com as condies de contorno
espaciais:

v(0,t) = 0
e (A.51)
v(L,t) = 0 .

Aplicando separao de variveis com v(x,t) = X(x) T(t), a equao da onda resultante
passa a se apresentar da seguinte forma:
' ' T X
a
1
T ' ' X
2
= , (A.52)
ou
= =
T
' ' T
a
1
X
' ' X
2
. (A.53)


72

Usando a mesma separao de variveis, as condies de contorno acima fornecem:

v(0,t) = X(0) T(t) = 0 ou X(0) = 0
e (A.54)
v(L,t) = X(L) T(t) = 0 ou X(L) = 0 .

Analisando o problema em X(x), de (A.53) obtm-se a equao diferencial ordinria:

X(x) - X(x) = 0 , (A.55)

mais as condies de contorno apresentadas em (A.54), em x = 0 e x = L.
Este problema s admite, para > 0, solues triviais (nulas). Ento, para < 0, tem-se
a proposta de soluo:
) x cos( C ) x sen( C ) x ( X
2 1
+ = . (A.56)

Aplicando a primeira condio de contorno (A.54):

X(0) = 0 => C
2
= 0 . (A.57)

Sobra portanto
) x sen( C ) x ( X
1
= . (A.58)

Aplicando agora a segunda condio de contorno (A.54) resulta:

X(L) = 0 => 0 ) L sen( = , (A.59)

condio que obtida quando:

t = n L
n
, n = , 1, 2, 3, ... (A.60)
ou

2
2 2
n
L
n t
= , n = 1, 2, 3, ... . (A.61)

Retornando equao de X(x), so obtidas as autofunes:

|
.
|

\
|
t
=
L
x n
sen ) x ( X
n
, n = 1, 2, 3, ... . (A.62)

Na soluo de T(t) deve-se buscar de (A.53) a equao T - a
2
T = 0, sendo que,
substituindo-se o valor de , tem-se:
0 ) t ( T
L
a n
) t ( ' ' T
2
2 2 2
=
t
+ , (A.63)
cuja soluo fornece:


|
.
|

\
|
t
+
|
.
|

\
|
t
=
L
t a n
sen D
L
t a n
cos D ) t ( T
n 2 n 1 n
. (A.64)


73

Assim, a autofuno de x e de t, ligada a cada autovalor
n
, dada por:


(

|
.
|

\
|
t
+
|
.
|

\
|
t
|
.
|

\
|
t
=
L
t a n
sen D
L
t a n
cos D
L
x n
sen ) t , x ( v
n 2 n 1 n
. (A.65)

Finalmente tem-se a soluo final admitindo a srie:

=
=
1 n
n
) t , x ( v ) t , x ( v , (A.66)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de deslocamento
lateral e de velocidade lateral dos pontos do cabo (condies iniciais).


A.4 - Vibrao transversal de flexo em vigas

Seja um elemento infinitesimal de viga, de comprimento dx, conforme a figura A.7 abaixo,
que est sujeito a momentos fletores e esforos cortantes. A rigidez de flexo da viga dada por
EI(x), onde E(x) o mdulo de elasticidade do material e I(x) o momento de inrcia da seo
transversal. m(x) a sua massa por unidade de comprimento. A teoria de vigas aqui apresentada
a de Bernoulli-Euler, mais simples, que no considera a inrcia rotatria e o cisalhamento.




Figura A.7: Elemento infinitesimal sob flexo.

Aplicando a 2
a
Lei de Newton ao movimento vertical deste elemento:

E F = M a = M v
tem-se:

2
2
t
) t , x ( v
dx ) x ( m ) t , x ( V dx
x
) t , x ( V
) t , x ( V
c
c
=
(

c
c
+ (A.67)
ou

2
2
t
) t , x ( v
) x ( m
x
) t , x ( V
c
c
=
c
c
. (A.68)



74

Desconsiderando o efeito de inrcia rotatria, a equao de equilbrio de momentos em
torno do ponto central da face esquerda fornece:

0 dx dx
x
) t , x ( V
) t , x ( V ) t , x ( M dx
x
) t , x ( M
) t , x ( M =
(

c
c
+ +
(

c
c
+ , (A.69)

e, simplificando e eliminando o termo em dx
2
(termo de segunda ordem), tem-se:

0 ) t , x ( V
x
) t , x ( M
= +
c
c
. (A.70)

Se a Eq. (A.70) levada Eq. (A.68), obtm-se:


2
2
2
2
t
) t , x ( v
) x ( m
x
) t , x ( M
c
c
=
c
c
. (A.71)

Da Mecnica dos Slidos, busca-se a equao simples que relaciona momento fletor
com o deslocamento transversal v(x,t):

2
2
x
) t , x ( v
) x ( EI ) t , x ( M
c
c
= . (A.72)

Inserindo a Eq.(A.72) em (A.71) obtm-se:


2
2
2
2
2
2
t
) t , x ( v
) x ( m
x
) t , x ( v
) x ( EI
x c
c
=
(

c
c
c
c
. (A.73)

Se EI(x) e m(x) so constantes ao longo da viga, com valores EI e m, tem-se:


2
2
4 4
4
t
) t , x ( v
a
1
x
) t , x ( v
c
c
=
c
c
, (A.74)

onde a
4
= E I / m.
A equao diferencial parcial (A.74) no se apresenta exatamente na forma de uma
equao da onda, pois a derivada espacial de quarta ordem (na equao da onda de segunda
ordem). Sendo assim, dado um certo segmento de viga, so necessrias quatro condies de
contorno espaciais, ao invs de duas como acontece quando se usa uma equao do tipo equao
da onda. Entretanto a maneira de obter uma soluo para este caso semelhante utilizada nas
equaes do tipo equao da onda.


Exemplo de condies de contorno espaciais:

Seja uma viga com propriedades constantes, com ambas as extremidades articuladas
(pinadas), conforme a figura A.8 abaixo.




75


Figura A.8: Exemplo de viga com ambas as extremidades articuladas (pinadas).

Tem-se neste caso a equao diferencial parcial recm desenvolvida, com as quatro
condies de contorno espaciais:

v(0,t) = 0
M(0,t) = E I v
xx
(0,t) = 0 (A.75)
v(L,t) = 0
M(L,t) = E I v
xx
(L,t) = 0

Aplica-se separao de variveis com v(x,t) = X(x) T(t), e a equao da onda resulta
assim:

' ' T X
a
1
T X
4
) IV (
= , (A.76)
ou
= =
T
' ' T
a
1
X
X
4
) IV (
. (A.77)

Usando a mesma separao de variveis, as condies de contorno acima fornecem:

v(0,t) = X(0) T(t) = 0 ou X(0) = 0
M(0) = E I X (0) T(t) = 0 ou X (0) = 0 (A.78)
v(L,t) = X(L) T(t) = 0 ou X(L) = 0
M(L) = E I X (L) T(t) = 0 ou X (L) = 0 .

Analisando o problema em X(x), de (A.77) obtm-se a equao diferencial ordinria:

X
(IV)
- X(x) = 0 , (A.79)

mais as condies de contorno (A.78), em x = 0 e x = L.
Este problema s admite, para s 0, solues triviais (nulas). Ento, para >0, tem-se
a proposta de soluo:

) x sen( C ) x cos( C ) x ( h sen C ) x ( h cos C ) x ( X
4
4
4
3
4
2
4
1
+ + + = , (A.80)

com derivada segunda:

) x sen( C ) x cos( C ) x ( h sen C ) x ( h cos C ) x ( ' ' X
4
4
4
3
4
2
4
1
+ = . (A.81)
76


Aplicando a primeira condio de contorno (A.78):

X(0) = 0 => C
1
+ C
3
= 0 . (A.82)

A segunda condio de contorno (A.78) fornece:

X(0) = 0 => 0 C C
3 1
= . (A.83)

Este sistema em C
1
e C
3
s fornece valores no nulos para estas constantes se 0 = , o
que implicaria em uma soluo trivial para o problema, portanto no desejada. Em
conseqncia, tem-se C
1
= C
3
= 0. Portanto a soluo fica na forma:

) x sen( C ) x ( h sen C ) x ( X
4
4
4
2
+ = . (A.84)

Aplicando agora a terceira condio de contorno (A.78):

X(L) = 0 => 0 ) L sen( C ) L ( h sen C
4
4
4
2
= + , (A.85)

e finalmente a quarta condio de contorno (A.78) fornece:

X (L) = 0 => 0 ) L sen( C ) L ( h sen C
4
4
4
2
= . (A.86)

Este sistema em C
2
e C
4
s vai possuir uma soluo no trivial (sendo que esta
significaria C
2
= C
4
= 0 , ou seja, soluo nula) se os coeficientes de C
2
e C
4
formarem uma
matriz singular, ou seja, com determinante nulo. Esta ltima condio nos leva equao:

0 ) L sen( ) L ( h sen 2
4 4
= . (A.87)

Fazendo 0 = ou 0 ) L ( h sen
4
= ter-se-ia a mesma soluo, j descartada, = 0.
Assim sendo, resta apenas considerar 0 ) L sen(
4
= , o que fornece:

t = n L
4
n
, n = 1, 2, 3, ... (A.88)
ou ento:

4
4 4
n
L
n t
= , n = 1, 2, 3, ... . (A.89)
Com 0 ) L ( sen
4
= , voltando s condies de contorno (A.85) e (A.86), obtm-se
C
2
= 0. Portanto as autofunes ficam simplesmente na forma:

|
.
|

\
|
t
=
L
x n
sen ) x ( X
n
, n = 1, 2, 3, ... . (A.90)

Na soluo de T(t) deve-se buscar a equao T + a
4
T = 0, a partir da Eq. (A.77),
sendo que substituindo-se o valor de tem-se:
0 ) t ( T
L
a n
) t ( ' ' T
4
4 4 4
=
t
+ , (A.91)

77

cuja soluo fornece:
|
.
|

\
| t
+ |
.
|

\
| t
=
2
2 2 2
n 2
2
2 2 2
n 1 n
L
t a n
sen D
L
t a n
cos D ) t ( T . (A.92)

Assim, a autofuno de x e de t, ligada a cada autovalor
n
, dada por:


(

|
.
|

\
| t
+ |
.
|

\
| t
|
.
|

\
|
t
=
2
2 2 2
n 2
2
2 2 2
n 1 n
L
t a n
sen D
L
t a n
cos D
L
x n
sen ) t , x ( v . (A.93)

Finalmente tem-se a soluo final admitindo a srie:

=
=
1 n
n
) t , x ( v ) t , x ( v , (A.94)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de deslocamento
transversal e de velocidade transversal dos pontos da viga (condies iniciais).

A.5 -Propagao de som em dutos (unidimensional)

Seja um fluido compressvel, como por exemplo o ar. Pode-se ento definir a condensao
s como sendo:

0
0 t
s

= . (A.95)
onde
t
a densidade instantnea em um ponto e
0
a correspondente densidade em equilbrio.
Toma-se agora um elemento de volume em um duto de seo transversal A, com
comprimento dx, conforme a figura A.9 abaixo. O elemento mostra seus contornos nas posies
originais (linhas tracejadas) e deslocadas (linhas contnuas).


Figura A.9: Elemento infinitesimal de volume de ar.

As massas totais dos elementos original e deformado devem ser iguais, logo:

dx A
x
u
1 dx A
0 t
= |
.
|

\
|
c
c
+ . (A.96)

78

Substituindo
t
pela equao obtida a partir da definio de s, simplificando
0
e A, tem-se:

1
x
u
1 ) s 1 ( = |
.
|

\
|
c
c
+ + . (A.97)

Para ondas sonoras no ar, tanto s como cu/ct assumem valores muito baixos (< 10
-4
), logo
o seu produto pode ser desprezado, obtendo-se assim:


x
u
s
c
c
= . (A.98)
As relaes entre presso e densidade podem ser dadas, para processo isotrmico, por:

|
.
|

\
|

=
0
t
0
t
p
p
, (A.99)
ou, para processo adiabtico, por:

|
.
|

\
|

=
0
t
0
t
p
p
, (A.100)

onde p
t
a presso instantnea em um ponto, p
0
a correspondente presso de equilbrio e a
razo calorfica do gs.
Admite-se a Eq. (A.100) como sendo a mais apropriada para expanses e compresses
causadas por ondas sonoras. Derivando-a ento em relao a
t
:

|
.
|

\
|

= |
.
|

\
|
c
c
0
t
t 0
1
t
t
t
0
p
p
1
, (A.101)
ou

2
t
t
t
t
c
p p
=

=
c
c
. (A.102)

Conclui-se posteriormente que c a velocidade do som no ar. Ento, para o ar em
equilbrio:

0
0 2
p
c

= . (A.103)
Por exemplo, para o ar a 0
o
tem-se p
0
= 1,013 . 10
5
N/m
2
,
0
= 1,293 kg/m
3
e = 1,402, o
que fornece c = 331,4 m/s.
Admitindo que p
t
uma funo a vrias variveis, dentre elas a densidade
t
, se somente
esta grandeza sofrer uma leve variao pode-se escrever a srie:

... d
p
! 2
1
d
p
p p
2
t
2
t
t
2
t
t
t
0 t
+
|
|
.
|

\
|
c
c
+ |
.
|

\
|
c
c
+ = . (A.104)

Na equao acima, desprezando os termos de maior ordem, tem-se aproximadamente:

t
t
t
0 t
d
p
p p |
.
|

\
|
c
c
= . (A.105)
79

Identificando p = p
t
- p
0
como a variao de presso provocada pelas ondas sonoras, e
fazendo d
t
=
t
-
0
= s
0
(ver equao no incio deste item), tem-se:


0
t
t
s
p
p |
.
|

\
|
c
c
= , (A.106)
ou
s c p
0
2
= , (A.107)

e finalmente, substituindo o valor de s (ver Eq. (A.98)):

x
u
c p
0
2
c
c
= . (A.108)
Aplicando a 2
a
Lei de Newton ao elemento de volume de ar que aparece na figura A.10,
desconsiderando a presso de equilbrio que atua em suas faces (esquerda e direita), tem-se a
equao:

2
2
0
t
u
dx A A dx
x
p
p p
c
c
=
(

|
.
|

\
|
c
c
+ , (A.109)

a qual fornece, aps simplificaes:

2
2
0
t
u
x
p
c
c
=
c
c
. (A.110)



Figura A.10: Desequilbrio de presses sobre o comprimento dx.

Combinando as Eqs. (A.108) e (A.110) so finalmente obtidas as equaes:


2
2
2 2
2
t
u
c
1
x
u
c
c
=
c
c
(A.111)
e

2
2
2 2
2
t
p
c
1
x
p
c
c
=
c
c
. (A.112)

Estas duas ltimas equaes so do tipo equao da onda, escritas respectivamente nas
variveis u e p.



80

Exemplo de condies de contorno espaciais:

Seja um tubo repleto de ar, com propriedades fsicas do ar e geomtricas do tubo
constantes, com uma extremidade fechada e outra aberta, conforme a figura A.11.

Figura A.11: Exemplo de tubo com ar, com extremidades fechada e aberta.

Tem-se neste caso a equao diferencial parcial recm desenvolvida, com as condies
de contorno espaciais:
u(0,t) = 0
e (A.113)
p(L,t) = - c
2

0
u
x
(L,t) = 0 .

Aplica-se separao de variveis com u(x,t) = X(x) T(t), e a equao da onda resulta
assim:

' ' T X
a
1
T ' ' X
2
= , (A.114)
ou
= =
T
' ' T
a
1
X
' ' X
2
. (A.115)

Usando a mesma separao de variveis, as condies de contorno acima fornecem:

u(0,t) = X(0) T(t) = 0 ou X(0) = 0
e (A.116)
u
x
(L,t) = X(L) T(t) = 0 ou X(L) = 0 .

Analisando o problema em X(x), da Eq. (A.115) obtm-se a equao diferencial
ordinria:
X(x) - X(x) = 0 (A.117)

mais as condies de contorno (A.116), em x = 0 e x = L.
Este problema s admite, para > 0, solues triviais (nulas). Ento, para < 0, tem-se
a proposta de soluo:
) x cos( C ) x sen( C ) x ( X
2 1
+ = . (A.118)

Aplicando a primeira condio de contorno (A.116):

X(0) = 0 => C
2
= 0. (A.119)

81

Sobra portanto
) x sen( C ) x ( X
1
= (A.120)
com derivada
) x cos( C ) x ( ' X
1
= . (A.121)

Aplicando agora a segunda condio de contorno (A.116) resulta:

0 ) L cos( = , (A.122)
condio que obtida quando:
2
) 1 n 2 ( L
n
t
+ = , n = 0, 1, 2, ... , (A.123)
ou


2
2 2
n
L 4
) 1 n 2 ( t +
= , n = 0, 1, 2, ... . (A.124)
Retornando equao de X(x), so obtidas as autofunes:


(

t +
=
L 2
x ) 1 n 2 (
sen ) x ( X
n
, n = 0, 1, 2, ... . (A.125)

Na soluo de T(t) deve-se buscar a equao T - a
2
T = 0, obtida da Eq. (A.115),
sendo que, substituindo-se o valor de , tem-se:

0 ) t ( T
L 4
a ) 1 n 2 (
) t ( ' ' T
2
2 2 2
=
t +
+ , (A.126)
cuja soluo fornece:
|
.
|

\
| t +
+ |
.
|

\
| t +
=
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D ) t ( T
n 2 n 1 n
. (A.127)

Assim, a autofuno de x e de t, ligada a cada autovalor
n
, dada por:

(

|
.
|

\
| t +
+ |
.
|

\
| t +
(

t +
=
L 2
t a ) 1 n 2 (
sen D
L 2
t a ) 1 n 2 (
cos D
L 2
x ) 1 n 2 (
sen ) t , x ( u
n 2 n 1 n
. (A.128)

Finalmente tem-se a soluo final admitindo a srie:

=
=
1 n
n
) t , x ( u ) t , x ( u , (A.129)

onde os valores de D
1n
e de D
2n
so obtidos em funo das distribuies iniciais de deslocamento
de partcula e de velocidade de partcula, no ar e no sentido axial, ao longo do tubo (condies
iniciais).





82

REFERNCIAS BIBLIOGRFICAS:

1. CORDIOLI, J. A.. Notas de Aula Disciplina EMC5140: Controle de Vibraes.
Brasil: UFSC, 2014.
2. MEIROVITCH, L.. Elements of Vibration Analysis. Second Edition. Singapura:
McGraw-Hill International Editions, 1975.
3. NEWLAND, D. E.. Mechanical Vibration Analysis and Computation. Inglaterra:
Longman Scientific and Technical, 1989. ISBN: 0-582-02744-6
4. REYNOLDS, D. D.. Engineering Principles of Acoustics. Estados Unidos da Amrica:
Allyn and Bacon, Inc.; 1981.
5. DIMAROGONAS, A.. Vibration for Engineers. Second Edition. Estados Unidos da
Amrica: Prentice Hall, 1995.
6. LALANNE, M., BERTHIER, P. e der HAGOPIAN, J.. Mechanical Vibrations for
Engineers. Irlanda: John Wiley & Sons Ltd., 1983. ISBN 0-471-90197-0.
7. STEIDEL Jr., R. F.. An Introduction to Mechanical Vibrations. Second Edition.
Estados Unidos da Amrica: John Wiley & Sons Ltd., 1979. ISBN: 0-471-82083-0.
8. THOMSON, W. T.. Teoria da Vibrao com aplicaes. Brasil: Editora Intercincia,
1978.
9. ALMEIDA, M. T.. Vibraes Mecnicas para Engenheiros. Brasil: Editora Edgar
Blcher Ltda, 1987.
10. GROEHS, A. G.. Mecnica Vibratria. Brasil: Editora Unisinos, 1999.
11. EWINS, D. J.. Modal Testing: Theory and Practice. Inglaterra: Research Studies Press
Ltd., 1984. ISBN: 0-86380-017-3.
12. MAIA, Nuno M. M. et al. Theoretical and Experimental Modal Analysis. Inglaterra:
Research Studies Press Ltd., 1997. ISBN: 0-86380-208-7.
13. KREIDER, D. L.; KULLER, R. G.; OSTBERG, D. R. e PERKINS, F.W.. An
Introduction to Linear Analisys. Estados Unidos da Amrica: Addison-Wesley
Publishing Co., 1966.
14. PESTEL, E. C.; LECKIE, F. A.. Matrix Methods in Elastomechanics. Estados Unidos
da Amrica: McGraw-Hill Book Company, Inc., 1963.
15. GERGES, S. N. Y.. Rudo: Fundamentos e Controle. 2
a
edio. Brasil: NR Editora,
2000. ISBN 85-900046-01-x.
16. PIERCE, Allan D.. Acoustics: An Introduction to Its Physical Principles and
Applications. Estados Unidos da Amrica : McGraw-Hill Book Co., 1981. ISBN 0-07-
049961-6.