Professional Documents
Culture Documents
Series
Series
Uploaded by
Anonymous GNWnQac0 ratings0% found this document useful (0 votes)
24 views7 pagesseries
Copyright
© © All Rights Reserved
Available Formats
PDF or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Documentseries
Copyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
0 ratings0% found this document useful (0 votes)
24 views7 pagesSeries
Series
Uploaded by
Anonymous GNWnQacseries
Copyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
You are on page 1of 7
The Basie Tests for Infinite Series
(W Divergence Test
Integral Test
(©) Comparison Test
(@) Limit Comperison Test
(© Retio and Root Tests
(9) Leibnie Test for Alternating Series
<=> PEMINDER The Leone Test states that
Stn comergsif the 00600 fn)
'S positive, decreasing, and im, an = 0.
This test doesnot apply to the series
Example 1 (because the terms
2
on rat
donot satisty either of te wo hypotheses:
(aa) isnot decreasing andi, an iS
F STRATEGIES FOR
TESTING SERIES
W ite consier many base comergenc et for infinite series in Chapter 11.
‘So given a particular infinite series, which test should you use? There is no single
answer, but there are some facts and general guidelines you should Keep in mind. First of
all, to develop your intuition, you should be familiar with the following key examples:
+ Geomen series: Sr" converges ifr] < 1 and diverges otherwise
os
«+ prseries: 37 converges if p > 1 and diverges otherwise
mt™
et
+ Y= converges by the Ratio Test.
yn
oor
converges conditionally but not absolutely Example 4, Section 11.4).
‘A frst step, when testing an innit series
isto check tat the general term ay approaches ero. By the Divergence Tet if lian
doesnot exist ori im, exists bat isnot equal to zero, then a diverges.
M1 EXAMPLE 1 First Check Whether the General Term Approaches Zero Determine the
Sa’ o2 (=1)"n4
‘convergence of (a) )—~— and (b) .
wai & mri
Solution Both series diverge:
a fener
© im = im pice = 1 ome) > SP aves
CV? 4,
ped a s
0) sig Po in LP, doesnot exisy = 3° SP iver
o
AM ee eT ene
Next, ask yourself if the series resembles a series whose behavior is known. If s0,
try using the Comparison or Limit Comparison Tests. The following guidelines may be
useful:
A
LATE TRANSCENDENTALS
APPENDIX F 1 STRATEGIES FOR TESTING SERIES
If the series conta Tey:
i orcther powers of Comparison or Limit Comparison with p-series|
PP (constant) Ratio Test
factorials such as n!, (2a)! Ratio Test
a Root Test
cy Check for absolute convergence or use Leibniz Test
EXAMPLE 2 Check for a Simple Comparison Determine the convergence of
¥
Term
1 1
Solution The series converges by the Comparison Test because Te———r S Tg
and So ig comersnt omer eres (win Z). atthoug te neal
nis alo mu, itcannot be used tots our sees because Jn
.
°Tetr
diverges.
Often there is more than one way of testing the convergence of a series. For example,
\we may prove thatthe following series converges in at least three ways:
Bt
lea
converges.
bmi AEs
1a
Tat Sat
2. Comparison Test wits 5°
a
3. Limit Compaion wit 3°: L = iy, 2m jim
ml 2
‘When a, = f(n) where f(x) is a rational or algebraic function, we may apply the
Limit Comparison Test with a p-series. Recall that the behavior of f(n) as n —> 00 is
‘determined by the highest powers of n appearing in the numerator and denominator.
WW EXAMPLE 3 Terms Defined by a Rational Function: Limit Comparison Determine the
An? +2n—9
comerene ofS = Laie
Solution
Step 1. Determine behavior of dy a8. —> 00.
“The highest powers of 1 in the numerator and denominator are n? and 7/7, s0 an
behaves like the ratio
4n? 4 a
on a = 5 an co.
LATE TRANSCENDENTALS
APPENDIX F | STRATEGIES FOR TESTING SERIES 2
“This suggests a limit comparison withthe p-seies “9.
> Step 2. Apply the Limait Comparison Test with by = n~*/?,
442-908
Tim St = fim
Deby ab
= tim AP +29
eto Tat ant 2 SP
4n?+2n~9
+» REMINDER By Theorem 1 in Section = jim 7 te
45, Ht das tm #0, then He THEE ST? = 29
(see marginal note)
Since L exists and 5 bn = .>n7¥7 isa convergent p-series, 5 ay also converges
et a
by the Limit Comparison Test .
EXAMPLE 4 Terms Defined by an Algebraic Function Linit Comparison Determine
SZ n2+2n-9
Lay
the convergence of "ae
Solution
Siep 1. Determine behavior of ay 85» 00.
‘Although the denominator (n7 + Sn®)"/? is an algebraic function rather than a poly-
‘nomial, its behavior is still determined by its leading term:
(0? 502) = (7h Sn)" =n (1 Sn“A'2
saqromtes Yas 00
Thus
4mn-9 an yoo
= GT eSB ~ I
Step 2. Apply the Limit Comparison Test with by = n@¥/3,
tim % = tim BESTE gg EMF 1
lin 5 = him, ie = A aT SB
a nb +2n-9 n?+2n—9 ‘ 1
= in, ta (um, *) (a)
since 1» Oma $2 ty Sn! ea degen paces, Sean so ery
the Limit Comparison Test. .
EXAMPLE 5 Series Involving Factorials: Ratio Test Determine the convergence of
210
© ws mS
" a
LATE TRANSCENDENTALS
APPENDIX F J STRATEGIES FOR TESTING SERIES
Note that for alt k,
wet at oe
im, = (aim. '
oe GE (#2. *
In Example 7, there are infinitely mony
ways of witing the general term as 2
‘procct ef 2 bounded term end n~? with
‘p> 3. For example, instead of (2), we may
write
ea) Gala
for some constant C. snee Sots 8
convergent pees, we conc again
that § also converges.
Solution The limit p is zero in both cases, so both series converge by the Ratio Test:
oor
fq _loont tnt 100
er fi, ToonGeH TD! ene
= tm 2 tn SEIT yy OE nt
(0) p= fi, Sm tim, EE = in
(52) (testa)? vee 7
‘A factorial in the denominator does not guarantee convergence, as the next example
shows.
EXAMPLE 6 Deteminethecomesenceof J" 2
am
Solution This series diverges by the Ratio Test because p is infinite:
a >
os
fim Stl tea é co
oe Jn ram iS e+
ethan? gan
ig = i =
= in Gat 7 eee i
‘ibs Roe
When the general term aq involves logarithms, we may use that fact that Inn grows
‘more slowly than n* for all k > 0. More precisely, it follows from L’Hépital’s Rulle that
WE <9 forall exponents @ and k > 0) o
Bonk
EXAMPLE 7 Determine the convergence of S = Ee
=
Solution The term n°/* im the denominator suggests comparison with a p-sries. We
camo compare with 5 tse? n pens inthe unto Hower, we can
still show that § converges by writing the general term of $ asa product:
qe
BA GIR DR
LATE TRANSCENDENTALS
APPENDIX F J STRATEGIES FOR TESTING SERIES 7
intn
Applying (1) with a = 2 and & = 1/8, we see that lim “77 = O. In particular, the
sequence {In? n/n'/8) is bounded by a constant C, and we obtain
1
we SC (am)
el Z 3,
since $° 1, ia convent p series the ses converges by compari.
Note, by contrast with Example 7, that
tan at
Loar serses (compare with 7)
=
itn
Indeed, itis easy to check that “Spt > —7 for n > 3. Since the p-series with p = 3/4
ma
diverges, cur series also diverge by the Comparison Test.
Exercises
Determine whether the series converges absolutely, converges condi-
tionally, or diverges, by any method.
a
Ms il
a
R
Me
i
i
2 in
et
LATE TRANSCENDENTALS
6 APPEWOIX F 4 STRATEGIES FOR TESTING SERIES
0 te Sn
2, 25n!0 + 50
we
&
Me IMs iM
2
Ms
=
¢
aoe
LATE TRANSCENDENTALS
Polutions to Appendix F Odd Exercises
1. converges
3. diverses
5. diverse
1 converges coniinsly
9 converges
11, cooverees
13, comers
1 diverges
1, verges
19. comers
21. comerees
28, converzesconitonlly
25, comernes
27, comerges
APPENDIX F | STRATEGIES FOR TESTING SERIES £7
29. comers
‘31. comerescondtionaly
133, comers aoltely
38, diverses
131. converses coniionaly
39, comers contol
41, diverges
You might also like
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Distance Time Graphs Worksheet PDFDocument5 pagesDistance Time Graphs Worksheet PDFAnonymous GNWnQacNo ratings yet
- Make The Grade As and A2 Chemistry Chemistry Revision Guide Edexcel As A2 Modular Nelson Advanced ScienceDocument147 pagesMake The Grade As and A2 Chemistry Chemistry Revision Guide Edexcel As A2 Modular Nelson Advanced Scienceareyouthere92100% (3)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- 0580 TopicalDocument589 pages0580 TopicalAnonymous Kx8TAybnXQ100% (1)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5810)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (844)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- Any Set of Points Represent A Linear Relation If They Form A Straight Line When Plotted On A GraphDocument3 pagesAny Set of Points Represent A Linear Relation If They Form A Straight Line When Plotted On A GraphAnonymous GNWnQacNo ratings yet
- c3 Numerical MethodsDocument7 pagesc3 Numerical MethodsAnonymous GNWnQacNo ratings yet
- s1 Normal DistributionDocument9 pagess1 Normal DistributionAnonymous GNWnQacNo ratings yet
- c1 Coordinate Geometry Notes PDFDocument1 pagec1 Coordinate Geometry Notes PDFAnonymous GNWnQac100% (1)
- c4 Partial and BinomialDocument3 pagesc4 Partial and BinomialAnonymous GNWnQacNo ratings yet
- Period, Amplitude and ShiftDocument2 pagesPeriod, Amplitude and ShiftAnonymous GNWnQacNo ratings yet
- Reducing Fractions To Lowest TermsDocument1 pageReducing Fractions To Lowest TermsAnonymous GNWnQacNo ratings yet
- Any Set of Points Represent A Linear Relation If They Form A Straight Line When Plotted On A GraphDocument3 pagesAny Set of Points Represent A Linear Relation If They Form A Straight Line When Plotted On A GraphAnonymous GNWnQacNo ratings yet
- Bridging GCSE and A Level MathsDocument147 pagesBridging GCSE and A Level MathsAnonymous GNWnQacNo ratings yet
- KWL Chart: Name: - DateDocument1 pageKWL Chart: Name: - DateAnonymous GNWnQacNo ratings yet
- Partial Diffrentiation and Mutiple IntegralsDocument79 pagesPartial Diffrentiation and Mutiple IntegralsAnonymous GNWnQacNo ratings yet
- Practice Examination Questions For Binomial ExpansionDocument9 pagesPractice Examination Questions For Binomial ExpansionAnonymous GNWnQacNo ratings yet
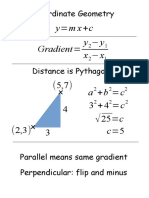
- Coordinate Geometry NotesDocument1 pageCoordinate Geometry NotesAnonymous GNWnQacNo ratings yet
- CubicGraphs FactorTheoremDocument18 pagesCubicGraphs FactorTheoremAnonymous GNWnQacNo ratings yet