Professional Documents
Culture Documents
Lesson 2: Conditional Probability
Lesson 2: Conditional Probability
Uploaded by
goserunnerOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Lesson 2: Conditional Probability
Lesson 2: Conditional Probability
Uploaded by
goserunnerCopyright:
Available Formats
Lesson 2
Conditional Probability
Probability and Binomial Distributions
Principles of Mathematics 12: Explained!
www.math12.com 328
Probability Lesson 2
Part 1: Conditional Probability
Conditional Probability: In many situations, the outcome of one event
will have a direct influence on the outcome of another event.
Such events are called dependent events.
Example 1: A person draws one card from a deck of 52 cards, then draws a second card.
Calculate the probability of both cards being clubs.
13 Drawing a card
The probability of drawing a club is without replacement
52 changes the
12 probability for the
The probability of drawing a second club is second card.
51
since there is one less club, and consequently Thus, the outcome of
one less card in the deck. the second card is
dependent on the
13 12 1 outcome of the first
The probability both cards are clubs is × =
52 51 17 card.
Example 2: A person draws one card from a deck of 52 cards, then returns it to the
deck. Another card is then drawn. Calculate the probability of both cards being clubs.
13
The probability of drawing a club is Replacing a card
52 returns the deck to
13 the initial state.
The probability of drawing a second club is
52
Thus, the outcome of
since the first card was put back in the deck. the second card is
independent from
13 12 1 the outcome of the
The probability both cards are clubs is × = first card.
52 51 16
The formula for conditional probability is:
P ( A and B ) = P ( A ) × P ( B|A )
The vertical line you see in the expression
P(B|A) is not a mathematical operation.
It is simply a reminder that you want the
probability of B, given that A has occurred.
Example 1 illustrates the use of this formula.
Principles of Mathematics 12: Explained!
www.math12.com 329
Probability Lesson 2
Part 1: Conditional Probability
Bayes’ Formula: The following is a manipulation of the formula introduced on
the previous page. It is used to find the conditional probability of Event B
occurring, given that Event A has already occurred.
P ( A and B )
P ( A|B ) =
P (B)
Example 3: A diagnostic test for liver disease is accurate 93% of the time, and 0.9% of
the population actually has liver disease.
a) Determine the probability the patient tests positive
b) Determine the probability the patient tests negative
c) Determine the probability the patient has liver disease and tests positive
d) Determine the probability the patient does not have liver disease and tests negative
First draw a tree diagram to determine all required probabilities:
Special care should
be taken when writing
in the probabilities, it’s
easy to mix up where
the positive tests &
negative tests go if
you too fast!
a) Add the probabilities where a positive result is obtained: 0.00837 + 0.06937 = 0.07774
b) Add the probabilities where a negative result is obtained: 0.00063 + 0.92163 = 0.92226
c) This question is asking you to solve d) This question is asking you to solve for
for P(liver disease | positive). P( no liver disease | negative).
Use Bayes’ Formula Use Bayes’ Formula
P ( A and B ) P ( A and B )
P ( A|B ) = P ( A|B ) =
P (B ) P (B )
P (liver disease and positive ) (
P no liver disease and negitive )
P ( liver disease | positive ) = ( )
P no liver disease | negative =
P (positive ) (
P negative )
0.00837 0.92163
P ( liver disease | positive ) = P ( no liver disease | negative ) =
0.07774 0.92226
P ( liver disease | positive ) = 0.10767 P ( no liver disease | negative ) = 0.99932
Principles of Mathematics 12: Explained!
www.math12.com 330
Probability Lesson 2
Part 1: Conditional Probability
Questions: 2) Cards are drawn from a standard
1) Cards are drawn from a standard deck of 52 cards with replacement.
deck of 52 cards without replacement. Calculate the probability of obtaining:
Calculate the probability of obtaining: a) A king, then another king
a) A king, then another king b) A club, then a heart
b) A club, then a heart c) A black card, then another black card
c) A black card, then another black card d) A black card, then a heart, then a
d) A black card, then a heart, then a diamond diamond
e) The seven of spades, then another spade, e) The seven of spades, then another
then a club, then a heart spade, then a club, then a heart
3) Given P(A) = 0.34, and P(B | A) = 0.65, calculate P(A & B)
4) Given P(A) = 0.2, P(B) = 0.8, P(A & B) = 0.1, calculate
a) P(A | B)
b) P(B | A)
5) A diagnostic test for eye disease is accurate 88% of the time, and 2.4% of the
population actually has eye disease.
a) Determine the probability the patient tests positive
b) Determine the probability the patient tests negative
c) Determine the probability the patient has eye disease and tests positive
d) Determine the probability the patient does not have eye disease and tests negative
Principles of Mathematics 12: Explained!
www.math12.com 331
Probability Lesson 2
Part 1: Conditional Probability
Answers:
1) 2)
4 3 1 4 4 1
a) × = a) × =
52 51 21 52 52 169
13 13 13 13 13 1
b) × = b) × =
52 51 204 52 52 16
26 25 25 26 26 1
c) × = c) × =
52 51 102 52 52 4
26 13 13 169 26 13 13 1
d) × × = d) × × =
52 51 50 5100 52 52 52 32
1 12 13 13 1 13 13 13
e) × × × = 0.000288 e) × × × = 0.0003
52 51 50 49 52 52 52 52
3) Use the formula P(A & B) = P(A) x P(B|A)
P(A & B) = 0.34 x 0.65
P(A & B) = 0.221
P ( A&B )
4) Use the formula P ( A|B ) =
P (B )
a) b)
P ( A&B ) P (B& A )
P ( A|B ) = P (B|A ) =
P (B ) P ( A)
0.1 0.1
P ( A|B ) = P (B|A ) =
0.8 0.2 a) Add up the cases with a positive result:
1 1 0.02122 + 0.11712 = 0.13834
P ( A|B ) = P (B|A ) =
8 2
b) Add up the cases with a negative result:
0.00288 + 0.85888 = 0.86176
c)
(
P Eye Disease & Positive )
5) Draw a tree diagram: ( )
P Eye Disease | Positive =
(
P Positive )
0.02122
( )
P Eye Disease | Positive =
0.13834
= 0.1534
d)
(
P No Disease & Negative )
(
P No Disease | Negative = )
(
P Negative )
0.85888
( )
P Eye Disease | Positive =
0.86176
= 0.9967
Principles of Mathematics 12: Explained!
www.math12.com 332
You might also like
- Member Stiffness and Contact Pressure Distribution of Bolted JointsDocument8 pagesMember Stiffness and Contact Pressure Distribution of Bolted JointsreaderScribd9100% (1)
- ATI TEAS Calculation Workbook: 300 Questions to Prepare for the TEAS (2023 Edition)From EverandATI TEAS Calculation Workbook: 300 Questions to Prepare for the TEAS (2023 Edition)No ratings yet
- Science To SageDocument81 pagesScience To SageAleksandra Kojic100% (1)
- Chapter 6 - ProbabilityDocument9 pagesChapter 6 - ProbabilityMuhamad Nazrin100% (1)
- The Surprise Attack in Mathematical ProblemsFrom EverandThe Surprise Attack in Mathematical ProblemsRating: 4 out of 5 stars4/5 (1)
- Ansys Element ReferenceDocument1,532 pagesAnsys Element ReferenceOskrRojasNo ratings yet
- Machine VisionDocument50 pagesMachine VisionJayakrishna Kandasamy100% (1)
- Analytical Considerations in The Code Qualification of Piping Systems (U)Document17 pagesAnalytical Considerations in The Code Qualification of Piping Systems (U)Shashank UniyalNo ratings yet
- North Sydney Girls 2009 Year 10 Maths Yearly & SolutionsDocument19 pagesNorth Sydney Girls 2009 Year 10 Maths Yearly & Solutionstechnowiz11100% (2)
- STAB22 FinalExam 2013F PDFDocument23 pagesSTAB22 FinalExam 2013F PDFexamkillerNo ratings yet
- Electronic Expansion ValveDocument5 pagesElectronic Expansion Valveemongclooney11No ratings yet
- Unlocked WIND-BS MethodDocument54 pagesUnlocked WIND-BS MethodAlphyl BalasabasNo ratings yet
- PPT-2 of Chapter 2 Multiplication Rule, Conditional Probability and Bayes TheoremDocument17 pagesPPT-2 of Chapter 2 Multiplication Rule, Conditional Probability and Bayes TheoremDmddldldldlNo ratings yet
- Modul Matematik Tingkatan 4Document9 pagesModul Matematik Tingkatan 4Nur Nadiah100% (1)
- Dew Point & Bubble Point ExcelDocument2 pagesDew Point & Bubble Point Excelayub100% (1)
- Schramm L.L. (Ed.) Surfactants.. Fundamentals and Applications in The Petrolium IndustryDocument630 pagesSchramm L.L. (Ed.) Surfactants.. Fundamentals and Applications in The Petrolium IndustryJaziiel Piineda100% (2)
- QA SLM Math10Q3Mod5 Probability of Union of Two Events Richard C. Romero MergedDocument32 pagesQA SLM Math10Q3Mod5 Probability of Union of Two Events Richard C. Romero MergedRan Haitani100% (1)
- Protein DockingDocument31 pagesProtein DockingFatima IffatNo ratings yet
- Complete Probability in One VideoDocument135 pagesComplete Probability in One VideoGopukrishnan ShajiNo ratings yet
- Math 30-2 Practice Final Exam - 1 - RevisedDocument17 pagesMath 30-2 Practice Final Exam - 1 - RevisedLaura AkamNo ratings yet
- Probability p2Document28 pagesProbability p2Hana ElfarNo ratings yet
- Conditional Probability Lesson 9 of 12: Unit 6Document13 pagesConditional Probability Lesson 9 of 12: Unit 6Jep GatilyoNo ratings yet
- Permutation Example: P (Total 9 Spots) 4/36 1/9Document7 pagesPermutation Example: P (Total 9 Spots) 4/36 1/9राघवतोतलाNo ratings yet
- Maths Class X Sample Paper Test 12 For Board Exam 2024 AnswersDocument16 pagesMaths Class X Sample Paper Test 12 For Board Exam 2024 Answersyash upasaniNo ratings yet
- Addition and Multiplication Laws of Probability: PrerequisitesDocument17 pagesAddition and Multiplication Laws of Probability: PrerequisitespangbattaNo ratings yet
- CBSE Class 10 Mathematics Standard Set 1 30 1 1 Question Paper 2023Document25 pagesCBSE Class 10 Mathematics Standard Set 1 30 1 1 Question Paper 2023sanjaykeerthanartistNo ratings yet
- HW 1 SolnDocument7 pagesHW 1 Solncokeaddict56No ratings yet
- HW 1Document6 pagesHW 1mertozdamarxNo ratings yet
- Introduction To ProbabilityDocument10 pagesIntroduction To ProbabilityDaniel Naoe FestinNo ratings yet
- 40 Questions On Probability For All Aspiring Data ScientistsDocument17 pages40 Questions On Probability For All Aspiring Data ScientistsMas Mentox'sNo ratings yet
- Sample Test 1Document3 pagesSample Test 1BTS LOVERSNo ratings yet
- Summary: Introduction To Probability: Section 1: Introductory Probability Concepts ExperimentDocument12 pagesSummary: Introduction To Probability: Section 1: Introductory Probability Concepts ExperimenthareshtankNo ratings yet
- Review FT Maths S2Document5 pagesReview FT Maths S2rozy kjsNo ratings yet
- Homework 02 SolutionDocument8 pagesHomework 02 Solutionahmadtahirpk100% (1)
- Class 1Document10 pagesClass 1Sandiep SinghNo ratings yet
- 13.conditional Probability, Bayes Theorem Assignment SolutionsDocument11 pages13.conditional Probability, Bayes Theorem Assignment SolutionsGeo TeoNo ratings yet
- Probability p3Document27 pagesProbability p3Hana ElfarNo ratings yet
- Jan 24 Homework Solutions Math 151, Winter 2012 Chapter 3 Problems (Pages 102-110)Document7 pagesJan 24 Homework Solutions Math 151, Winter 2012 Chapter 3 Problems (Pages 102-110)Pei JingNo ratings yet
- HW1 SolutionsDocument4 pagesHW1 SolutionsRey TangNo ratings yet
- Homework #1 - Solution Coverage: Chapter 1-2 Due Date: 18 March, 2021Document3 pagesHomework #1 - Solution Coverage: Chapter 1-2 Due Date: 18 March, 2021estymrtunNo ratings yet
- MR Logbo 6TH MP Examination QuestionsDocument28 pagesMR Logbo 6TH MP Examination QuestionskolawoleNo ratings yet
- YT +Probability+-+12th+EliteDocument191 pagesYT +Probability+-+12th+EliteKhairuljewel AlamNo ratings yet
- 505 Review Problems For Final SolutionsDocument6 pages505 Review Problems For Final SolutionsGabe GuerrierNo ratings yet
- Probability: Before You StartDocument32 pagesProbability: Before You StartSuhaila EhabNo ratings yet
- Maths 2A Probability Important QuestionsDocument4 pagesMaths 2A Probability Important Questionssimhadri.sridharNo ratings yet
- Ch8 Review3Document17 pagesCh8 Review3Dana Al-WakilNo ratings yet
- WorksheetsDocument35 pagesWorksheetsWasif ImranNo ratings yet
- Principles of Math 12 - Probability Practice Exam PDFDocument19 pagesPrinciples of Math 12 - Probability Practice Exam PDFJasgeoNo ratings yet
- Principles of Math 12 - Logarithms Practice ExamDocument18 pagesPrinciples of Math 12 - Logarithms Practice ExamArnab ChakrabartiNo ratings yet
- Mathematics W18Document31 pagesMathematics W18Alexander IkechukwuNo ratings yet
- Some Solved Math Test Quetions With ReferencesDocument14 pagesSome Solved Math Test Quetions With ReferencesGhulam FareedNo ratings yet
- Maths Class X Sample Paper Test 13 For Board Exam 2024 AnswersDocument16 pagesMaths Class X Sample Paper Test 13 For Board Exam 2024 Answersyash upasaniNo ratings yet
- Statistics Homework Sample 3Document8 pagesStatistics Homework Sample 3Jack ClarkNo ratings yet
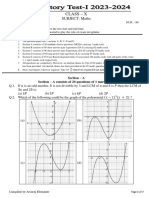
- Class-X - Preparatory Test I 2023-24 1.0Document7 pagesClass-X - Preparatory Test I 2023-24 1.0Nirmala DeviNo ratings yet
- Đề Thi K48 TrướcDocument3 pagesĐề Thi K48 TrướcTrần Khánh LinhNo ratings yet
- STA 5325 HW 1 Ramin ShamshiriDocument13 pagesSTA 5325 HW 1 Ramin ShamshiriRedmond R. Shamshiri100% (2)
- 2.3 Conditional ProbabilityDocument3 pages2.3 Conditional ProbabilityKumar Gaurab JhaNo ratings yet
- Maths Class X Sample Paper Test 14 For Board Exam 2024 AnswersDocument14 pagesMaths Class X Sample Paper Test 14 For Board Exam 2024 AnswersLoki GANo ratings yet
- Psat NMSQT Practice Test 1 Explanations 54 93Document40 pagesPsat NMSQT Practice Test 1 Explanations 54 93api-395493982No ratings yet
- Tutorial 4 NGUYEN Thanh SonDocument2 pagesTutorial 4 NGUYEN Thanh SonThanh Sơn NguyễnNo ratings yet
- EST II - Math Level 1 - May 2021Document14 pagesEST II - Math Level 1 - May 2021Hazem ShehabNo ratings yet
- Chapter 6 II Math Reasoning Enhance - EditDocument28 pagesChapter 6 II Math Reasoning Enhance - EditTanYeeTingNo ratings yet
- Chapter 9 - Chapter TestDocument13 pagesChapter 9 - Chapter Testshwampa0% (1)
- Pre Board Sample 2Document6 pagesPre Board Sample 2manojgoyaljuly8No ratings yet
- Conditional Probability and Bayes' TheoremDocument9 pagesConditional Probability and Bayes' TheoremAlisha GarciaNo ratings yet
- This Test Contains A Total of 10 Objective Type Questions. Each Question Carries 1 Mark. There Is NO NEGATIVE MarkingDocument13 pagesThis Test Contains A Total of 10 Objective Type Questions. Each Question Carries 1 Mark. There Is NO NEGATIVE Markingvarunkohliin100% (1)
- BTests 1 To 9 2021Document233 pagesBTests 1 To 9 2021Pravar Garg100% (1)
- Probability: Counting TechniquesDocument54 pagesProbability: Counting Techniquesمحمد بركاتNo ratings yet
- JBMO 2012 Problems SolutionDocument5 pagesJBMO 2012 Problems SolutionjfmarquesNo ratings yet
- Krabi 22-23Document1 pageKrabi 22-23Shashank UniyalNo ratings yet
- Modern Flange Design - Taylor Forge Engineered ProductsDocument52 pagesModern Flange Design - Taylor Forge Engineered ProductsShashank UniyalNo ratings yet
- A. KAPP-3&4/RAPP-7&8:: Monthly Performance ReportDocument2 pagesA. KAPP-3&4/RAPP-7&8:: Monthly Performance ReportShashank UniyalNo ratings yet
- Comparison of Rock Soil and Soft Soil SpectraDocument2 pagesComparison of Rock Soil and Soft Soil SpectraShashank UniyalNo ratings yet
- Description of Crane ValveDocument8 pagesDescription of Crane ValveShashank UniyalNo ratings yet
- Chapter4 97Document13 pagesChapter4 97Shashank UniyalNo ratings yet
- Experimental Determination of Resultant Roll Force at Hot Plate Mill 5000 O.A. GasiyarovaDocument4 pagesExperimental Determination of Resultant Roll Force at Hot Plate Mill 5000 O.A. GasiyarovaSamir BoseNo ratings yet
- GDTNTDocument96 pagesGDTNTSharath Thimmegowda100% (1)
- Physical Science With Earth ScienceDocument26 pagesPhysical Science With Earth ScienceAljenneth MicallerNo ratings yet
- Chapter 1 - Introduction and Basic ConceptsDocument8 pagesChapter 1 - Introduction and Basic ConceptsYeevön LeeNo ratings yet
- Paper1 IntegrationDocument11 pagesPaper1 IntegrationParidah YaacobNo ratings yet
- Calculo Del Tamaño Del AcumuladorDocument1 pageCalculo Del Tamaño Del AcumuladorJUAN JOSE VESGA RUEDANo ratings yet
- Vlasov Computation of Prismatic SHellsDocument53 pagesVlasov Computation of Prismatic SHellsMaliOdKužineNo ratings yet
- Numerical Methods For Engineers 6th Edition Solution ManualDocument4 pagesNumerical Methods For Engineers 6th Edition Solution Manualঅর্পিতা রহমান অথৈNo ratings yet
- Channel Code - For DWDM Channel JD PDFDocument2 pagesChannel Code - For DWDM Channel JD PDFovc_etnNo ratings yet
- STAAD - Pro Syllabus 1Document3 pagesSTAAD - Pro Syllabus 1Anukool kumarNo ratings yet
- Boyle's Law Computer ActivityDocument3 pagesBoyle's Law Computer ActivityAnonymous 52Z8ZFkv0% (1)
- Kinematics of A Particle AllDocument160 pagesKinematics of A Particle AllaychiluhimhailuNo ratings yet
- 1997 Podlubny FO PIDDocument6 pages1997 Podlubny FO PIDfidelpaxoNo ratings yet
- Chapter 5 FourierDocument85 pagesChapter 5 Fourieryug varshneyNo ratings yet
- Carbonato de Glicerina PDFDocument29 pagesCarbonato de Glicerina PDFbexigaobrotherNo ratings yet
- NilsonDocument15 pagesNilsonJefferson FelipeNo ratings yet
- Pipeting and Dilution Lab: Biochemistry Laboratory Experiment No. 1Document12 pagesPipeting and Dilution Lab: Biochemistry Laboratory Experiment No. 1Adellaine Lois GreyNo ratings yet
- Gas Laws NOTESDocument2 pagesGas Laws NOTESKimberly MutangaNo ratings yet
- PVC Plasticizers VFDocument11 pagesPVC Plasticizers VFengrasrarNo ratings yet
- Frequency Response EEE 101 C 2003 M.C. Ramos UP EEE DepartmentDocument22 pagesFrequency Response EEE 101 C 2003 M.C. Ramos UP EEE DepartmentPao YapNo ratings yet