UNIDAD 5

Series de Fourier

5.1 Funciones ortogonales, conjuntos ortogonales y conjuntos ortonormales

Se dice que dos funciones f1 ( x ) y f 2 ( x ) son ortogonales en el intervalo a < x < b si cumplen con:
b
∫ f ( x ) f ( x ) dx = 0
a 1 2

Esta idea se hace extensiva a un conjunto de n funciones, donde se dice que el conjunto es ortogonal si
cualquier par de funciones del conjunto es ortogonal, es decir:
b
∫ f ( x ) f ( x ) dx = 0
a i j para cualquier i y j diferentes

La norma cuadrada de una función en el intervalo a < x < b está definida como:
2 b 2
f ( x ) ≡ ∫  f ( x )  dx
a

A su vez, la norma de una función es la raíz cuadrada de la norma cuadrada:

b 2
f ( x) = ∫  f ( x )  dx
a

Se dice que un conjunto de funciones es ortonormal si es ortogonal y además la norma de cada una de las
funciones es igual a 1. Cualquier conjunto ortogonal de funciones se puede convertir en ortonormal si se
divide cada función entre su norma.

5.2 Definición de serie de Fourier

El conjunto de funciones 1 , cos x , cos 2x , cos 3x , …, cos nx , …, sen x , sen 2x , sen 3x , …, sen nx , …,
es ortogonal en el intervalo −π ≤ x ≤ π . Si f ( x ) es una función definida en el intervalo −π ≤ x ≤ π ,
entonces se puede representar como una serie trigonométrica infinita de la forma:

a0 ∞
f ( x) = + ∑ ( an cos nx + bn sen nx )
2 n =1
que se denomina serie de Fourier de f ( x ) , donde a0 , an y bn son coeficientes obtenidos mediante la
propiedad de ortogonalidad, y se calculan de la siguiente forma:

1 π 1 π 1 π
f ( x ) dx f ( x ) cos nxdx f ( x ) sen nxdx
π ∫−π π ∫−π π ∫−π
a0 = an = bn =

La serie de Fourier es una función periódica con periodo p = 2π .

5.3 Convergencia de una serie de Fourier

Teorema de convergencia: Sean f ( x ) y su derivada f ′ ( x ) continuas parte por parte en el intervalo
−π ≤ x ≤ π , es decir que f ( x ) y f ′ ( x ) sean continuas en el intervalo excepto en un número finito de
puntos en los que tengan discontinuidades finitas. Entonces:

REVISIÓN 1 – 64068.45 Página 5-1

 UNIDAD 5
SERIES DE FOURIER

(A) en un punto de continuidad, la serie de Fourier converge a f ( x ) .

(B) en un punto de discontinuidad, la serie de Fourier converge a 1  f ( x + ) + f ( x − )  , donde f ( x + ) y
2  
f ( x − ) representan los límites de la función por la derecha y por la izquierda, respectivamente.

5.4 Serie de Fourier de una función de periodo arbitrario

Mediante un cambio de variables, se puede generalizar una serie de Fourier para una función definida en
cualquier intervalo arbitrario centrado en el origen, normalmente − L ≤ x ≤ L . La serie de Fourier se vuelve:

a0 ∞  nπx nπx 
f ( x) = + ∑  an cos + bn sen 
2 n =1  L L 
y los coeficientes de determinan con las siguientes relaciones:

1 L 1 L nπx 1 L nπx
f ( x ) dx f ( x ) cos f ( x ) sen
L ∫− L ∫ ∫
a0 = an = dx bn = dx
L − L L L − L L

5.5 Serie de Fourier de funciones pares e impares

Una función es par si f ( − x ) =f ( x) . Una función es impar si f ( − x ) =− f ( x) .

Al multiplicar funciones pares o impares se observan las siguientes reglas:

par × par = par impar × impar = par par × impar = impar

[
Al integrar una función par o impar en un intervalo − L, L , el resultado es: ]
L L L
∫ f ( x ) dx = 2 ∫ f ( x ) dx si f ( x ) es par ∫ f ( x ) dx = 0 si f ( x ) es impar
−L 0 −L

Tomando en cuenta que la función seno es impar y la función coseno es par, y empleando estas propiedades
de las funciones pares e impares, se encuentra que para una función par bn = 0 y para una función impar
a0 = 0 y an = 0 , por lo que se puede emplear las siguientes formas simplificadas de la serie de Fourier:

FUNCIÓN SERIE COEFICIENTES

Par a0 ∞ nπx 2 L 2 L nπx

f ( x=
) + ∑ an cos f ( x ) dx f ( x ) cos
L ∫0 ∫
a0 = an = dx
2 n =1 L L 0 L

Impar ∞
nπx 2 L nπx
f ( x ) = ∑ bn sen bn = ∫ f ( x ) sen dx
n =1 L L 0 L

REVISIÓN 1 – 64068.45 Página 5-2

 UNIDAD 5
SERIES DE FOURIER

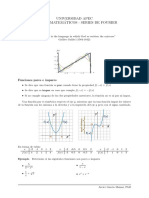
5.6 Series de Fourier de medio intervalo

Considérese ahora una función definida solamente en el intervalo 0 < x < L como la
mostrada a la derecha. Ya que la serie de Fourier es una función periódica definida
formalmente en − L < x < L , se está en libertad de asumir cuál es el comportamiento de
la serie para el intervalo − L < x < 0 . Existen tres posibilidades: asumir que la función es
par, asumir que es impar, o asumir que es periódica.

5.6.1 Extensión par (serie de cosenos)

función original definida extensión par en el serie de Fourier resultante

en 0 < x < L intervalo − L < x < 0

La serie de Fourier se obtiene entonces empleando las mismas fórmulas que para una función par:

EXTENSIÓN SERIE COEFICIENTES

Par a0 ∞ nπx 2 L 2 L nπx

f ( x=
) + ∑ an cos f ( x ) dx f ( x ) cos
L ∫0 ∫
a0 = an = dx
2 n =1 L L 0 L

5.6.2 Extensión impar (serie de senos)

función original definida extensión impar en el serie de Fourier resultante

en 0 < x < L intervalo − L < x < 0

La serie de Fourier se obtiene entonces empleando las mismas fórmulas que para una función impar:

EXTENSIÓN SERIE COEFICIENTES

Impar ∞
nπx 2 L nπx
f ( x ) = ∑ bn sen bn = ∫ f ( x ) sen dx
n =1 L L 0 L

REVISIÓN 1 – 64068.45 Página 5-3

 UNIDAD 5
SERIES DE FOURIER

5.6.3 Extensión periódica (serie de Fourier)

función original definida extensión par en el serie de Fourier resultante

en 0 < x < L intervalo − L < x < 0

En este caso, la serie de Fourier tiene periodo p = L y está dada por:

EXTENSIÓN SERIE COEFICIENTES

Periódica a0 ∞  nπx nπx  2 L

f ( x) = + ∑  an cos f ( x ) dx
L ∫0
+ bn sen  a0 =
2 n =1  L/2 L/2
2 L nπx
an = ∫ f ( x ) cos dx
L 0 L/2
2 L nπx
bn = ∫ f ( x ) sen dx
L 0 L/2

5.7 Forma compleja de la serie de Fourier

Una función definida en el intervalo − L < x < L puede expresarse también como una sumatoria de
funciones exponenciales de números complejos de la forma:
∞
f ( x) = ∑ce
n = −∞
n
nω0 xi

donde cn son los coeficientes complejos de la serie de Fourier, que es periódica con periodo p = 2L , y
ω0 es la frecuencia fundamental dada por:
2π π
ω0= =
p L
La forma compleja de la serie de Fourier resulta más conveniente que la forma trigonométrica para el
análisis de ciertos problemas de ingeniería. Sin embargo, debe tenerse en cuenta los siguientes dos puntos:
 El coeficiente c0 , correspondiente al valor n = 0 , no siempre se puede obtener de la fórmula
general para los demás coeficientes cn .
 Al llevar a cabo la sumatoria, siempre debe tomarse el mismo número de términos para valores
positivos y negativos de n .
Por esta razón, la serie compleja de Fourier se suele representar mejor en la forma:
∞

(
c0 + ∑ cn e nω0 xi + c− n e − nω0 xi
f ( x) = )
n =1

REVISIÓN 1 – 64068.45 Página 5-4

 UNIDAD 5
SERIES DE FOURIER

donde los coeficientes están dados por:

1 L 1 L
f ( x ) dx f ( x ) e − nω0 xi dx
2 L ∫− L ∫
c0 = cn = c− n = cn (complejo conjugado)
2L − L

Mediante la fórmula de Euler, puede demostrarse la relación de los coeficientes de la serie compleja de
Fourier con la serie trigonométrica de Fourier:

c0 = 12 a0 cn
= 1
2 ( an − bni ) c− n
= 1
2 ( an + bni )
5.8 Forma harmónica de la serie de Fourier
Empleando identidades, la serie trigonométrica de Fourier se puede escribir también en la forma harmónica:

a0 ∞  nπx 
f ( x=
) + ∑ d n cos  + δn 
2 n =1  L 
donde a0 es el mismo coeficiente de la serie trigonométrica y:

 b 
dn
= an2 + bn2 δn arctan  − n 
=
 an 

REVISIÓN 1 – 64068.45 Página 5-5