Professional Documents
Culture Documents
Trachtenberg System - Wikipedia
Trachtenberg System - Wikipedia
Uploaded by
AliceAlormenu0 ratings0% found this document useful (0 votes)
65 views9 pagesTrachtenberg
Copyright
© © All Rights Reserved
Available Formats
PDF or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentTrachtenberg
Copyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
0 ratings0% found this document useful (0 votes)
65 views9 pagesTrachtenberg System - Wikipedia
Trachtenberg System - Wikipedia
Uploaded by
AliceAlormenuTrachtenberg
Copyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
You are on page 1of 9
ra07 Trachtenberg system - Wikipedia
Trachtenberg system
From Wikipedia, the free encyclopedia
The Trachtenberg system is a system of rapid mental calculation, The system consists of a number of readily
‘memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the
Russian Jewish engineer Jakow Trachtenberg in order to keep his mind occupied while being held in a Nazi
concentration camp.
The rest of this article presents some methods devised by Trachtenberg. The most important algorithms are the
ones for general multiplication, division and addition. Also, the Trachtenberg system includes some specialized
methods for multiplying small numbers between 5 and 13.
The chapter on addition demonstrates an effective method of checking calculations that can also be applied to
multiplication.
Contents
= 1 General multiplication
= 2 General addition
= 3 Other multiplication algorithms
= 3.1 Multiplying by 11
= 3.2 Multiplying by 12
= 3.3 Multiplying by 6
= 3.4 Multiplying by 7
= 3.5 Multiplying by 9
Multiplying by 9 Hejea method
Multiplying by 8
Multiplying by 4
Multiplying by 3
= 3.10 Multiplying by 5
= 3.11 Multiplying by 2
Publications
In popular culture
Other systems
Software
References
External links
General multiplication
The method for general multiplication is a method to achieve multiplications a x b with low space complexity,
i.e. as few temporary results as possible to be kept in memory. This is achieved by noting that the final digit is
completely determined by multiplying the last digit of the multiplicands, This is held as a temporary result. To
find the next to last digit, we need everything that influences this digit: The temporary result, the last digit of a
times the next-to-last digit of b, as well as the next-to-last digit of a times the last digit of b. This calculation is
performed, and we have a temporary result that is correct in the final two digits.
In general, for each position n in the final result, we sum for all é
a (digit at) x b (digit at (n — 4).
hitps:ifen wkipedia.orgwikiTracntenberg_ system 19
ra07 Trachtenberg system - Wikipedia
People can learn this algorithm and thus multiply four digit numbers in their head — writing down only the final
result. They would write it out starting with the rightmost digit and finishing with the leftmost.
Trachtenberg defined this algorithm with a kind of pairwise multiplication where two digits are multiplied by
one digit, essentially only keeping the middle digit of the result, By performing the above algorithm with this
pairwise multiplication, even fewer temporary results need to be held.
Example: 123456 x 789
To find the first digit of the answer, start at the first digit of the multiplicand:
The units digit of 9 x 6
The first digit of the answer is 4
To find the second digit of the answer, start at the second digit of the multiplicand:
The units digit of 9 x 5 plus the tens digit of 9 x 6 plus,
The units digit of 8 x 6.
5+548=18
The second digit of the answer is 8 and carry 1 to the third digit.
To find the third digit of the answer, start at the third digit of the multiplicand:
The units digit of 9 x 4 plus the tens digit of 9 x 5 plus
The units digit of 8 x 5 plus the tens digit of 8 x 6 plus
The units digit of 7 x 6
6+4+0+4+2=16+1 carried from the second digit.
The third digit of the answer is 7 and carry 1 to the next digit.
bps:en wikipedia ori Traentenberg_system
219
ra07 Trachtenberg system - Wikipedia
To find the fourth digit of the answer, start at the fourth digit of the multiplicand:
The units digit of 9 x 3 plus the tens digit of 9 x 4 plus,
The units digit of 8 x 4 plus the tens digit of 8 x 5 plus,
The units digit of 7 x 5 plus the tens digit of 7 x 6.
TH34+24+44+5+4= 2541 carried from the third digit,
The fourth digit of the answer is 6 and carry 2 to the next digit
Trachtenberg called this the 2 Finger Method. The calculations for
finding the fourth digit from the example above are illustrated at right.
The arrow from the nine will always point to the digit of the AE 11
multiplicand directly above the digit of the answer you wish to find, 123456 x 789
with the other arrows each pointing one digit to the right, Each arrow se
head points to a UT Pair, or Product Pair. The vertical arrow points to _784
the product where we will get the Units digit, and the sloping arrow
points to the product where we will get the Tens digits of the Product,
Pair. If an arrow points to a space with no digit there is no calculation
for that arrow. As you solve for each digit you will move each of the arrows over the multiplicand one digit to
the left until all of the arrows point to prefixed zeros.
2 Finger method
Division in the Trachtenberg System is done much the same as in
multiplication but with subtraction instead of addition. Splitting the
idend into smaller Partial Dividends, then dividing this Partial
Dividend by only the left-most digit of the divisor will provide the
answer one digit at a time. As you solve each digit of the answer you
then subtract Product Pairs (UT pairs) and also NT pairs (Number-Tens)
from the Partial Dividend to find the next Partial Dividend. The Product
Pairs are found between the digits of the answer so far and the divisor. Setting up for Division
Ifa subtraction results in a negative number you have to back up one
digit and reduce that digit of the answer by one. With enough practice this method can be done in your head.
General addition
‘A method of adding columns of numbers and accurately checking the result without repeating the first
operation. An intermediate sum, in the form of two rows of digits, is produced. The answer is obtained by
taking the sum of the intermediate results with an L-shaped algorithm, As a final step, the checking method that
is advocated removes both the risk of repeating any original errors and allows the precise column in which an
error occurs to be identified at once. It is based on a check (or digit) sums, such as the nines-remainder method.
For the procedure to be effective, the different operations used in each stage must be kept distinct, otherwise
there is a risk of interference.
hitps:ifen wkipedia.orgwikiTracntenberg_ system a9
You might also like
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- ISB, IsBe Engine Troubleshooting and Repair Manual 3.9, QSB4.5QSB5.9, QSB6.7, IsC, QSC8.3, IsL, IsLe 9 and QSL9, CM850 Volume 3Document1,048 pagesISB, IsBe Engine Troubleshooting and Repair Manual 3.9, QSB4.5QSB5.9, QSB6.7, IsC, QSC8.3, IsL, IsLe 9 and QSL9, CM850 Volume 3AliceAlormenu88% (17)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- OscillationDocument6 pagesOscillationAliceAlormenuNo ratings yet
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- PID ControllerDocument24 pagesPID ControllerAliceAlormenuNo ratings yet
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- Ewe LanguageDocument5 pagesEwe LanguageAliceAlormenuNo ratings yet
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5810)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (844)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- Gauss's LawDocument10 pagesGauss's LawAliceAlormenuNo ratings yet
- Structural Health MonitoringDocument10 pagesStructural Health MonitoringAliceAlormenuNo ratings yet
- Singularity (Mathematics)Document4 pagesSingularity (Mathematics)AliceAlormenuNo ratings yet
- Drill StringDocument5 pagesDrill StringAliceAlormenuNo ratings yet
- Quantum SuperpositionDocument14 pagesQuantum SuperpositionAliceAlormenuNo ratings yet
- Control EngineeringDocument5 pagesControl EngineeringAliceAlormenuNo ratings yet
- Orbital ManeuverDocument6 pagesOrbital ManeuverAliceAlormenuNo ratings yet
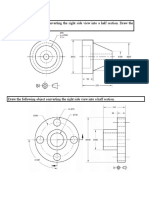
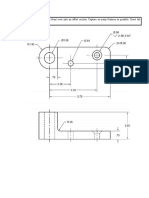
- Draw The Following Object Converting The Right Side View Into A Half Section. Draw The Appropriate Cutting Plane LineDocument2 pagesDraw The Following Object Converting The Right Side View Into A Half Section. Draw The Appropriate Cutting Plane LineAliceAlormenuNo ratings yet
- Worked Example.: Velocity and Acceleration (Including Coriolis Component) in MechanismsDocument4 pagesWorked Example.: Velocity and Acceleration (Including Coriolis Component) in MechanismsAliceAlormenuNo ratings yet
- Section ViewDocument1 pageSection ViewAliceAlormenuNo ratings yet
- Ultra High Molecular Weight PolyethyleneDocument7 pagesUltra High Molecular Weight PolyethyleneAliceAlormenuNo ratings yet
- Carbon Fiber Reinforced PolymerDocument10 pagesCarbon Fiber Reinforced PolymerAliceAlormenuNo ratings yet
- Soft Robotics Is The Specific Subfield ofDocument7 pagesSoft Robotics Is The Specific Subfield ofAliceAlormenuNo ratings yet
- Snake Arm RobotDocument3 pagesSnake Arm RobotAliceAlormenuNo ratings yet
- Rag Joint: See AlsoDocument1 pageRag Joint: See AlsoAliceAlormenuNo ratings yet