SOCIETY OF PETROLEUM ENGINEERS OF AINE PAPER 6200 North Central Expressway mozer SPE 4529 Dallas, Texas 75206 THIS 15 A PREPRINT --- SUBJECT TO CORRECTLON The |sochronal Testing of Oi! Wells By Retkovich, Member AIME, Phillips Petroleum Co. © Copyright 1973 American Institute of Mining, Metallurgical, and Petroleum Engineers Inc. Tals paper vas prepared for the 48th Annual Fall Meeting of the Society of Petroleum Engineers of AIME, to be held in Las Vegas, Nev., Sept. 30-Oct, 3, 1973. Permission to copy is restricted to an abstract of not more than 300 words. ‘Illustrations aay not be copied. The abstract. should contain conspicuous acknowledguent of where and by vhon the paper is presented, Publication eleevhere after publication in the JOURNAL OP PETROLEUM TECHNOLOGY or the SOCIETY OF PEOROLEIM ENGINEERS JOURNAL io usually granted upon request to the Sditor of the appropriate journal provided agreesent to give proper credit is nade. Discussion of this paper is invited, Three copies of any discussion should be sent to the Society of Petroleum Engineers office. Such discussion may be presented at the above meeting and, with the paper, say be considered for publication in one of the two SPE magazines. ‘ABSTRAGT ourves. ‘This paper presents the results and methods of analyzing scchronal and flow after flow multipoint back-pressure tests conducted on of] wells. Tests were conducted in reser yoirs with permeabilities ranging from 6 MD to > 1000 MD, Reservoirs in which oi} well multipoint back-pressure tests were obtained ranged from highly undersaturated, to saturated at initial reservoir pressure, to a partially depleted field with a gas saturation existing above the oritical. Each of these three reservoir fluid states can result in different interpretation methods. Back-pressure tests were run to pseudo-steady state in the field where the saturation was above the critical gas saturation. In all cases, ofl well back-pressure curves were found to follow the sane general form as that used to express the rate-pressure relationship of a gas well 997 55 gt = Bye From some 40 ofl well back-pressure tests examined, the exponent n was found to lie between 0,568 and 1.000, very near the linits commonly accepted for gas well bazk-ressure 2yn References and illustrations at end of paper, Flow point alignnent to establish an ofl weil back~presgure curve on the customary log q, vs. log 4(p*) plot is considered to be as ‘aa that obtained on gas well back- Pressure tests, ‘This paper denonstrates that gas wells and of wells behave very similarly and should be tested and anslyzed using the same basic flow equations. INTRODUCTION Multipoint back-pressure testing of gas wells dean accepted procedure for establishing gaz well's performance curve, Flow after flow! and Aeochronal? testing are the two basic methods commonly used, In high permeability reservoirs, either method ean be employed. In low per- mesbility reservoirs, the Isochronal method of testing eliminates the transient effects that can severely distort the results obtained from a flow after flow test. Methods for analyzing and caloulating gas well performance curves have been the subject of numerous investigations, The bulk of these Anvestigations have examined non—Darey flow behavior, the primary reason that multipoint tests are conducted. Multipoint testing of ofl wells is not now wrrent practice. As early as 1930, however,2 ‘THE ISOCHRONAL TESTING OF OIL WELLS SFE 4529 1. V. Moore? reported the results of an ofl Well” mitipoint test conducted on the Humble Smith 4-2 in the Yates Field. The purpose of the back-pressure test vas to demonstrate a method of establishing a well's open flow potential without produeing the well wide open. ‘The need for establishing an accurate performance curve for an oil well 4s as Amportant as deteraining one for a gas well. In the search for nev oil, the industry is turn ing to remote areas such as the Arctic and offshore. Critical questions of whether to develop, and if 20, how to develop a field hinge on the ability to accurately predict 2 well's deliverability. Often, because of equipment limitations, the rates of production obtained during drillstem testing are much less ‘than those planned for full development. ‘The traditional method for predicting production rates and drawdowns for oil wells has been based on the concept of the productiv- Aty index (PI), which has been used in the oil. industry for many years. The usual form of ‘the equation Goo Pp yee ee @ is valid only for systems producing an ideal homogeneous liquid obeying Uaroy's lav. This condition normally holds for oi] wells when the ofl is undersaturated throughout the produeing formation. It has long been recognized that in reservoirs existing at or below the bubble- point pressure, producing wells do not follow this simple equation, Actual field tests indicate that oll flow rates obtained at increasing drawdowns decline much faster than would be predicted by Bq. 1. Evinger and Muskat* first derived a theoretical productivity index for steady state radial flow in an attempt to account for the observed non-linear flow behavior of oil vells and arrived at the following equation Pe 8h Be r, [ f(p) dp. . « (2) (8) ae wnere £ (p) = yy Galewlations using #3. 2 based on typical reservoir and fluid properties indicated that PL at a fixed reservoir pressure Pe (as defined from Eq, 1) decreases with increasing drawdown. In a computer study by Vogel”, results boned on tro-phase flow theory were presented to indicate that a single empirical inflow performance relationship (IPR) equation might be valid for most solution-gas drive reservoirs, He found that @ single dimensionless IF equation| approximately held for several hypothetical solution-gas drive reservoirs even when using a wide range of oil FVT properties and reservoir relative permeability curves, The fact that his study covered a wide range of fluid properties and relative permeability curves to obtain a single reference ourve, can not be over emphasized. Vogel then proposed that his equation be used to take the place of the linear productivity index relationship for solution- gas drive reservoirs when the reservoir pressure is at or below the bubble-oint pressure, ‘The proposed empirical reference equation (IPR) dn dimensionless form was given as Se = 00 (Bo Qa ‘A comparison was made of IPR's for liquid flow, gas flow (n=l) and two-phase flow (his reference curve) on a dimensionless basis, (Fig. 1). As is evident from Fig. 1 the position of the two-phase reference curve relative to liquid and gas flow indicates that ofl wells producing as if in a solution-gas drive reservoir should actyally jehave more like a gas well, i.e., (Fp? pe) v8~ should plot as @ straight Line on log-lof paper with a slope (n) near unity. « 3) This paper prevents the results of multi- point backpressure tests taken ata single Feservoir pressure level (fy). These results Show that the perfornance elves for an ofl well San be expressed by a nore general end faniliar equation Sinilar £9 that used for gas Wells, 2 9g 9S (Bg? = Pye a) Reservoire in which oi well multipoint backpressure teste were obtained ranged from highly undersaturated, to saturated at initial Teservoir pressure, to a partially depleted Teld with a gas saturation existing above the critical (equilibrium) gas saturation. Equation k was found to be valid for tests conducted in all three reservoir fluid states, even for the conditions where flowing pressures were vel) above the bubble-point pressure, Permesbilities Of the reservoirs ranged fron 6 to >1000 rillidareys. Flow point allgntent to establish an oil well. back-pyeesure ourve on the customary Jog a, vs. log 4(p) was found to be as good as that Sbtained on gas well back-pressure tests, BASIC EQUATIONS AND PRESSURE FUNOTTONS The basic flow equation given by Svinger and Muskat# for steady-state flow, applicable to either oil or gas flow, isM, J, FeTKOVIGH 3 f(p)ap. 2. (@) where f (p) can be any function of pressure. 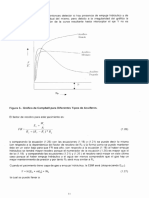Using the typical pressure function depicted in Fig, 2 4¢ 4s obvious that we can evaluate ‘the total integral in two parts and write ag seit [PH Wyal59) ap fas (i) += Ys Fo ~ if p *f So al... Yo Bo For flow in the region where the pressures are above the bubble point pressure if we assume k= 1 ( neglecting the pressure dependent permeability term for simplicity of presentation only) and treat (u.B,) evaluated at the average pressure (p,tn,)/2 fe°can write a, = nei Kye (SP) ap cea eee ee eH) Except for the addition of the necessary skin torm,s' (discussed later in the paper) Ea. 6 is ddentioal to that derived by Handy2l, Figure 2 illustrates a plot of 1/u,B, as a function of pressure for an undersaturated oil reservoir. Also, dravn on this figure is a dashed line representing the effect of relative permeability (k_.) on drawdowns below the bubble-point préoure, It is assuned for purposes of denonstration that k_/(u,B)) is Linear and its intercept is 0 at" présfure. ‘The simplifying assumption of the 0 intercept for sag igh) somrentaataly dottnne Vogel's TH cbfve nd exactly defines Eq. 4 when n=l.) Also,| Gran on Fig. 2 49a hypothetical pressure function k,,/(u,B,) represented as a constant for all préSsurfs? It is clear that a constant value of k__/(3,8,) over the entire Fressure drawdown rifge fe°required to obtain a constant productivity index (PI). Figure 3 illustrates plots of 1/(u,B,) for two high pressure gas reservoirs. Ci ‘A was obtained from caloulations using the reservoir gas analysis and standard correlations of Z and u, as functions of critical pressure and ten- ature, Curve B was obtained directly from a PVT study, One striking feature of curve A is ‘the fact that 1t resembles that of an under- saturated ofl reservoir with an apparent or pseudo bubble-foint pressure near 2500 psia, ‘the normal inflestion point of a 2 curve. A further observation that can be made from curves A and B is that a region exists where a gas well can be considered to behave as a Liquid, i.e., 1/(u,B,) 4s nearly constant or only slightly chanfifig with pressure as is the case for the pressure function of an undersaturated ofl reservoir above the bubble- point pressure, For the region where the pressure funstion is a constant, or nearly s0, we can innediately write upon integration of Eq. 2 the well known steady-state single phase flow equation: (Py ~ Fue) b=(=2)+4] Seas ease eee Si ee B in Fig. 3 over a considerable range of ee siete a portional to Sp insteal of O(p). This, in Hare po. Now considering the entire pressure function from p, to 0, for either the oil or gas curves, (the dfshed line in Fig. 2) we note that £ (p) ean be represented approximately by two sepa~ rate straight line segments. The approximate flow equation then, over the total pressure interval, can be written as: (See Appendix) 1.08 ih an (22 ‘ja [ (4 Pere . [Pre (Ry?) + cn. @) — @= 9" Om? ~ By?) +5 (egw) > -C8N) a or For draxdowns both above and below the bubble-point pressure, a backpressure curve plot will appear as two line segnents, with the intersection yielding an approximate value for the reservoir bubble-point pressure. This then offers an approach for determining a reservoir's bubble-point pressure from an isochronal test. For an isochronal test, @ constant reservoir radius of investigation is obtained for each flow-an insitu constant volume ell, If the degree of undersaturation 4s slight, the tvo line seguents may not be definable. Unstable flow conditions in the tubing at the4 THE ISOCHRONAL TESTING OF OIL WELIS SPE 4529 low flow rates necessary to define the single~ phase flow conditions may preclude defining two straight lines, Further, as will be denon- strated later, non-Darcy flow can exist even when all flowing pressures are above the bubble- point pressure. Conceivably then this could Yead to even three Mine segnents. For the case of all drawdowns below the bubble-point pressure J(pe - p,) 1s a constant, while the reaaining term varies non-linearly with flowing pressure, ryr- The composite effect results in an equation of the form 930 (P= Bye)” 9) decreases to the pressure py, n> 1.0 and c-> 3? such that for the ofl well case, only the two-phase flow tern renains. We thus obtain| the basie equation suggested fron Vogel's results for py < mE AaB, ~ (0) A significant conclusion to be drawn from Eq. 9 4s that a gas well or an ofl well can havea slope less than 1,0 on a log q vs. log a(p*) plot without non-Darey flow existing. ‘The slope (n) in this case is strictly a result of the shape of the wells pressure function. This possibility, for a gas well, was recognized and reported by Howan and Clegg °. Bq. 10 mst be further generalized with an exponent (n) in light of results obtained from multipoint back-pressure tests conducted on ofl wells for both single-phase and two- phase flow to a = 9) (Pg? = ye Pee ee GD Bq, 11 4s Adentical in form to the gas well back-pressure equation. For constant rate transtent gas flow, the gas well bogk-preseure equation 4s usually expressed by 78, 7.08 to (Pg = Pp) a TS kt in ¥ z Blue, sry’ + at Dg + 42) Other than for the unique fluid property cases discussed above, or a pressure dependent per- meability effect, the non-Darey flow term in Hq. 12 is required to obtain an exponent (n) less than 1.0, 9 In terns of a pseudo-pressure? m(p) 08 kh fa(p,) - ale] 2 «+ 3) where m (p) can also in a pressure Uopondent permsentaity (Orit Ko (SP) P m (p) = Sf us (the effect of a pressure dependent permeability could readily be displayed in Figs. 2 and 3.) (S,p) dp. - (14) Equation 12 or 13 then should be appli- cable for analyzing both ofl well and gas well back-pressure tests. RATE AND TIME DEPENDENT SKIN, = (a Slopes much less than 1 were consistently obtained from isochronal teats conducted en oil wells in saturated reservoire, for under- saturated reservoirs, the shape of the preasure function was shown to be cspatle of accounting for slopes leas than 1. Since Vogel's. work ‘based of tworghase flow theory Indloaved back pressure curve slopas should be unity or even eater, 4 near well bore effect wan’ suspected, Ll of Vogel's results show the first calculated IPR curve after 0.1% of original oil-in-place Le recovered. The effect of intial gua eat~ tration bulld-up around the wellbore may ng have been present in his results.) Hai studied the adverse effect on PI of two-phase Flow in the visinity of the wellbore for uvier- saturated clls. Muskat 121) presented a simple Spproash to stdy the effect of tworphase flow ftbout the well bore for a gas condensate well that could be applied to a saturated or under- saturated gas condensate or ofl well. s (a,t) POR CONDENSATE WELLS Muskat's equation to calculate the rate of change of liquid saturation taking place about the welltore for a producing condensate well ie: co a ae # e@ #.... as Firag Saturation 4e assumed to build up only to the Limiting equilibrium Liquid saturation; its radius then expanding with tine, For a steady state pressure distribution, and saturation S equal to 0 at t-0, we can obtain an equationSFE_1529, M,_J. FETKOVICH 5 in terns of the approximate radius of the eiullibriun tro-phase flow region, In helneoring unite it ts 2 ron DU ag WEL. 408) Top ¥ fie BS.a, vnare T 49 oxrrossed as reserves exbie feet of Seelannate sosunulstion in the reservoir pe Meetor teat vollotroun gus Prodveed peF Fi, 38. can be exloulatd using the retrograde yutd volun data doternined from PT station, The tore dono the stitionl fpamosarton ial Mareen US eaoh equiliorhun ov aobtt Haute steeeton, “ame athos pertinent anise are Hoods Storr dyes fee and oaey. ‘The definition of skin effect (3) in terms of the radius of an altered zone r, (equilib- rium tvo-phase flow region), and tite reduced permeability of the altered zone ka, can be expressed a8 an | + (8) Equation 18 defines a rate and tine depen dent skin term that can give the appearance of non-Darey flo¥, The equation, although approxiaate, gives a simple analytical expret sion with which to estimate the effects of two~ phase flow in the vicinity of the wellbore. The significance of this effect in condensate, wells has been denonstrated by others,14,),16, 17, "za, 18 has been used to successfully analyze the results obtained from isochronal tests on condensate wells. A significant por- tion of the skin was attributed to s(q,t). 2 (ast) FOR OTL WELLS In thg studies of West ot al 2°, Perrine’? and Weller, an analogous behavior around the wellbore has’been shown to exist in an of] well, Under constant rate production for initially saturated solution-gas drive reservoirs, their results show that the gas saturation quickly builds up to the equilibrium gas saturation (critical gas) and renains constant at its equilibriun value, Ite! radius increases with time until the wells drainage volune is above the oritical gas saturation. (See Fig. 4) This zas saturation build-up in the vicinity of the wellbore is connonly referred to as "gas blosk". The corresponding of] permeability reduction in this region 4s Substituting Bq. 16 into 17 we obtain (ic = ka) s(q,t) =a ln 1135 4, 2 vere ea W Fer an therefore constant, with its radius inor with time, sing This damaged zone within which the relative permeability has been reduced has been referred to as a pseudo-skin by Weller. Utilizing Eq, 18 with the appropreiate variable substitution, the rate and time dependent. skin 8 (q,t) for an of] well is (k-&) (a,t) = story spree cers ae Se erage mere r gk readily obtained froma standard PVT study using ‘the Mberated gas data R, as a function of pressure. Sog is the eqiilibriun or critical gas saturation, fraction of pore volune, Other pertinent unita are STK BOPD, ops, DAY, FT, DARCY and RES BBL/STK BBL, ‘he results of West ot al were first used to deteraine whether £q, 19 would reasonably predizt the radius of the "pseudo-skin" for {ines before boundary effects becane significant, Using the basic data given in their paper and Bq, 19 a caloulated r, = 1,6 FT versus their 1.5 FT was obtained a€ 2,21 days, and ra = 4.6 FY vereus their 6.0 FT at 16.8 days. fgg, 18 or 19 are applicable to initially saturated and partially underssturated reser- voire, Once an ofl well's drainage volune exceeds the equilibrium gas saturation £4. 19 {2 no. longer applicable, For condensate wells, Bq. "1@ will apply for a much longer period of tine, at least until revaporization begins to take’ place. Then rg Will begin to recede. Only dn the case of undersaturated reser- voirs, we could assune that the two-phase region ie at’ the equilibrium gas saturation and exists out to where the pressure is equal to the bubble. point pressure, This simpler approach, develope: by ‘1 for wells producing from under saturated reservoirs, leads to the macimun reduction of PI which could be expected from a gas saturation build-up around a well producing With a flowing pressure below the bubble-point pressure, By analogy, the same approach could be used for treating undersaturated gas con- densate wells. For completeness then, Bqs. 12 and 13 shoulé be written to include a rate and time dependent skin, s(a,t). We would then have 7.08 v0 (P-Ryg) a aq [ERA Tey B (wey )y By +5 +s (a,t) +09 wee (20)6 ‘THE ISOCHRONAL TESTING OF OIL WELIS SPE 4529 and 7.08 ich (m (Py) =m (yQ)] 4 @ WB Rt an/——A 545 (at) +o ..(2) Hua), Fy After Raney”, we can define stestt. 1 ee ee ee (22) and s"=ste(at)t+to. 2. . . (23) WELL TES? RESULTS ‘The basic results obtained from isochronal back-pressure tests and flow after flow multi- point tests conducted on ofl wells are summarized in Tables 1 and 2, Reservoir fluid states in which multipoint well tests were obtained are, in chronological order, 1, Gas saturation existed throughout the reservoir above the critical or equiliriun gas saturation. 2, Undersaturated reservoir with flowing pressures obtained both above and below the bubble-point pressure, 3. Saturated reservoirs with the reservoir Pressure at or very near the bubble-point Pressure, Ay Undersaturated reservoir with all flowing pressures above the bubble-yoint pressure, ABOVE BQUILTRRIUM SATURATION Stabilized flow after flow multipoint back-pressure tests were available on 16 wells producing froma solution-gas drive carbonate reservoir, Field A. Reservoir conditions were ideal for testing the hypothesis that do vs. (F2+ Pye?) would plot as a straight line on ‘log-log graph paper with a slope (n) of 1. The reservoir variables in this field closely approxinated those used by Vogel in his study, (See Table 3). Average gas saturation in the reservoir at the tine the tests were conducted was estinated to be between 10 or 12 percent. Fredusing gas-oil ratios when compared to the Initial solution gas-oil ratio of 681 SCF/SBL Indieates that the reservoir was well above above the equilibriun (critical gas) saturation at the tine the tests were conducted. (as-oil, ratios increased only moderately at increasing Grawdowns for most tests, Although the unit slope did predominate, four wells exhibited back-pressure curve slopes much less than 1, 4 slope less than 1 results in an even more rapid decline in rate q with drawdown than would be predicted from Vogel's TPR equation. ‘The test on Well 6, Field A (Fig. 5) consisted of seven individual flows, each to apparent stabilization, The first four flow rates were run in a normal increasing sequense. Following the fourth flow at 229 BOPD, the rate was reduced to 93 BOPD then again followed by an increasing sequence of flows. All points essentially fell on the sane line, indizating that transient effects were not the cause of the deviation from the linear relationship predizted by the productivity index concept. Note that the flow points define a performance curve with a slope of 1 alnost to its absolute ‘open flow potential (AOFP). Table 1 shows that, for all wells tested in this Meld, the maximum flow rate was very near the extrapolated absolut open flow potential, In the other fields in which multipoint tests were conducted, equipment Mnitatdon precluded defining the entire curve, requiring « greater degree of extrapolation to AOFP. Well No, 3, Field A, (Fig. 6) illustrates the most significant result of this first group of tests, With an excellent alignnent of five stabilized flows, the slope of the back-pressure curve is 0,648, The results obtained from this test first’ suggested the possible existance of the sane lower limit of the exponent (n) as exists for gas wells (n = 0,500), and a non-Dare; flow effect. Well No. 14, Plold 4, (Fig. 7) exhibited ‘the maximum increase in gas-oil ratio with Increasing dravdown of all the wells tested. Even with the gas-oil ratio increasing with rate, the slope n of the performance curve was 1.0, UNDERSATURATED RESERVOIR (p> p, and Ry¢ = intercept of pressure. function £(p), ep.73 formation volune factor, reservoir vol./ surface vol, = total compressibility, psi a © = back-pressure curve coefficient D = non-Darey flow constant, (STK BOPD) h = thiokness, rt. J = productivity index, STK/BBL/DAY/ped. J! = productivity index (back-pressure curve coefficient) SIK/BBL/DAY/Uped) 20 k = effestive permeability, Darey ky = pomeability of altered or damaged zone, Darey kyo“ Felative permeability to ofl, fraction n(p) = pseudo-pressure, (Seo #4. 14), Fsi/ep.SPE 452 MJ, FETKOVICH a n exponent of back-pressure curve ACKNOWLEDGMENTS PB wverage pressure, pel I wish to thank Phillips Petroleum Co. FR, = Dubble point pressure, pai for poraission to publish this paper. The ‘ 8 support and assistance of numerous people B external boundary pressure, pela in our International Department is gratefully Fy = Teservoir average pressure (shut-in acknowledged. pressure), psia REFERENCES Py“ Anitial formation pressure, psia Pyg ~bottonhole flowing pressure, pela PI = productivity index (J), SI BBL/DAY/PSI q = surface rate of flow, STK BOPD = radius of altered or danaged zone, ft. 3, “external boundary radius, ft. zm, = wellbore radius, ft. Ry = Gas-oil ratio berated per barrel of residual oil, SCF/SIK BBL 8 = skin effect, dimensionless = skin effect caused by partial penetration of formation, dimensionless a! = total offestive skin effect (see Bq. 22), dimensionless s" = total effective skin effect (see Ea. 23), @inensionless a(q,t)= rate and tine dependent skin effect (see Eqs. 18 and 19) dimensionless S = saturation, fraction of pore volune S.4y 7 hydrocarbon liguid saturation to achieve nobility, fraction of pore volume t = time, days T reservoir tenperature, °! X = reservoir cu. ft, of gas evolved in the reservoir/STK BBL produced/psi, (de/dp) in &q. 15 Y = reservoir cu. ft. of condensate accumulation in the reservoir/MSCF full wellstrean gas produced/psi, (de/dp) in Eq. 15 2 = gas deviation factor, dimensionless u = viscosity, op. Y = porosity, fraction of bulk volume SUBSCRIPTS 4 = 4nittal o = oil ge = eas he 10, n Swift, G. W, and Kiel, 0. G. Rawlins, E, L,, and Schellhardt, M.A.» "Back-Pressure Osta on Natural Gas Wells and Their Application to Produstion s", U.S, Bureau of Mines Konograrh Cullender, M. H.: "The Isochronal Perfor~ nanze Method of Determining the Flow Characteristics of Gas Wells", Trans. AIME (1955) 204, 137. Moore, T. Vs: "Determination of Fotential Production of Wells without Open Flow Test", API Production Bulletin 206, (1930), 2. Bvinger, H. H. and Muskat, Ma: "Caloulation of Theoretical Productivity fastor", Trans; ADE (1942) us, 126, Vogel, J. V.: "Inflow Performance Relation~ ships for Solutdon-Gas Drive Wells", J. Pot. Tech. (Jan., 1968), 83. Fowan, G. and Clegg, M. W.: "An Approximate Method for Non-Darey Radial Gas Flow", Soc, Pet, Eng. J. (June, 1964), 96. Smith, R. V.z "Unsteady-State Gas Flow into Gas Wella", J, Pet. Teoh, (Nov., 1961), na. “The Predigtion of Cas Well Performance Including the Effect of Non-Darcy Flow", J, Pet, Teoh, Gury, 1962) 791. ‘AL-Huseainy, Re and Ramey, He J., Jrey? "Application of Beal Gas Flow Theory to Well Testing and Deliverability Forecasting} J, Pet. Teoh. (Nay, 1966) 637. Av-itussainy, R., Raney, He Jay dre and Craxford, P. Bi “Ihe Flow of eal Gases Through Porous Media", J, Pet. Teshe (May, 1966) 624. Raghavan, R., Soorer, J. 0, T, and Miller, F, G.: "hn Investigation by Numerical Methods of the Effect of Pressure-Dependent Fock and Fluid Properties on Well Flow Tests", Soc, Pet, Eng. J. (June, 1972), 267.2 TE 1SociRONAL TESTING OF OIL WELLS sme 4529 12, Moskat, Mes Pigston) Prinaiples of 01. — | 25, Vatrossy Jey Harms Cy Zep Uaredng, D. We Progustion, HagrarcHiii Book ocr Tns., and Heeadesy Vee? tetitot of 2eak New York (1949) 793, 126. Stress on Gas Production from Low- Ferneability Reservotrs", de Pete Tach, ‘13. Muskat, M.: "Some Theoretical Aspects of (Sept., 1971) 1161. tycling-Part 2, Retrograde Condensation ‘About Well Bores", O11 & Gas Journal, 26, Brons, F. and Marting, V. 5. "The Effect Reprint (Cirea 1950). ——SOS~*S of Restricted Fluid Entry on Well Productivity", J, Pet, Tech. (Feb., 1961) Eilerts, C. K, et al: "Integration of 1y2. Partial Differential Equations for Transient Radial Flow of Gas-Condensate Fluids in 27, Standing, M, B,: "Concerning the Calculation Porous Stractures"s Sees fete End of Tnfley Porforannce ef Walle frotusine (dune 1965) 141. from Solution Gas Urive Reservoirs", J, Pet, Tech. (Sept., 1971) 1lsl. 15, Gondoutny May TEthy, 2. and Hasson, J oe Bets Teche Tan Rebatee fo Fratlet'the Tine Dependence | 28, Lavine, J. S. and Frate, Was "he Galowat er helt liverasilicy in can Condensate Forfortance ot Solution-Gas-Drive faser~ Fields", Soc, Pet. Eng. J. (June, 1967) 113, voirs", Soc, Pet, Eng, J, (Sept., 1961) 6, O1eLLy He Gs and MiLLe, Ry: "Success fully Gveltng 2'tow forcaabiatty, Hager” | arrewure 1ield Gao Contensete Eeservoir"y J. fet Tech, (Jan., 1967) 41. Equation 6 17. Russell, D, 04: "Single-eld Performance Preciations for Gas ondenaste fesorvoirs’,| que —Za08 kh Paper SFE 4072 Presented at the 47th an(2) +s fakeet fall Mostings San intondoy Texas, = (Oct. 8-11, 1972). 18, West, W. J., Garvin, W. W, and Sheldon, % Sr'W,: fsgidtdon of” the Bguations of Shstandy-State, ho: Phase flow ip O12 | Lf sateen a, gm] oy Reservoire", Trans., AIM (1954) 201, 217. | [Pyp u, Be wD) fot 19, Perrine, R. L.: “Analysis of Pressure can be used to describe all three possible a. 22. 23. Buildup Curves", ling and P3 Pragtiee, APE (i956) Lae Weller, W, 7., "Reservoir Perfornans During Two-Phase Flow", J, Pot. Tech, (Feb., 1966) 240. Handy, L, L.: "Effect of local High Gas Saturations on Productivity Indices", Drilling and Prod. Practice, API (1957) i Ramey, He J, Jr.y: "Non-Daroy Flow and Wellbore Storage Effects in Pressure Build-up and Drawdown of Gas Wells", J. Pei sh. (Feb., 1965) 223, Vairogs, J. and Vaughan, W. Ry: "Pressure ‘Transient Tests in Formations Having Stross-—Sensitive Permeability", Paper SPE 4050 Presented at the 47th Annual Fall Meeting, San Antonio, Texas, (Oct. 8- 21, 1972). MeLatehie, L, S., Hemstock, Ry A, and Young, J. W.: "Effective Compressibility of Reservoir Rocks and Ite Effects on Permeability”, Trans, AIME (1958) 213, 386, flow conditions that could exist for a producing well at some time during the life of an initially undersaturated of] reservoir by eliminating any terms that do not apply over appropriate pressure ranges. ‘Le-Phase Flow: py> Py» Py> Ry OF BE By A, STEADY-STATE FLOW, Constant Pressure at Outer Boundary 7.08 wh | (Pe - Fs) ° bs (2) +2] (> %o) 3B, PSEUDO-STEADY STATS FLOW, Closed (NO FLOW) at Outer Boundary Ls! see Gd) a) Boundary Pressure p, is known at ry (Initial Isochronal °Test)SPE 4529 M. J, FETKOVICH 3 v) Average pressure jj 1s known (J; = shut- | 4, stBaDY STATE FLOW (Constant Pressure at in preasure) Outer Boundary) 7.08 ih (Fa ~ Pye) , ee a | en Oe, Fe) 346] 5 % 8 [a (B-2+ 8] [is “| f ¢) TRANSIENT FLOW “ Pat 7.08 h (Py - Rep) 2 ~ Fy) ¥ 0) | Gael. ee HD an (Be 4 ot |(ZB) ‘v0 Pe? V gue); *, ee B, PSEUDO-STEADY STATE FLOW (Closed (No flow) ws Fw at Outer Boundary) LL Iwo~?hase Flow: py.< pyRS A, or Hye py» and a) Boundary Pressure p, is know at 7, 355 (initial {sochronal°test) zg ee BL 08 kh. Kyo (SsP) ay A, STEADY-STATE FLOW [Constant Pressure at i re ae Outer Boundary] pats) 3+ “| Fo Pe ic, (S,p) Fw Pet 7.08 kh ‘ro 8 dp 2(A-5) Ip = rs UBS ( ) Ze) 4g ° Py ~ bl) ‘Re + Gee]. ee a PSEUDO-STEADY STATE FLOW [Closed (No Flow) oO Pae a Outer Boundary] ») Average Pressure Fi, 48 known (Fy = Shut a) Boundary Pressure p, 19 known at 3, in pressure during“ depletion) (Initial Tsoshronal Test) ° 8 kn 1 Pe Kpo(S+P) 40 % = ° Be aP (4-6) fan(38)- Re “| Ah = o(55P) ay . (Fy P) ») Average Pressure jp is known (Fp = f fF ap, Ped an) Shut-in pressure) ® ‘oF OO Fae B; Be = 08 kh R Kyo (SaP) ) 4 7 ba) -2+ “| he C, TRANSIENT FLOW oe (4-7) = ———2.08 kh we 08 ih . # (we); 023 t 7 o [»/22, +] al [2 8 2]. um a Ree “f KolSP) ap ek ke eee (AB) 121 of the preceeding flow equations sould eto be more simply exprossed in terns of a pseuto- Pass Pos Pe? Py OF Fie Pa pressure? a (p) where Pe mere Fey oF) ap = ub, ‘oo ReME TSOCHRONAL Tas" STING OF OTL WELLS SPE 452 For the lintts PVT properties = 1) we have case of at least using known ugBy), — (assuming k,, (S,p) aa, (PQ)-By (Py) “a5 Pet + OO Py Pye a Py Pe-Pur WE ee ola NFO) avg (35) Note that (u,B,) normally evaluated at. the prorege orossure’ (B19 )/2 would not reault in a properly we: rage. But for the decline in ky 0(5,P)y 4 plot of a, v3 (pg g)/ CB dayg “bed plot a straighicedth aPelthe of 7.08 iestan =) + 9°] and fiSreept 0. Let us now consider the case where k_. (S,p) decreases with increased drandown, k. ula approach 0, resulting in k,/(y.B,) Tproaching 0. Aoouming,Ko/(u,Be) could be approximated by straight 1188 rufcGions as depicted in Fig. 2, we could write for the two-phase region. Po Po Bet We + (4-16) which when integrated between linits yields ES a Jf £ 0) ap= 3? - ry) + by Cry) Pye (A-27) To approximate Vogel's IPR equation we set b, = 0, then’ Po a fot) p= Be - ye). (re) Pat Replacing p, with p, for the two-phase flow equation (Fe Sp), we have 2.08 az) +0 ; % 2, we] ss a G2. [2 = The slope ayy for by =O, de ataply (iepg/tgBo)/Fqe We thon can write 2 , - |), Sgbe |... em Pol Fg Py defining yy = 108 ki 3 fe naaf22) + 29 x, = sone « (42) (3), (=) ww then Gg = IS Be = Bye) we ee ofle22) Stndlarly treating the single-pigee flow region as depicted in Fig. 2. (pie r,) = 8 i * [= i") eee ae a) Tn terms of FI at a vanishing &F, ops = TRE ey a gd + (4-24) call) «+9 where a, or byy if ay evaluated at Py » is simply (k,/,8,)SPE 4529, M, J. FETKOVICH ty For the combined single-phase and two-phase flow case we can write TOR ap (Peder 80 (my mer) + (OerRy $ -(A-25)] where (u.B,) 's evaluated at the average Fo) pgm, 28 tveluated at th ze 2 pressure (p,4p,)/2+ In terms of PI definition =, Boyan, (22) He Bar) * Jolerry) = (4-26) 9 93 (mR ye) + Ig (Pym) © + + (27) ABLE 1 - PIBLD A - CARBONATE RESERVOIR AT 5,2 ‘APTERFLOW RACKPRESSURE TEST RESULTS, GAS’ S GAS SATURATION. ‘Shut—In 00 FP AND 108°F, SUWARY OF STABILIZED FLOW \TURATION ABOVE’ CRITICAL OR EQUILIBRIUM AVERAGE STABILIZATION TIME 48 HOURS, FLOWS IN INCREASING SPQUENCE, Bagh-Pressure, Curve Nunber a Bp OE Slope A Well No. Of Flows ‘STK BOPD PSIA SCF/STK BBL a BOPD 1 5 1339 370 619 2745 1,000 ‘420 2 5 1347 468 9 3202 0.875, 670 3 5 1200 292 530 2572 0.648 340 4 5 1307 3k5 563 2181 1,000, ‘425 5 5 ial 238 She 3571 1,000 310 6 7 1345, Bal 638 3945 1.000 AAS 7 5 1215 222 520 Ab8S 0.771 275 8 4 él 16 375, 2019 1.000 U3 9 5 159 202 436 3219 1,000 243 10 7 1430 261 Ag 1056 1,000 295 n 5 128 126 395 4008 1.000 165 12 A U7 321 578 1003 1,000 375 13 A 878 na 379 5979 0.707 3 uy A 10 208 632 4607 1,000 260 1s 5 1366 108 370 3805 1,000 123 16 5 lay 106 ‘357 3397 1.000 110aa 2 - Malo © SSK x GmARE GRE). smo so SOS, CSRS "atrnelans, oor ho (ROEM NEARS (0 SrA SE RE EA cue AREER CE RP mF ah sorysm APT 2 ro me “ BL muon ma = me ew eae {2 oe me 7 Dr 3}, 82 2B i BME 1 i i Eee Be 2 2 z 3 3 . 5 106 20h OE Ok 9100 . n » wm Mm ce ee 22 wf B 2 Bote g 2: 2 8 Ba FE 2: 3: 8 oe: ¢ 22 2s Big é Sp mm 5D. 1568 720 . 32 cd Be a2 a er ae Ze 2 oS #3 Be RF te oF suo ay 639) sa en ame em mt = my =z: 3 mi ams Fe fog PEE pe me gue ae as ag own 8 PUY : RB BR ME me Se EE rat re ky ak onsen mm aes » = ha 10 » Re nes wa s pe Be > a Bs 6 2 sBy &rope, oe on se EERE PRE ne aman Tones oeees Deu ee OVA 2 ae ee 2 ws mk - 2 woe asm 5 wus ‘ vos mma , wae hake een Pana oa kn bn 0 Bese er am vee w Bek Se 1130 x Booms ams ase we momen a8 ophem Ttof /2002 3.9 3880s Dore dss sms 37 ber as sso eee aa m0 ee. 35.7 . om Se soko emma” PON ROR noe Se a =m am oe sero Data = 2469, puidnp Bore sta. By = 2098 a see mt 8209107 ts oP yom ect, ra ey onte Som et Danita. we ome) 3° tas 2) s sx aire sae (6 0 +n eee zo a we ay use aa 26 2 = oa ma oa An Sor St arun 4, plot ried 0 san strayed Us ‘AS 7 WR Ps TSO ESN OF WE Boy BLD Pestse Eeprnter ree Bag oe ieee ce Reh appre senses ms sa - = 2.7 Poteationy, BEW/2I , moms me. use 2am be a sos ae pe a poss ams ure 22. wok 77 96 ve ome tas 1 ~-0.F Eectapatons 6/22. 1 jane jms ge 2 yeas 6 aa on 3 ses sam re 193 © bonkers me 2 ee) ps ussuse — ne Feet EERE te aad ES er EEE OREEE aes aeons "RET Snes : See ews 3} wm emma (ee wen am ws we me me sm toe oem + tase ww tom oe wm ‘ae 9» 8 OF SEEM HAGE To FOEBOGE aos oF FL eas eessuRE muETON® by hy = A78 pats ODF Meg MOTE HAS Pe ry 0.33 ts = 1058 (0 woes) yg 7009 2 Fat = 02 (aenmad tobe estar Hadad ptt, Hg 040K 88 29525 STE OL; = 25 and 2.5 Oy 5 a fe yee geet kala asta (Trmumante) (Mounts) PL hsumacte) a Sade Hat) cra, 1 = 25M Sg = 0995 an 0.09727 SOFC Mamrane ota) aoe 6a 7 xo SCN ae arts 1 lee we 93 shat wa mn 1 Tan oy bas noe 1 Tom saz 303 fe aot A= 25 MO} gg OK ont 603070 sORO/(Mautn pia") we 1 an DO Boe an 6s 1 an Take Bae ae on ‘ wp RE ogee mo “ we ew Meat 1 ela STL 5 ogy fg ot eae tea) Da408 wis-% ooot=u aun s9=e30¥ vse-nussnue sononseas (46) ania ounseman Pe 00 one cuca vas =°% ome Oost oooh ons mows omnbr 36vHa STON HOH 0+aL o-FLow AFTER Fuow neat: qe 3107 Apne oFP=5900 80" J igaegacan FP. 2008090 meonse 000 000 00 awe? serSTA BORD to smsoro, 012/207 Fy = 8085 pe si esr _— 4, ei eee Bye 3m.0 pa Mires ras0 80m | | “000 ‘tor 5TH 8000 hq 36953 900 n8ye= 600800 mous Arg cwouwasy cosocinona, | Flow aren now |‘00 —— ¢ (Flow aetes Flow og g a2 3 An “Page, I Sip t ‘ool ged ‘wooo sore) 2 Lope 000 ‘00 iow so STK 8070) fon 3Th 20%nO gece ae ee “OE 2 wo 2 500 " 4 or omnes 4 4 [CALCULATED PARTIAL PENETRATION SKIN, Seas ) f oy stoi 06 —— 082800 esta 2oro pat?) THOUSAROS Ic, 4| LoDRAMOONN AT TIAL CONDITIONS A 2-(aguandEPLETION c0°STH BPO a ito tS rc ac) sans, sorpeta300 2070 // mone vf © tsocnnowa, f Ftow arTeR OW PnP pos io ae wae fi Tar