Scribd Logo
Upload

Welcome to Scribd!

  • Chap8 Hubbard PDF

    Uploaded by

    Santiago Torres Pacheco
    19 views37 pages

    Original Title

    chap8_hubbard (1).pdf

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document

    Copyright:

    © All Rights Reserved
    Download as PDF or read online from Scribd
    Flag for inappropriate content
    19 views37 pages

    Chap8 Hubbard PDF

    Uploaded by

    Santiago Torres Pacheco

    Copyright:

    © All Rights Reserved
    Download as PDF or read online from Scribd
    Flag for inappropriate content
    of 37
    ss 8 Systems of Nonlinear Differential Equations "The general wooo dieetin oaation on ie (0) x =the) = a a fi), ‘ntfs be hoop of a vector lon an open mbsf He (oores the evolution of lnumerabe actual poten, and even tbe Owo- ‘Smpensonl xs fen v=o) o as 8 et many tps “ahapler? wo sled the cam ware saa his chapter, we concentration anne equations, Of ons over wan = we cannot ‘pet te ot of detalod everption that we un te ier cvs, After [IE telnet cre depends oly four parameter, whereas Ue ona ‘te depeds on init any ince f aad gar both aitraryfanesony, ‘ements fn nite mension voter space. [Actual fad gare nat (pate rity they mt sty «Lips condton fr oquaton (1) to ‘ve una eto hugh eet pot and practic, wil usual be ‘mguted to be ws eontincnaly dere ‘i, we wil gets surpeaing amount of inormation shout native ‘stor lier or sal the nea! case aoa from eration in ‘So densi x ar , Cana 8) "Weil in Serna 8:8 that aoa te svete of the vector Sl (the pints whee f(x) = te boavie of the dient equation [ual controod by the nen pproipsoa to the wstar Elda Dot The Hoes problem ie peclely want we tud In Chapter 7 ‘Then ia Secs 8-0 wel sand bck fom the moet ands wat sre cen sy about th bal tei of nonin sats In dimension “The two-diensonal yen (2) in Ri mest mena to anal ‘the funeons f apd g do aot depeed expltly on te hs maling ‘Sree (2) taneous. We traw fom Section 2 at i makes sete {hexane the ajar of the autos the 2y pare plan, because {can astnomoun eee thre rjotere wl wally aot oss (roe thre the Fence and Uniguenes Theorem 623 fl). 12 Sytem of None Dion Equations (Cares inthe pane whic cannot inane ares stone onetrai that “cho cannot appar In dimension tre, howe, aeons have ‘ery apport toot laa tangle Te cused eral in Secon 87 apd 8 but seal proat aze iit anda ered ‘ie Chapter 8 here me can fal fice delous to erlain the cat pos, Chapter §* coasts of many dacaioneexoading the tops {tlc eet Chaper 8 ‘One mre tpi that bongs br jp the intadaction to nliner ifr cata oqation ine that of mmc snd vole ering ios, wich appears as Seton 36 (bat dura bare companion sth tn Chapter Caper 8 an be etedod by von lane rotes: + Aftor edi Scions 7 and, you may g ety to Chapa 8 + After rating Sotons 87 and 88, you may read Chapter 8° and ‘thon go onto Chapter 0 + You marta scone of Chapters and lle: £1, 8.1, 142, 82, and soon though 85,875, and aly 6&6 In tis ast you wil nd ealighteniog to read and 88 bee 3 and ‘A Bower ge in the Prefs to aly tht aggstios. ns chpte, we stl consider meaty nonlinear atone eens ‘nthe zpplanm Oncsinaly Ho stent and pal ae herder | Rand tar we wil do things ia moe gears 8.1 Zeroes of Vector Fields and Their Linearization Locat. AND GtonaL Bruavion oP A VECTOR FIELD IN THE PLANE ‘Example 1.1. Coosidr the dient equation ati ° 1.4 The drawing i the phase plane Ie va forth valu @ = 1.28 and shown ln Figue SL. & ‘Wo in Example 8.1.1 tha he trjotores just fom syst fear ln th plan, more ols purl on «al sae exept athe i pote (God thre are calyx) where beth” and ave aero At the pate he vcr fl vanishes, they ar ele the src of the wet fd .. 4 (81, eros of Vator ls nd hr Linsariztion a (omesines singer points or singularity). Beane the seats ae the ts whee the system rat agit, they ae also sometimes ala ‘air epectally for physical rates. PIGURE 8.3 ha pe place fr sation (2). Oba the epi ware ‘ctrl ie, i th ated can Delintion 1.2 Lat = (x) bea deen equation dein in some recon Uf B°. Thee opal xy where (vq) = 0 called 9 seo oF [ilo pit of the deren ogo ‘I particu, when = 2,» peat (zoo) «20 ofthe diferent ese) ae) 4 fen) = eas) =. ‘earth sero the lions fom patos that hold be fair: thay Jed eth dang we oa in he ea a. ‘Mote prsinsy pint look ke node suren, lok Hie piel sce lo ie apa sink, and B,D, sod F look esol, We ‘Shall now ive rongh of why Us by showing how to contact ‘ Boauaed equation ot oh axa LinBaRWZarion: LOCAL BEHAVIOR NEAR SINGULARITIES 16 § sd ae tn coin diecetne neat 210 (esos is thf! to expand thon Tuo ply aoand this pin (-w) + Ple~sy9—w) fen ay) 424] one 6 8 Systoms of Nonlinear Dirt! Batons stone Bl temas Zt] om 4am ae. ee Srctanreneany -semenmnemeaens Bai ciat aeons noes eee tence as eee eesti fore rim ‘and tao nly the Best ede tans of tho Tylor plyooials The cig! ‘oan ileal union GT - (es) ® is approximated by - (-les Ser|el - @ ‘whic eal the nearisation ofthe ey (2) wee (cs) ‘Bxamplo 8.1.8 For the dient equation ofthe damped panda, 2 y= "sne—y, . ‘he plats (0,0) and (0) ae srs af he vcr Sel “The isereaton a (0,0) i GI-[ Alf): ® swe paramotrs (1,1 in the race dterminun plan. Ths he ae {lon a (00) a apa sink, a howe a Figure 81.2 "The Unaration a (4,0) ie (I Alt: ® vith parameters (~1,-1) inthe tsoedetrminant plane. Tha, the Ia avzain at (0) ale a alo shown in Pigue B12. 1, eres Vstr Pls andthe Linearization 15 FIGURE 82-2. Th pase le ution (8) The wot (0,0) 8 a sik the ee (29,0) asain & ‘Bexmple 8:4. We tar oar opening Beagle 81 areee ® ‘f(3) fo) fia), ‘ea tne dfrantishle wetor fi on an open sab U of, Tea ano off The lnsaration fhe dierent eantion th nar iret eution eae, “ here 18 4 Systems of Noonan Dior! Bquatons Scaasog-20y soot ieaeinad eames eaten % 4, Det Vator Ps nd Loan Ps “ Bib *] A We, Ble By Tipe’ There, we ean wato ffs) = AG =x) +(x), re i) ara with quate arms a) “thou seem x(0)—mu Pendle 0 ern a rn tp) he sean of ner ton of etl eens = ‘hose of ts nearzton We cll this ping cater than tor, because the em tok ened ll oman aden, becuse ea ae ll st things depending oa whether th neato’ uation has neo = Sure or whatever, What we wil do in Seton 81 and 82 Isto plck out Boat i seam goae e FIGURE £18, Blwwp tom Pg 1, wth toch nto emg he nara quan tho properties of pastels interes a how that they go over tote nots sting, "Furthermore us abate on to eaveat“n geo Principle 815 te fae when the mati A Bas any purl imeginary ‘toenutce om partic, f ny elena ae 1 he planets coreponds to the to flowing es: (if 2A=0 and det A> 0 (implying “cater for the nesaton) vwesallshow by oamplothat almost naything can happen. For diferent vation with the same Enearztioe, we ge very deca ests nthe ‘nie ce, Example 82.7. Coss the diel eqetion GI-F2}ef] ® ws sya ten Dia Han oat. ind eu si tT -[]-t oI) G- o ee {lo} ar ree, Heme, th sation ofthe concer sym (0) spa foul > Oand gal init e <0 sea ‘Wo cn male fr mare completed examples for lastance, Brame 18453 whch ba nitty many pedo soltions. (i) 1740: A-~0, the ination degenerate andthe incr vector eld vats senlly on Ine (evn al of) Angas a rie Sy smal prtrting tom can ato Us tu, so ean he appearance tthe petal ctor Bld ea diferent rom the pearance of helo. Bxample 1.8. Conder th gytam of equations on ¥ ‘orci 6.144 ats yu to id the ncarantion, to show tht an eae ‘the neared oqution Se, ad to show tat thn eqaalon dows not ‘tar tela netation ay ‘Remark. In Chapter 0, we sal xamioe gota cass apd chow that ‘Beample 817 lens to "Hop bfreatin” and Example 81.8 lads to “Seddlenode fein” In the plan, fal signals hve a nonnro val part Price 8.8 mea what ise, Thre ied way of aking Hs statemet= By ‘inking a moot eoaines) change of varie north equim pict Yestcat maketh equstion no nara; you can een re at the deimtine of the change of vacates bo the Ideatey at thon. A ‘pic way of ayn hint the space of trajectories were drown "noo rubbr paper, ha ou could stetch and stert the rubber test, eth the trajectories of th egal equation wil pracy on tsa the linearization: you can even Mp your thumb dova onthe oly Dy hb Hing the pot aad the ange vcr, a ree the ‘bier shoet fom moringo tain wou that pl "The poof of th rel in tat frm i ute datat, so we wil ako a 0, Then for any C with 0-< © < A hee el acs of Rin ich dese < “Ci for eery = Proof Toren 1.10 asserts: fA has pais of canjgat nonzl gen- ‘bi thee 8 bs win OF sah tat fr any 6 {at ba prado pper-tangir ih tems of bala wiv how the peeudedingoal Esercne 82845 as you to prove th where As the age real part of an lene. Chas e< (AG), {the emma lows. CL Ima. FIGURE 621, aati patos of uso Now we can del wit Ue nonlinear eas, refering to Fig 82.1. emma 8.24. Det A be a rl mati satisfpng Ae: < -Cib?, and 4a (x) satis as Cabs for |< Let p = ma 03/203), ‘The ny soa of x= A+ ae) wth OES sates BOM sree prt. Proof This a “fone” conta tet n Fg 8:22: (i @ selon tow = Vg th At) nt) 42010) -200 uy “2CDxCOP +2Cs1x0)1° whenre (|< R. Our don ofp then gives, whe x)

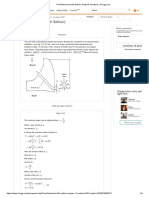
    0 on thie dro C. Let V be the region iside C where [Pre if this 2 sem oighorbood of x, saber than U, and we wl ‘how fat eey slo whic ener Vb atc 0 ‘Seopewe tau) V. Sc the fncsion Po) eceaiog can reve increase to BM fr ¢> ty Hence, to auton wl stayin forall oe Remark. What sak thi pro unplomact is that we eaaot speck of Enr(u() without some pecstion (ight acum on Emit ‘pels me nee naples and no be «Lining alae. We ‘ina tht fran sequence f+, here subeeqnenon pod at co) £2, Souous Are Souci und Sink Are Saks ur ‘ests. This is sinply the statment “any saquence In compoct st hae ‘comungant atasquncy” which you should tale on th if you donot Sow isin However, yo soul alo be «Ite wary tee whee Ue noneonstructvty ie hidden. ‘The “ple” att shoe gies int how tod the robeequen ‘Proof centnan, Tak any wellapacd soqune of ines tending. for Instancs, to neagu, Sao the oqanos Puy) int te oqnce dienes Fein 19) Flats) {nde oO. By the Mean Vale There, there ext me mabey [eons] sch tha a Flan) = Peas -39 Fala) on tent ning ence ol we my sp tat i) ce 4 Gran) Oand o() of the same sgn for x 0.Tis uation i caled [inar's equation and shoald male you thin of te damped harmonic cwclitr the emdten fs) > 0 ajo thatthe fein spol, sad {he condion zg(=)> Oty thatthe fea rally stare. OF coe, te (dary damped harpist equation i spell ne of Liars ation, btn prerelthe equations nonlinear, witht ton snd te ‘toring fee depending onthe pston Te not cl surprise sgn, nt he oii should be ink and 18 6 Systm of Nosiear Dilla Batons Repos to son nda equsin (16) by Ue egualnt system, (FT -Lreats eal Se (a) = f fon and consider o* remot set Note st tnt F dos are an shoe minim at (0,0), since hs ‘Sate tum a 0 nt why wo armed (3) > O02 rand, a VP(z, a) f(2,9) =v Fl2) <0 vi 8) (00 Tee ong empton ht le) +2038 #0, tut ong nent (0.0 eat ee pa Atel, is (htc owe nthe te hen 8 tt a, (kobe sein crepe ot compoc eno She war fl agen een showed tl as hat et Sear rgon we sted eam fF ele mampl vey po (0) the een (aa) < CH C5 Feu te lypotiean on © xy what add io that Sire baat Taner 824397 provir a exalt show sat ca > wang steps mere Sinks AND SOURCES IN THE PLANE ie now kaow ta the inition of wear Bald 20x of Fis Wink ore wen thn the ifort eqatlon x’ » fe) alo ae sink or ‘unc ay, One gh ie mor pre information, at fr eae [ion the pine nes he iner opatons ae complely sie, Foe {Estaot,f he neaaton spirale thn do he solaoa ofthe ones ‘Soren equals io? This doc ton at we wl om sow: ‘2. Sours Are Sources and Sinks Are Shs 10 ‘The case of epral snks. A piel spin enk le stow in Fgue 825, IGURE 82.5, The ones ok Bom Pigue 813. Delintion 8:29. Ife vc ed in RP and x a eo off at which ‘he inarztion of = fa) ba spl sak, we wi sy a Se apr kof the deena equation = (8). "The detnson juste bythe flowing rel, ‘Theorem 82:10. 7x ia spel sak for x? ring eicnly clone og pir eon v Proof, We my change coordinates to pat ya hearin and fw se ‘he land imagiry parson lganvector aba thet es i ‘Seoon 75 tht the dierent eaten wil bof he orm (2), ten the sation x= [f J] +a. 09) Wo would ito know tht the solutions opel Lat 6) be the polar angle of slate (20, 90)) Sac 0 = areany/s), we haw ga Bizey _ wlbeoy + Qe) ~vlax~ ty + Ploy) eae ae eo) 296.0) —wPCowv) oF share P and @ st the condi anton fa ‘We soy in Theorem 822 that if (0) (0) ufileny smal, bas 200,09) wl be (exponentily) smal we = oo, Pstermore since In expression 2) fe the tra other than bare lat eae inthe ‘umerator an quadrtc inthe dentnaor, they gre meting sh teary smal fr (2,9) near (0,0). We so that for aye (20), 30) 160 1 Symtoms of Noon Dien! Kgustlons is chosen sicily eal then Ot) ae constant sgn fr > 0 nd [eG] > Pl for > Of tnmedotaly flows tht the slton ums Intell mary Une aroand 0.» In Baca 82-6340 and #0, wo wil show that Theorem 8210 in| erm ust est penile fhe aeration difleentil eqn at ‘Sito ofthe wetor fal sak wit qual egemlaes, then oe aatons fooot el me "The case of node sinks, A typi oe sn shown in Figure 8.2.6. FIGURE R26, A solo mde nk (To te oppose of th ode source Ala Pigze 8.1) ‘Theorem 82:11. A differential gation in BP has noe sink ati (pir etn at ot sn ik hs (0 All nations ubich ar silent clone to the sink oppranch the Sa tengo toon egendiction oo, (Precisely no trajectories approach tangentially tothe egenction Crrepnding fhe gemaoe having smaller abr ae from nwt eal hers appanch tangentially tothe ipsecton 1h eigen angler aban tl. ‘Proof, We bre lady sun n Tore 6.2.2 iat he singular pat 0 ‘SALE de awaiaion e= ak o we oly 06d to sow tbe tements ‘Shout directions of tenet, nthe ee of de sink, the enzo {av ewo leary independent eisai. Tho prot of There 82.10 ‘ch ease f we begin our anal ing odin that pce the node equa (29) a the Gmoietenzandqo ny, + ng the egemetore a ass which plas hem along the 152 Sours Are Sour and Sake Are Sink 1st 1 tint eso the dirt equation i, for P and @ sting with fa-mt Plea) yaya) tS) here“ and ae the distinct meatve egenaes, and we wl sue fat ~ji =v < 0,00 to pte lnk Ie Figure 8:25 tht, fo every tenet nol onthe ss, the seordaate prone fe than the ‘penordiat; ts sock a rajstony end up tng oth ae. IQURE 82.7. Pasa port fo! = p= ry wth 19 tte rp Spare reams SSmeuincs Serer: peep oprptrarr Seiten mah merece Soci e eee iets Shree oie ces atten fer ace tps Pace it "Funland anual apply to dlftenta enti is one variable, oto ystems; hore, he alectores ofsltion toe eee le ng, ‘Paphos to w 2 = we) cy thinking ofy a a function of, and of 1 P) _goy S Faaen oe) a (Wiking of a a fnction of 1 8 Syston of Nosicar Diora Buations ‘You do nod to wory about the eure along which the denominators sans afr untos (2) an (28) tae ort equation sere {nL in purer, sone of the tbo out fuels or anifinel ate However he curve ofthe equation x = (sya) where equation (2) ‘adn to be dedi twice ilrenti carve tangent othe yas, nd ‘lat he env the easton vy = Qe) where equation (3) falls {be died ra twice diferetibla gave tnget to the ais. As we ll ‘ecu cee of anne wll vay ocd the carves slong whieh {Be dee eqontins lobe dein. "To grove Tiere 42.11, we wl dene thro regan inthe pane, calla U,V, and W bounded Wy curves a shown Ia Figure 82.80 tht (a) Thelen equation (2) i deed i U and Us nner (Go) tnt ll sltions tha eater ay info y incense oO; SE pea, they appro (00) tangs tothe pi (6) The ieee qunion (2) dil in V, and V i an anti. tor (2) wo te ulgomene condos, there exis 2 une njstar waying in Va crass to 0. (6) W i aeo an antgenel (2) 20 the una taetoy speci in (approche (0,0) tanguniaiy othe mas, “Tu mt dacato prt fe root the uae in (), bcos the solution inh etna fc converging, but ot qe fat ena to tay beta the ons: shoul be eon tht sir tatemcot wl od if nd y ac pase ‘nec therglons above bose ons tothink fz andy inreing Proof of (a). The rion U sea fama freing sltons to aprech 0 tanger tothe yas {82 Sourar Are Soo nd Sink Ave Sin 153 howe c wih << and < pf and it == aly) ~ Sins >, tls carve dow inden approach (0,0) tangentialy to the ssi Hower ice < 2, approaches the yan ote slow than {hy twice difeetibl cre tat tangan to the yrs In partic, Salm (2) eden the agian V- OF ex again (2) dein in, sinc eit nly ons cure tanga otha nae ‘Because y atte inthe ogi onder, we bares) = cl? nd [p/n = 1. Tis mss that by factoring yout of the denominator (Fadeence: Pact, Appendix Aon Aspate Development) can write ls Pi.) the ding tn in ys ~(u/ fo! Note that thi od the eg ‘meat e<2,sace AMES! ig contain ner tem inp coated by teams inp oP. ‘ioe 2 n/, we have WG) =—la > oho) foxy <0 and [pouty smal Tas, pat (a) is pove Asai comptstion with w(x) = a) shows thas Visa funnel and, 2 the sume time tht Vian ansifanel, which the st par ofthe ext 9,0). ‘Proof of (6) There i & unique trajectory in the anifune ‘Wi iat ned to find function K(e) euch that in V we have Rew) Ree es ea oe oa fr hate wih dations an vee ‘We compute hr (22), using the fc a (2/9), ) 2 Key =) (ext) EAB) 4 4 ype of Nosincar Dien! Boations Sic yl < en V, vr he leading tem, a we can ake ey tess ss ee ee ee ee Se petee ae ek ay ee kad Rae Sica ee ee — a ena nh ah Re NSS RE tet cn (ote serzneiest aos ow dos conapare ol? Sines, or Ue aganing of, ee ply the Ife > ofa sd eb Cosa acetly sal, we hive Vervinee "dar the owe be gr he oh ofthe nto nae 0, snd we see tht Un uncon 2) ager than the dstne i" eer th tp andthe ota of he ania, poly one alain ean ne hoag the gin, Ths proves uniqueness. Proof of (¢) The easeptional ston tangent lo the 2, eto) = fl for any wth 1 < 6 < 2 The, ence = ic meativn vieh~ tt, and + va ate) este) = Ta - Gor) (FEE) = = "The ding ean (oa! and ace v/a <1-< 8, we be We) < eo. Asimilar armen out oy = — shows that W in stfu. The ‘miguel a the efifoel V mast a ea WY, which oe to Ttangont othe “rhe palo There 8211 ie now comple, 0 ‘he allowing example wil explain wy soalatger exponents were na esry inthe prof the peeing hore, ‘Th ssocltd lina yea slutins whose rjc pars bol = Oy we wile that the roninea gaan iret al bt aanoyng wey “Tus parel manana can eaily be sled: he exon eane- ton alone il WO = Ce" sd the tft equation become sce ye ot me sox0*([[ergerea) -e*(Chive) ‘To Sind te tnectres in hey ps pane, wo need to eine & from the equtions for = andy) rom the ation ox (we et. eelv/Cs, “whieh if insted inthe equation fo (ee of lal + Car, exgeiny en eee icine eieanenaie senses er rear pear 8.3 Saddles etntion 8.8.1. An autonomous diferent eqoaion x’ = fx) in Insel ta 2ra yo Fie nent here bas sai ‘Theorem 8:32. {fan autonomous diferent equation»! = fx) has © sade, ten ther are prc 156 {8 ystems of Nonlinear Dirt Batons to tetris ht ln 09 8 90, tat ogee with x9 form tomoat crv tangent x2 he ne of eigentector ath meine figonaae (he tle diction), = nd precihy teeta tal end toma ot + 00, a teow a frm (moth ore fangent a x othe Hine of igor ith pote ‘Sgenole (te wutibe deta), ‘As wo have seen in Figures 8.4 ad 6.15, the trajectories of Thre 6.7, ale spartsie pial seperato te regins of goa havo, fd acy sac th sot important chests vo undead abot ator fri he plan. A pple Shown wth x parties Figure [FIGURE 8. A mdi wth geovectors and parison, Proof ot Thoorem 83.2 The proofs sla to that or There 62.1. Here als we (0 we cordate tot ace the sale est (ny) a the Gawetiat €= and = (ue te eigzavectors as bls, which lacs them along the xe. te can ea tin fl-[e VE} eea] pee 0 vith js and the negative and posite egeovaues, respectively, and a @ arin with aude ters 3 Sadie 1 ‘ho fart tat tho separates of wsdl did th vator Bel to gin of gout bebarne should remind jou of antfurnel so deed ‘Sinai ets in the proof Az befor real that fomel a 0- ‘unaes aply to dle equtios ie one rca nl to sytem however, te ajar of maton to eptam (4) flow tho graph of talons othe et are fen eqaticn 4 taen ae” =a + PCa) Gl) ation (25) i a satisfactory thn eqston (20 aot dir otal eqntion wherever r= P(z),s0 tht the denominater vanishes, ‘ein purticlar nono of tha thorns about fans and ania are {Fon when this happens. However, the curve = Play) san (imp ly dened) tnzedieretiabe cure anus to the yas (ere 82 1:11, sp oar coe of atone wil eompetaly ool carves tanger to the ra tthe oi ‘Conde in the thal tho (zy)slane the shaded region U, bound show and blow by curves of eg padye? forwome nm <2<0and7> 0, td th igh region V or which 8 Per, y = yw lowe fon Sat y = ‘mv oper fone, ian atc (GV seen anifemnel Tafa as Haas 83-8361. {) nique sation inthe onfuonl: Ea ade to we He Antal ‘Tenor 1.45 that promis aunque clin nV, wo nod fst that V le aroun tifa, bh ie a7 creas 0, and scan that B9/0y'> OVE you dibctiat the quoi (25) for V9), You get o 20/00) (4 P 4...) ee er/on, Ce -E) Oaee) Sarge en ‘10, he ony tem of (27) tht ppc nity (=), sod ie eating term pst nV (09/0 stars with Ha ee, ‘© Gayoays) nt mut» conta Petar nh sane rm, 5 Pye acts wth tet ar orm tht approncne sr 0 (Gah eV wt Gp) ely ee othe ce, 9/09 > 0 "Pte, ne caowig ann we pet th rg, tae sige maton fo the ht! euton (9), Te ia {te equ pu rh omar ee tow neat ng {Se om Sn deal ents href, o tan lon Steptoe som (i) Tange of epee meni tng a he ai te ccemetor it th ete ceva The unqn lon nV lso {tee ction i ty the une argent gen npr (2 ‘Tguan in beens oo pra tng to te ino che ne "Tha, tela eproved, 0 Proof of Theorem 8..2, continued. Al he sates about sales {alow om Lemma 8. app for ee, with the nanasay change 4 Limit Cycler 180 viable forthe four ston in which the aude can be spond ‘Werneed the fw otf to conta the dietion af he apart ‘temo the second ntfnnal V, which oar, to capture al elton: ‘sporonting the alia pont rom he dng! quart, 9 ato ‘rll the Baal argument any “oo man’s In”berwen the ou oad ‘eon of U ow in Fire 8.3, where we wold ot know how the ‘ottione babar I J FIGURE. our vn of U wth or poncho 2 We bee sow prod the theorem. 84 Limit Cycles ‘The simple thing solution to a aifetal equation can do is to be started tan equa. In the preeting ie tons we hae ee Sloed alvin some dota. Th nox simplest for hn etm to Seder pero maton, cfr the phar plane ajctry to bes aoe ‘his behav eminetoscur fr eutonomeas eens In R, sce elo ‘net be enbedded in ine Tn te plan, cys exist and ao relatively como; fr iste, tho scltions of te bam caclatr equation G-[] ™ or noua equation, cys uoualy behave que difrenty rn those msc to nee eganions: they ae arly slated sd contol {he behavior af nary sltions in the sumo sxge tht alia cota {he behlrof sesh elation Ths pepe the ma wey fn ich ‘olga eqatios dif fom Leer equations a lest nthe plane Teles atm 1a the pase plano ths diferent equation prodvoss Figure 84. FIGURE 6.41 ajc gun (2) wit Certainty i apne that al slsions ober dha Ue eaten lation "This bys fc, ite ety to prove This duets equa ha been areal cootcl up to be oar to translate (Bec 8a) ito paar ‘sonlntes2 llows Pi, Te Betas +2 aw Ze Now titling 2! andy om (20) ves (Exar 8.418) cant, 0 oy ts fait cay to ave the St equation of (0), bat ven ene 10 sly it fem ds of lope the plan (serie 8.410): Fora > 0, ‘Sielatons rr > Dare neat ate constant sation = for a 0, ‘he snlutionr=1 i repalag, bd FO r0) <1, the salson tends wo 0, ‘nhoreas 1 0 and ‘a ete (reeling) Ini cple wna a . Sabi mea thatthe ‘ele tract ery ston st fo; tity mana atthe ele ‘Shrets nabyshtions ws f+ ~oo 4 Limi Cyl im In the pls, thn ar he aly Kind of ik pls tat appar “gsc cally (Wea cter“xcptonsl ones” wih we wil examine in estin 1) ta higher cnesony ther ar nny eer nei pois, we wl eter btn Chapter 18 in Part \Conaering tht the exsenco of lint eyes i apr coman orm oohavo fra dieretia eqantion fn he pans amading ow ely ‘hy eam up nes dfeectia guns are entered st random. Limi ‘le do ome up rather often, however, dirt equtions desing ‘eal pesoceat Moreover ewe wilson Capt, mi eles eo a Sens to understanding ow paw plabe dams chag their qoatve Sppenance ua parameter hang lee ae fw farther eps oft eyes Bxample 6.4.2 Vander Pols equation, Pe(2-1e t2=0, oy dsc a ulacr sel Gest that we wil tay utr ln Chapter SOvn ace HL cna be tard lata syst In the standard way See eo) nd the amocin pie plane droning aponts tn Figure 42 AL (Ce \& LX 2 ctr or Van er Pa uation ‘There certainly sens tobe lint eee in Figure 8.42, and his phe soeton an bo netod ae floes, We can think ofthe diferent ‘Sunn (0) Saering © damped harmonic oxator, th sion FT pat 2 Leon peste fr [a > yn oto words the coc Iatr i being en tht plaoment 2 ral nd damped or sowed ‘fie large Te not v0 mrpsing tt tse downto some partieaar 12 1 Sytem of Nome Deel Rauations 1 guite pombe to pros dicen exeations with eee ait cles The folowing om ase FIGURE 6.43. Sever inte or Beagle A. In Execs 8.4, you can poe tha the egaton has infiely my period soos, wth deren: tiptoe. ak “Tera many open poled! shou nk gk, oe nan, i caknovn how uty it rir ise eon #=Pla9) ¥ =a.) with gud payors Pandan ao In what conus Baier ie a * “Tare lor mij tren, te Puc Benison hore that ga colo teint on pe, Tete ee of eat eon 85 The Poincaré-Bendixson Theorem. A majo norm that guests the existence of Int cyl doe to Hen Poloaré enc) sad Bends (Sei ther feet uty. Tose astement and pot you soo read Sesion 6 5, ich ust requ Ue eso secton 9 Chapter. Hare we will ve 8 ‘ef and anpler spell caeof tha Plneare-Bendbon Theos tat (be tated flo fs 85. The Potnar-endase Theres, 13 ‘Theorem 84. (Poincaré-Bendisson Theorem, Annulis Form) LeL0 caf) < (0) be ow pre fnctionof pol x, continuous and cue diferente. Lat te the “ele” ion he plane gen Sn polr cordate by (8) | of) S75 8} soo] ° ten [Z] 40 in U, the mast contain ini pce of? = (9) "The hyphens (9) enn hat tho water fl ars zon the crn, sort poltng Inthe radial drei. Sooe th salar Product does nok ‘nit mut be postive o neato, acorn to whether he velar Tad virn eottrcocka or close. Without ls of generality, we ‘7 cue tt te ela pode (4) ee ‘Proof of Tasrem 85.1. Wel conde Uist a wraparound fan, ‘5 ey to aoc io Ua sine fae: onder te rei V= (0 |) << 60} 186 1 Sytem of Nonlinear Dif! Buatons ‘n-th (@,7)-pan as shown In Figure 85.2. FIGURE 85:2. Unerping ho ani is he Oran "The diferent eqution canbe weten i polar cowdinst sentra) alee), cd in Beample 841, by wetng nt, 20 Om yews fe a9) sd or hyptins (3) ips that (6) > On trogen Vs Then {he ajc wl ct the (lan, w th stone fhe ‘ommtion eo (Our hypothe imply that ie fant fr esaon (6), Maeve, the fiction G is petiole of period Br mith ramet 8, baths srk equation I ust what mar dace nt length Part Seton 8, Indulig the period mapping Ps) which ascites tore the salve of he soliton to egaton (98) wich passes Uno (hr) a @ =D ‘he intra J the masa ner osm Pi el, ou ee, 3 flO), 0) ace V ten fe nd P mae Fit tac, 45, The Poin endaon Theorem, 15 Ay consis mapping rom led and ound tara nt el ‘mint have ae point (Eserese 8651), Toe colton through this Bod ‘oi of enue, pari a = fant of 8, and the slain 1 x= Feo) te enn Eg (wth coming fcr caty "There «fs cvioas codon which plinth the eel in U | sige tbe ein VS fatal for equation (9), but is al ack ‘ttinna. Suppose sow tht ie aton, ddr 0, s tat sins © i pil, the Guvatve jr -< ~C forsee cnaane C'> 0. Tot fhe reson V,viewod at » Haceward animal, sols the alquenss ‘uation of Thom 47.5, 0 that te peo ution o (6) sigue, ‘nd comespondngly, te oqton (3) hee uagueeyl in U. "The conto ddr <0 ls oral qe die to wey sace @ esl» ompeated fein, bt ace nore nota cnion which Teds tote suse cond: If the diverge 2h , ate met le stsityoagmtve throughout U; thes thre a unique ce in U that ‘aac suo in U.Thi lor from he fat th rergroce ta voir Bold fn the plane muerte extent to whichis Dow 6 ‘entra dats aes cher wate to li pel, thereon bate them mold ave a sen preserved bythe or, hic contacts negate ‘vergence This lb coed Seton Sn hegre: ‘hen the dvergac rmgatie ete bc of Hae 8687 "For exalt tate the Pte Dandoon Them, me back to th imi ayer we be fart rover in Soon 84 ee Bxample 6.5.2. Conia the pte of difecatil qustins fom Exam OO ble[lee-aGh on ‘We etm othe cas when a= 1, ware weaken kno the wit eis ‘nit oye wooee hat an naan ono by aloud > Tand 2 ‘es ofracarr <1 il east the conditions ofthe Plneré Bandon ‘Theorem 85.1, ova in Figue 833, 16 8 Systems of Nonlinear Dieta Reations RY [SS FLOURE 853, A Psa Denon mms the nt lo? MP -phye style eh oworr he So fact about the Poincaré-Bendson Thorens hati does oo eal us bow tofu a sutable ans a dor to Koo ‘where to lok fo kn ye, Tat afte ute if, event soe ‘whze we ony an an lin ple ‘Example 65.3. Returning to the Van der Pl equsion (1) o (32) of ‘ample 842, sft car how to ie an sno the it elev ty afr yo esd on! ‘Nha prea te dena spprosiate sul tou ene lpi ef lope marks (an option the oeMath progam Dif Phase ‘Plane), Figure .Ashows on graph ell: only wae ‘ho moray slaps coming te verte ha proper destin. "igwe 8. Isa moo cranand anna fr the une roe, fr whieh ‘sual equations ean bet. We lav the wig the eons at rere 854 Hving the hue hat the nnscgh earves drown 0 the ‘igure ae the tots fr xr ope i hn wet ld FIGURE 8. A sts Psat Denon ana forthe i yo FeedetenO 105 8. Sytem of Noten Diftenia Egtons 8.6 Symmetries and Volume-Preserving Equations fora yer vstor Bald 1 ee serous ate Ua seo sae, sade o soares, ll sltins are tract fac y sinks and strc limit = ‘es, and backwards ty sources un repeling Hat eye, exp foe ‘eptrasces edn oyle tance However, duet equation at you study wil often sot be "geal" In esse and wil pia quite iret avo. Thi etal fot ‘nw of bah ofthe wo foliwing resenns (0) The vector ald my hve symmetries, eu rape 8.6.1. (U) Mee veto ld may boar presen. Soe Example 862. Brample 86.1. Consider thewyten Payee toy Yarra? ‘The compote shows the pcre in Fue 86.1 fr the pha pase FIGURE 63. Pas plane ora = ya bana =e bat 1 oppurs in Figure 651 that thre i's eoninous fay of load curve rounding the origin. Why sould they be thre? A carl lok tthe plctre appears to how tat the agra met rod tbe Haw-r+y = 0. This yin fat, tve and eay to show, a allows "Ton syameiy around the ine = +y 0 en by (9) (-ah 3). (One way of eresing the spate ito say tat f(a) (asain 6. Symmetries and Volume Preserving Bqatons 160 of theft! equation, then (—o(-f),~u(-f) a ashton 86 you an vey. This slut flows the spmunat jetry, but with te "Toe symmetry expaas the observed Dvr a flows: ston (clthy(e) cess the ne at y = Oak sae te fp ~ ya gain at Se tine then betwen tie and ne t+ we wl hve (llo+9lta +9) = (ule -2tte-9), ‘sac Uh slain ofthe diferent equation with the enc nil ‘roto. But this ston retams to the pot whee we sated, gi fag eto erode slaon. Ths, thee wil be continous fay af ‘erode wton fortis nian. A ‘Bxample 8.6.2. Consider th tem of cient! equations 2 ~2ox(e +29) asnlay) = conte +29) 4+ veal), "Tha compute owe the petra Figure 86.2 far the poe plane FIGURE 6.2. Phae pane fr 2 = 2nls+29)— xa), ¥ 2) +e). ele In Figure 862, wo oo» lots of thing that are not expecta fais, of poe slates and eparatrow of sud ling to ther ene. “Yet there dos not enon to be aay symmetry to expan thee unas phenomena in the previo ample. a vm 1. Sysen of None Dieta Equations “Toe dirt equation of Beample 62 espacial bce aren sresereing, Thi i an portast notion in al, whch we 9 expe, {ng the ction of flows rm Scion 8 Deinition 8.6.3. ‘heen equation x! = fx) in" with How 15 wlunepesroag (represeving ifn = 2) Ife ay suet U of Sul any th dimen vlame m-vlume( (0) = nvotume(0). ‘This is vil an important popety that difisentilogaton might hve, but i aot obvious that thee fe any easy way to cok water {he equation bathe property nat. Ae Carly 848 wl sow, sothing ‘onl be snl Real em eels, o simply die, 2h 4 Bla Ba tet Bey ave + ‘Beample 86.4 The diverges of the vector Sd fn Harpe. ai a 5 Ruresms Zcaraty)nttytetaaaet. ‘The dveenoe ofthe vector Bl in rape 8. is a a Fe Pele 29) — naan) (eke +5) ysl) =O. a "The roof the dvergnoce ie argly epliod by the allowing there ‘Theorem 8.65. Gicen «diferent suation = f(x), the deegece of f menares the rte of change ofsolumes under the flow dy Le for DER, we hove Soueds ge fart de ‘Proof sng the notation of xymptele expansion (Prt, Anpeni A), Ce] (re “i un(t2), - sas (Hnys oes) +(x) +t) 26 0, sine es a oot of te. wba (9 ‘olution te Ue diferent equation, Note Ta ottian ot) mean, ace 150, tar of tly ghar dor has Symmatros and Volume Presring Batons m ‘We tart witha frm rom Append Ls be, Oe Folin ate vl) a, [PaO olen Jigen ee ea ou jon, Olden ‘Wo cun so eh ac hat tug ay ef OhdOae) ea), was aet)= {1 Hogleatess ray 65, Bh tn trot she Pu/00, v0 Ble a tae ct Pus Olen Diente re with respec to and emtuating at = Oi the deste rel Cally 88 The Afr tion! = Ga i rou Th ints Tne 4 helt at Symp desc a eg Feber on Seatoaeva, = Stomatol ‘Since heen io ny dora Vn partial, V = 7) the ‘rove the dervatv ofthe volume oboe emstat the divergence ‘the vor Sed vanes, me preseng OF cours, volume preserving vctor fk cannot have any cores oF sina sae a ughborod oft ik mou be upped sly ide el ‘der the fom, ora oeghborood of a sure wool be mapped tly ‘msde fin eer ae, ele woul st be peer “his an az be ssn fom the lneariaton: fu! = wth aie ‘lon ofthe difaentis eqantion = (x) at ero x, then Bares 8.689 (Sts you to so Ai 00) = te, {tho vrtor ol is volume preserving, we mast oe son n= ths ipl hat ll ros sabe centers Gather speci) ‘ales ny, fom Theres 86.5 wes that m 8 Syst of Nonlinear Dies! uations +e ow a vlume expanding It A> 0 the fw is vole sinking tr A <0 ‘This eoe a lang may trad exphning why sure anit A> Oa snk aty eae allthis orp reserving al noms a itl mytrouy, ay ome e/a surpe chat a the two-dimensional cas, the rub jee as aly femal way bask fn Part 1, Chapt’, More speacaly, Ue sytan of sustins Fa fen) yaien = sae evga enon as as ay oo inexact, We nin ection 26 i Part Lon exc ferential equations how to‘conseue on any rcangle whee both and ae deel scion [Pg) wich constant on hulls of (8), Le, on the aoe at (Ge) "This aeate you can atl option fr the trae, alaing 2a y (sual imply. aap 88.7. n Heal 862; he fon Fs) (Snap) cen on te tet “TE mcaly cally spn bed Dba. Sah ae gn Fi ba ni mn ee posi apes mene jictcdenooa tn yun oer vasa re aise Ge ae Sto so ced i nds acre ie at {SS to goto one’ ah ete lvl or cea ol, motto niny (e+) + ‘This (sos) compselydomystien are praerving dierent equ ‘oti they are all obi by tang fncton Fe, 9) and stig oF % OF ooo Sich equine a ale Hemitonian in two dimensions thir oy it Sipe the faction Fis tant on trajectories, hich completly deta inne them. Thee Hanitoninn equations are central i pyeoeIn ghar ‘menins, one fncion lone doesnt deteloe cure, aod wo Wl ‘vin Cpr Il (in Pr i), Hatonian eantion are vary elaberate [a higher dimensions 86 Symmes nd Vote Preeving Batons im Foran ace pesrving dilrentilequntion, we ean redex soliton tolerating and mrtg fanesone, a at pile (0) Fit (as explain in Seton 26 In Pat Ton exe directs equations) the nein F sac at or, oF Bah Fas (Pt Fw a he Hit tion Cat 1 Pa (2) Next conser the equation F(z) = Cy a expresing y imply sn fein of y= #2). Nov: Song or derstanding he ‘ure y= (=) maybe iin prt. (9) Now the fst eqation booms separa, de f(o, 22) = tad ‘Hi ponbl to intra de/(e, 9(2) you can fd an xpreon Ge) eC. The neon Cl end tobe inva pes "The “alos” ineted inthe sentence about dentition comes foun ‘the ct that he eqution i defined on dma th hol the con FF tay fl tobe dele a he ene oan: Ths diel important, ‘ate wll nto hee. ‘Example 8.6.8 Consider the dirt equation fom Seton 65, vey ¥ ling the pend, or mote eel e ya ‘Tha equation often had continous alas of dosed trajectai, and eddie contetons, Wo can sow cl ee why () Thay sce eymmetsi with pect to the ni, which you can se tithe dey orm the vous symetry ofthe Hanan ante shen V(s) yeaa, (W) Ty ae sr preeving, nd infact, he Hamiltonian feo e Foss) =VA+VE), mm 8 Syston of Nonlinear Dial Equations ‘ko cal tho total enor. Note the very important fc that conservation ‘energy and commen of ae ae te ute ting in hi tak ‘You might wonder Js by looking at to phase plane o irate ‘ution, joa ean tll whee the egaton i valmmprencving Inthe Inge (lol), you may gt bine thot this 0 fom tho pte plane ‘proses of cara lames of pro sation nd of cotar Inthe lf you avs or sores, canbe Sure ot ee presrving Bit locally and sway fm ros you camot inte abwncs of els, gy patter of walter socal compatible withthe propa of blog Mare spately, von any vstor fold €on argon of tho plane wth se tech faricrmcre do aot wan in hn ein, ie there Function Jy) > O suc tat tho vctor Bld fs won psig. Tis ‘ata tat locally away fom sero) you eat adjust the lng of the ‘tors fran the actor elo ake sex reserving ‘Suck a finetion, wach acts abo muir on the vtrs ele cle as fuga factor and a sana Bare of elanetary courses (ern! equations. In mat cam, iia jst as hard to Bo a tearing fcr as to solve the equation, 0 we wll ot expand on this toe 8.7 Chaos in Higher Dimensions ‘Toe theory throughout Chapier, expecially in Sections 8.5 and 8. quite spect othe plane. Althoogh the a pneralizalions to hight ‘Season, sheave mach weaker ther bexnne the Bypoties 0 ‘don sated ce esas the cooclisions do ot desert ow wth ay Precision. In thi oton, we wan! to ge some explo tha rig ot the dil xample 87-1, Welruly encountered the Loens equi is Example (16, Rocl che following rather ance king astonor aca ins e=oy-2) Ynoeny—ae an po ie tey, ere pound thee equations ata reduction to tres dimensions of sot of prt eternal equations Jcebing ld convection: inthis ‘aw ib parameters ory and Baral pave: We wl oly comer the scpatien in he range £47. Chuo in Higher Dimensions 1 Sutin of the Loree equation the trina parte ae” = 10,9 ~ 8/3, and p~ 28 ae rprscted In Fique 87.1 1s much fase ogi ol be ths gure by Sag i move os compatr sare (Gea vides) han by looking mt tate pitas. Siow 27230 Syrat > Saye Sow Oi rd to show at wht slut) ‘the wajetrcs cane fo sil. (©) Conte iy letra ekition the mae of wich you expect ‘he palo ce ub] {8.1412, Suppor tat?) dees th postion of partie moving In ‘oe mension, under the potential V(a) Show thas the vetor eld in the plane corespending to syst, as described ia Section 5, has & 0 at (ent) Hand only fa datz) © and yy = 0 Show that at Sich» asthe Hoesen cote sf €°V/ds"oq) > 0, ba I the teal bas a nondepsntste minim. Show that tbe poeta ha 8 oodngroerate aun the Lnsaration bas ase i 8 Systems of Nonlinear Dies! Byatons Exercises 8.2-8.3. Saddles, Sinks, Sources 8-84. Fr ocate any sinks and bares 82-6442. Conary ferential eantions ® (©) Stow that oe of hee snglr points for () isd pint. Fin the igaretar directions (©) We have shown that the shaded region U in Figure 83.2, U=tlenl-1<2<0-8 0, by oem LE, tee exits as ‘Wayne eC RY such tbr In that bass A i epebioruppertangular TEL iatnc of abate vale 0, the xy a ink fo bn difretil uation. 8.28.40" Coser he diewaial equation =-08+ Ple.0) v= -ey + Qe), where « > 0, and P and Q start with quadratic vrs. Show that the ‘elon trated to the sin (0,0) at epi sound the re in: Pas to pear cnr, tnd wie an atin (2 ate woof of Tren 8.210. Us th fet that the slo ae atracel net ft othe cgi to stow that hee 2 > 0 and P and Q start with quartic tems. Sow that tbe ‘oloas attracted to the sk 0,0 do not eal and te orn. Hin: Conde the eset deena anton show cot tis wl deine in the reglon —8 Oy al ations Oy whe) he stn eo 5.042, Show that [Jeol Gre an explo an anal nit yle that sale on onside, ua aha th oh ‘8.4if9°, For the equation of Example 843, [ET -[n]+e+reats (i: ee py ee Exercises 8.5 Poinearé-Bendixson Theorem .5j1". Let I~ (a) be coed an bounded interval. Show thet ny ‘enuoacie mapping #1 {hazed pint Hat: Use ener ‘aloe teem, ppd to te faeton J) ~ 1.592. Coder the oqton of Beample 64.) and Figwe 843, b= Leer wali] 7 | | | | | | + 1 Berit wr (6) Draw aphac portrait and makes Poncrt-Bendicnn annus round coe of the get int eee. (0) Pind eto fran annie you foun in pst ‘5595. For thereat equation iT -[sa7]- gt pe pot ed yo de Pete ex and ‘cb ney 2.4", Conder the Van der Pol equation of Examples 42 and 85 Fl atin fhe a do we 635, i ped of stag ine pls iy porto ofthe woes of 0 £55, Show tht he vation = [andy 2] +e +G- C4949 [3] an in rin spat satis of Exercises 8.6 Symmetries; Area-Preserving Equations ‘861°. Consider the stu of dierent equasions (T-[3] Ce ae cartes aaah oe (©) tap (0, you sald have founda eo apparently Bs by ela, ‘Show that ths in fat te ae 18 {8 Syetems of Nonlin Dili Equations (@) To sada apparent ha a bootie separts (an unstable sp- ‘Sa hat cuves sound ad Teton the ala ar» stable sep ‘Sasa Show tht th the ee, and, far thi proble, that yoa ‘find en equation forthe parr 8.02, Code the set of deena gant [FT -[Seteu] (9 pea ing ern emp ge) em sigermes pee (6) pare (a), you should have found reyon apparel fil by eyes Sh tha ti sin fate ee. ‘Th remainder of tho oxrie attempts to oat thi region with gree (@) Consider the coeponiing cyt of unions dys. Show that theregon ei/2- Izy 4/2 ¢> lian safuane or ‘ apropit y Show thts etna soles the usquenes ‘property (6) Shack the ation ia he pfu (©) Show that al solani the pact of the ple Bounded by this solution we eae. S05". Iw’ = Au i the lnaraton of the diferent equation Aa) at 6 2r0 x, show that ‘844, Show hat lar diferent quaion = Ae ree peering fan ely ite A= ‘8.695. Draw phase porte foreach of the flowing dient equ ton (and prove) wher eit proprio symmatit oat Go) 2 teinee +220 © []-[2] +e +r sts [}] © [i] -[- eed] (re3] ‘is aruprrviog (ce Execs 6.63), thon es 2ros cannot be inks or ose (and Warr mist centr sad). BO#T. Let be wets ld delle In 9 rion 7 CRP. Show that thesia equntion x = fs) camot hove two cel, which ogee ‘oud argon Ve U in which dv P< 0. Exercises 8.7 Chaos in Higher Dimensions S.THP1 Show tha the dvereece othe vector Bat sy! ot: =|ecy-e “artes (241-46). Why she Lore equation a tobe diate? 8.72", Consider the function f(e,y3) = a + oy? +0(2 29). Toe ‘hj f ths eure eto hw tat thee a bounded regan (i fas, ‘ellpeold) which slant tha Laren eatin (i) eater at never (6) Show tnt he rgion f 20 8 Syste of Nonliner Dire Beuations (0) Show thatthe fnction fo + 92 432 ie 2 monotone decreasing fcr of tine when 0 p< ym hat ll goltions to the Lore ations (er tracted to res, (6) Sow sat the xg she only ao ofthe wor fil fo (8) fe bt tn there ze Ewer sero for > Ian give thle Coordinates (6) Stow tht thse new ano are inks for nd that they have one neaive genase and two complex cx {ate egevaans mith pole el pst for olos8+8) ares. (@) Show that the system of dforetial equations E]-Fe va sont eve os the did 2 +9 = 1,20 8 cere. (@) Compote the ston mapping Pang the section y = 0.3 > Oy ‘Sul show hat tthe xed pone of Pcomespoding the ce tht ‘Teitive of Phar two elgeals oe grater thn Tad oe ls (6) iad the sparc of heen point int sexton. (a) Dex the separation he ea, What bears in? do the partion separate Exercises 88, Structural Stability 8.891", Comlder the ten of diferent] equations (i= [22224] = earles om (a) With Atectlth’s Dif Phase Plane ke and pit phase portata lor a = 3,0, -35, “10. To eaptre all You nad to so bounds oe 20'S 15, “10

    You might also like