4.1.2 MATLAB Functions >> format long >> T = [300 400 500]; >> density = [0.
616
0.525 0.457]; >> p = polyfit(T, density,2) >> d = polyval(p,350)
14.2 Newton Interpolating polynomial
9 Graphical depiction of linear interpolation. The shaded areas indicate the
similar triangles used to derive the Newton linear -interpolation formula [Eq.
(14.5)]. Figure 14.2
10 FDD = finite divided difference The second FDD
11 Two linear interpolations to estimate ln 2. Note how the smaller interval
provides a better estimate. Figure 14.3
13 Example 14.3 Problem : f(x) = ln x �x 1 = 1 f(x 1 ) =0 �x 2 = 4 f(x 2 ) =
1.386294 �x 3 = 6 f(x 3 ) = 1.791759 Solution : �b 1 = 0 �b 2 = (1.386294 � 0) /(4-
1) = 0.4620981 �b 3 = f 2 (x) = 0 + 0.4620981(x-1) � 0.0518731(x-1)(x-4) f 2 (x) =
0 + 0.4620981(x-1) � 0.0518731(x-1)(x-4)
14 The use of quadratic interpolation to estimate ln 2. The linear interpolation
from x = 1 to 4 is also included for comparison. Figure 14.4
15 Newton Interpolation ? Divided-difference table : Adding (3,14) and (4,22) <- a
1 <- a 2 <- a 3
16 Graphical depiction of the recursive nature of finite divided differences. This
representation is referred to as a divided difference table. Figure 14.5
17 Example 14.4 Problem : f(x) = ln x �x 1 = 1 f(x 1 ) =0 �x 2 = 4 f(x 2 ) =
1.386294 �x 3 = 6 f(x 3 ) = 1.791759 �x 4 = 5 f(x 4 ) = 1.609438 f 3 (x) = b1 +
b2(x-x1)+ b3(x-x1)(x-x2)+b4(x-x1)(x- x2)(x-x3) b3(x-x1)(x-x2)+b4(x-x1)(x- x2)(x-x3)
18 Solution : �b 1 = f(x 1 ) = 0 �b 2 = f[x 2, x 1 ] = (1.386294 � 0) /(4-1) =
0.4620981 �f[x 3,x 2 ] = (1.791759 � 1.386294) /(6-4) = 0.2027326 �f[x 4,x 3 ] =
(1.609438 � 1.791759) /(5-6) = 0.1823216 �b 3 = f[x 3,x 2,x 1 ] = (0.2027326 �
0.4620981) /(6-1) = -0.05187311 = -0.05187311 �f[x 4,x 3,x 2 ] = (0.1823216 �
0.2027326) /(5-4) = -0.02041100 = -0.02041100 �b 4 =f[x 4,x 3,x 2,x 1 ] = (-
0.02041100 + 0.05187311) /(5-1) = 0.007865529 = 0.007865529
19 f 3 (x) = 0 + 0.4620981(x-1) - 0.05187311(x-1)(x-4) - 0.05187311(x-1)(x-4) +
0.007865529(x-1)(x- 4)(x-6) + 0.007865529(x-1)(x- 4)(x-6)
20 function yint = Newtint(x,y,xx) % yint = Newtint(x,y,xx): % Newton
interpolation. Uses an (n - 1)-order Newton % interpolating polynomial based on n
data points (x, y) % to determine a value of the dependent variable (yint) % at a
given value of the independent variable, xx. % input: % x = independent variable %
y = dependent variable % xx = value of independent variable at which %
interpolation is calculated % output: % yint = interpolated value of dependent
variable
21 % compute the finite divided differences in the form of a % difference table n
= length(x); if length(y)~=n, error('x and y must be same length'); end b =
zeros(n,n); % assign dependent variables to the first column of b. b(:,1) = y(:); %
the (:) ensures that y is a column vector. for j = 2:n for i = 1:n-j+1 for i = 1:n-
j+1 b(i,j) = (b(i+1,j-1)-b(i,j-1))/(x(i+j-1)-x(i)); b(i,j) = (b(i+1,j-1)-b(i,j-1))/
(x(i+j-1)-x(i)); end endend % use the finite divided differences to interpolate xt
= 1; yint = b(1,1); for j = 1:n-1 xt = xt*(xx-x(j)); xt = xt*(xx-x(j)); yint =
yint+b(1,j+1)*xt; yint = yint+b(1,j+1)*xt;end
22 14.3 Lagrange Interpolating polynomial weight coefficients The first order
Lagrange interpolating polynomial Lagrange interpolating polynomial The n-th order
Lagrange interpolating polynomial Lagrange interpolating polynomial
23 The second order Lagrange interpolating polynomial Lagrange interpolating
polynomial
24 Example 14.5 Problem : Use a Lagrange interpolating polynomial of the first and
second order to evaluate the density of unused motor oil at T = 15 o C �x 1 = 0 f(x
1 ) = 3.85 �x 2 = 20 f(x 2 ) = 0.800 �x 3 = 40 f(x 3 ) = 0.212 Solution : First-
order at x=15: �f 1 (x)= Second-order : � f 2 (x)=
25 function yint = Lagrange(x,y,xx) % yint = Lagrange(x,y,xx): % Lagrange
interpolation. Uses an (n - 1)-order Lagrange % interpolating polynomial based on n
data points (x, y) % to determine a value of the dependent variable (yint) % at a
given value of the independent variable, xx. % input: % x = independent variable %
y = dependent variable % xx = value of independent variable at which the %
interpolation is calculated % output: % yint = interpolated value of dependent
variable 14.3.1 MATLAB M-file:Lagrange
26 n = length(x); if length(y)~=n, error('x and y must be same length'); end s =
0; for i = 1:n product = y(i); for j = 1:n if i ~= j product = product*(xx-x(j))/
(x(i)-x(j)); end s = s+product; end yint = s;
27 14.4 Inverse Interpolation (1,1) (3,3) (5,5) -> (?,2) Polynomial interpolation
�Determine (n-1)-th order polynomial p(x) �solve p(t) = 2 Ex : (2, 0.5),
(3,0.3333), and (4,0.25) �Find x so that f(x)=0.3 �f 2 (x) = 0.041667x 2 �
0.375x+1.08333 �Solve 0.3 = 0.041667x 2 � 0.375x+1.08333 for x �x = 5.704158 or
3.295842
28 Extrapolation is the process of estimating a value of f(x) that lies outside
the range of the known base points. 14.5.1 Extrapolation
29 Illustration of the possible divergence of an extrapolated prediction. The
extrapolation is based on fitting a parabola through the first three known points.
Figure 14.10
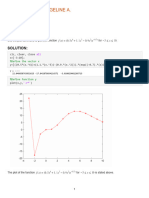
30 Example 14.6 Problem : Fit a seventh-order polynomial to the first 8 points
(1920 to 1990). Use it to compute the population in 2000 by extrapolationand
compare your prediction with the actual result. Solution : >> t = [1920 :10:1990];
>> t = [1920 :10:1990]; >> pop = [106.46 123.08 132.12 152.27 180.67 205.05 227.23
249.46]; >> pop = [106.46 123.08 132.12 152.27 180.67 205.05 227.23 249.46]; >> p =
polyfit(t, pop, 7) >> p = polyfit(t, pop, 7) Warning message �� Warning message ��
31 >> ts = (t-1955)/35; >> P = polyfit(ts, pop, 7); >> polyval(p, (2000-1955)/35)
>>tt=linspace(1920,2000); >>pp=polyval(p, (tt-1955)/35); Plot(t,pop, �o�, tt, pp)
32 Use of a seventh-order polynomial to make a prediction of U.S. population in
2000 based on data from 1920 through 1990. Figure 14.11
33 14.5.2 Oscillations Dangers of higher-order polynomial interpolation Ex :
Ringe�s function
34 Comparison of Runge�s function (dashed line) with a fourth-order polynomial fit
to 5 points sampled from the function. Figure 14.12
35 Comparison of Runge�s function (dashed line) with a tenth-order polynomial fit
to 11 points sampled from the function. Figure 14.13
