AoPS Community 1976 Euclid

Euclid Mathematics Contest 1976

www.artofproblemsolving.com/community/c854448
by dcouchman, WhizKid
– Part A

1 Source: 1976 Euclid Part A Problem 1

—–
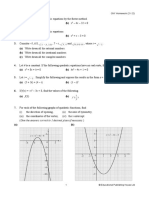
In the diagram, ABCD and EF GH are similar rectangles. DK : KC = 3 : 2. Then
rectangle ABCD : rectangle EF GH is equal to

A D

E K H

B F C G

(A) 3 : 2 (B) 9 : 4 (C) 5 : 2 (D) 25 : 4 (E) 6 : 2

2 Source: 1976 Euclid Part A Problem 2

—–
The sum of the series 2 + 5 + 8 + 11 + 14 + ... + 50 equals
(A) 90 (B) 425 (C) 416 (D) 442 (E) 495

3 Source: 1976 Euclid Part A Problem 3

—–
The minimum value of the function 2x2 + 6x + 7 is
5 9 9 5
(A) 7 (B) 2 (C) 4 (D) − 2 (E) 4

4 Source: 1976 Euclid Part A Problem 4

—–
The points (1, y1 ) and (−1, y2 ) lie on the curve y = px2 + qx + 5. If y1 + y2 = 14, then
the value of p is
(A) 2 (B) 7 (C) 5 (D) 2 − q (E) none of these

5 Source: 1976 Euclid Part A Problem 5

—–

© 2019 AoPS Incorporated 1

AoPS Community 1976 Euclid

If log8 m + log8 1
6 = 32 , then m equals
1 2 23
(A) 2 (B) 3 (C) 6 (D) 4 (E) 24

6 Source: 1976 Euclid Part A Problem 6

—–
4(x+3)(x−2)−24
The y-intercept of the graph of the function defined by y = (x+4) is

(A) − 24 (B) − 12 (C) 0 (D) − 4 (E) − 48

8 Source: 1976 Euclid Part A Problem 8

—–
Given that a, b, and c are the roots of the equation x3 − 3x2 + mx + 24 = 0, and that
−a and −b are the roots of the equation x2 + nx − 6 = 0, then the value of n is
(A) 1 (B) − 1 (C) 7 (D) − 7 (E) none of these

9 Source: 1976 Euclid Part A Problem 9

—– √ √
A circle has an inscribed triangle whose sides are 5 3, 10 3, and 15. The measure
of the angle subtended at the centre of the circle by the shortest side is
(A) 30 (B) 45 (C) 60 (D) 90 (E) none of these

10 Source: 1976 Euclid Part A Problem 10

—–
If f , g, h, and k are functions and a and b are numbers such that
f (x) = (x − 1)g(x) + 3 = (x + 1)h(x) + 1 = (x2 − 1)k(x) + ax + b for all x, then (a, b)
equals
(A) (−2, 1) (B) (−1, 2) (C) (1, 1) (D) (1, 2) (E) (2, 1)

– Part B

1 Source: 1976 Euclid Part B Problem 1

—– √
Triangle ABC has ∠B = 30◦ , AB = 150, and AC = 50 3. Determine the length of
BC.

2 Source: 1976 Euclid Part B Problem 2

—–
Given that x, y, and 2 are in geometric progression, and that x−1 , y −1 , and 9x−2 are in
are in arithmetic progression, then find the numerical value of xy.

© 2019 AoPS Incorporated 2

AoPS Community 1976 Euclid

3 Source: 1976 Euclid Part B Problem 3

—– I is the centre of the inscribed circle of 4ABC. AI meets the circumcircle of
4ABC at D. Prove that D is equidistant from I, B, and C.

4 Source: 1976 Euclid Part B Problem 4

—–
The remainder when f (x) = x5 − 2x4 + ax3 − x2 + bx − 2 is divided by x + 1 is −7.
When f (x) is divided by x − 2 the remainder is 32. Determine the remainder when
f (x) is divided by x − 1.

© 2019 AoPS Incorporated 3

Art of Problem Solving is an ACS WASC Accredited School.