Professional Documents
Culture Documents
Booklet of Nuclear PDF
Booklet of Nuclear PDF
Uploaded by
abdulbaseer0 ratings0% found this document useful (0 votes)
139 views100 pagesOriginal Title
booklet of nuclear.pdf
Copyright
© © All Rights Reserved
Available Formats
PDF or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
0 ratings0% found this document useful (0 votes)
139 views100 pagesBooklet of Nuclear PDF
Booklet of Nuclear PDF
Uploaded by
abdulbaseerCopyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
You are on page 1of 100
You might also like
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (844)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5814)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Audio RecDocument4 pagesAudio RecabdulbaseerNo ratings yet
- 5 BB 111 ChetryDocument17 pages5 BB 111 ChetryabdulbaseerNo ratings yet
- High Mass Star: Bs Physics 7th Semester Department of Physics Kohat University of Science and Technology, KohatDocument27 pagesHigh Mass Star: Bs Physics 7th Semester Department of Physics Kohat University of Science and Technology, KohatabdulbaseerNo ratings yet
- 1 PhysicdDocument8 pages1 PhysicdabdulbaseerNo ratings yet
- Cem 484 HW 1Document4 pagesCem 484 HW 1abdulbaseerNo ratings yet
- 157 PMDocument5 pages157 PMabdulbaseerNo ratings yet
- NEW5Document15 pagesNEW5abdulbaseerNo ratings yet
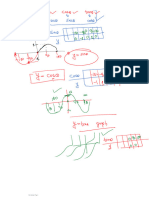
- Nuclear Physics: An OverviewDocument29 pagesNuclear Physics: An OverviewabdulbaseerNo ratings yet
- Found Errors in Solution? : Search More Solutions!Document3 pagesFound Errors in Solution? : Search More Solutions!abdulbaseerNo ratings yet
- Student Visa For Studies in Spain (For More Than 180 Days) : Embajada de España Islamabad PakistánDocument3 pagesStudent Visa For Studies in Spain (For More Than 180 Days) : Embajada de España Islamabad PakistánabdulbaseerNo ratings yet
- Scanned With CamscannerDocument6 pagesScanned With CamscannerabdulbaseerNo ratings yet
- L (20) Nuc-IIDocument11 pagesL (20) Nuc-IIabdulbaseerNo ratings yet
- N P Fermi-Gas ModelDocument8 pagesN P Fermi-Gas ModelabdulbaseerNo ratings yet
- List of Opportunities:: Summer Programs/InternshipsDocument7 pagesList of Opportunities:: Summer Programs/InternshipsabdulbaseerNo ratings yet
- Presented by Muhammad Bilal Khan MSC Physics Kust: Topic RadioactivityDocument28 pagesPresented by Muhammad Bilal Khan MSC Physics Kust: Topic RadioactivityabdulbaseerNo ratings yet
- Presented by Muhammad Bilal Khan MSC Physics Kust: Topic RadioactivityDocument28 pagesPresented by Muhammad Bilal Khan MSC Physics Kust: Topic RadioactivityabdulbaseerNo ratings yet
- Einstain Mistaks With e MCDocument4 pagesEinstain Mistaks With e MCabdulbaseerNo ratings yet
- L (12) Nuc-IIDocument10 pagesL (12) Nuc-IIabdulbaseerNo ratings yet
- L (18) Nuc-IIDocument13 pagesL (18) Nuc-IIabdulbaseerNo ratings yet
- Speed of Light Drops To Zero atDocument2 pagesSpeed of Light Drops To Zero atabdulbaseerNo ratings yet
- Measuring Quantum Geometries Via Quasi-Coherent States: MethodDocument2 pagesMeasuring Quantum Geometries Via Quasi-Coherent States: MethodabdulbaseerNo ratings yet
- L (17) Nuc-IIDocument11 pagesL (17) Nuc-IIabdulbaseer100% (1)
- General Relativity PDFDocument420 pagesGeneral Relativity PDFabdulbaseerNo ratings yet
- L (10) Nuc-IIDocument9 pagesL (10) Nuc-IIabdulbaseerNo ratings yet
- Complete Course ContantDocument17 pagesComplete Course ContantabdulbaseerNo ratings yet
- Complete Course ContantDocument193 pagesComplete Course ContantabdulbaseerNo ratings yet
- Social Welfare Services: The Basic Principles of Social WorkDocument1 pageSocial Welfare Services: The Basic Principles of Social WorkabdulbaseerNo ratings yet