HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

Chapter 2: Design of curved Beams

2.1. Introduction

Curved beams are used to support circular reservoirs, curved balconies and curved ramps, curved
girders. In curved beams the center of gravity of loads acting on a span lies outside the line
joining the supports. This causes the overturning of the beam unless it is fixed at supports or
continuous over supports. As the reactions and the loads do not lie along the axis at any point of
the beam, there will be torsional moment in addition to bending moment and shear force.

In case of circular beams supported by symmetrically placed columns the columns will give
vertical reaction. Due to symmetry the torsion at the center of curved beam between two
consecutive supports will be zero. Also, torsional moment at the support will be zero and there
will be only shear and bending moment at the supports.

The difference in analysis and design between the beams curved in plan and the straight beams is
mainly due to the presence of torsional moment induced by vertical load. Therefore, for such
members, it is necessary to design for internal bending moment, and twisting moment as well as
transverse shear.

Fig 2.1.

Chapter 2 Design of Curved Beams Page 1

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

The following sign conventions would be used for analysis.

Fig 2.2.

Example 1: A curved beam in the form of a quadrant of a circle of radius R and having a
uniform cross section is in a horizontal plane. It is fixed at A and free at B as shown below.
calculate and draw the bending moment, Twisting moment and shear force diagram for the
following two cases.

a) It is subjected to concentrated load P at the free end B.

b) It is subjected to a uniform load w per unit length
Solution:-
a) subjected to concentrated load P at the free end B.

Fig 2.3.

Take a point 'C' at as shown

ℎ = ( )

= = 0,⇒ = = = 90 ⇒ =

=− ∗ =− ( )

= = 0,⇒ =0 = = 90 ⇒ =−

=− ∗ = ∗ − ( ) =− (1 − ( ))

Chapter 2 Design of Curved Beams Page 2

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

= = 0,⇒ =− (1 − 1) = 0

= = 90 ⇒ =− (1 − 0) = −

The bending moment, Twisting moment and shear force diagram are shown below.

Fig 2.4.

b) subjected to uniform load w per unit length.

Consider any point x at an angle  from B as shown below.

Fig 2.5.

Shear force at section x is

ℎ , =
ℎ = 0, =0 ℎ = , = ∗ =
2 2 2
Bending moment at section x is
The bending moment due to uniform load will be negative since tension will occure at the top.
The bending moment due to uniform load on an element Rd at an angle from OX is given by

Chapter 2 Design of Curved Beams Page 3

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

=− ∅∗ ∅ =− ∅ ∅

= − ∅ ∅= ∅] = (cos( ) − cos(0)) = (cos( ) − 1)

ℎ = 0, = (cos(0) − 1) = 0
ℎ = /2, = (cos( /2) − 1) = −
Tiwisting moment at section x is
=− ∅ ∗ (1 − ∅)

=− (1 − ∅) ∅ = −[ (∅ − ∅)]

= − ( − )− (0 − 0) = − ( − )
ℎ = 0, =− (0 − (0)) = 0
ℎ = , =− ( /2 − ( /2)) = − ( /2 − 1) = −0.571
2
The shear force, bending and Twisting moment diagrams are shown below.

Fig 2.6.

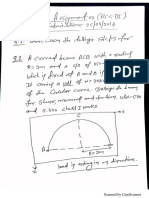
Example 3: A curved beam ACB with a radius of R=3m and a cross section of 450mmx300mm
which is fixed at A and B is shown below. It carries a uniformly distributed load of w=20 KN/m
length of the circular curve. Draw the bending moment and Twisting moment diagram and
design the beam for shear, moment and torsion. Use C-30 and S-420 class I works.

Fig 2.7.

Chapter 2 Design of Curved Beams Page 4

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

Solution:-
Vertical support reactions
ℎ =
The structure, loading and supports are symmetrical about OC.
Hence VA=VB
∗ ∗
2 = = = = = 94.25 Fig. 2.9
Because of symmetry the shear force and twisting moment at the midpoint C would be zero.
Consider a point P at angular distance with OC.

= − ∅∗ ∅

= − ∅ ∅= − (− ∅)

= + ( − 1)

= − ∅ ∗ (1 − ∅) = − (1 − ∅) ∅

= − [(∅ − ∅)] = − ( − )

We shall use the method of strain energy to solve for MC by the equation = 0 as there is no
relative moment between AC and CB. The strain energy is given by
/ /
∅
=2 +
2 2
/ /
= 2 + =0
2 2
/ /
= + ( )=0
2 2
2
= = ℎ =
2 2
2
= = ℎ =
2 2
/ /
=0 + ( )=0
2 2
/ /
+ =0

Chapter 2 Design of Curved Beams Page 5

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

/ ( / ( − ))
( + − 1)) ( −
+ =0
/ (cos )) / ( ))
( cos + − ( sin − − sin
+ =0
/ ( ) cos / ( ))
+ − ) ( + ) sin −
+ =0
1 + cos(2 ) 1 − cos(2 )
/ ( + )( )− ) / ( + )( )− ( ))
2 + 2 =0

1 sin(2 ) 1 sin(2 )
( + ) + − sin( ) + ( + ) − − (sin ( )
2 4 2 4

− cos( ) =0 ℎ =

( + ) − + ( + ) − =0
4 4
( + ) (1 + ) − (1 + ) = 0
4
( + ) =
4
4 4 4
( + )= = − = −1 = 0.273
= 0.273 ∗ 20 ∗ 3 = 49.14
Thus bending moment
2
ℎ = 0, = = 0+ ( 0 − 1) = = 49.14
2 2
ℎ = , = = = cos + cos −1 =
2 2 2
2 2
= = = 20 ∗ 3 = 180
Twisting moment
2
ℎ = 0, = = 0− (0 − 0) = 0
2
ℎ = , = = = sin − − sin
2 2 2 2
2
= = 49.14 ∗ 1 − 20 ∗ 3 − 1 = −53.6
2
Moment contra flexure point
2
= + ( − 1) = 0
20 ∗ 3
( + ) = ⇒ = = = 0.786
( + ) 49.14 + 20 ∗ 3
= cos (0.786) = 38.2
Point of Maximum span Twisting moment

= − ( − ) ; =0

= − (1 + )=0 ( + ) =

Chapter 2 Design of Curved Beams Page 6

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

20 ∗ 3
= cos ( ) = cos ( ) = 38.2
( + ) 49.14 + 20 ∗ 3
= sin(38.2) − 38.2 ∗ − sin(38.2)
180
= 87.36 sin(38.2) − 20 ∗ 4 ∗ 38.2 ∗ − sin(38.2) = 21.69
180

Fig 2.10
Design for flexure
= 0.85 ∗ = 0.85 ∗ .
= 13.6 /

24 /
= 0.21 ∗ = 0.21 ∗ = 1.165
1.5
At support = 180
Check the effective depth

180 ∗ 106
= = = 386.59
0.2952 0.2952 ∗ 13.6 ∗ 300
= 25 ,∅ = 10 ∅ = 20
∅ 20
= + +∅ + = 386.59 + 25 + 10 + = 431.59 ≤ = 450
2 2
20
= 450 − 25 − 10 − = 405
2
2 2 ∗ 180 ∗ 106 13.6
= 1− 1− = 1− 1− = 0.0119
2 2
300 ∗ 405 ∗ 13.6 365.22
= = 0.0119 ∗ 300 ∗ 405 = 1445.85
5∅20 , = 1570.8
At span = 49.14
20
= 450 − 25 − 10 − = 405
2
0.6 0.6
= = = 0.0014
420

Chapter 2 Design of Curved Beams Page 7

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

2 2 ∗ 49.14 ∗ 106 13.6

= 1− 1− = 1− 1− = 0.0028 ≥ … !
2
300 ∗ 4052 ∗ 13.6 365.22
= = 0.0028 ∗ 300 ∗ 405 = 340.2
2∅20 , = 628.32
Design for shear and Torsion: = = 94.25 = 53.6

From equivalent hollow section

450 ∗ 300
ℎ = = = 90
2(450 + 300)

= (450 − 90) ∗ (450 − 90) = 129600

= 2 (450 − 90) + (450 − 90) = 1440

Resistance of concrete to shear and torsion

= 1.2 ℎ = 1.2 ∗ 1.165 ∗ 129600 ∗ 90 ∗ 10 = 16.31

Vc = 0.25

= 1 + 50 = 1 + 50 ∗ 0.0119 = 1.595 ≤ 2

= 1.6 − = 1.6 − 0.405 = 1.195 ≥ 1

Vc = 0.25 ∗ 1.165 ∗ 1.595 ∗ 1.195 ∗ 300 ∗ 405 ∗ 10 = 67.45

Limiting or ultimate capacity of shear and torsion

Ultimate shear capacity (resistance)

V = 0.25 = 0.25 ∗ 13.6 ∗ 300 ∗ 405 ∗ 10 = 413.1

Ultimate Torsion resistance

= 0.80 ℎ = 0.8 ∗ 13.6 ∗ 129600 ∗ 90 ∗ 10 = 126.9

Reduction factor for ultimate (Limiting) shear and torsion strength

1 1
= = = 0.475
/ 53.6/126.9
1+( ) 1+( )
/ 94.25/413.1

1 1
= = = 0.88
/ 94.25/413.1
1+( ) 1+( )
/ 53.6/126.9

Reduction factor for concrete resistance to shear and torsion

Reduction factor for concrete strength

Chapter 2 Design of Curved Beams Page 8

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

1 1
= = = 0.39
/ 53.6/16.31
1+( ) 1+( )
/ 94.25/67.45

1 1
= = = 0.92
/ 94.25/67.45
1+( ) 1+( )
/ 53.6/16.31

After reduction factors

V′ = 0.475 ∗ 413.1 = 196.22 > = 94.25 −−− !

T′ = 0.88 ∗ 126.9 = 111.67 > = 53.6 −−− !

V ′ = 0.39 ∗ 67.45 = 26.31

T ′ = 0.92 ∗ 16.31 = 15.01

Effective Torsion to be resisted by reinforcement

T = T − T ′ = 53.6 − 15.01 = 38.59

Effective shear to be resisted by reinforcement

V = V − V ′ = 94.25 − 26.31 = 67.94

Longitudinal reinforcement for Torsion

38.59 ∗ 10 ∗ 1440
= = = 587.01
2∗ ∗ 2 ∗ 129600 ∗ 365.22

Provide 6∅12mm longitudinal bars , = 864

Stirrup reinforcement for Torsion assuming Φ10 stirrups are to be used

∗ 10 , 0.4 0.4 ∗ 300

= = 50.27 , = = = 0.3
4 400

1440
= = = 180
8 8

38.59 ∗ 10
= = = 0.41 /
2∗ ∗ 2 ∗ 129600 ∗ 365.22

Stirrup reinforcement for shear

0.4 0.4 ∗ 300

= = = 0.3
400

Chapter 2 Design of Curved Beams Page 9

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

Vs 67.94 ∗ 10
Vs = ⇒ = = = 0.46 /
365.22 ∗ 405

Total stirrups required for combined effect of Torsion and shear

2∗ ∗ 10
2 10 = = 157.08
4

= +2 = 0.46 + 2 ∗ 0.41 = 1.28 /

157.08
= = = 122.72 2 10 / 120 .
1.28 1.28

Example: Circular beam loaded uniformly and supported on symmetrically placed columns

Fig. 2.11

Consider portion AB of beam between two consecutive columns as shown above. Let the angle subtended
at the center by the two consecutive columns be . Because of symmetry, the torsion at each support is
zero. The load on this portion of beam would be:
= , ℎ ℎ
Let Mo be the support moments at A and B. The moment vectors Mo
at A and B are as shown below. Mo can be determined by
considering the moment equilibrium about line AB.
2 = 2∫ ∅ ∅−

Fig. 2.12
2 =2 ∅− ∅
2 2

2 =2 ∅−∅ =2 −
2 2 2 2 2

2 −
2 2 2
= = 1−
2 2 2
2

Chapter 2 Design of Curved Beams Page 10

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

To compute the bending moment and Twisting moment at any section in the beam, let us consider a
section X at an angle from OA.

= =
2

Fig 2.13

= − (1 − )+ ∅( − ∅)

= − ∗ (1 − )+ (1 − ∅) ∅
2

= − (1 − )+ (∅ − ∅)
2

= 1− − + +( − )
2 2 2 2

= − + −
2 2 2 2
=− + − ∅( ∅) = − + ∗ − ∅ ∅
2

=− + − ∅ ∅
2

=− 1− + + ( ∅)
2 2 2

= − 1− + +( − 1)
2 2 2

= + −1
2 2 2
Using the above equations, we can construct a table giving the critical values of the bending moments
and twisting moments and their positions. Bending and twisting moments of a circular beam supported on
N number of supports with:
360
= ∅ =
= , = , =

N a b c ∅
4 90 0.137 0.07 0.021 19 15′
6 60 0.089 0.045 0.009 12 45′
8 45 0.066 0.03 0.005 9 20′
10 36 0.054 0.023 0.003 7 30′

Chapter 2 Design of Curved Beams Page 11

 HAWASSA UNIERSITY INSTITUTE OF TECHNOLOGY SCHOOL OF CIVIL ENGINEERING

Fig 2.14.

Chapter 2 Design of Curved Beams Page 12