UNIVERSITI TEKNIKAL FAKULTI KEJURUTERAAN ELEKTRIK

MALAYSIA MELAKA
SUBJECT : BEKP 2453 ELECTROMAGNETIC THEORY

TUTORIAL 2

Gradient

1. Determine the gradient for the following scalar functions

a) S = 4 x 2 e − z + y 3
b) N = r 2 cos2 
c) M = R cos sin 

2. The gradient of a scalar function T is given by

T = zˆ e −2 z
If T = 0 at z = 0 , find T(z).

3. For the scalar function V = xy 2 − z 2 , determine its directional derivative along the direction of
vector A = xˆ − yˆ z and then evaluate it at P = (1, − 1, 4) .

Divergence

4. Vector field E is characterized by the following properties:

• E points along R̂ ;
• the magnitude of E is a function of only the distance from the origin;
• E vanishes at the origin, and;
•   E = 12 , everywhere,
Find an expression for E that satisfies these properties.

5. For the vector field E = xˆ xz − yˆ yz 2 − zˆ xy , verify the divergence theorem by computing:

a) The total outward flux flowing through the surface of a cube centered at the origin and with
sides equal to 2 units each and parallel to the Cartesian axis.
b) The integral of   E over the cube’s volume.

6. For the vector field E = rˆ10e − r − zˆ 3z , verify the divergence theorem for the cylindrical region
enclosed by r = 2, z = 0, and z = 4 .

ˆ 3R 2 , evaluate both sides of the divergence theorem for the region

7. For the vector field D = R
enclosed between the spherical shells defined by R = 1 and R = 2 .

Curl

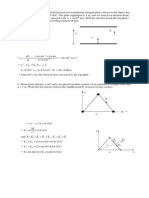
8. For the vector field E = xˆ xy − yˆ ( x 2 + 2 y 2 ) , calculate

a)  E  dl around the triangular contour shown in Figure Q8.
C

Tutorial 2 Sem 2-2019/2020 2BEKG Kyairul Azmi, Dr Fairul Azhar PAGE : - 1 -

 UNIVERSITI TEKNIKAL FAKULTI KEJURUTERAAN ELEKTRIK
MALAYSIA MELAKA
SUBJECT : BEKP 2453 ELECTROMAGNETIC THEORY

b)  (  E)  dS over the area of the triangle.

S

Figure Q8

9. Verify Stokes’s theorem for the vector field

B = rˆr cos + ˆ sin 
by evaluating
a)  B  dl over the semicircular contour shown in Figure Q9.
C

b)  (  B)  dS over the surface of the semicircle.

S

Figure Q9

ˆ cos + ˆ sin  by evaluating it on the

10. Verify Stokes’s theorem for the vector field A = R
hemisphere of unit radius.

Laplacian

11. Find the Laplacian of the following scalar functions:

a) V1 = 4 xy 2 z 3
b) V2 = 10r 3 sin 2
c) V3 = (2 / R 2 ) cos sin 

Tutorial 2 Sem 2-2019/2020 2BEKG Kyairul Azmi, Dr Fairul Azhar PAGE : - 2 -