Honors Precalculus Name More Linear Programming, Exponents, Logs and Partial Fraction Fun For questions 1~6, find the partial fraction decomposition (Calculator OK). 5, Lax? 4lx-7 x +8x +15For questions 7 ~ 12, graph the FUNctions and state the characteristics (No Calculator) [7 #(x)=27 32 +8. g(2)=log, (x+32)-2 9. h(x)=2 asymptote: y= — 32 [avmetote: = 32 [asmptote: y= —% _ domain (7, [ronge: (32,9 [soma (7) [ranges Cove) | domain (0,0) [ranae:(-#, 2) F()= ~ 1g fet (= 3 aoe 1(0)= at a casi Tim f(x)= im g(x) =dne fim A(x)= jo | tim W(x)= =8 | | | ! T | | 10. f (x) =—log, (x+8) 11. g(x)=-2"4 +64 12. h(x) = log, (64—x)—4 jsiseaee x= -& asymptote: = G4 asymptote: x = GY} domain: (-8, 9 [range:(-2/ | domain: (2/4 = (226) | domain: (4) | range: (—o,-) -3 | » 5 . 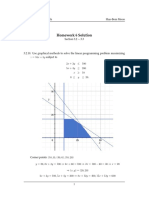2 A(x)=0, F(0)= -3 a= te | moe 2 | MO’ Jim f(z)=anc| im (x)=-c | lim e(=)= G4 | lime | Bim he) =dne Tt 1 | ' L 1 | |For questions 1316, solve the linear programming problem. 13. The liquid portion ofa diet isto provide at least 300 calories, 36 units of vitamin A, and 90 units of vitamin C daily. A ‘Cup of dietary drink X provides 60 calories, 12 units of vitamin A, and 10 units of vitamin C. A cup of dietary drink ¥ provides 60 calories, 6 units of vitamin A, and 30 units of vitamin C. Now, suppose that dietary drink X costs $0.12 per ‘cup and drink Y casts $0.15 per cup. How many cups of each drink should be consumed each day to minimize the cost and stil meet the stated daily requirements? yea yuchucs | C=0.12090" JA v= cupsey dank verve fcend Bly oo [eee wins Cost= 6.12% 40.(5y “y2e y20e ox + bay 2 30 IAx+ Gy 236 Jo + 3oy2 40 The minimum test 1s 10.66 when T dane Bugs of K ond Dcves of ¥ ao) 114. A merchant plans to sell two models of home computers at costs of $250 and $400, respectively. The $250 model yields a profit of $45 and the $400 model yelds a profit of $50. The merchant estimates thatthe total monthly demand will not exceed 250 units. Find the number of units of each model that should be stocked in order to maximize profit. Assume that the merchant does not want to invest more than $70,000 in computer inventory. fle x= cheep comoun> echoes | Prot Hons Sey Yo 4 2 expesiog Gore rae: Perbt= HSx4 Sey TS x20 420 xty £290 sox atcoy £74,00 # J lo, eo when AOU Cheap compu SO tkpersive15. A fruit grower has 150 acres of land availabe to raise two crops, Aand B. it takes one day to trim an acre of crop A ‘and two days to trim an acre of crop B, and there are 240 days per year available for trimming It takes 0.3 day to pick an ‘acre of crop A and 0.1 day to pick an acre of crop B, and there are 30 days per year available for picking. Find the ‘number of acres of each fruit that shokld be planted to maximize profit, assuming that the profit is $140 per acre for crop A and $235 per acre for crop B. Dax aeverog A Bey = eever 8 max Pohl = (Hox + d3Sy ‘ceo ure a okt xay £150 (os? The masimun @ d lun / 4,650 wl elxtdy S3Ho \ tS Rete \ =] A coop A © acces G.3x4 oly = 30 on ao acres of a crey B re plank 16. A farming cooperative mixes two brands of cattle feed. Brand X costs $25 per bag and contains 2 units of nutritional element A, 2 units of element B, and 2 units of element C. Brand ¥ costs $20 per bag and contains 1 unit of nutritional element A, 9 units of element 8, and 3 units of element C. Find the number of bags of each brand that should be mixed to produce a mixture having a minimum cost per bag. The minimum requirements of nutrients A, 8, and Care 12 units, 36 units, and 24 units, respectively. i verhues | Cort=aSy + Ry Seb xe bags Bed x SAS CT Bet = bess A Bred ¥ wins Cost = ISx+ dy x20 yee Ax rly 212 axty 236 dx 3y204 Ss The minimum cost ¢ is HAS when p