GRLWEAP 2010 Background

GRLWEAP 2010 Background Report
Table of Contents
1. PREFACE ............................................................................................... 1
1.1 History of the Wave Equation Approach ............................................ 1
1.2 Program History................................................................................. 1
1.3 What’s New in GRLWEAP 2010 ........................................................ 3
1.4 The Wave Equation Approach ........................................................... 5
2. BASIC CONSIDERATIONS AND APPLICATIONS OF THE WAVE
EQUATION .................................................................................................. 7
2.1 Energy Transfer ................................................................................. 7
2.2 Preparation for a Bearing Graph Analysis ....................................... 12
2.3 Preparation for a Driveability Analysis ............................................. 13
2.4 Interpretation of Wave Equation Results ......................................... 14
2.5 Checking Wave Equation Results ................................................... 15
3. THE WEAP ANALYSIS MODELS ......................................................... 17
3.1 Introduction ...................................................................................... 17
3.2 Hammer Details ............................................................................... 17
3.2.1 Working Principle of Liquid Injection Diesel Hammers .............. 17
3.2.2 Working Principle of Atomized Injection Diesel Hammers ......... 20
3.2.3 Working Principle of External Combustion Hammers ............... 20
3.2.4 Working Principle of Closed End or Double Acting Hammers ... 22
3.2.4.1 Closed End Diesel Hammers................................... 22
3.2.4.2 Double Acting External Combustion Hammers ...... 22
3.2.5 Drop Hammers .......................................................................... 23
3.2.6 Vibratory Hammers ................................................................... 25
3.2.6.1 Working Principle ................................................... 25
3.2.6.2 Limitations of Vibratory Hammer Analysis ............ 26
3.2.6.3 Preliminary Recommendations for Vibratory
Hammer Analyses ............................................................... 27
3.3 Basic Hammer Models..................................................................... 28
3.3.1 External Combustion Hammers ................................................ 29
3.3.1.1 The Ram of EC Hammers......................................... 29
Version 2010 GRLWEAP Procedures and Models i

3.3.1.2 Assembly of EC Hammers....................................... 29
3.3.2 Diesel Hammers ....................................................................... 32
3.3.3 Thermodynamic Models of Diesel Hammers ............................ 32
3.3.3.1 Liquid Fuel Injection (Impact Atomization) Model. 32
3.3.3.2 The Atomized Fuel Injection Model ....................... 36
3.3.4 Closed End Hammers (Double Acting) ..................................... 38
3.3.4.1 Double, Differential or Compound ECH ................. 38
3.3.4.2 Closed End Diesel Hammers ................................... 39
3.3.5 Vibratory Hammer Model .......................................................... 40
3.3.6 Hydroblok Hammers ................................................................. 41
3.3.7 Drop Hammers .......................................................................... 42
3.3.8 Hammer Energy Losses............................................................ 42
3.3.9 Inclined Pile Driving................................................................... 43
3.3.10 Driving at the Pile Bottom or at an Intermediate Pile Location 44
3.3.11 Static Soil Column Weight....................................................... 45
3.4 Driving System Model ...................................................................... 46
3.5 Pile Model ........................................................................................ 48
3.6 Splice/Slack Model .......................................................................... 50
3.7 Soil Model ........................................................................................ 51
3.7.1 The Basic Smith Static Resistance Model ................................. 51
3.7.2 Soil Damping............................................................................. 53
3.7.2.1 The Basic Smith Damping Model ............................ 53
3.7.2.2 Extensions to the Damping Model ......................... 54
3.7.2.3 Distribution of Shaft Damping............................. 55
3.7.2.4 Selection of Damping Factors ............................. 55
3.7.3 Soil Model Extensions ............................................................... 56
3.8 Numerical Procedure and Integration .............................................. 57
3.8.1 Time Increment ......................................................................... 57
3.8.2 Analysis Steps .......................................................................... 58
3.8.2.1 Prediction of Pile Variable at Time j ....................... 58
3.8.2.2 Forces at a Given Segment ..................................... 60
ii GRLWEAP Procedures and Models Version 2010

3.8.2.3 Newton's Second Law for Acceleration Calculation
............................................................................................. 61
3.8.2.4 Corrector Integration ............................................. 61
3.8.2.5 Further Iterations ................................................... 62
3.9 Stop Criteria..................................................................................... 62
3.10 Blow Count Computation - Non Residual Stress Analysis ............. 64
3.11 Residual Stress Analyses (RSA) ................................................... 64
3.11.1 Introduction ............................................................................. 64
3.11.2 Details of the GRLWEAP RSA Procedure .............................. 66
3.11.3 Additional Comments about RSA............................................ 68
3.11.4 RSA Restrictions ..................................................................... 69
3.12 GRLWEAP Analysis Options ......................................................... 69
3.12.1 Bearing Graph ......................................................................... 69
3.12.2 Inspector’s Chart: Blow Count vs. Stroke ................................ 69
3.12.3 Driveability Analysis ................................................................ 70
3.12.3.1 Gain/Loss Factors ................................................. 71
3.12.3.2 Variable Set-Up .................................................... 73
3.12.3.3 Notes and Hints on the Variable Set-Up Analysis 75
3.12.4 Second Pile Toe ...................................................................... 77
3.12.5 Two-Pile Analysis .................................................................... 77
3.13 Static Geotechnical Analysis ......................................................... 78
3.13.1 Introduction ............................................................................. 78
3.13.2 Soil Type Based Method (ST) ................................................. 78
3.13.3 SPT N-value Based Method (SA) ........................................... 80
3.13.4 The CPT Method in GRLWEAP .............................................. 83
3.13.4.1 Introduction ......................................................... 83
3.13.4.2 Data Import .......................................................... 83
3.13.4.3 Soil Classification .................................................. 85
3.13.4.4 Resistance calculation .......................................... 87
3.13.5 The API Method in GRLWEAP (Offshore Wave Version) ....... 88
3.13.6 Comments on GRLWEAP’s static formula methods ............... 89
Version 2010 GRLWEAP Procedures and Models iii

3.13.7 Consideration of Pile Inclination in Static Soil Analyses .......... 91
3.13.8 Static Bending Stress Calculation of Inclined Piles ................. 91
3.14 Program Flow ................................................................................ 94
3.14.1 Bearing Graph ......................................................................... 94
3.14.2 Driveability .............................................................................. 95
3.14.3 Inspector’s Chart ..................................................................... 97
3.14.4 Diesel Analysis Procedure ...................................................... 98
3.14.5 Vibratory Analysis Procedure .................................................. 99
4. INPUT INFORMATION ..................................................................... 101
4.1 Hammer Data ................................................................................ 101
4.2 Driving System Data ...................................................................... 101
4.3 Pile Data ........................................................................................ 102
4.4 Soil ................................................................................................ 105
4.5 Options .......................................................................................... 106
5. OUTPUT AND HELP INFORMATION ............................................. 111
5.1 Numerical Output........................................................................... 111
5.2 Bearing Graph ............................................................................... 112
5.3 Driveability ..................................................................................... 112
5.4 Variables vs. Time ......................................................................... 112
5.5 Stress Maxima Range Ouput for Fatigue Studies .......................... 113
5.6 Help ............................................................................................... 114
6. CONCLUSIONS AND RECOMMENDATIONS ................................ 117
APPENDIX A: CORRELATIONS ............................................................ 119
APPENDIX B: HAMMER MODEL DETAILS ........................................... 121
B1 Diesel Hammer Studies.................................................................. 121
B2 2002 Method for Diesel Hammer Pmax Calculation ......................... 121
B3 Measured Hammer Performance ................................................... 122
APPENDIX C: GRLWEAP FIRST STEPS .............................................. 125
Starting the Program ............................................................................ 125
Data Input ............................................................................................. 125
The Main Input Form ............................................................................ 126
Drop Down Menus ................................................................................ 126
EXAMPLE............................................................................................. 130
Appendix D: The GRLWEAP Friction Fatigue Approach .......................... 137
iv GRLWEAP Procedures and Models Version 2010

APPENDIX E: REFERENCES ................................................................ 146
Version 2010 GRLWEAP Procedures and Models v

vi GRLWEAP Procedures and Models Version 2010
1. PREFACE
1.1 History of the Wave Equation Approach
Since the early 1950's, when E.A.L. Smith introduced the wave equation
concept, this method of dynamic pile analysis has become increasingly
popular and its use widespread. Computer programs were prepared by
many private corporations as well as by the U.S. Department of
Transportation Federal Highway Administration (FHWA). The FHWA
supported work when both the Texas Transportation Institute (TTI) and the
WEAP programs were published (Hirsch, et al. (1976) and Goble, et al.
(1976)) and when the WEAP program was first updated (Goble, et al.
(1981)).
Throughout the development of this software package, PDI has strived to

keep the help files updated with the most recent hammer and driving
system information. This data has been submitted by hammer
manufacturers and equipment sales organizations. Preparation of this data
is a time-consuming effort and PDI gratefully acknowledges the effort made
by all contributors.
1.2 Program History
GRLWEAP developed out of the WEAP program of 1976. The original

WEAP had been written by GRL in cooperation with engineers of the FHWA
and the New York Department of Transportation. The software was
updated in 1981, and in 1986 a major rewriting was done which resulted in
WEAP86. WEAP86 also included the residual stress analysis of Hery
(1983) and was applicable to both mainframe and personal computers.
WEAP86 was further updated in 1987, resulting in a program nearly
identical with WEAP86. However, a new hammer data file, HAMMER.ALT,
was included in the package as part of an extensive study on diesel
hammer performance.
WEAP87 was developed, tested and documented under the sponsorship of

the Federal Highway Administration. Their contribution is gratefully
acknowledged. However, WEAP87 had to conform to certain limitations
making further developments difficult. For this reason, further program
developments, necessitated by industry developments, were made in the
GRLWEAP version.
The GRLWEAP package prior to 1993 consisted of several executable files

that had to be invoked by the user from the DOS prompt. The 1993 release
incorporated a shell program that provided a menu driven graphics
interface. This menu allowed for selection of input preparation,
modification, analysis, graphing, and program execution.
The 1998 Windows Version and the present version of GRLWEAP basically
follow the 1993 concept in that they divide the program into four distinctly
Version 2010 GRLWEAP Procedures and Models 1

different sections: Input, Analysis, Output and Hammer File Maintenance.
However, the program documentation was now contained in a single Report
Volume. The actual “User’s Manual” exists in the form of help files that are
released together with the program software. The novice may prefer to
generate a hard copy of these help files for ease of use.
The 2003-2005 versions included among others the following modifications:
 Two static analysis methods were added to simplify the input of

resistance distribution for bearing graph analyses and the shaft
resistance and end bearing input for Driveablity analyses. The soil
type based ST method allows for a simple analysis where only
basic soil information is available. Another method, the SA static
geotechnical analysis, uses SPT N–value input of soil resistance
for the Driveability analysis.
 Copy and paste features were added to Depth/Modifier Input Form

(D) and the Resistance Distribution Input Forms (S1 and S2) to
share information between GRLWEAP and other applications,
such as Excel.
 The hammer information was now organized in two separate

hammer database files: the PDI generated hammer file and a user
generated hammer file. This will prevent the user hammer
information from getting overwritten when PDI updates its hammer
files. Additionally, new hammer information was added to the
hammer database and to the drive system help. The hammer
efficiencies were also adjusted.
 Assembly Weight input was added to Hammer Override Dialog

box to allow easy override of assembly weight for external
combustion hammers. This is helpful, for example, when a
hammer model is available with different guides or sleeves which
add substantial weight to the hammer assembly and, therefore, the
static force of the hammer exerted on the soil. Gravitational
acceleration input for pile and hammer allow for modification of the
hammer and pile static weights to account, for example, for batter
and/or buoyancy.
 Rated and maximum diesel hammer stroke are distinguished. Diesel

iterations always start with the same initial stroke, rather than the
stroke from the previous analysis. Diesel hammer combustion
pressures were modified. For diesel hammers with very low soil
resistance values, the hammer may not run and such conditions
are now more clearly identified in the output.
 In the output programs the “Copy to Clipboard” command was added

to the “View” menu and variable times numerical output was
modified so that it can be saved to file and processed in other
programs.
2 GRLWEAP Procedures and Models Version 2010

1.3 What’s New in GRLWEAP 2010
This section lists the significant features that have been added recently to
the GRLWEAP program along with program enhancements. In addition to
these changes, PDI has been continuously updating the hammer data file
which along with update files can be downloaded from our website
(www.pile.com).
GRLWEAP’s 2010 program version comes in two modules, the standard

program and the “Offshore Wave”.
Standard program features now include:
For static geotechnical analysis in addition to the ST and SA methods:
(a) a CPT method for which the data has to be provided in the
form of a three column text file and
(b) a method based on API requirements.
For static geotechnical analysis, the SA method was modified as follows:
 In lieu of entering an SPT-N value, allow for an input of qu, the

unconfined compressive strength for clay and other cohesive
soils and allow for input of φ, the internal friction angle, for sand
and other cohesionless soils.
 The SPT-N value input is now completed in the main SA window

with automatic interpolation for each soil layer. Also the SPT-N
values for a certain layer will not be changed when a soil layer
depth is changed. A manually modified SPT-N value for a soil
layer will be maintained for a certain depth regardless of layer
 The graphics of the SA and ST input windows have been modified

now allowing for expansion by scrolling.
For the analysis of inclined (battered) pile driving:
 The program now allows entering the inclination degree or ratio.

The user then can accept/modify the suggested reduction factors
for hammer and pile weight, stroke reduction and efficiency.
 The graphics of the main input form shows the pile batter.
The Area Calculator now offers for pipe pile input of either outside
diameter and wall thickness or outside diameter and inside diameter.
Improvements related to Driveability analysis include:

 Most importantly: the end bearing input for driveability
analyses now has to be made as a unit resistance in the S1
form. It is very important to remember this change when
entering the soil resistance data.
 Also very important, in the S1 input form, a new column, Toe

Area, was added. This allows for a simplified data entry in
cases of soil plugging in certain layers.
 An automatic feature was added for generating an improved

Depth/Modifier table; this feature initializes the D-table based on
both the penetration entered in the main input form and the soil
layer information of the S1 table.
 The reset button in D-table input form has been improved to allow
users to reset depths considering both depth increment and soil
layers.
 After the S1-table has been complete, Gain/Loss factors are

initialized using the inverse of the maximum setup factor unless
they had been manually set before.
 The final penetration depth now can be modified in the main input
form (before it was inactive and showed the last depth entered in
the D-table). This penetration is now used to initialize the D-table.
For Inspector Chart analysis, the stroke increments were rounded off to
either 0.5 ft or 1 ft or 0.25 m or 0.5 m depending on the starting stroke
value.
In the Numerical Output, the format for SI output has been changed for
2
steel piles with a cross sectional area ≥ 1 m so that certain outputs will now
be shown in MN and MN/mm rather than kN and kN/mm. The bearing
graph output now includes additional information such as pressure (diesel),
coefficient of restitution of pile cushions (concrete piles) or hammer
cushions (steel piles), and capacity (Inspector’s Charts);
Allow to copy hammer/pile/soil model plot to other applications such as MS

Word.
The physical property table for pile, hammer cushion and pile cushion
material has been combined and updated.
A copy/paste feature has been added to the pile profile form (P1) to allow
creation/modification of pile input from other programs.
Changed pile strength/yield input to a critical section index for a simple

input of 0 for non-critical and 1 for critical sections.

Features available in the Offshore Wave Version:
 A Pipe Pile Builder for simplified input of complex pipe pile

sections and add-ons allowing for consideration of cut-off and
stabbing guide. In this case the graphical representation of the
model shows the stabbing guides instead of the solid area plot.
 Alternate hammer location at any point along the pile. The
related inputs are hammer location, hammer cushion stiffness and
helmet stiffness.
 Static bending analysis for inclined pile driving; related additional
input included: center of hammer gravity, hammer total weight,
jacket height and water depth; the latter two inputs are also shown
on the model plot. The output replaces the tension stresses with
the combined static bending and dynamic compression stresses.
 Fatigue Analysis tables are now an output based on a so-called
single blow approach. The tables include for each segment
maximum compressive and tensile stresses multiplied with the
number of their occurrences (from average blow count).
 Consideration of the Soil Column Weight in the static equilibrium
analysis which considers the help that the soil weight can add to
pile driveability.
 Friction Fatigue resistance distribution; this calculation is based
on the assumption that the shaft resistance near the pile does not
immediately lose resistance while the resistance some distance
above the toe reaches fully reduced values. .
1.4 The Wave Equation Approach
GRL's Wave Equation Analysis of Pile Driving is a program which simulates

motions and forces in a foundation pile when driven by either an impact
hammer or a vibratory hammer. The program computes the following:
 The blow count (number of hammer blows/unit length of

permanent set) of a pile under one or more assumed ultimate
resistance values and other dynamic soil resistance parameters,
given a hammer and driving system (helmet, hammer cushion, pile
cushion). For vibratory hammers the equivalent result is the time
required for a unit penetration.
 The axial stresses in a pile, both tension and compression,

averaged over the cross section for a certain pile penetration and
associated ultimate capacity values. In the offshore version certain
bending stresses are also considered.
 The energy transferred by the hammer to the pile for certain pile
penetration and associated capacity values.
 The pile velocity and displacements along the pile for certain pile
penetration and associated capacity values.

 The residual stresses remaining in the pile between hammer
blows.
Based on these results the following can be indirectly determined:
 The pile's bearing capacity at the time of driving or restriking,

given its observed penetration resistance (blow count).
 The stresses during pile driving, given an observed blow

count.
 The expected blow count if the static bearing capacity of the

pile is known (e.g., from a static soil analysis).
Of course, by varying the hammer type, driving system parameters

(cushions, helmet) and pile properties for a number of simulations, an
optimal system can be selected.
The present report does not replace previously published literature. Certain
basic features of wave equation programs will not be discussed. On the
other hand, this volume will elaborate on those details which experience
has shown to be the most difficult to comprehend. Among references useful
to the engineer involved in the analysis of impact pile driving are Smith
(1951 and 1960), describing the early wave equation approach, Samson et
al. (1963), Forehand and Reese (1964), Lowery et al. (1967) and Coyle et
al. (1973), as representative publications of the work performed at the TTI.
It should be pointed out that the thorough checking of the original 1976
WEAP code would not have been possible without the research work
performed at Case Institute of Technology (now known as the Case School
of Engineering at Case Western Reserve University) as reported by Goble,
et al. (1975). Additional developmental work conducted by the private
practice of the authors, as well as studies done by others, e.g. Blendy,
(1979), supplied the necessary correlation data. In addition, results from an
FHWA-sponsored study, "The Performance of Pile Driving Systems" by
Rausche, et al. (1985) were used in the development of WEAP. Other
relevant papers are referenced throughout this text and are listed in
Appendix E. Program performance has been evaluated by Thendean, et al.
(1996) and Rausche et al. (2004).

2. BASIC CONSIDERATIONS AND APPLICATIONS OF
THE WAVE EQUATION
2.1 Energy Transfer
The pile driving process readily provides information regarding the soil
resistance: the smaller the permanent set, s, of a pile under a hammer blow
with kinetic energy, Ek, the greater the soil resistance, Ru, which opposes
the pile penetration. This concept has been used for well over one hundred
years in the so-called dynamic or energy formulas, (the most commonly
used one in the U.S. is the Engineering News Formula). Note that Ek is the
kinetic energy of the ram immediately preceding ram impact and that R u is
the ultimate pile capacity, i.e., the maximum load that the pile can bear
before it experiences large settlement due to soil failure. Although
GRLWEAP does not directly work with an energy approach, these basic
principles still apply and should be discussed.
The concept of the dynamic formula is as follows:
Es = Ru s (2.1)
where Es is the energy available to do work on the soil and sl represents

losses in the soil, e.g. due to damping. The energy value, Es, is not simply
obtained from Ek. In general, the following energy balance is applicable:
Es = Ek - Eds - Epl - Esl (2.2)
In this equation Eds, Epl and Esl are quantities of energy lost in the driving
system, pile and soil, respectively. However, even E k is not readily known.
Generally, for modern hammers a "rated energy", Er, is given by the
manufacturer. Exceptions are hammers with internal impact velocity
measurement device which display on a control panel the energy of the ram
shortly before impact. Using the hammer efficiency, eh, one computes:
Ek = eh Er (2.3)
The hammer efficiency is a number between 0 and 1.
Modern hammers have an attachment called a helmet at the bottom of the

hammer, and one or two cushions. These and other devices make up the
components of the driving system. Energy, Eds, is lost in the driving
system and may be modeled with another loss factor called e d (see Figure
2.1). Then the kinetic energy available at the top of the pile is:
Ek - Eds = ed eh Er (2.4)
and the energy formula may be written as:
ed eh Er - Epl - Esl = Ru s (2.5)

Figure 2.1: Terminology and Energy Balance in the Hammer-Pile-Soil
System
Assuming Er to be known, an estimate of ed, eh, Epl, and Esl would yield the
permanent set, s, given Ru or vice versa Ru given s. The set, s, may be
computed from Ru before a pile is driven. The blow count, Bc, is the inverse
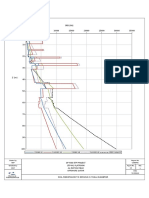
of s. Plotting the ultimate capacity vs. the blow count leads to the so-called
Bearing Graph. An example of two bearing graphs from different energy
formulas are shown in Figure 2.2.
Unfortunately, estimating the energy lost in pile and soil and estimating the
efficiencies of driving system and hammer are not easy tasks. The wave
equation approach differs from the energy formula primarily in the
evaluation of ed, Epl, and Esl. These losses are now computed by
mathematically modeling the driving system, pile, and soil. However, for

hammer losses, a hammer efficiency, e h, again is estimated based on
hammer type, hammer mode of operation and pile inclination (batter). This
estimate has been complicated by different hammer types and energy
definition. For example, the diesel hammer model calculates the energy
losses due to the precompression process, but uses an e h value (typically
0.8) to estimate all other losses (mainly friction) while hammers with internal
energy instrumentation are rated by the measured ram energy available just
before impact (eh is then often 0.95).
Bearing Graphs from Formulas
4500
4000
3500
Capacity in kN
3000
2500 Ru-Gates
2000 ENR - inferred
1500
1000
500
0
0 5 10 15 20
Blows /25 mm
Figure 2.2: Bearing graphs from two different dynamic formulas
For calculating the ed (losses in the driving system) effect, the wave
equation requires that stiffness values and coefficients of restitution of the
cushions and the weight of the helmet are known. For calculating E pl the
elastic modulus, length, specific weight of the pile and a coefficient of
restitution of the pile top are considered. The soil losses, E sl, are computed
by considering both a soil stiffness and a soil damping factor.
The computational procedure established by Smith again leads to a Bearing

Graph by calculation of the set s for an assumed or calculated ultimate
capacity value. In addition, tension and compression stress maxima can be
plotted vs. blow count.
The engineer may require that the pile be driven to a minimum blow count
taken from the Bearing Graph to assure that the corresponding minimum
ultimate capacity, Ru has been obtained. In this way, the wave equation
result is used to establish a driving criterion. On the other hand, during pile
driving the blow count, Bc, may be observed and Ru computed. This
process may be considered a dynamic pile test. However, it is not a very
thorough test because many analysis parameters have been estimated.
However, once a dynamic pile test has been conducted and the estimated
quantities have been verified, the resulting analysis is called a Refined
Wave Equation und its results are then more reliable.

For the inspector who in the field has to ascertain that the piles are driven to
the correct blow count, the task is complicated if the hammer cannot or
should not work
GRLatEngineers,
a constantInc.
stroke. For example, a hydraulic hammer can
and sometimesdemoshould
0.6mbe operated at different energy levels for reasons of
stroke GR
safety or expediency.35
In that case, for a desired end-of-drive
35
ultimate
capacity, the pile should be driven to blow counts which are higher for lower JUNTTAN HHK
hammer energies and lower for higher energies. This relationship can be
Compressive Stress (MPa) Capacity
Tension Stress (MPa)

readily prepared by28GRLWEAP in the so-called Inspector’s 28 Chart (Figure
Efficiency
2.3).
Helm et
A third situation is 21
also common. The engineer performs 21
as accurateHama m er Cus hio
static soil analysis as is possible, and plots the ultimate soil capacity asPile
a Cus hion
function of depth. 14 The wave equation is then used to 14 calculate the blow
Skin Quake
count for certain depth values and the input bearing capacity. In this way, Toe Quake
the blow count vs. depth curve is obtained. This process is called Skin a Dam ping
driveability analysis,7as it indicates the limits of an economical
7 Toe Dam ping
or safe pile
installation. Both Bearing Graph and Driveability analysis are very helpful Pile Length
for optimal driving system
0
selection. 0 Pile Penetration
Pile Top Area
1.50
Pile Model
Stroke in m
1.20
Stroke (m)
0.90
0.60
0.30
0.00
0 20 40 60 80 100 120 Res . Shaft =
Blow Count (blows /.25m ) (Proportional
Blow Count
Figure 2.3: Inspector’s Chart from GRLWEAP

Figure 2.4: GRLWEAP Driveability Result (Capacity and Blow Count vs
Depth)
In summary, the computational process in a wave equation is elaborately

compared to the simple dynamic formula, yet the wave equation still
requires assumptions and estimates of soil behavior, hammer efficiency,
and certain driving system parameters.
Finally, a word about the term "wave equation", this term refers to a partial
differential equation. Fortunately, it is unnecessary for the piling engineer to
solve this equation; this is done in an approximate manner by means of
Smith’s lumped mass model. However, the important contribution of Smith
was not solving the wave equation, but devising a complete analysis
procedure including recommendations for hammer, driving system, and pile
and soil parameters.
GRLWEAP has been expanded to include not only the basic wave equation
analysis but additional tools such static soils analyses and even a static pile
bending analysis for offshore piles. It is important to remember, however,
that these additional routines are only accessories to a dynamic analysis.
GRLWEAP has not been devised to design a pile. Its main task is to
calculate blow count and dynamic stresses given an assumed or calculated
ultimate bearing capacity value.

2.2 Preparation for a Bearing Graph Analysis
Before doing an analysis, prepare yourself by reading the relevant

information in Chapter 4 and in the on-line help section of the program (print
it out for convenience). Analyze the example cases. Submit to the
contractor and/or geotechnical engineer Form 1 of Chapter 4 (may be
printed for that purpose) for data collection.
The following steps are required for a standard analysis.
 Obtain a soil profile, including approximate soil strength values

such as standard penetration values, N. At least soil types and
densities or consistencies should be known.
 Establish a design (working) load, Qd, and a factor of safety (FS).

The factor of safety should reflect how well one knows the loads,
the soil properties, and the sensitivity of the structure to
settlements; also, the factor of safety should be greater the less
effort is made to determine the pile's bearing capacity. In general,
FS = 2 is only acceptable if more than just a wave equation is
done to ascertain pile bearing capacity. A Load Resistance Factor
Design (LRFD) approach (e.g. PDCA 2001) is preferable to the
allowable stress design procedure as LRFD considers of a variety
of uncertainties in the design and construction of driven piles.
 Compute the required ultimate pile capacity
Rur = Qd FS
Alternatively, for the LRFD approach, proceed as follows:
 Combine the various load components, Qi, multiplied by their

associated load factors, fi, to obtain the Factored Load.
 Determine the resistance factor, φ, as appropriate for the agreed

upon testing method and testing effort.
 Divide the Factored load by the resistance factor to determine the

required nominal load (which will be referred to as required ultimate
capacity in this document), Rur.
Rur = (1 / φ) Σfi Qi
Decide on a pile type.
 From static geotechnical analysis, establish the depth at which the

pile will most likely reach Rur and calculate the percentage and
distribution of the skin friction. If the soil strength changes due to
pile driving effects are known, determine the estimated amount of
skin friction and end bearing for both the end of driving and

restrike (after set-up) situations. It may be possible to drive the pile
only to Rur / fs, with fs being an overall setup factor which covers
capacity changes of both end bearing and shaft resistance. If the
soil loses strength during driving and then regains it after driving, fs
is greater than one. On the other hand, f s may be less than one in
the case of relaxation. Relaxation is a phenomenon which causes
the pile to lose strength after installation. In the troublesome case
of relaxation, the pile must be driven to a capacity in excess of Rur.
 Dynamic soil resistance parameters, damping, and quake may be

taken from the GRLWEAP help files for the given soil and pile
parameters, or they may be known from dynamic tests conducted
under similar circumstances.
 Select a hammer and driving system based on local availability.
 Submit all of this data for a wave equation analysis. Run the
analysis using Rur as well as other Ru values so that a curve can
be plotted with Ru being a function of the calculated blow count.
 Also plot the maximum tensile and compressive stresses, which

may occur at any location along the pile, as a function of blow
count.
2.3 Preparation for a Driveability Analysis
The following steps are required for a very basic driveability analysis.
 It is assumed that a geotechnical analysis has been performed

which established a required pile tip penetration. In that cases,
both unit shaft resistance and end bearing may be readily
available for input. If not, obtain reliable soil strength information
as an input to GRLWEAP and use SA, ST, API or CPT routines.
 For the soil types of the various layers, determine the appropriate
soil setup factors, fs (i.e., the factor with which the end of driving
capacity has to multiplied to find the long term pile capacity).
 In GRLWEAP enter the hammer, driving system and pile

information.
 In GRLWEAP enter the given unit shaft resistance and end

bearing directly into the S1 input form or choose from the four
different static analysis methods ST, SA, CPT or API to calculate
the unit soil resistance for all layers.
 In GRLWEAP decide on the Gain/Loss factors; usually one

chooses as the first shaft G/L factor the inverse of the highest
setup factor (Static Resistance to Driving, SRD) and as a second

one a factor 1.0 (representing the long term capacity). The G/L
values for the toe are normally left at 1.0.
 Complete the input and perform the analysis for various pile
penetrations.
 Two capacity vs depth relationships will be established (a) the low

resistance result which pertains to the continuous driving and thus
end-of-driving situation and (b) the high resistance analysis based
on the long term capacity which would be expected if major driving
interruptions occurred, e.g. after a waiting period during the
beginning of restrike testing.
2.4 Interpretation of Wave Equation Results
 Check the maximum pile stresses to see whether a safe pile

installation is possible.
 If the predicted blow count at Rur is excessive (e.g., greater than

100 blows/ft (330 blows/m or less than 3 mm set per blow) for
friction piles or 240 blows/ft (800 blows/m or less than 1.25 mm set
per blow) for end bearing piles, re-analyze with a more powerful
hammer. This more powerful hammer may have to be one with
more ram weight rather than drop height if stresses are high.
 If the predicted blow count at Rur is very low (e.g., less than 24
blows/ft (80 blows/m or greater than 12 mm set per blow),
construction control with a blow count driving criterion may be
inaccurate, and it is recommended to re-analyze with a reduced
hammer energy or a less powerful hammer.
 If blow count is acceptable but compressive stresses are

unacceptably high, re-analyze with either a smaller hammer,
decreased stroke or ram fall height (if hammer is adjustable), a
heavier hammer with less stroke or an increased cushion
thickness or a softer cushion material.
 If blow count is low, but tension stresses are too high for concrete
piles, either increase the pile cushion thickness, decrease the
stroke or use a hammer with a heavier ram and then re-analyze.
 If blow count is high and tension stresses are also too high for
concrete piles it may be necessary to choose a hammer with
greater ram weight and then re-analyze.
 If both blow count and stresses are excessive, increase pile cross
sectional area if possible or use a higher strength pile material and
then re-analyze.

2.5 Checking Wave Equation Results
There are many potential error sources. It is the engineer's duty to assure
that simulation and actual field conditions are in agreement.
 The first check must be on the actual pile size, length and material.
 Cushions and helmet must be checked in the field for size,

material type and condition. In particular, the pile cushion
thickness of concrete piles may vary.
 The hammer type must be checked and even though the data is
taken from the GRLWEAP hammer data file, the numerical output
must be checked to assure that the hammer data analyzed
corresponds to the system specified. Also, during driving it must
be confirmed that the hammer runs according to both the analysis
parameters and the manufacturer's specifications.
 In most cases, and always for high capacity piles or whenever

unusual driving conditions exist, dynamic measurements should
be taken during initial drive or restrike. Under certain
circumstances, a static load test may also be necessary.
1. If dynamic or static measurements have been taken under

comparable soil and pile conditions, re-analyze the situation to
learn about dynamic soil properties and use this information for a
refined wave equation analysis.
2. If dynamic measurements are available and have indicated a

hammer performance either better or not as favorable as
suggested by the “canned” GRLWEAP hammer models, be sure to
modify the input parameters (primarily the hammer efficiency)
accordingly. The hammer data file parameters represent average
hammer properties over all makes of the same hammer type.
These parameters do not represent the performance of a particular
product and cannot possibly reflect a certain state of maintenance.
3. The engineer must expect that the bearing capacity predictions

obtained from correlation between wave equation analyses and
actual pile driving blow counts will differ from static load test
results. In general, the finer the grain of the soil material, the larger
these differences can become. Correlation of wave equation
results with blow counts from restrike tests may reduce the
potential for inaccurate results. However, less than a 10 percent
difference can never be expected, since even measurements and
interpretations of static load tests are subject to errors or
differences of such magnitude.

3. THE WEAP ANALYSIS MODELS
3.1 Introduction
After a short description of the construction and operation of commonly

encountered impact hammers, this chapter describes how GRLWEAP
represents the hammer components which are significant for the force,
momentum and energy transfer to the piles. The models of the driving
system, pile and soil also will be described.
3.2 Hammer Details
Impact pile driving hammers may be classified as follows:
 Diesel hammers with liquid injection

 Diesel hammers with atomized injection
 Open end diesel hammers
 Closed end diesel hammers
 Single acting air/steam/hydraulic hammers

 Double acting air/steam/hydraulic hammers
 Hydraulic drop hammers
 Hydraulic power assisted drop hammers
 Hydraulic hammers with internal energy measurements
 Drop hammers - free fall

 Drop hammers - brake released
 Vibratory hammers
All except the diesel and vibratory hammers are called external combustion
hammers. Their basic models are practically identical, however, their
efficiencies vary. Diesel hammers are Internal Combustion Hammers.
Normally hammers are thought to act at the pile top, however, certain
external combustion hammers can also drive a pile at an intermediate pile
point or at the bottom. The offshore version of GRLWEAP provides such a
feature as an option.
3.2.1 Working Principle of Liquid Injection Diesel Hammers
Diesel hammers operate on a two stroke engine cycle. Figure 3.2.1

illustrates the working principle of a liquid injection open end diesel.
The hammer is started by raising the ram with a lifting mechanism. At a

certain fall height, the lifting mechanism is tripped (Figure 3.2.1a), the ram
is released, and it descends under the action of gravity. When the ram
bottom passes the exhaust ports, a certain volume of air, V i, is trapped in
the cylinder, compressed, and therefore heated.

Figure 3.2.1: Working Principle of a Liquid Injection Open End Diesel
Hammer

 Sometime before impact, a certain amount of fuel is squirted into
the cylinder under relatively low pressure (Figure 3.2.1b).
 When the ram collides with the impact block (Figure 3.2.1c), the
trapped air is compressed to a final volume, V f, which is usually
equivalent to the volume of the hammer's combustion chamber.
The fuel is splattered by the impact into this combustion chamber,
and combusts after a short delay (Figure 3.2.1d).
 The so-called combustion delay is due to the time required for the
fuel to mix with the hot air and to ignite. More volatile fuels might
have a shorter combustion delay than heavier ones. Combustion
occurring before impact is called preignition (it can be modeled in
GRLWEAP with a negative combustion delay) and can be caused
by the wrong fuel type or an overheated hammer. In hard driving,
severe preignition is usually undesirable, as it may reduce the
velocity of the ram (and thus the ram’s energy) prior to and
cushioning the impact.
 After the fuel has begun to combust, it will be causing a quick

increase in the pressure of the chamber until, after the so-called
combustion duration, the maximum pressure, P max, is reached.
The maximum pressure is an important quantity because it
governs the achieved stroke height. The Pmax-value may be
measured on the hammer, however, the pressure values in the
GRLWEAP program have been back calculated in such a way that
the calculated stroke reaches the rated stroke under refusal
conditions (Appendix B2).
 During impact, the impact block, hammer cushion and pile top are
rapidly driven downward leaving the cylinder with no support and
letting it descend by gravity.
 Pile rebound and combustion pressure push the ram upwards.

When the exhaust ports are cleared, some of the combustion
products are exhausted leaving in the cylinder a volume, V i, of
burned gases at ambient pressure (Figure 3.2.1e). As the ram
continues to travel upwards, fresh air, drawn in through the
exhaust ports, mixes with the remaining burned gases (Figure
3.2.1f).
 Depending on the reaction of the pile and the energy provided by

combustion, the ram will rise to some height (stroke). It then
descends again under the action of gravity to start a new cycle.
While the ram moves upward or downward with the exhaust ports
open, the chamber is scavenged, and fresh air replaces the
burned gas.

3.2.2 Working Principle of Atomized Injection Diesel Hammers
This hammer type is started in a manner identical to the L.I. (Liquid

Injection) type. However, for the Atomized Injection (A.I.) hammer, the ram
descends to within a small distance of the impact block and only then is fuel
injected at high pressure. The high pressure injection causes the fuel to be
immediately atomized and mixed with the hot compressed air. Thus,
combustion starts shortly after injection, independent of impact. Injection
lasts until, some time after impact, the ram has traveled a certain distance
from the impact block. Note that since distances and thus volumes (or
sometimes associated pressures) govern the process, combustion start and
stop volumes can be identified. Furthermore, the time duration from the
start of combustion to its end depends on the speed of the ram. The higher
the ram speed, the shorter the time periods between ignition and impact
and between impact and the end of ignition and combustion. During the
time of combustion the pressure is assumed to be maintained at a constant
maximum value pmax which again is back calculated for the GRLWEAP
hammer data file based on the energy rating of the hammer (Appendix B).
3.2.3 Working Principle of External Combustion Hammers
Diesel hammers carry their own source of energy in a fuel tank attached
directly to the hammer. All other hammers utilize an external engine or
device to create mechanical energy. This energy is then transferred to the
hammer either by means of hoses carrying steam (steam hammer),
compressed air (air hammer), pressurized hydraulic fluid (hydraulic
hammer) or a hoist and rope (drop hammer).
For analysis purposes, it is only important to realize that immediately prior

to impact, the ram is descending at a certain speed. In some cases, the
action of the motive fluid may slow this descent and have a self cushioning
effect. This will occur if the fluid causes a lifting force on the ram before
impact. Generally, this pre-admission is an abnormal condition and occurs
only in hammers with incorrect valve settings. The situation cannot be
detected by simple inspection methods and, due to the large variety of
hammer designs, it cannot be simulated in GRLWEAP.
The equivalent to the diesel hammer's cylinder is the assembly of ECH

(External Combustion Hammers). The assembly is simply the entire
hammer, except for the ram and the attached piston rod and piston.
Typically, the assembly consists of a hammer base, ram guides, cylinder
and other hammer components of significant weight. Initially, the assembly
is supported by the helmet, and therefore, by the pile which in turn pre-
compresses the soil. As the ram impacts against the striker plate, hammer
cushion, helmet and pile, the assembly is momentarily unsupported and
starts to fall due to gravity. When the assembly reaches the helmet again,
a so-called assembly impact occurs which may create significant forces in
the pile, particularly if the pile and helmet sharply rebound from the initial
impact of the ram. Thus, because of the soil precompression and because
of the assembly impact forces, the assembly should also be included in the

hammer model. Figure 3.2.3 shows the working principle of a single acting
air/steam hammer as an illustration.
In recent years, several different types of hydraulic hammers have come

into use. Some of these units have stepless adjustable ram fall heights or
energy settings. Several hammer types are designed with true free falls;
others are double acting, but with internal ram speed monitoring. In general,
these hammers avoid by design the problem of preadmission.
Figure 3.2.3: Working Principle of a Single Acting Air/Steam Hammer

For most types of ECHs, the hammer potential energy is based on ram
stroke times ram weight plus a contribution from the downward pressure.
Impact velocity is then calculated from this energy rating under
consideration of the hammer efficiency which covers energy losses
occurring during the descent of the ram. As mentioned, several modern
hydraulic hammers have a built-in energy monitoring device that can
determine the kinetic energy just before impact. In this case, it is
unnecessary to calculate the impact velocity from potential ram energy and
an estimate of energy losses. The rating, in this case, reflects the impact
energy, and the hammer efficiency is therefore near unity. Note: it is
possible to equip practically all hammers with an impact measuring device,
a highly recommended measure if construction control relies on blow count.
3.2.4 Working Principle of Closed End or Double Acting Hammers
Closed end or double acting hammers operate at a higher blow rate than
open or single acting units. The higher frequency of impacts is
accomplished by the exertion of a downward force on the ram during its
descent. For closed end diesels, this force is passively created by air
trapped between the top of the ram and the closed cylinder top. For ECH
the ram stroke may be limited by either active (motive fluid) or passive
pressure.
3.2.4.1 Closed End Diesel Hammers
Closed end diesel hammers are very similar to open end diesels, except for
the addition of a Bounce Chamber at the top of the cylinder. The bounce
chamber has ports which, when open, allow the pressure inside the
chamber to equalize with atmospheric pressure. As the ram moves toward
the cylinder top, it passes these ports and closes them. Once these ports
are closed, the pressure in the bounce chamber increases rapidly, slows
the ram’s upward motion, and prevents a metal to metal impact between
ram and cylinder top. The bounce chamber pressure can only increase
until it is in balance with the weight of the cylinder, called the Reaction
Weight. If the ram still has an upwards velocity, uplift of the entire cylinder
will result. In the field, this uplifting cannot be tolerated as it can lead both to
an unstable driving condition and to the destruction of the hammer. For this
reason the fuel amount, and hence maximum combustion chamber
pressure, has to be reduced such that there is only a very slight "lift off" or
none at all. Figure 3.2.4.1 shows one particular type of closed end diesel
hammer in various phases of operation. In order to modify the ram
deceleration and acceleration over time, some closed end diesel models
have a compression tank added to the upper cylinder; the portion of the
cylinder between the tank ports and cylinder top is then referred to as a
Safety Chamber.
3.2.4.2 Double Acting External Combustion Hammers
The analysis of the ECH double acting hammer type does not significantly
differ from single acting units. In fact, for ECH, GRLWEAP works with an

equivalent stroke which is rated hammer energy divided by ram weight. It is,
therefore, immaterial in the analysis of a double acting ECH whether or not
the energy or impact velocity was attained by a downward pressure, free
fall, or other means. Prior to 1998 GRLWEAP modeled double acting ECH
with a rated pressure and the effective area over which this pressure works.
This option has been removed and the data file simplified to reduce the
possibility of errors due to confusion or lack of information.
For ECH the downward force on the ram is often created by active
pressure. In that case, under hard driving conditions, the hammer assembly
tends to uplift which leads to unstable driving conditions. The operator will
then reduce the pressure which in turn leads to a reduced impact energy.
This is the main reason why double acting air/steam/hydraulic hammers
have lower GRLWEAP efficiencies than their single acting counterparts.
For modern power assisted ECH with passive pressures above the ram
(similar to the compressed air above the piston of a closed-ended diesel
hammer), uplift is normally avoided and such hammers can therefore be
analyzed with higher efficiencies.
Traditional double acting air/steam hammers are designed with either the
truly double acting mechanism which maintains full active pressure
throughout the downstroke. The other system, the differential hammer, is
designed such that the initially full pressure expands and reduces during
the downstroke. The differential hammer uses less motive fluid; however,
either system achieves high blow rates such as 120 impacts per minute,
Rausche, et al., (1985). Obviously, for these hammers, exact valve timing
becomes even more important for full energy development than for single
acting hammers which run at half this rate.
Modern hydraulic hammers have been designed with a variety of other

power assisting mechanisms during the downstroke. For example, the IHC
hammers work with an adjustable downward directed nitrogen gas pressure
which can be used to adjust the hammer impact velocity and blow rate.
Other hydraulic hammers may use only a low pressure force that balances
other potential energy losses.
3.2.5 Drop Hammers
The classic drop hammer is lifted with a hoist and rope and then released.
If the ram is freely released (which is rarely the case), one can speak of a
free fall hammer. If, however, the ram is released by releasing the brake of
the hoist and letting the winch unspool, then significant losses of energy
must be expected due to rope friction and winch inertia and possible early
engaging of the brake by an operator who does not want to risk that the ram
falls off the pile after impact.

3.2.6 Vibratory Hammers
3.2.6.1 Working Principle
Figure 3.2.6.1 shows a sketch of a vibratory hammer. These hammers may

be powered either electrically or hydraulically, and both hoses and cables
are usually elastically connected to the hammer's bias weight (vibration
isolator or upper mass). Vibration is generated by pairs of rotating eccentric
masses which rotate in opposite direction such that their horizontal forces
cancel while their vertical forces superimpose. The drivers for these
eccentric masses are located in the oscillator part (motor or lower mass) of
the hammer, which is connected to the bias weight by means of springs
and/or shock absorbers. Typically, low frequency hammers rotate at
speeds of 10 to 40 revolutions per second (Hz). So-called resonance
hammers rotate at higher speeds. Of course, the number of revolutions per
second is equal to the hammer's vibratory frequency. The rotation of the
eccentric masses produces centrifugal forces which are transferred to the
pile through a "clamp", which is often remotely operated with hydraulic
power. It is necessary to make this hammer-pile connection rigid to avoid
destruction of the pile top. The maximum compressive or tensile forces
which the eccentric masses, me, with eccentric radius, re, produce at a given
frequency, fV, (in cycles per second or Hz) are given by:
2
FVX = me re (2π fV) (3.1)
Therefore, the variation of the vibratory force, F V, over time, t, has the form:
FV = FVX sin(2π fV t) (3.2)
Figure 3.2.6.1: Sketch of a Vibratory Hammer

The product mere is referred to as the eccentric moment of the hammer.
This moment is not necessarily constant for a particular hammer if the
hammer model allows for a variation of the mass by insertion or removal of
mass units. Furthermore, so-called resonance free hammers can vary the
eccentric moment during operation. This allows for starting the hammer at
low or zero eccentric moment until a high enough frequency is reached at
which soil resonance does not occur. The eccentric moment is then
increased as desirable. Vibrohammer manufacturers often specify the
eccentric moment, maximum frequency, and rated power or the required
power of the associated power pack. Also, a vibratory amplitude is often
specified. When only the eccentric moment is known then for sufficient
accuracy a reasonable eccentric radius can be assumed and the
corresponding mass calculated by dividing moment with radius.
In order to gain an understanding of the power transfer from hammer to

pile, it is helpful to consider two extreme situations. In the first, the pile is
light and has practically no soil resistance. The oscillator of the hammer
then vibrates freely at an amplitude which is governed by the mass of the
oscillator and frequency. Energy dissipation in this case occurs primarily in
the connection between bias weight and oscillator. In other words, the
hammer will run with very low power, practically transferring very little
power to the pile, while it penetrates into the ground. In the second extreme
(and physically impossible) case, the pile is held rigidly by the surrounding
soil. Then there is no motion associated with the vibratory forces which
means that no energy transfer occurs, and again the hammer cannot
deliver any power to the pile. It is therefore reasonable to expect that the
power requirements first increase and then decrease as soil resistance
increases.
3.2.6.2 Limitations of Vibratory Hammer Analysis
It is well recognized by the profession (see also Holeyman, 2002) that the
analysis of vibratory pile driving is difficult at best. The main reason is the
strong effect that vibratory pile motion has on the effective soil stresses and
thus the soil resistance. As a result, piles in cohesionless soils, in particular
those that are submerged, may lose up to 95% of their shaft resistance and
50% of their end bearing. On the other hand, for cohesive soils there may
be no resistance losses at all during vibratory driving.
Unfortunately, there are only few dynamic test results available that can
quantify these soil resistance changes and for that reason, GRLWEAP does
not include a method that calculates the resistance losses automatically. In
fact, the few pile tests that were conducted first under a vibratory hammer
and immediately thereafter under an impact hammer did not indicate soil
resistance values of a significantly different magnitude under these two
hammer types.
Other effects also must be considered. For example, to a greater degree

than impact hammering will vibratory pile driving densify loose coarse
grained soils, yet reductions of soil density must be expected in very dense

soils. Calculation of the long term pile capacity based on pre-installation soil
parameters is therefore highly unreliable for vibratory driven piles. Even the
rate of penetration of the pile at the end of vibratory installation seems to
bear little relationship to pile capacity. For that reason, a final restrike test
with an impact hammer is often required when bearing piles are installed
with a vibratory hammer.
Interlock friction of sheet piles is an important resistance force which is

difficult or impossible to predict. It may depend on alignment of the two
adjoining sheet piles, the roughness of the lock, and whether or not the lock
is damaged or obstructed with sand.
The hammer model allows for the specification of a start-up time. It may be
assumed that during this time the hammer frequency increases linearly with
time from zero to the specified value. As a consequence, the vibratory
force increases quadratically (see Eq. 3.1) during that time. Note, however,
that the feared start-up, low frequency resonance in the soil (which may
cause damage to nearby structures) cannot be observed in the results of
the wave equation calculation since the soil is treated as for the standard
Smith analysis, i.e. without mass.
The hammer is normally suspended from a crane and it is sometimes

advantageous to maintain some Line Force, i.e. to keep some tension on
the hammer. On the other hand, a negative line force would be a so-called
crowd force and it could help push the hammer down which could be very
effective when the end bearing is high.
Note: Shaft resistance does not necessarily slow down penetration, but
may actually improve driveability by keeping a downward pressure
on the pile bottom during the upward motion of the vibration cycle.
The user should therefore not be surprised if penetration times
decrease for higher capacities under certain circumstances.
3.2.6.3 Preliminary Recommendations for Vibratory Hammer Analyses
PDI's experience of predicting bearing capacity or driveability from vibratory

hammer driving is limited. A good reference for the state of the art is
Holeyman et al., 2002. The following recommendations were developed
from theoretical considerations and a limited number of test cases.
a. Display forces or penetrations during the analysis and check for

consistency of traces; inconsistent (abrupt changes not repeated
from cycle to cycle) traces may indicate a numerical stability
problem. In that case analysis with a greater number of segments
is suggested.
b. Use the Smith-Viscous soil damping option. Since velocity and

displacement variations are sometimes very small, standard Smith
damping may be ineffective.

c. It appears that damping factors should be chosen higher than for
impact driving. It may be wise to double the damping factors
normally recommended for impact driving, because velocities
during vibratory driving are lower than for impact driven piles and
soil damping is known to be non-linear with relatively high forces
for low velocities.
d. For cohesive soils it appears reasonable to double the quakes that

are normally recommended for impact driven piles.
e. Soil setup factors may be quite different for impact and vibratory
driving. In cohesionless soils the shaft resistance may lose a
substantial amount of resistance and, for example, a setup factor
of 5 would be reasonable in a submerged sand (typically 1 or 1.2
for impact driving). On the other hand, for highly plastic cohesive
soils, not much resistance may be lost and the setup factor may be
as low as 1.0 for vibratory driving (often set to 2 for impact driving).
On the other hand soft clays or any material which tends to
behave in a thixotropic manner, may lose as much resistance as
for impact driving and should be considered with a higher setup
factor.
f. Do not specify waiting times to model the effect of driving

interruptions, since soil setup times and/or limit distance values
are even less known for vibratory driving than for impact driving.
g. Interlock friction should be modeled with additional shaft soil

damping or with an increased static end bearing. The latter model
seems more reasonable where sheet alignment problems exist.
Obviously, no quantitative recommendations can be given
because of the large variety of possible conditions.
3.3 Basic Hammer Models
An understanding of the dynamics of hammer, pile and soil is important for

performing a meaningful wave equation analysis and proper result
interpretation. It is therefore most important that the analyst understands
the working principals of pile driving hammers and their operation and
performance as described in the previous chapter and in the literature (e.g.,
Hannigan et al., 2006) and it is strongly recommended that the GRLWEAP
users familiarize themselves with that literature before attempting to
perform the dynamic analysis pile driving.
The following is a summary of important GRLWEAP hammer model details

for the three basic hammer types ECH, Diesel and Vibratory. Basic
schematics and associated model components of a typical single acting
ECH, an open ended diesel hammer and a vibratory hammer with bias
weight are, respectively, shown in Figures 3.3.1, 3.3.2 and 3.3.5.

3.3.1 External Combustion Hammers
3.3.1.1 The Ram of EC Hammers
The ram is the simplest and most important hammer component. For small
hammers a single mass element is often sufficient as its model. For
slender rams as encountered for example in modern hydraulic units, more
than one ram segment are necessary for a realistic simulation. Ram
segments should be less than 3 ft or 1 m long; if they are very short
numerical problems may be created because the critical time increment
would become very small.
With m being the number of ram segments, each segment, i, has a weight:
W ri = γi Ai ΔLi (3.3)
where γi, Ai and ΔLi are the specific weight, cross sectional area and length
of each ram segment I.
A ram spring is attached under each segment mass having stiffness:
kri = Ei Ai / ΔLi (3.4)
where Ei is the elastic modulus of the ram. Note that γi, Ai, and Ei may
need to be averaged over length ΔLi.
The bottom spring has an infinite slack, i.e. it is not possible to take any
tension. This bottom spring is combined with the hammer cushion spring
(note that a striker plate is not separately modeled; rather its mass has to
be considered in the helmet mass.
The combined model of the bottom (m-th) ram spring and the spring below
it must allow for separations and deformation caused by impact. For that
reason, a slack, dst (distance which spring extends at zero tension force), a
"round out" deformation, dsc, and a coefficient of restitution, c s, are used to
describe its behavior. A description of the characteristics of springs with
slacks is given in Section 3.6.
3.3.1.2 Assembly of EC Hammers
The assembly is only considered for EC hammers. As shown in Figure

3.3.1, their model usually consists of two assembly segment masses and
springs. The bottom spring has an unlimited slack, i.e. it cannot take any
tension. In most cases, their weights and stiffness values are calculated in
an approximate manner since there is no need for great accuracy. Only the
total assembly weight is important and since it is approximately equal to the
total hammer weight minus the ram weight, it is readily available. Unless
better information is provided by the manufacturer it is sufficiently accurate
to make two assembly weights of ½ (Hammer weight - Ram weight).

For hammers with columns linking base to top, the total assembly stiffness
may be approximated by the combined stiffness of the columns. See also
GRLWEAP Helps “External Combustion Hammer” and “Hydraulic Hammer
(Steel-to-Steel Impact) and Assembly Modeling”. If no accurate information
about the stiffness of the assembly is available, it is satisfactory to assign a
relatively soft spring which corresponds to a total compression deformation
of 0.005 mm (0.0002 inch) under the total weight of the assembly (kN or
kips) which is estimated to be total hammer weight W H (without helmet)
minus ram weight, W R. Since we are making two assembly springs, each
spring stiffness may be calculated from k1,a = k2,a = (W H – W R) * kWA
where kWA is either 400 (1/mm) or 10,000 (1/inch), yielding, respectively the
assembly stiffness values in kN/mm or kips/inch.

Figure 3.3.1: Schematic and Model of a Typical ECH hammer

3.3.2 Diesel Hammers
The diesel hammer’s ram is usually relatively slender and, therefore, is

modeled with several segments. Again, typical ram segments should have
a length less than 3 ft (1 m). The diesel ram is subject to pressures during
pre-compression, combustion and expansion which either slows it down
during descent or accelerates it upwards during its rebound. These
pressures are calculated as described in Section 3.3.3. Even though gas
pressures act between the ram and the impact block, the ram also impacts
against the impact block. The impact forces are transferred through the ram
bottom spring which is combined with the impact block spring. The impact
block mass contacts the hammer cushion spring. If no hammer cushion is
present then the impact block spring replaces then the ram bottom spring
and the impact block spring ram remain separate and act on top and bottom
of the impact block, respectively.
3.3.3 Thermodynamic Models of Diesel Hammers
3.3.3.1 Liquid Fuel Injection (Impact Atomization) Model
Liquid Fuel Injection is the most common design principle for diesel
hammers. The process is as follows (see Figures 3.3.3.1a and 3.3.3.1b):
 The ram descends and closes the exhaust ports.
 The pressure and temperature of the air trapped inside the

hammer cylinder between the ram and the impact block increase.
 Shortly after the ports are closed, fuel is injected into the chamber
under low pressure, i.e. in liquid form. The liquid fuel collects on
top of the impact block.
 The ram strikes the impact block, thereby causing the fuel to be
atomized. Pressure remains constant while the ram is in contact
with the impact block and before ignition starts.
 The atomized fuel starts to combust within a few milliseconds of

impact. The time lag between impact and combustion is the
combustion delay, td.
 The combustion process is finished within the combustion duration

tcd, i.e., within a few milliseconds of the start of combustion and
after the gases inside the chamber have reached their maximum
pressure.
 During combustion, the ram usually starts to separate from the

impact block. The corresponding increase in chamber volume
causes a reduction of the pressure inside the chamber.

 The ram reaches the ports, and chamber pressure drops to
atmospheric pressure.
Figure 3.3.2: Schematic and Model of a Typical Open Ended Diesel

Hammer

The foregoing stages of compression, combustion and expansion are all
considered in the GRLWEAP Liquid Fuel Injection (impact atomization)
model; the computational steps are shown below. Computed pressures are
expressed in terms of gage pressure.
Step A: At the beginning of compression, the chamber volume is equal to

Vi, the initial volume. It can be computed from the combustion
chamber volume, Vf, the cylinder area, Ac, and the compressive
stroke, hc:
Vi = Vf + Ac hc (3.5)
The position of the ram, ur, is:
ur = -hc (3.6)
With h being the hammer stroke, the ram velocity is:

1/2
vr = [(h -hc) 2g] (3.7)

The impact block position, uib, is zero at the time of port closure.
Step B: The ram has descended below the ports and the volume of the
chamber is:
Vc = Vf + Ac (uib - ur) (3.8)
The corresponding gage pressure, Pc, according to the Gas Law

is:
Pc = Pa ((Vi / Vc)cp - 1) (3.9)
Where Pa is the atmospheric pressure (14.7 psi or 101 kPa) and

cp is the exponent for adiabatic compression (1.4 for air, but 1.35
in GRLWEAP owing to some compression losses).
Step C: No particular computation is necessary to reflect the injection

process. However, throughout the compression cycle, a check is
made on the (negative) time until impact occurs (t=0):
ti = (uib - ur) / (vib - vr) (3.10)
where vr and vib are the ram and impact block velocity,
respectively. Actually, the time ti is not exactly equal to the time
until impact, primarily because vr changes under the effect of both
gravity and gas pressure. However, for cases of preignition,
where combustion starts before impact, this prediction is more
accurate than other available information. For preignition, the
combustion delay, td, is negative and combustion will start when ti
≤ td. Normally, the combustion delay is positive and between 0.5
and 2 ms.
Step D: Immediately preceding impact, the ram velocity is reduced by the

hammer efficiency leading to the reduced velocity vrr = vr (eh)½.
Step E: After combustion has started (the combustion delay has occurred),
two pressures are calculated. The first is the compression
pressure, Pc, as in Step B with volume Vi and Pa as the reference;
the second is the expansion pressure:
Pe = Pmax (Vc / Vi)ce - Pa (3.11)
with the maximum specified pressure, Pmax, and the initial

volume, Vi, as a reference. The exponent, ce, is the expansion
coefficient (ce = 1.25 for most L.I. hammers in GRLWEAP).
With tcd being the combustion duration and td < tc < td + tcd
where tc is the time of start of combustion, the final combustion
pressure is calculated from Pe and Pc by linear interpolation.
Normally, the combustion duration is between 0.5 and 2 ms.

Step F: Expansion takes place and pressure is computed according to
Equation 3.11.
Step G: The ports are reached, the gage pressure returns to zero. In
summary, for liquid fuel injection the following nine quantities are
used to compute the diesel hammer pressures.
Vf the combustion chamber volume

Ac the inside cylinder area
hc the compressive stroke
cp the Gas Law compression coefficient
ce the Gas Law expansion coefficient
Pmax the maximum combustion pressure
td the combustion delay
tcd the combustion duration
Pa the atmospheric pressure
The coefficients cp and ce are not easily calculated from measurement.

They may vary for a given hammer depending on its temperature, however,
based on observed strokes, reasonable average values have been
estimated. Thus, with atmospheric pressure known only six parameters
need be obtained from the hammer manufacturer. The first three geometric
values are usually well known. The timing quantities td and tcd vary only
slightly for normally performing hammers and are equal to 0.5 to 2 ms.
The most important parameter is the maximum pressure, P max. Ideally, this
value would be determined by measurement. However, as discussed, Pmax
varies depending on a variety of conditions such as ambient temperature,
altitude, fuel type, soil resistance, driving system properties, pile flexibility,
hammer state of maintenance, etc. In addition, high frequency pressure
waves in the chamber superimposed to the average pressure value make
interpretation of pressure measurements difficult. Furthermore, testing all
diesel hammers under controlled conditions would be prohibitively
complicated and expensive. Therefore, instead of measurements, the P max
values are iteratively computed such that the rated stroke is achieved by
the hammer model under test conditions. The computational procedure
followed for many of the hammers contained in the 2002 and later hammer
data file is described in Appendix B2.
3.3.3.2 The Atomized Fuel Injection Model
Atomized fuel injection is commonly used in diesel engines. The process

requires that the fuel is injected into the chamber beginning and ending at
certain piston positions or corresponding chamber pressures. The injection
pressure may be 1000 psi (7000 kPa) or higher. Such pressures produce a
finely distributed fuel spray. As soon as the fuel atomized in such a manner
is mixed with hot air, it combusts. The following phases are distinguished
(see Figure 3.3.3.2a and 3.3.3.2b).
 The ram descends and closes the exhaust ports.

 The air trapped inside the hammer cylinder between the ram and
the impact block is compressed and its temperature increases.
 When the ram is at a certain, small distance from the impact block,
atomized fuel is injected into the chamber. This ram position can
be computed from the "initial combustion volume", V ci. The fuel
starts to burn and reaches a maximum pressure level at the time
of impact (smallest volume or “chamber volume”).
 After impact, the ram rises and combustion ends, when the ram
has reached a certain distance from the impact block. Until the
corresponding final combustion volume, Vce, is reached the
pressure stays constant at Pmax.
 The ram rises further allowing the gases to expand and pressures
to decrease until it clears the exhaust ports and the pressure in the
chamber returns to the atmospheric level.

Differences between the atomized and liquid fuel injection models only
occur shortly before and after impact, i.e. Steps C and E. Most of the
compression and expansion periods are identically modeled for both types
of fuel systems. An exception is an expansioin coefficient which is typically
ce = 1.35 in the GRLWEAP models. For the atomized injection, the
GRLWEAP representation may be expressed as follows.
Step C: The gas pressure starts to increase from the precombustion

pressure, Pci, defined by the volume Vci (volume at which
combustion begins). It reaches the maximum combustion
pressure, Pmax, at impact (volume equal to Vf). In GRLWEAP this
phase was modeled by a quadratic interpolation between P ci, Vci
and Pmax, Vf.
Step E: The pressure stays constant at Pmax until the volume Vce has been
exceeded. At that point, both reference pressure and volume are
set to Pmax and Vce, respectively.
In summary, again nine quantities are needed to compute pressure for

atomized fuel injection. For atomized injection, the two volumes, Vci and Vce
take the place of the liquid injection parameters t cd and td. However, in
contrast to the rather insensitive liquid injection timing parameters, the two
combustion volumes have a very significant effect on the hammer
performance.
3.3.4 Closed End Hammers (Double Acting)
3.3.4.1 Double, Differential or Compound ECH
As the ram descends, a closed end hammer not only falls under gravity but
also experiences a downward pressure. For a double, differential or
compound acting ECH, GRLWEAP does not differentiate as to how the ram
has obtained its impact velocity and it is not necessary to deal with the
active downward pressure. Instead of working with the actual stroke, it is
therefore necessary to calculate an equivalent stroke:
he = Er/W r (3.12)
where Er is the hammer's rated energy and W r is the weight of the ram.
With eh being the hammer efficiency, the impact velocity is then:

½
Vri = (2g he eh) (3.13)
If a double acting ECH is run at a pressure less than rated, then the energy
provided by the pressure is proportionally lower. Given the portion of the
energy that is provided by the pressure, f ep, and the ratio of actual to rated
pressure, rap, the reduced equivalent stroke becomes:
her = he [1 - fep(1 - rap)] (3.13a)

For example, if the pressure provided energy component were 40% of the
rated energy, then ram weight times fall height would be 60% of the rated
energy. If the hammer were run at 70% pressure (r ap = 0.7), then the
equivalent stroke would be:
her = he[1 - 0.4(1 - 0.7)] = 0.88 he (3.13b)
For inclined pile driving the same stroke reduction consideration has to be
made as for single acting hammers.
3.3.4.2 Closed End Diesel Hammers
For double acting diesels, the force on the ram top is computed to
determine (a) the hammer blow rate, (b) the hammer-pile-soil behavior
during the precompression phase, and (c) the necessary fuel reduction to
avoid uplift.
GRLWEAP calculates gage pressure on the ram top based on an

expansion coefficient, cbp, (which is usually 1.4). Thus, the bounce
chamber pressure, Pb, may be calculated from:
Pb = Pa (Vbi/Vb)cbp - Pa (3.14a)
where Vbi is the initial volume in the bounce chamber:
Vbi = hb Art + Vct (3.14b)
with hb being the "compressive stroke" of the bounce chamber, i.e., the
distance from the bounce chamber ports to the top of the cylinder. A rt is the
cross sectional area of the ram top and Vct is the compression tank volume.
The maximum stroke at which uplift is imminent is determined from the

reaction (cylinder) weight of the hammer, W c, yielding the uplift pressure:
Pu = W c/Art (3.15)
and by substituting Pu into Eq. (3.14a) for Pb, the volume and therefore
position of the ram at uplift is easily calculated from Eq. (3.15).
Note that the closed end diesel hammer has a reduced effective stroke
when used on an inclined pile. The user therefore should not only reduce
the reaction weight (Options/Hammer parameters), the hammer
gravitational acceleration, the hammer efficiency (see Help Table), but also
the pressure such that the maximum calculated stroke does not exceed the
maximum geometric stroke times the cosine of the inclination angle.

3.3.5 Vibratory Hammer Model
The GRLWEAP hammer model consists of 2 masses which are connected

by a linear spring and by a linear dashpot (Figure 3.3.5) has to be redone.
There may be hammers with more than two or only one mass, however, the
GRLWEAP model currently does not represent these relatively rare cases.
The bias (upper) mass serves as a vibration isolator and adds downward
force to the driving system. It is also subjected to an upward directed force,
called the crane line force, FL, which may represent the crane line pull
(usually it may be assumed that the hammer's weight is fully supported by
the pile and then FL = 0). Downward directed (a negative value), it would
represent a crowd force, which would help the pile to penetrate more
quickly. Upwards directed (positive), it could cause an extraction, if it is
greater than the weight of the hammer plus the weight of the pile. Note,
however, that the program will not calculate an upward extraction rate of
movement.
GRLWEAP applies the sinusoidally varying vibratory force, F V, to the

hammer's oscillator (lower) mass (which contains the eccentric masses).
The power provided through this force is monitored and held to at most the
rated power value. The vibratory force may also be modified (reduced) by
an efficiency value which, in general, is left at unity (no efficiency reduction).
The vibratory force is not affected by pile batter. Thus, ignoring the inertia of
the eccentric mass (which is generally not accurately known) due to the
motion of the bottom (oscillator) mass:
2
FV = me [ω re (sin(ωt)] (3.16)
with
me = the sum of all eccentric masses,
re = the radius of the center of gravity of the eccentric masses
from their center of rotation
The hammer model also considers a spring constant for the connecting
spring between upper and lower mass. A dashpot constant can be specified
for a dashpot in parallel with the connecting spring impact (as for the
hammer cushion discussed in Section 3.4, Eq. 3.17). A clamp (sometimes
also called jaws) weight, specified in the data input, is added to the weight
of the oscillator.
During the start-up time period the frequency of the hammer is linearly
increased with time in GRLWEAP. As a result the vibratory force increases
during that time period quadratically. In general, the start up time period
analysis has little effect on the final results. It may be used for special
studies. It cannot, however, be expected that the realistic resonance effects
can be detected with a variable frequency analysis, because of the
simplified soil resistance analysis according to Smith.
The upper mass of a vibratory hammer is subjected to the upward directed

crane line force. It can be input negatively to simulate a crowd force.

Figure 3.3.5: Schematic and Model of a Vibratory Hammer
The user can modify the frequency for vibratory hammers in the same way
in which the stroke can be modified for impact hammers. Note, that
although the highest (rated) frequency provides for the highest forces, the
pile may actually penetrate easier at lower frequencies and it is, therefore,
recommended to check the penetration times for a variety of frequencies.
However, it may not be wise to reduce the frequency to values less than 10
Hz where it is known to cause undesirable resonance. Also, for very low
frequencies it may be necessary to increase the analysis time (in General
Options/Numerical) so that sufficiently many vibration cycles are analyzed.
A check of the graphical variable vs time output may be helpful in assuring
proper convergence.
3.3.6 Hydroblok Hammers
Since 2002, GRLWEAP does not include a working model of the Hydroblok.
For further information, please contact PDI.

3.3.7 Drop Hammers
Drop hammers are not very easily standardized because of their many
possible configurations. There are two main categories, (a) the drop
hammer which is freely released and (b) the drop hammer which has to
unspool a winch. Obviously in the latter case higher energy losses must be
expected not only because of the inertia of the winch but also because the
operator then tends to catch the ram just before impact so as to maintain
stability. In both cases the hammer stroke is probably not very well known.
These uncertainties have to be covered by the hammer efficiency. The
remaining model is simply that of an external combustion hammer.
3.3.8 Hammer Energy Losses
The wave equation analysis of an impact hammer requires the calculation

of ram impact velocity, vri. During the fall of an ECH ram, the pile does not
experience dynamic forces. However, the weights of assembly and helmet
create a static force in pile and soil. Thus, the dynamic analysis only has to
cover the time period during and after impact.
For the diesel hammer, appreciable forces are exerted onto the pile before
impact due to air compression in the cylinder. In general, the pile already
has a noticeable velocity prior to ram impact and soil resistance is
activated. Therefore it is necessary to start the analysis of diesel hammers
at the time of port closure.
It has been stated earlier that energy losses in the hammer are easily
considered using the hammer efficiency, e h, and certain rules of assigning
efficiency values have been set up. For hammers with impact velocity
monitoring, reasonable results are achieved with an efficiency eh = 0.95 if
the monitored energy is the basis for the analysis. Obviously, most losses,
such as friction, have been considered for these hammers by the impact
velocity measurement. Only losses occurring during the impact event itself
(e.g. due to hammer-pile misalignment) have to be considered. For
vibratory hammers, the efficiency concept is not strictly applicable.
However, in order to allow for some reduction of the output force, relative to
the theoretical value, an efficiency multiplier (less than or equal to 1.0) may
be applied to the calculated centrifugal force.
The following efficiency values have been included in the hammer models
in the GRLWEAP hammer data file. It is recommended that the analyzing
engineer carefully review and modify these efficiency values, if
measurements so indicate. Furthermore, because of the uncertainty of
actual hammer behavior it is recommended to analyze (a) conservatively for
stresses at a somewhat higher efficiency than normal or (b) conservatively
for bearing capacities and/or blow counts with a slighlty lower efficiency). A
± 0.1 variation would be reasonable (even for a 0.95 efficiency, since values
above 1.0 have occasionally been observed, maybe due to overstroking.
The following recommendations for drop hammer efficiencies are just that

and like all efficiency values should be backed up by individual
measurements.
eh = 0.67 for single acting air/steam hammers and for drop hammers
with free release
eh = 0.50 for double acting air/steam/hydraulic hammers and drop

hammers with spooling winch
eh = 0.80 for all types of diesel hammers
eh = 0.80 for hydraulic hammers, single acting or power assisted but

not double acting and without impact velocity measurement
eh = 0.95 for hammers whose rating is based on measured impact

velocity
eh = 1.0 for vibratory hammers
Again, these recommendations represent an average hammer behavior and

efficiency values may be required to match measurements. Note also that
eh normally covers losses occurring both during ram descent and impact.
The efficiencies in the GRLWEAP hammer data file have been chosen with
no consideration of hammer manufacturer. Hammer performance
differences should be individually accounted for by the user. For hydraulic
hammers, a more uniform rating has been adopted by combining the free-
fall hydraulic hammer category of pre-2002 versions with the category of
other modern hydraulic hammers without impact velocity measurements.
Hammers which optionally can be equipped with impact velocity monitoring
sensors, have been given a 0.8 efficiency as though they are not equipped
with that feature. In that case, the user is responsible for modifying the
efficiency. In fact, under all circumstances, it is the user’s responsibility to
check all hammer data of the GRLWEAP hammer data file prior to using it.
3.3.9 Inclined Pile Driving
Since 2010 GRLWEAP does provide for an input of the pile inclination
(Options/ Pile Parameters/ Batter-Inclination), and gives the analyst
immediate recommendations which are also given in the On-line Help.
However, in any case, depending on the hammer type, the user has to be
aware of and consider one or more of the following energy losses and
model adjustments:
Hammer Friction: a reduction of the hammer efficiency should be

considered according to the help table for all except vibratory hammers.
Reduced Stroke: all hammers whose effective, vertical stroke is limited by

the hammer inclination should be analyzed either with a reduced stroke or
an efficiency reduction. Exceptions are open ended diesel hammers,

hammers whose rating is based on impact velocity monitoring and vibratory
hammers. Note: reducing the gravitational acceleration of the hammer does
not affect the ram’s mass or impact velocity, however, it does reduce the
static assembly and helmet weight resting on pile and soil prior to impact.
Reduced Reaction Weight: as stated earlier the reaction weight of closed

ended diesel hammers must also be reduced to model the reduced
maximum bounce chamber pressure. The input of a reduced hammer
gravitational acceleration does not affect the reaction weight.
3.3.10 Driving at the Pile Bottom or at an Intermediate Pile Location
This is an Offshore Wave option.
It may be desired to locate a hammer not at the pile top but at an

intermediate location along the or at the bottom (Figure 3.3.10.1). Actually,
bottom pile driving is not an unusual technology, in fact, it is frequently done
even on land.
Figure 3.3.10.1: Schematic of bottom and intermediate pile driving

Only EC hammers can be used in this analysis. It is assumed that the ram
of the hammer strikes a hammer cushion and that the hammer cushion is
supported by a plate (the helmet in the input). This plate must be somehow
supported by the pile. It is assumed that this pile support combined with the
helmet have a certain stiffness which is an additional input (Figure
3.3.10.2). A further additional input is the hammer location which can have
length values between 0 and the pile length. If it is zero then the hammer
drives at the pile top. If it is equal to the pile length, then it drives at the
bottom. It is interesting to view the stresses along the pile (extrema tables)
when the pile is driven at an intermediate location.
Figure 3.3.10.2: Schematic of bottom and intermediate pile driving
3.3.11 Static Soil Column Weight
This is an Offshore Wave option
This option may be useful when analyzing an intermediate hammer position

or a bottom plate inside the pile some distance above the pile toe. However,
even a normal open ended pipe pile which drives in the coring (non-
plugging) mode has a soil column acting as a static weight on the soil.
While it may be assumed that this soil mass has negligible stiffness
compared to the pile it potentially adds a large additional weight on the soil
at the bottom of the pile. This GRLWEAP feature allows for consideration of
the internal soil weight to be considered in the static equilibrium analysis
which occurs prior to the dynamic analysis. Note: the static soil resistance
in a driveability analysis should be equal to the weights of soil column and
pile plus the load that can be supported by the pile. This option may be

helpful when comparing driveability of a coring pile with one driven at its
bottom (empty pile).
If it is desired to consider the mass effect of this plug in the dynamic

analysis, then that must be accomplished by an increased specific weight in
the pile model (P1 input form); this would assume that the stiffness of the
soil mass can be ignored.
The input of the static soil column weight requires the following input
(Figure 3.3.11.1).
 Effective Soil Column Area, AS;

 Buoyant Soil Specific Weight, γS;
 Maximum Soil Column Length, LS.
Figure 3.3.11.1: Soil column weight model
In the calculation, the total plug soil weight is evenly distributed among the
pile segments which are located between segments No. i and N when
performing the static equilibrium analysis prior to the dynamic analysis.
In this notation, i is the segment where the soil column begins and N is the
bottom segment number. The soil column, LC, is assumed to begin at either
LS or Lp (pile penetration), whichever is smaller. The total plug weight is
WP = AS γS LC .
3.4 Driving System Model
The driving system consists of a striker plate, hammer cushion, helmet,

helmet insert and, for concrete piles, a pile cushion. This system is
represented by two nonlinear springs and a mass. For the ECH the spring
for the hammer cushion is modeled in series with the ram spring (Figure
3.4). For all impact hammers, the pile cushion spring is modeled in series
with the pile top spring.
For diesel hammers, if no hammer cushion is present, then GRLWEAP

splits the impact block spring and places one spring on top of the impact
block and the second one on top of the helmet. For ECH without hammer
cushion, the bottom ram spring acts on top of the helmet.

Figure 3.4: Schematic and Model of the Driving System
For systems without helmet mass, the ram’s bottom spring acts directly on
the pile top spring for ECH. For diesel hammers, the pile top spring is
combined in series with the hammer cushion spring (if any) and/or the
impact block spring. Note that earlier versions of GRLWEAP required a
helmet mass for diesel hammers. Since 2002 this requirement has been
removed, because diesel hammers have now been introduced (e.g., “Direct
Drive” hammers) whose impact block strikes the pile directly.
The mass between hammer and pile is called “Helmet” in GRLWEAP

terminology, although it is also often called the “Cap”. In any event, the
weight of devices like the striker plate, hammer and pile cushion, pile
adapters or inserts, etc. should all be included in the "helmet mass", since it
is really the total mass separating hammer components from pile top.
The driving system model also contains a dashpot in parallel with the
hammer cushion spring. Its damping constant is computed from:
½
cdh = 1/50 cdhi (krma) (3.17)
where cdhi is a non-dimensionalized input value, kr is the hammer cushion

stiffness, and ma is either the impact block (diesel) or helmet (ECH) mass.
The default value of cdhi is 1. The user can remove this dahpot whose
function is to suppress spurious vibrations by entering certain multipliers
(see General Options/Damping and On-Line Help: Damping Options
/Hammer).

3.5 Pile Model
The pile model consists of springs, masses, and dashpots (see Figure 3.5).
The pile is divided into N segments whose lengths are given by:
Li = αiL (3.18)
The program chooses the number N such that approximately 1 m long pile
segments result. (It is sometimes reasonable to a user larger N number for
increased accuracy of calculation. For example, for uncushioned hammers,
an N producing 0.1 m segment lengths has already been successfully tried
where measured records had to be matched.)
In Eq. 3.18 L is the total pile length and αi is a multiplier which is normalized
such that:
∑ (αi) = 1.0, i = 1,2,...,N (3.19)
Ordinarily, the αi values are all assumed to be equal to 1/N by the program,
however, the user may modify these values (Options/ Pile Segment Input).
Weights of pile masses and their stiffness values are calculated as for rams
(Eq. 3.3 and 3.4).
In pre-2002 versions of GRLWEAP, the pile's static weight was not

considered in the Bearing Graph analysis. Thus, it was tacitly assumed that
the soil supports the pile weight before the ram impacted. The GRLWEAP
capacity calculated from the bearing graph and observed blow count would
then be the limit load which can be placed on the pile top. This also implied
that the ultimate pile capacity would really be the GRLWEAP capacity plus
the pile weight. The pile weight, however, was considered in residual stress
analysis, in the vibratory analysis, and by subtraction of a “dead load”, in
the driveability analysis option. This created a confusing situation when
Bearing Graphs were compared with driveability results. GRLWEAP now
allows the user to enter two gravity values, one for the pile, g p, and one for
the hammer, gh. Since the basic input for the mass of pile, helmet and
hammer is done in the form of their weight, the program first converts these
2 2
values to mass by division with g = 9.81 m/s (32.17 ft/s ). The effective
static weights, however, are then backcalculated by multiplication with gp
and gh. Normally, gp = gh = g, however, the user may modify g p and gh to
account, for example, for buoyancy or pile batter.
The gravity values are used in an equilibrium analysis, which precedes the
dynamic analysis to calculate initial soil and pile deformations and forces.
For the hammer, the ram is not included in this analysis since it is expected
that the ram is not supported by the pile prior to impact. Note that a
reduction of pile and/or hammer gravity should be considered for battered
and underwater pile driving.

A third parameter, the pile damping value, can be specified by the user.
Since little is known about the correct structural damping model, and since
this type of damping produces relatively small energy losses compared to
soil damping, an elaborate model does not seem justified.
Thus, viscous damping was assumed as follows:
cdp = (1/50) cdpi (EA/c) (3.20)
with cdpi being a non-dimensionalized input number and EA/c being the
impedance of the pile top; cdp is the same for all pile segments regardless of
segment length or impedance. For piles with greatly varying cross sectional
or material properties, it is suggested that comparison runs be made with
different cdpi values to test the sensitivity of the solution to pile damping.
(The input can be made in General Options / Damping).
Figure 3.5: Wave Equation Models for Various Hammer TypesThe pile
data input also contains additional parameters which are not used for the
generation of the pile model. These values include:
 Perimeter, which is needed in driveability analyses and static

geotechnical analyses (ST, SA, CPT, API) for the calculation of
shaft resistance forces from unit resistance values. (Note: it is
sometimes convenient to consider inside friction in an open ended
pipe by an increased perimeter).
 Toe Area, which is needed in driveability analyses and static
geotechnical analyses (ST, SA, CPT and API) for the calculation
of end bearing. (Note: in the S1 table the Toe Area can be varied

such that, for example, the plugging can be considered in certain
soil layers and not in others by entering, respectively, the full pipe
area and the toe steel cross sectional area.
 Pile size and Pile type, both of which are used for the assignment
of pile toe quakes and for finding in the data base the appropriate
manufacturer’s recommended driving system (which is a function
of hammer model, pile type and pile size).
 For non-uniform piles only, a Critical Section Index which allows

for selection of that portion of the pile model that is considered
important for the output of “maximum” stresses. This index is
either 1 or 0. The user should set it to 1 for those sections of the
non-uniform pile model whose maximum stresses should be
considered for final output. The CSI is only reasonable when two
or more pile materials are analyzed. For example, a system
consisting of a steel follower driving a concrete pile will have
numerically highest compression stresses in the steel, however,
the concrete stresses will most likely be of more interest and the
CSI should, therefore, be zero for all steel sections while the CSI
of the concrete portions of the pile profile should be set to 1.
3.6 Splice/Slack Model
GRLWEAP uses a splice/slack model which has also been incorporated

into the models for the cushions, impact block/helmet, and pile top. This
model contains three parameters: a tension slack, dst, a coefficient of
restitution, ca, and a round-out deformation or compressive slack, dsc. The
general shape of the resulting force-deformation curve is shown in Figure
3.6.

During compression of the splice model, force increases quadratically
(stiffness increases linearly) with respect to deformation until the round-out
deformation, dsc, is reached. The corresponding force at this point is F lim.
Beyond this point, force increases linearly, with the slope given by the
spring stiffness, k. During the subsequent expansion, force decreases
2
linearly with respect to deformation, but this time the slope is k/ca . Note,
however, that the deformation, over which round out occurs, is smaller
during unloading than during loading for c a values less than 1.
For the extension of the spring, GRLWEAP applies the same rounding
procedure. However, the spring stiffness begins to increase from zero only
after the spring has extended beyond the slack distance, d sl. Within this
separation distance, the spring force is always zero.
For springs, which should not take any tension at all, the user should set d sl
to an arbitrarily large value such as 9 ft or 99 mm. For all other interface
springs, experience shows that a 0.01 ft or 3 mm (default) value is
adequate. Attempts to match measurement results have shown that only
very soft materials, such as a plywood cushion, require a larger than the
default round-out value. In this way, cushion, pile top, and splice forces can
be calculated with the same algorithm. Because of the rounding feature,
numerical stability of the analysis of splice piling is assured. Note that this
rounded-out splice model is always used in GRLWEAP, when d sl > 0.
The splice model is only needed for those splices which allow for some
forceless deformation (slack). For example, mechanical splices of concrete
piles fall in this category while welded splices of steel piles do not. Also a
can splice (has no tension connection at all) could be modeled with the
splice model. As an example, the can splice, which usually includes a thin
plywood sheet, could be modeled with
 dsc = 3 mm (0.01 ft), default
 dsl = 99 mm (9 ft), an arbitrarily large number for an
unlimited extension, and
 ca = 0.5 (for wood)
3.7 Soil Model
3.7.1 The Basic Smith Static Resistance Model
GRLWEAP’s soil model is basically a Smith approach, i.e. it consists of a

spring and dashpot (Figure 3.5). The elastic spring yields at a pile segment
displacement equal to qi (quake). Beyond that point, there is no further
increase in static resistance, Rsi, with increased displacement, ui. Thus, as
long as the pile segment’s velocity is positive (downward), i.e., during the
initial loading phase,
Rsi = (ui/qi) Rui for ui < qi (3.21a)
and

Rsi = Rui for ui > qi (3.21b)
where Rui is the ultimate static resistance at segment i. During unloading,

i.e. when the pile segment has an upward (negative) velocity, the spring
rate is equal to that used in the loading path.The most negative shaft
resistance value is –Rui. The lowest toe resistance value is equal to zero.
For shaft resistance elements, the soil resistance can be come negative;
however, it cannot be less than -Rui. At the toe, the static soil resistance
cannot be less than zero.
The static shaft resistance and end bearing values, Rui, added together
make up the ultimate capacity of the pile, R ult. For the bearing graph
analysis it is customary to choose 10 different Rult values, one of them
usually equal to the expected or required R ult. Thus, in a bearing graph
analysis, the static geotechnical analysis only serves to determine how
many percent of Rult are expected to act along the shaft and how the shaft
resistance is distributed along the pile. Also, the end bearing percentage is
found in that manner since it is the difference between shaft resistance and
total resistance. Of course, it is wise to make a reasonably accurate static
geotechnical analysis prior to the dynamic analysis, not only to find a
meaningful resistance distribution, but also to determine the most likely
penetration where the required capacity will be obtained. Please note that
these static formula methods (such as ST, SA, CPT and API) generally
calculate a long term resistance while at the end of driving both a different
resistance distribution and total capacity must be expected due to the
dynamic effects on the resistance (the reverse effects of setup and
relaxation). This long term capacity would correspond to a restrike situation.
To be strictly correct, therefore, a so-called SRD (Static Resistance to
Driving) analysis would have to be performed as it is usually done for a
Driveability analysis.
While the Rui values are practically assumed to construct a bearing graph
(which then serves to find a capacity given an observed blow count), the
driveability requires that an accurate static analysis is performed for each
depth where an analysis is to be performed. This process is discussed in
detail in Section 3.12.2.
Shaft quakes have been found to vary little and clear relationships between
soil type and shaft quake or pile size and shaft quake have not been
established. A 2.5 mm (0.1 inch) shaft quake is reasonable and generally
accepted. Toe quakes, on the other hand, can vary widely. In general,
hard soils or rock are stiffer and the toe quake (the inverse of the toe
resistance stiffness) is therefore smaller than in softer soils. Furthermore,
displacement piles such as a concrete or closed ended pipe piles require
much larger displacements to activate the ultimate toe resistance than non-
displacements piles. The reason is that activating the ultimate capacity then
requires a much larger pile toe penetration, often leading to pile size
dependent failure criteria (e.g., D/30 or D/10). The GRLWEAP toe quake
recommendation similarly expresses its magnitude in terms of a function of
pile diameter (size), D. For very dense or hard soils the recommendation is

D/120; for softer materials it is D/60. Please note, that much larger toe
quake values have also been observed and that toe quakes are often quite
different when driving, restriking or statically loading the same pile. Large
toe quakes can cause tension stresses even when resistance values are
high. Large toe quakes also produce high blow counts and can, therefore,
make driving of displacement piles very difficult.
For bearing graphs, a more detailed though rarely used input mode is also
available allowing for specification of different shaft quakes for each pile
segment. See Options/ Soil Parameters/ Soil Segment Damping/ Quake/
Individual Damping Input for Each Segment. Activating the shaft quake
input in this window, however, requires that first the static resistance
distribution is entered individually for each segment, after choosing
“Detailed Resistance Distribution” in the resistance distribution drop down
menu.
For residual stress analyses or vibratory analyses, both of which calculate

pile motions and forces under consecutive loadings, the possibility exists
that the pile toe is pushed upwards a certain distance above the maximum
penetration achieved under the previous blow or compressive cycle.
GRLWEAP static toe resistance model has therefore been modified for
these two types of analyses such that the static toe resistance will remain
zero until the pile toe has moved through the cavity developed under the
previous impact or compressive cycle.
3.7.2 Soil Damping
3.7.2.1 The Basic Smith Damping Model

GRLWEAP’s standard damping model is identical to original Smith model.
Other models can be chosen in Options/ General Options/ Damping.
Rdi = jsi |Rsi|vi (3.22)
where Rdi is the damping resistance force and j si, vi and Rsi are the Smith
damping factor, the pile segment velocity, and the static resistance force, all
at segment i, respectively. Smith's damping factor has units of time over
length. Even though more than half a century has passed since Smith
developed this model, today we are still recommending the same basic
factors for damping along the shaft, i.e., 0.15 s/m (0.05 s/ft) for sands and
0.65 s/m (0.2 s/ft) for clays. Different values are used where measurements
have been made or in mixed soils. Only for toe damping recommendation
changed to 0.5 s/m (0.15 s/ft) for all soil types (see also 3.7.2.3).
The second choice is called Smith viscous damping and it replaces the term
|Rsi| in Eq. 3.22 by Rui, i.e the ultimate capacity value which, like j si, is a
constant. Thus Eq. 3.23 expresses a linear viscous damping model.
Rdi = jsi |Rui|vi (3.23)

This approach is recommended for RSA, because, in agreement with
measurements, the Smith-viscous model produces dampened pile motions
after pile rebound when Rsi values are small. Also for vibratory hammers,
the Smith viscous approach appears to be preferable because of the
relatively small velocities of vibratory driven piles. (Please note, however,
that viscous damping for vibratory hammers works in both directions,
upwards and downwards; the damping effect is, therefore, not necessarily
one that reduces driveability. Also for lack of correlation data, there is no
proof that the GRLWEAP model is reasonably accurate for vibratory
analyses).
3.7.2.2 Extensions to the Damping Model
Note: The following three extensions of the damping model are usually
reserved for research and require matching with measurements for
successful implementation; they can be chosen in Options/ General
Options/ Damping.
The third damping choice is a non-dimensionalized viscous damping.

½
Rdi = jci vi (kpimpi) (3.24)
Here jci is the Case (Institute of Technology) damping factor. Note that the
bracketed expression on the right hand side of Eq. 3.24, i.e. the square root
of the product of segment stiffness and mass, is equivalent to the
impedance of the pile segment (Young's Modulus, E, times the cross
sectional area, A, divided by wave speed, c). This approach produces the
½
same linear damping as the Smith-viscous one if jci = jsi Rui / (kpimpi) .
A fourth expression allows for damping calculations according to Coyle, et

al., (1970), i.e. with an exponential approach:
n
Rdi = Rsi jgi vi (3.25)
where jgi is the Gibson damping factor with units of time over length to the
1/n power where n is an exponent, typically 0.2. Because of numerical
problems with this approach, another damping equation was proposed by
Rausche, et al., (1994):
n
Rdi = Rai jRi vi (vi/ vxi) (3.26)
where jRi is the Rausche damping (also with units of time over length to the
1/n power), vxi is the maximum pile velocity and Rai is the maximum
activated static resistance value of segment i. Both vxi and Rai are values
that have occurred prior to or at the time of calculation of damping. After v xi
and Rai have reached their maxima, Rdi is essentially linearly viscous.

3.7.2.3 Distribution of Shaft Damping
Smith’s approach varies damping forces along the shaft in two ways: it
allows for different damping factors for different soil layers with cohesive
materials getting a higher and granular soils a lower damping factor.
Secondly, by making the damping force also a function of static resistance,
a higher static resistance will also produce higher damping given the same
damping factor and velocity.
In standard bearing graph analyses which are normally done with either
Smith or Smith-Viscous damping factors, we are usually a bit careless
merely choosing a constant damping factor for the shaft. This shaft
damping factor should be a weighted average over the shaft of the pile,
weighted with respect to static soil resistance magnitudes. The static
geotechnical analysis options (SA, ST, CPT and API) automatically perform
this averaging.
For bearing graphs, a more detailed though rarely used input mode is also
available allowing for specification of different damping factors for each pile
segment. See Options/ Soil Parameters/ Soil Segment Damping/ Quake/
Individual Damping Input for Each Segment.
In non-research applications, either Smith or Smith-Viscous damping

should be used. For these two damping approaches, damping factors are
practically identical, with the Smith-Viscous approach yielding somewhat
higher blow count results.
In a driveability analysis, the damping factors are chosen for each layer
according to their soil type. The static geotechnical analysis options (SA,
ST, CPT and API) help select these values and automatically enter them in
the resistance distribution table (S1).
For Case Damping the standard input also consists of one shaft and one
toe damping factor. After multiplication with the impedance (conversion of a
non-dimensional to a viscous damping factor), the total skin damping factor
is distributed among the pile segments in proportion to the static resistance.
Again, the three non-Smith type damping models (Case, Coyle-Gibson,

Rausche) are not recommended for non-research applications.
3.7.2.4 Selection of Damping Factors
Damping factors would be quite different for any other type of damping
approach; in other words, changing the damping definition must be
accompanied by appropriate changes in damping factors. Generally,
applicable damping factor recommendations are only available for Smith
damping.
Normally, for Bearing Graph analyses, GRLWEAP users input a constant

damping factor even where the soil is layered. For conservatism of capacity

results, such average values may be somewhat biased towards the higher
clay values. When choosing an average shaft damping value for a multi-
layer soil, the user should remember that damping according to Smith is
greater in the layers with higher static resistance. Accordingly, the average
damping factor should be a weighted average with respect to the static
resistance components (see also 3.7.2.3).
For mixed soils or silts an average value also has to be chosen. For
example, the shaft damping factor for a soil consisting of clayey silt, a value
of 0.5 s/m (0.15 s/ft) may be chosen which is somewhere between sand
(normally js = 0.15 s/m) and clay (normally js 0.65 s/m). For a non-cohesive
silt, the damping factor chosen may be closer to sand, e.g. 0.33 s/m (0.1
s/ft).
Toe damping input is generally rather simple, requiring only one factor for
all soil and pile types. Note, however, that the 0.5 s/m (0.15 s/ft)
recommendation is an average over potentially widely varying values. One
exception should be made for this simple approach and that is when driving
a pile to hard rock is considered. In that case the standard toe damping
option may be too high and a lower factor such as 0.15 s/m (0.05 s/ft) may
be more appropriate. Shales, soft or moderately hard limestones,
weathered rock among other intermediate geotechnical materials probably
behave dynamically more like their underlying soil components and their
damping factors should reflect that (also as far as shaft damping is
concerned).
3.7.3 Soil Model Extensions
So-called research extensions of the soil model, described in Rausche et al.

(1994), include the Plug, Toe Gap, Hyperbolic Toe Quake factor and
Radiation Damping Models for Toe and Shaft. These extensions should
only be used for research, e.g. for correlation purposes with measured
data.
The Plug would be entered either with a plug toe area, which the program
uses to calculate a plug mass, or directly as a plug mass. This plug only
exerts compressive inertia resistance forces onto the pile bottom for a brief
time period.
A Toe Gap is a short distance between pile bottom and a hard soil layer, as
it may occur when a pile with little skin friction separates from rock during
rebound. This feature makes blow count calculations uncertain, but is
sometimes essential to explain large quakes and is generally only important
in signal matching (CAPWAP) and not in wave equation analyses.
The Hyperbolic Toe Quake Factor allows for a rounded-out toe resistance
vs. toe displacement behavior. This factor multiplied with the toe quake
(which defines the slope of the hyperbole at the origin) indicates at which
pile toe displacement the ultimate resistance value is reached. Again, blow
count calculations are more erratic when using this model.

The Radiation Damping Models include a mass and a dashpot underneath
the mass which represent the soil surrounding the pile soil interface
represented by the Smith soil model. Recommendations for these model
parameters are not available.
3.8 Numerical Procedure and Integration
3.8.1 Time Increment
Smith’s lumped mass model is mathematically stable only if the

computational time increment is chosen shorter than the shortest (critical)
wave travel time of any segment I. The critical time increment is the time
that it takes the stress wave to travel through the pile segment:
tcri = Li/ci (3.27)
or for a lumped mass element:
tcri = (mi/ki)
½
(3.28)
where mi, ki, Li and ci are the segment mass, stiffness, length, and wave
speed in segment I, respectively. The wave speed of the segment is:
1/2
ci = (Ei /ρi) (3.29)
with ρi being unit mass of the segment. Where pile properties change
within a segment length, all segment properties are averaged.
In order to avoid instability, the computational time increment, t, is chosen

as:
t = min(tcri)/ (3.30)
where min(tcri) stands for the minimum critical time increment of all
hammer and pile segments, and  is a number greater than 1. The program
defaults to  = 1.6 (since input is in percent it would be input as 160).
However, if numerical instability is indicated in the Numerical Output the
user has the responsibility to choose a larger value (e.g. 300) in Options/
General Options/ Numeric/ Time Increment Ratio.
While the critical time of the hammer-driving system-pile model is normally

determined from the stiffest segment in hammer or driving system, the
program also checks the pile segments, considering the effects of soil
resistance on the stiffness of the pile segments. As a consequence,
GRLWEAP may select the computational time increment with smaller
values for high capacities than for low capacities.

3.8.2 Analysis Steps
3.8.2.1 Prediction of Pile Variable at Time j
The computation starts with a pre-integration (see block diagram in Figure

3.8.2.1a). Velocity values, vij, at segment, i, and time step, j, are calculated
in a simple Euler integration from accelerations, aij. Displacements, uij, are
predicted from vij-1 and uij-1, i.e. from their value at the previous time
increment. For example, the ram of an ECH may be a simple mass, m r,
that has an initial velocity equal to the ram impact velocity, v ri. Furthermore,
at the beginning of the computations (j = 1) the first ram segment (i = 1)
acceleration becomes
a11 = gH (3.31)
with gH being the gravitational acceleration of the hammer.
In this case the pre-integration produces:
v12 = vri + a11 t (3.32a)
and
u12 = u11 + vri t (3.32b)
This process is repeated for all hammer, driving system and pile segments.

Figure 3.8.2.1a: Block Diagram of Predictor-Corrector Analysis

3.8.2.2 Forces at a Given Segment
The force of the top spring on a segment is calculated from spring stiffness
and spring compression, i.e. the difference between the displacements of
neighboring segments (see Figure 3.8.2.1b).
t
Fsij = ki (ui-1 - ui) (3.33)
The stiffness ki is that of any hammer, driving system, or pile segment,

subject to modification if there is a positive slack dst at spring i.
The force of the top dashpot is calculated from the pile damping factor and
the difference in the velocities of the neighboring segments.
t
Fdij = cp (vi-1 - vi) (3.34)
The force of the bottom spring is:

b
F sij = ki+1 (ui - ui+1) (3.35)
The force of the bottom dashpot is:

b
F dij = cp (vi - vi+1) (3.36)
Figure 3.8.2.1b: Schematic of Model of Segment i (left) and Free-Body

Diagram (right)

3.8.2.3 Newton's Second Law for Acceleration Calculation
Using the external resistance forces, Rsij and Rdij, calculated at the end of a
previous time step, and the gravitational acceleration of the segment, g, it is
now possible to compute the acceleration of a pile segment, i, during the
current time step, j (see free body diagram in Figure 3.8.2.1b).
t t b b
aij = g + (Fsij - Fdij + Fsij - Fdij - Rsij - Rdij) / mi (3.37)
Of course, for a hammer or driving system segment, a similar equation

would result, except that no resistance forces would be present. Note that g
= gP for pile segment calculations and g = gH for hammer or driving system
segments. For the bottom ram segment and impact block of a diesel
hammer, the hammer’s pressure force would be a decelerating and
accelerating force, respectively.
As mentioned earlier, since version 2002, GRLWEAP allows for an input of

gravitational acceleration values, g H and gP, for hammer and pile. This
allows the user to modify the effect of weight, for example due to buoyancy
or pile batter. The mass effect of the ram, pile or any other system
component is not affected by the input of a gravitational acceleration
different from the standard value. Note that the effect of batter on the
impact velocity has to be considered primarily through modified inputs of
stroke and efficiency. Since 2010 GRLWEAP provides automatic
suggestions. As for the pile, if it is desired to construct a bearing graph that
does not contain the weight effect of the pile, then g P should be set to zero.
Except for long piles or those with a significant portion of their length
extending above grade, it is expected that the pile weight has an
insignificant effect on the results. Note that variation of g P along the pile
length is not possible. However, the offshore version allows for adding a soil
plug mass effect for a user defined plug length.
3.8.2.4 Corrector Integration
After the acceleration value has been calculated for a segment, its velocity
and displacement values are corrected by integration under the assumption
of a linearly varying acceleration:
vij = vij-1 + (aij + aij-1) t/2 (3.38a)
and
uij = uij-1 + vij-1 t + (2aij-1 + aij) t /6

2
(3.38b)
Since the displacements are now more accurately known than after the
t b
initial prediction, the spring forces F sij and F sij are recalculated. The
t b
changes of dashpot forces F dij and F dij are also recalculated. Thus, for the
calculation of the spring forces on the next lower segment, i+1, updated
force values are available.

3.8.2.5 Further Iterations
The process of calculation of forces, accelerations, and then displacements

can be repeated for the same time increment, with the newly computed a ij,
vij, and uij values taking the place of the previous prediction. Repeat
calculations would not be done if either the number of required iteration
steps had been exceeded (the maximum number of iterations is an input in
Options/ General Options/ Numeric) or if convergence of the velocities of
the top and bottom pile elements had been achieved. After convergence of
the pile variables, the resistance forces are calculated for the next interval
according to Section 3.7. In general, additional iteration steps do not lead to
a noticeable improvement of program performance and, since they have not
been used in correlation calculations, they are therefore not encouraged.
Experience has shown that smaller pile segments and/or smaller time
increments are more successful in improving the numerical performance of
the program than additional iterations.
3.9 Stop Criteria
It is not possible to predict the required analysis duration (or for how many
time steps an analysis has to be carried out) to assure accurate
computation for the permanent set. If the analysis runs longer than
necessary, undue computational effort is expended and round-off errors
may increase. If it is stopped too early, the computed permanent set may
be inaccurate (in easy driving too small).
The stop criteria had to be different between ECH and diesels because of
the diesel's particular requirements, primarily the need to analyze over a
sufficient time period for an accurate stroke calculation. For vibratory
hammers, a convergence of pile variables from cycle to cycle has to be
considered. For ECH, the following stop criteria are used (this is not
applicable for RSA):
A1: The analysis is run until the user-specified (Options/ General Options/
Numeric) elapsed time, tmax, has been covered. Of course, a short
user specified tmax may cause erroneous results. Therefore, tmax should
be specified cautiously, and comparative analyses should be run.
A2: If the user did not specify an analysis time tmax, the analysis will cover
an analysis time after impact of at least 3L/c (three times pile length
divided by wave speed) plus 5 ms or at least 50 ms. The analysis is
then stopped only when one or more of the following additional criteria
are met:
A2.1: The absolute value of the rebound (upward) velocity exceeds 20

percent of the maximum pile top velocity and 4L/c has been exceeded.
A2.2: The pile toe displacement has exceeded 100 mm (4 in). Since
this presents rather easy driving, not much can be learned from a

longer analysis, however, this means that the minimum calculated blow
count is 10 blows/m (3 blows/ft).
A2.3: The pile toe has rebounded to 80 percent of the maximum pile
toe displacement. (Such a rebound is sufficient to assure that the pile
will not penetrate deeper).
A2.4: No pile segment speed is greater than 20 percent of the

maximum pile top velocity and the pile toe has rebounded to 98
percent of the maximum pile toe displacement.
For 2-pile analysis, rebound checks are made on both piles.
For diesel hammers, elapsed time is counted starting 2 ms before either

impact or ignition, whichever occurs earlier. The analysis stops when
either:
B1: The user-specified elapsed time, tmax, has been covered. (See also
A1).Note that a very long analysis duration specified by the user may
last into a new downward cycle and produce erroneous results, which
may cause the message “Ram has downward velocity at end of blow”.
B2: If the user did not specify a time, tmax, the analysis will cover an
elapsed time of 3L/c + 5 ms or 50 ms, whichever is longer. The
analysis then stops only if at least one of the following two conditions
occurs:
B2.1: No pile segment speed exceeds 20 percent of the maximum pile

top velocity and
B2.1.1: The pile toe has rebounded to 80 percent of the maximum pile
toe displacement and the ram has reached a distance of at least 10
percent of the compressive stroke from the impact block.
B2.1.2: The pile toe has rebounded to 98 percent of the maximum pile
toe displacement and the ram has reached a distance of at least 20%
of the compressive stroke from the impact block.
For vibratory hammers, the user specified tmax is analyzed. Alternatively,

after the greater of 200 ms or 2L/c + 5 ms + 5 cycles have been analyzed,
the segment displacements of consecutive cycles are compared. Once they
converge or after at most 10,000 ms have passed, the analysis is finished.
Obviously, this implies that for very low hammer frequencies, only a few
cycles would be analyzed; for a 1 Hz vibratory frequency (60 cycles per
minute, representing an almost static condition), this would correspond to at
most 10 cycles. For the Smith algorithm, this is an extremely long analysis.
For an analysis with a good chance of convergence to a steady state pile
penetration, the hammer frequency should probably be at least 5 Hz.

3.10 Blow Count Computation - Non Residual Stress Analysis
For blow count calculations, the difference between the maximum toe
displacement, umt, and the average quake is calculated. The average quake
is:
qav = ∑ [Rui(qi)]/Rut (3.39)
where Rui and qi are the individual ultimate resistance values and quakes,
respectively, and Rut is the total ultimate capacity. A summation is made
over all elements from i = 1 to N+1 (N is the number of pile segments).
Resistance number N+1 represents the end bearing. The predicted
permanent pile set is then:
s = umt - qav (3.40)
and the blow count is:
Bct = 1/s (3.41)
It should be noted that for strongly variable quakes a residual stress

analysis may be a more accurate method of blow count computation.
For 2-pile analyses, umt is the lesser of the two pile toe maximum
displacements. However, this does not guarantee that the blow count is
calculated accurately for a 2-pile analysis. For this analysis option, the user
must carefully review the relative motions of both piles.
For two pile toe resistance values, only the primary pile toe is considered,
however, qav considers the resistance effect of the second pile toe.
For vibratory analysis the average pile penetration per unit time
corresponds to set per blow for impact hammers. The inverse of this value
is the penetration time per unit time (e.g. per second) and this is a value
that is often recorded for construction control.
3.11 Residual Stress Analyses (RSA)
3.11.1 Introduction
Primarily for reasons of computational economy, the Smith approach to

wave equation analyses makes two important simplifications.
 In the beginning of the analyses, it is assumed that the forces in

the pile and the soil are zero. GRLWEAP corrects this assumption
only to the extent that the helmet-hammer assembly and pile
weight are balanced by the static soil resistance. Since 2002,
GRLWEAP performs an accurate equilibrium check prior to
dynamic analysis. Earlier versions of the program only performed
a simplified analysis.

 At the end of the analysis, the pile starts to rebound. However, the
full rebound is not analyzed, and the final permanent set is
"predicted" by subtracting the average quake from the maximum
toe displacement. This approach assumes that the pile rebounds
to a stressless state and is therefore consistent with Smith's
simplifications.
There are many cases for which Smith’s simplified approach is satisfactory.
For example, if the soil exhibits little or no skin friction forces, the
conventional assumptions are justified. Another example is a pile which is
relatively rigid such that its elastic compression is small compared to the
soil quakes. Hery (1983) and Holloway et al. (1978) describe reasons for,
and calculation methods of, residual stress assessment.
In general, however, a pile does not completely rebound after the hammer
blow is finished. Often the toe quake is larger than the skin quake and
therefore, the toe tends to push the pile back up a relatively long distance.
As the shaft elements of the pile move upward during rebound, their
resistance first decreases to zero and then becomes negative until an
equilibrium exists between the upward directed (positive) resistance forces
at the lower portion of the pile and the downward directed (negative) shaft
resistance values of the upper pile. The pile is then at rest and compressive
forces are locked into pile and soil.
A large toe quake is not the only condition necessary for residual stresses
to occur in pile and soil at the end of a blow. Consider a very flexible pile
with a high percentage of shaft resistance. During the first hammer blow,
the pile's upper portion will move deeply downward due to the pile's high
flexibility. The shaft resistance will prevent a large pile toe penetration.
After the hammer ceases to load the pile head, the upper pile portion
attempts to elastically rebound a large distance, the toe only a short one.
The upper friction forces will turn negative and the pile will remain
compressed. The next blow will be able to drive the upper pile portion
deeper because the pile is pre-compressed and the downward upper
resistance forces help move the pile. At the end of the second blow, the
precompression in the pile may be greater than for the first blow and extend
deeper along the pile.
Eventually, all pile segments will achieve the same set, and pile
compression will no longer increase from blow to blow. (For very long and
flexible piles, it may take groups of blows to produce a converging
compression pattern.) Also, it is possible that pile sets per blow converge
towards zero (refusal) after initial blows produced a pile top set (but
probably no pile toe set). It is also conceivable that in very long piles both
tensile and compressive stresses remain after a blow is finished.
It is likely that the major portion of compressive soil resistance acts along
the shaft of the pile near its bottom. End bearing need not be present for
residual stresses to be locked in pile and soil.

For very long and flexible piles it may be difficult to decide whether or not
convergence has occurred in an analysis. For that reason, since 2002
GRLWEAP has allowed a user to input the number of trial analyses with the
default increased from 10 to 100. Also, the RSA blow count calculation now
relies on the trends of sets that groups of blows develop rather than the
difference of the sets of two consecutive blows. In this way, non-
convergence of RSA analyses is generally avoided.
3.11.2 Details of the GRLWEAP RSA Procedure
GRLWEAP undertakes the following computational steps in an RSA:
 After the first standard dynamic analysis is finished for one R ut

value, and displacement and static resistance values together
with the quakes are subjected to static analysis, the pile and soil
displacements and forces in static equilibrium (all velocities are
zero) result.
 A second dynamic analysis (which may be thought of as a

simulation of a second blow) is done with the displacements and
forces from the static analysis as initial values.
 Again a static analysis is performed after the dynamic analysis is

finished.
 After at least 3 repeat analyses, pile sets are computed as the

static pile top displacement of the present repeat analysis (or a
group of analyses if sufficient analyses have been performed) and
compared to the set from the previous analysis (or group of
analyses). If these set values compare within 0.1% the analysis is
finished. The analysis is also finished if the sets are very small
and tend to go towards zero (refusal) or if the maximum number of
trial analyses (input value) has been exceeded. Calculated set
values are included in the numerical output and the user is urged
to assure that the rather complex convergence analysis has
performed satisfactorily by reviewing this list of sets .
Further details of possible interest to the GRLWEAP user are:
 The computed static displacement vector is always normalized

such that the pile top displacement is always zero at the beginning
of an analysis. The subtracted value can be considered the pile set
if the analysis has converged, i.e. if the displacement pattern and
therefore the residual forces are the same from blow to blow.
Subtraction of the same pile top set from all segment
displacements is acceptable, because pile segment displacements
are relative values only. Pile and soil forces and the relative pile
displacements are not affected by this normalization. This

explains, however, why sometimes negative displacement values
appear near the bottom of the pile.
 The output includes the final displacement pattern, normalized

such that the top displacement equals the computed final pile set.
The maximum stresses listed in the extrema table and the final
summary table include residual stresses. The stresses remaining
in the pile after the impact event is finished are listed in the RSA
table following the extrema table.
The basic concept of RSA is to find the displacements and static soil
resistance values when the pile has completely come to rest, or in other
words, when a static equilibrium of the system is achieved. Theoretically, in
a dynamic analysis, the pile never comes to rest. It is therefore necessary
to interrupt the dynamic analysis once it has been ascertained that the pile
will not achieve additional penetration.
At the end of the dynamic analysis, for all N pile segments and N+1
resistance values, the final pile segment displacements and static
resistance values are saved.
ufi, i = 1,2,...,N (3.42)
and
Rsfi, i = 1, 2,...,N+1 (3.43)
The unknowns are the pile segment displacement, u si, and static soil
resistance values, Rssi, for which static equilibrium exists. For the static
equilibrium analysis, the pile-soil model is the same as in the dynamic
analysis, except that now the inertia forces and the forces in pile and soil
dashpots do not exist. The soil springs are still elasto-plastic and at the end
of the dynamic phase, a soil spring may be in any one of the following
situations.
 the spring did not go plastic and therefore loading and unloading
will occur on the same path (Figure 3.11.2a).
 the spring did go plastic and the soil resistance is the ultimate
resistance. The unloading will start from the point D and will follow
a path parallel to the loading line (Figure 3.11.2b)
 the spring did go plastic but started to unload. Further unloading

will occur on the same slope. If the ultimate soil resistance in
tension is reached, unloading will follow the plastic path (Figure
3.11.2c).

Figure 3.11.2: Resistance vs. Displacement Diagrams Showing End of
Dynamic (D) and Static (S) Analyses
 the spring did go plastic in compression, then in tension.

Thus,unloading will occur along the plastic line (Figure 3.11.2d).
A priori, it is not known which springs will become plastic and whether there
will be loading or unloading of the soil springs. The best formulation, linking
displacements and soil resistance values is
Rsi = Rsfi - (Rui/qi)(ufi - ui) (3.44)
with Rsi being subjected to the same ultimate limits as discussed earlier.
The mathematical solution of the problem involves a set of linear equations
subject to the conditions of elasto-plastic springs.
3.11.3 Additional Comments about RSA
There is no doubt that the RSA better approximates actual piling behavior
than the traditional approach which ignores the initial conditions of pile and
soil. A drawback of using the approach is the fact that many correlation
studies have been done without RSA. The magnitude of quake and/or soil
damping values, obtained from such studies, may need adjustment when
using RSA. For high resistance values, the accuracy of the RSA approach
depends heavily on the accuracy of the soil model. For example, the
relative magnitude of shaft resistance and end bearing and the relative
magnitudes of quakes may significantly affect stress and blow count results.
Even Smith’s simplifying assumption that loading and unloading quakes are
equal or that the static resistance is elastic-ideal plastic may cause
significant errors in RSA. Thus, before accepting potentially non-
conservative RSA results, it may be wise to perform comparative analyses
or use measurements to back up the calculations. At this time, the need for

RSA has only been proven for Monotube™ piles, but not for regular pipe
piles, H-piles or concrete piles. For very long offshore pipe piles,
indications are that RSA results are more realistic than non-RSA results.
3.11.4 RSA Restrictions
RSA cannot be run in conjunction with
 Two-pile analysis
 Two pile toe analysis
 Vibratory analysis (it practically does consider residual stresses)
 Piles involving slacks
In order to assure a well dampened behavior of the calculated pile motion

(measurements do indicate a well dampened behavior) it is recommended
to use the Smith-viscous damping approach rather than the standard
method (Options/ General Options/ Damping).
3.12 GRLWEAP Analysis Options
3.12.1 Bearing Graph
The most commonly used GRLWEAP analysis is the bearing graph

calculation. A total ultimate capacity is assumed and distributed on shaft
and toe as per input. The blow count is then calculated. A higher total
ultimate capacity value is chosen next and shaft and toe resistance are
proportionally increased to match the capacity; this is followed by the
dynamic analysis. Up to ten capacity values are analyzed in this way and
then capacity is plotted vs calculated blow count.
GRLWEAP also allows for an increase in either shaft resistance or end

bearing with the other resistance component held constant for the ten
capacities analyzed. These are then called constant end bearing or
constant shaft resistance bearing graph analyses, respectively.
3.12.2 Inspector’s Chart: Blow Count vs. Stroke
For diesel hammers, it is often required to adjust the driving criterion

according to the apparent stroke. Stroke of open end diesel hammers can
TM
easily be monitored using a Saximeter . Thus, it may be required to run
individual analyses with several fixed strokes in order to provide the field
inspector with a driving criterion for each apparent stroke. For simplification,
an inspection graph option was built into GRLWEAP which automatically
produces ten analyses with strokes increasing from a user specified
minimum value to the hammer’s rated stroke.
The Inpector’s Chart (IC) provides a relationship between stroke (equivalent

energy) applied and blow count required to achieve one ultimate capacity
value. This option is often done in conjunction with a Bearing Graph
analysis or a Refined Wave Equation Analysis. The IC analysis option

would not be meaningful for traditional mechanical hammers which are only
capable of operation with a single fixed stroke. However, modern hydraulic
hammers and diesel hammers can and/or should be operated at different
stroke or energy levels in order to control stresses. The option is particularly
useful for hammers which are difficult to control which means that a certain
stroke or energy level cannot be required and the inspector has to select
that blow count criterion that matches the actual stroke. For example diesel
hammers may respond to certain conditions, among them ambient
temperature, altitude, state of maintenance, fuel type and soil stiffness with
different stroke levels. Note that it is important that the actual hammer
stroke or energy level is known for a meaningful use of the IC. For example,
hydraulic hammers without internal kinetic energy monitoring or without
visible ram movement cannot be judged as to their energy output. Such
hammers should be equipped with the appropriate measurement device
(e.g., with the Energy Saximeter).
For diesel hammers caution is advised, because a high stroke is sometimes

an indication of preignition which increases the stroke while self cushioning
the ram impact and thus transferring less energy than a normally
performing hammer with lower stroke. Furthermore, high diesel hammer
strokes for a relatively low capacity may not be achievable and the IC would
show unusually high transferred energies if the combustion pressure, pmax,
were unreasonably increased to produce such a high stroke. For that
reason, the IC analysis option for diesel hammers works most reasonably
with a single hammer impact without adjustment of p max. However, the
experienced analyst may want to review the two stroke options available for
diesels: “Convergence of pressure with fixed stroke” and “Single analysis
with fixed stroke and fixed pressure” (see Options/ General Options/ Stroke
which is only accessible for diesel hammers.) In the IC analysis mode, the
former option will only reduce the pressure for low strokes and not increase
the pressure for high strokes for conservatism. Please note, since the IC
analysis options calculates blow counts for 10 different strokes, it is
performing fixed stroke analyses and the hammer setting (pmax level) has no
effect when pressures are adjusted for convergence. However, pmax has
some effect in the single drop case, because higher pressures add to the
energy transfer.
3.12.3 Driveability Analysis
This option calculates blow count, stresses and transferred energy vs pile
penetration without running separate bearing graph analyses for each
depth. In other words, the driveability analysis performs numerous bearing
graph analyses automatically for user specified pile tip penetrations. Input
consists of unit shaft resistance and end bearing values (since 2010 unit
end bearing plus toe area) obtained by static soil analysis along with soil
layer specific quake and damping values. In addition, so-called gain/loss
factors modifying the unit shaft resistance or unit end bearing values, can
be specified. These factors allow the user to model complete or partial loss
of soil setup, relaxation effects or the long term soil resistance. Up to five
gain/loss factors can be entered and analyzed, in effect providing for up to

five capacity values at every analyzed depth. Note that in order to
differentiate between the specific resistance losses of different soil layers a
soil setup factor will also be considered in the driveability analysis as
explained below. At the end of the analysis, the driving time can then be
estimated from calculated blow count and hammer blow rate for each
gain/loss factor.
An accurate static geotechnical analysis must be performed prior to

calculating blow count vs depth. Since 2002 several static analysis routines
were added to GRLWEAP and it is tempting to merely use these methods
for the calculation of shaft resistance and end bearing. However, the
analyst should be carefully reviewing the static analysis results. Details of
these static calculations are discussed in Section 3.13.
3.12.3.1 Gain/Loss Factors
Prior to performing a dynamic analysis, the static resistance has to be

estimated by geotechnical analysis of the soil. The result of this analysis is
the Long Term Static Resistance (LTSR). However, during pile driving the
soil properties change and the pile encounters the Static Resistance to
Driving (SRD). The conversion of LTSR to SRD is accomplished in
GRLWEAP by means of Gain/Loss Factors, fR, and Setup Factors, fS. While
the Gain/Loss factors control the absolute change of static soil resistance,
the Setup Factor controls the relative change of soil resistance among the
various soil layers. There are two different approaches which allow for the
calculation of SRD from LTSR. The standard GRLWEAP approach will be
discussed in this section. A second approach referred to as Friction Fatigue
is an Offshore Wave feature and is described in Appendix E.
For a particular soil type
LTSR = fS SRD (3.45)
if SRD is soil resistance occurring after the pile has been driven a certain
distance, called limit distance, LL, In theory, driving the pile a distance equal
to LL assures that SRD has been achieved. The LTSR will be occurring
some time after driving which is called the setup time, tS.
The GRLWEAP gain/loss and setup factor concept will be explained by

example. The simplest example would be a single soil layer, e.g. a clay,
with setup factor fS = 2.5. The reduction factor during driving would
therefore be fRD = (1.0/2.5) = 0.4, if we would want to reduce the LTSR to
the SRD to represent full resistance loss. If we would want to analyze the
restrike situation with full setup, fRD = 1.0 would be appropriate. For
incomplete setup we could also analyze f RD = 0.7. For each depth
analyzed, with the three gain/loss factors fGL = 0.4, 0.7 and 1.0 specified as
an input, a bearing graph would be calculated by the driveability analysis
with three ultimate capacity values, one bearing graph for each depth
analyzed. For each of these analyses, an appropriate end bearing
gain/loss factor could also be considered in the input.

Let us now assume that two soil layers exist, with different setup factors like
a clay layer and a sand layer with setup factor fS = 1.25. We would expect
that full loss of setup resistance would reduce the sand LTSR to an SRD of
1/1.25 or to 80% of its long term capacity. We would therefore want to use
fRD = 0.8 for the sand and fRD = 0.4 for the clay. This is a dilemma which
GRLWEAP solves by considering the gain/loss factor, fGL, specified by the
user to be consistent with the most sensitive layer. For less sensitive layers
the reductions of resistance would be proportionate to the ratio of setup
factors. Therefore, if we again analyze a gain/loss factor f GL = 0.4 (to cover
the set-up factor 2.5 of the most sensitive layer) and a gain/loss factor 0.7
(half loss of resistance of the most sensitive layer) and a gain/loss factor 1
for full setup (no loss of driving resistance) then the sand’s corresponding
reduction factors would be fRD = 0.8, 0.9 and 1.0 while for the clay we would
have fRD = fGL = 0.4, 0.7 and 1.0.
Mathematically, the capacity multipliers for the individual layers, f RD, are
calculated by GRLWEAP as follows. First, a relative soil/pile sensitivity, f S*,
is calculated from the set-up factors, fS.
fs* = (1-1/fs)/(1-1/fsx) (3.46a)
For the sand with fS = 1.25, fs* = (1 - 1/1.25)/(1 - 1/2.5) = 0.333 (the sand is
only a third as sensitive as the clay because it loses 20% when the clay
loses 60%) where fsx is the maximum set-up factor of all soil layers
analyzed (i.e. the setup factor of the clay, fS = 2.5, in our example). Next,
the friction reduction factor during driving is calculated from the gain/loss
factor, fGL, and relative soil/pile sensitivity.
fRD = (1-fs* + fs*fGL) (3.46b)
fRD = 1 - 0.333 + 0.333(0.7) = 0.9. Thus, when the clay is analyzed with
70% of its long term strength, the sand has 90% of its full capacity. This
capacity reduction factor is subject to variation as described under Section
3.12.2.2 below if setup time, tS, and limit distance, LL, are specified.
So far we have only considered shaft resistance setup. However, it should

be possible to vary the end bearing as the shaft resistance is varied at a
particular analysis depth. For example, the pile is driven through clay into a
silty sand. Since the silty sand layer is very dense, it has the potential to
build up negative pore water pressures and therefore high end bearing
values during driving, say 50% higher than the long term value. When
driving is over, the pore water pressures dissipate and then the toe capacity
goes back to the value which is known from static calculations. For
example, if the pile is driven through clay (set-up factor 2.5 in our example)
into a very dense, fine sand and silt, it may be reasonable to perform an
analysis with shaft gain/loss factors of 0.4 and 1.0 and respective toe
gain/loss factors of 1.5 and 1.0. The resulting two analyses at each depth
would consider the temporary dynamic (expected) and the long-term static
(restrike or worst-case driveability) situation, respectively.

The above examples are reasonable for impact driven piles. For vibratory
pile driving, sands and clays often behave very differently with sands losing
a very high and clays losing a very low percentage of their LTSR.
Suggestions are given in the “Table of Soil Set-Up Factors” (GRLWEAP
On-line Help).
3.12.3.2 Variable Set-Up
The above relationships are valid for a complete gain or loss of set-up as
shown in Figure 3.12.1. If the set-up period is interrupted by renewed
driving or if the loss of capacity due to driving is interrupted by a new set-up
period, then capacity losses or gains commence from an intermediate level.
GRLWEAP calculates for these situations, respectively, equivalent relative
dissipation energies or set-up times (Figure 3.12.2).
For driveability analyses which consider the variations of soil resistance as

the pile penetrates into the ground, it is also desirable to include soil set-up
effects that might occur during driving interruptions. When pile driving
resumes, the soil strength is lost depending on the energy dissipated in the
soil. To model this behavior, two relationships were developed: (a) the
capacity reduction factor due to the wait, fRW, as a function of set-up time,
tS; and (b) the capacity reduction as a function of the distance of driving
(which is related to energy expended on the soil remolding or pore water
pressure generation). The capacity reduction factor varies between the
inverse of the set-up factor and 1.0. When it is equal to the inverse of the
set-up factor, all of the set-up capacity of the soil has disappeared due to
the action of the dynamic energy of the striking hammer. When it is 1.0, set-
up has completely reappeared during the time following pile driving and the
capacity is then at its full long term level. For example, assume again a
clay with a set-up factor of 2.5. The capacity of an element embedded in
clay can therefore be as little as 0.4 times the full long term capacity. The
reduction factor can in this case vary between 0.4 and 1.0.
The capacity reduction factor due to the wait is defined as:
fRW = RUR / RUF (3.47)
where RUR is the capacity (of a pile/soil segment) reduced by the action of
the dynamic energy. RUF is the full ultimate capacity (achieved after full set-
up time) at the same segment. Skov and Denver, (1988), suggested that
the reduction factor is a function of set-up time, tS, and follows a log10
function:
fRW = 1/fS + A log10 (t / tB) (3.48)
with
A = (1 - 1/fS) / log10 (tS / tB) (3.49)

Remember that fS is the soil's set-up factor for the shaft resistance. Also,
the time, t, elapsed since driving was halted, has to be greater than the
reference time tB. This reference time has been set to 0.01 hours in
GRLWEAP, even though Skov et al. (1988) recommend a larger period
such as a day for a stable prediction of set-up strength. However, it is
reasonable to assume this set-up behavior occurs in short interruptions in
driving as well as during long wait periods as considered by the authors. A
one-day base time period would be outside of the time considered for such
driving interruptions.
For Any Segment I
Rui Rui
During Driving - Full Loss RUF During Waiting - Full Gain
Resume
Stop Driving
Driving
RUR
Limit Penetration Setup Time

Distance after Wait Time
Figure 3.12.1: Capacity vs Energy/Time for Complete Gain/Loss
Figure 3.12.2: Capacity vs Penetration or Time for Incomplete Gain/Loss
For the loss of resistance due to pile driving, a simple linear relationship has
been adopted, between distance driven and SRD. If the pile has penetrated
a particular soil layer a limiting distance, LL, it is assumed that all setup has
been lost. The limiting driving distance has been called a relative energy in
the past, because in its simplest form driving energy is resistance force
times the distance that the pile has been driven. Normalizing by division

with the average resistance leads to the limit distance. The limit distance,
LL, is a constant and may be considered a soil property (it is entered by the
user in the soil resistance profile). It has the dimension of length, i.e. m or ft.
Of course, the reduction factor can never be less than the inverse of the
set-up factor nor can it be greater than 1.
Important: variable setup works only for the first gain/loss factor, i.e., for the
first analysis of each depth. This calculation is not performed for the other
four gain/loss factors.
3.12.3.3 Notes and Hints on the Variable Set-Up Analysis
Entering the limit distance and setup time numbers in the S1 input screen,
the soil properties for the variable setup analysis are available. However, a
variable setup analysis will only then be performed when at least one
waiting time has been specified greater than 0.01 hours (base time for
setup calculations). Thus, when no driving interruption is specified in the D
screen, energy limit and setup time are ignored.
A variable setup analysis considers the remolding energy expended on the

soil. For each depth analyzed this energy is calculated as the distance
driven since the last waiting time. For example, it is assumed that at the
very bottom of the pile the soil has not been remolded while, at grade, it has
been remolded by the pile moving the full driven distance through the soil
since the most recent waiting time. The unchanged soil element at the
bottom of the pile will break down from full static resistance to the reduced
resistance as the pile is driven past the element. Only when the pile has
moved a distance equal to the limit distance will the former bottom soil
element be at its reduced static resistance.
A pile will therefore never experience complete resistance loss near the toe
for a variable setup analysis. This fact will be clearly apparent for a pile
with a high concentration of shaft resistance near the toe. To display the
effect of variable setup results, the same gain/loss factor can be used in the
second analysis that was analyzed in the first one.
A word of caution: The program always analyzes all depth values specified
in the D screen. The analysis results may indicate that, where a waiting
time was specified, the pile would refuse. Yet some distance below the
point with the waiting time, the pile may actually have a non-refusal blow
count. In reality, it would not be possible to drive the pile to this deeper
penetration because of the refusal, unless some jetting or other driving aids
were employed. Thus, casual inspection of the calculated blow counts vs.
depth, which misses the one depth result with refusal due to setup, may
suggest that the pile can be driven. In reality, it would only reach the depth
where the driving interruption and refusal blow counts occur.

Additional suggestions:
a. Variable setup analysis is only done for the first Gain/loss factor.
b. Variable setup analysis cannot be performed for Friction Fatigue

analyses (Offshore Wave Option).
c. GRLWEAP does not consider a variation of toe bearing with driving

energy or set-up time; the end bearing is either fully increased or fully
reduced as specified by the toe gain/loss factor. No variation of this
factor with soil layer properties is possible.
d.If no set-up time or relative energy is known (and the corresponding

inputs are left zero or blank), then the "variable set-up" analysis cannot
be performed. However, a constant loss or gain analysis is still
possible. Probably, the constant loss/gain analysis is as reasonable or
more reasonable than the variable one, because of the uncertainty of
limit distance, set-up time, and their variation with time.
e. If no set-up factors are specified, GRLWEAP assumes set-up factors of

1 for all layers. Gain/loss factors then produce uniform capacity gains
or losses in all soil layers along the pile.
f. There is no point in specifying set-up time if the limit distance is not

known or vice-versa. Entering one parameter and not specifying the
other leads to curious results.
g. GRLWEAP does not allow for a meaningful vibratory analysis with

variable set-up.
h. In a first effort, GRLWEAP users should attempt to perform hindsight

analyses matching the blow count behavior of known projects with well
documented hammer and soil data. Only after having gathered
enough experience should class A predictions be attempted of variable
set-up behavior of a hammer-pile-soil system.
i. As an aid in preparing input for a first trial analysis, the relative energy
may be estimated as 2 m (7 ft). This would mean for the GRLWEAP
approach that the soil would lose its set-up capacity after the pile has
been driven for approximately 2 m or 7 ft.
k. Set-up time may be as long as 6 weeks in some clays and as little as a

few minutes in sands. GRLWEAP assumes that the full set-up
capacity has been regained after a driving interruption greater than or
equal to the set-up time.
l. For reasonably accurate analysis results and driving time estimates

sufficiently many depths must be analyzed. This is particularly true
when modeling variable set-up and where soil layer changes or waiting
times are specified. However, even in uniform soil/driving conditions

increments of depths analyzed should not exceed 3 m (10 ft). On the
other hand, the maximum number of depths that can be analyzed is 98.
m.Variable set-up analysis is only performed on the analysis of the first

gain/loss factor. For all other gain/loss factors, no wait times or
energies are considered.
3.12.4 Second Pile Toe
Assume that a composite pile has to be analyzed. It consists of a large

concrete pile which at its toe is fitted with an H-beam tip of considerable
length. During driving, this pile experiences end bearing both at its concrete
bottom and at the H-pile tip. In order to facilitate the analysis of such a
situation both end bearing values can be specified. The sum of both end
bearing forces is the total toe resistance. Individual quakes and damping
factors can be specified for both toe resistance forces. For example, a
larger quake would be reasonable for the concrete toe, while a smaller
quake would be reasonable for the H pile tip. The second toe can be
specified when a Non-Uniform Pile is chosen in the P1 form. Nothing needs
to be done if the second toe resistance is to remain equal to zero.
As in a standard analysis, the set and blow count calculation for the Two
Pile Toe analysis uses the maximum first toe displacement (bottom of pile)
minus the average quake. The average quake, however, is calculated
under consideration of the second pile toe resistance and quake.
An RSA cannot be combined with a Two Pile Toe analysis.
3.12.5 Two-Pile Analysis
Possible applications of this option include a helmet with a long sleeve, a

mandrel and shell configuration, or a non-bonded, two-material pile. In
short, two piles should be analyzed where the stress wave is split into
parallel branches. The Two-Pile analysis cannot be combined with RSA or
driveability analyses.
The GRLWEAP Two-Pile option is flexible enough to accommodate the

following configurations.
 The second pile is directly driven by the helmet and is not attached
to the first pile either at its top or at any other segment.
 The second pile can be attached to any segment of the first pile.
Attachment of the two piles onto each other is accomplished by a spring

with slack, round-out and coefficient of restitution. The Users Manual
contains two examples.
Resistance distribution can be accomplished along both piles. Their relative

distribution numbers automatically assign different magnitudes of shaft

resistance to the two piles. For end bearing, the two-toe capability is utilized
in the P1 form.
Analyzing two piles is not complicated except that the blow count
computation becomes highly questionable. It is not simple to decide from
which toe displacement the set should be calculated. Currently, GRLWEAP
uses the smaller of the maxima of the two toe displacements. The user is
advised to carefully review the output, experiment with analysis durations
(Options/ General Options/ Numeric), and check the blow count calculation
to assure that the results are reasonable.
3.13 Static Geotechnical Analysis
3.13.1 Introduction
To simplify the soil model input process, two simple static analyses are
included in the GRLWEAP code. These analyses only yield an estimate of
static soil resistance. The user is urged to also try other methods (e.g.
computerized methods such as UNIPILE, DRIVEN and SPT97, the former
described by Fellenius, 1996 and the latter two made available by the
FHWA and the Florida DOT, respectively). Local experience may indicate
which methods of static pile analysis work and which do not work in a
particular geology. GRLWEAP’s analysis may or may not work well. One of
the reasons is that there are a large number of error sources in the soil
strength information obtained from borings and/or insitu test methods such
as SPT or CPT. Thus, it is virtually impossible to predict the accuracy
and/or precision of GRLWEAP’s static analysis methods compared with
static load tests. Basically, however, it should be assumed that any static
analysis predicts the long term pile bearing capacity. It has to be modified to
yield the static resistance to driving (SRD).
In addition to the static resistance values, the GRLWEAP static

geotechnical analysis methods also provide a help for dynamic parameters,
shaft damping and toe quake (toe damping and shaft quake are always
considered independent of soil or pile type). For the driveability analysis,
also rough estimates of the soil parameters pertaining to the soil
resistance’s gain/loss behavior are provided (setup factor, relative energy
and setup time).
Please review the method descriptions and application notes (Sections 3-

13.2 through 3.13.4) before accepting the results of these static
geotechnical analyses.
3.13.2 Soil Type Based Method (ST)
This method is intended as an aid in the input process for both bearing
graph and driveability analyses. For bearing graph analysis, it calculates the
percentage of shaft resistance and the shaft resistance distribution, for
which it selects reasonable dynamic soil parameters based on a very basic
soil description and classification. As with all of such approximate

calculation or estimation methods, the user should become familiar with the
basic concept of static soil analysis and its limitations and perform
comparison analyses using other methods to avoid serious errors. With
simplifying assumptions, the method uses information from Bowles and
Fellenius contained in Hannigan et al. (2006).
For Non-Cohesive soils:
The program applies the β-Method (Effective Stress Method). With this
method, the unit shaft resistance is:
qS = β pO (3.50)
with
β= The Bjerrum-Burland beta coefficient (earth pressure coefficient

times the tangent of the friction angle between pile and soil) and
po = Average effective overburden pressure along the pile shaft.
The unit toe resistance is:
qt = Nt Pt (3.51)
where:
Nt = Toe bearing capacity coefficient.

Pt = Effective overburden pressure at the pile toe.
The method
 converts the soil classifications of Tables 3.12.2a to soil unit
weight, β-value, and Nt-value,
 calculates the overburden pressure (under consideration of
buoyancy, thus the water table depth must be provided in the
input),
 with the β and Nt values of the table finds the unit shaft resistance
and end bearing and
 subjects these values to the limits in Table 3.12.2a.

Table 3.12.2a: ST Analysis Parameters for Non-Cohesive Soils
Soil Type SPT Friction Unit β Nt Limit (kPa)

N Angle Weight
3
deg. kN/m qs qt
Very 2 25 – 30 13.5 0.203 12.1 24 2400

Loose
Loose 7 27 – 32 16.0 0.242 18.1 48 4800
Medium 20 30 – 35 18.5 0.313 33.2 72 7200
Dense 40 35 – 40 19.5 0.483 86.0 96 9600
Very 50+ 38 – 43 22.0 0.627 147.0 192 19000
Dense
The user can also use the SPT N-values (corrected for the effect of
overburden pressure) given in the following table to find the corresponding
soil classification. (However, if the N-value is known then the more detailed
SA method may be used instead of ST.)
For Cohesive Soils:
For cohesive soils, the ST method applies a modified α-method (total stress
method). The calculation steps are
 From Table 3.12.3b and the given soil classification find the unit
weight, unit shaft resistance and unit end bearing.
 From unit weight and depth of water table (input) find the
overburden pressure (in case there are lower non-cohesive layers
for which the β method needs to be applied.
Table 3.12.2b: ST Analysis Parameters for Cohesive Soils

Soil SPT Unit
qu qs qt
Type N Weight
3
kPa kN/m kPa kPa
Very Soft 1 12 17.5 3.5 54
Soft 3 36 17.5 10.5 162
Medium 6 72 18.5 19 324
Stiff 12 144 20.5 38.5 648
Very Stiff 24 288 20.5 63.5 1296
Hard 32+ 384+ 19 - 22 77 1728
3.13.3 SPT N-value Based Method (SA)
The method is based on SPT N–value and soil type and only available in
conjunction with the Variable Resistance Distribution option, however, for

either Bearing Graph or Driveability Analysis. Since Version 2010 friction
angle and/or unconfined compressive strength can also be entered in the
SA window. Direct input of unit shaft resistance and end bearing is also
possible if a soil type “Other” is to be specified. This mode of input can also
be helpful to enter resistance values for rock.
The SPT N-value based method presented here does not use corrected N–
values as per FHWA recommendations (Hannigan et. al., 2006); however, it
limits N to at most 60. On the other hand, it is strongly recommended that
energy measurements be taken during SPT testing and that the N-value be
adjusted to the N60 value. In effect, this is a normalization which increases
the N-value for hammers with high transfer efficiency (greater than 60%)
and lowers them for poorly performing hammers (those with transfer
efficiencies less than 60%). The SPT Analyzer measures the transfer
efficiency of SPT hammers.
The method does not make recommendations for rock. As mentioned for
“Other” soil types, the user must input unit shaft resistance and end bearing
values. The user can also input the depth of the water table relative to
grade and an overburden causing a non-zero effective stress at grade.
As a basis for the calculation of several of the following quantities, the

vertical effective stress is calculated first, as follows:
Step 1: Find the soil’s unit weight (γ) based on Bowles (1977).
Step 2: Find the vertical effective stress, σv’, in the layer based on the
overburden on the layer, layer thickness, γ from Step 1, and the water table
depth.
A: Shaft resistance for sands and gravels
Step A1: Find relative density, Dr, from Kulhawy (1989 and 1991).
Step A2: Find friction angle, φ’, based on Schmertmann (1975 and 1978).
Step A3: Assume the pile-soil friction angle as δ = φ’.
Step A4: Find the earth pressure coefficient at rest, k o, based on Dr,
according to Robertson and Campanella (1983)
with (1 - sinφ’)/(1 + sinφ’) < ko < (1 + sinφ’)/(1 - sinφ’)
Step A5: Calculate friction: qs = ko tan δ σv’ with qs ≤ 250 kPa
Notes: (a) Depending on the grading of a sand and its coarseness, the
calculations may be slightly modified. (b) If friction angle is entered in lieu of
N-value, skip steps A1 and A2.

B: Shaft resistance for clays
Step B1: Find the friction angle from φ’= 17 + 0.5N with φ’ ≤ 43 degrees.
Step B2: Define the pile-soil friction angle as δ = φ’.
Step B3: Find the overconsolidation ratio (OCR) from N and σv’ [kPa]
OCR = 18N/σv’.
Step B4: Find the normally consolidated and earth pressure coefficient
according to Jaky (1944)
knc = 1 - sin φ’
Step B5: Find the earth pressure coefficient at rest as

½
ko = knc (OCR)
with (1 - sinφ’)/(1 + sinφ’) ≤ ko ≤ (1 + sinφ’)/(1 - sinφ’)
Step B6: Calculate the unit shaft resistance from

qs = ko tanδ σv’
with qs ≤75 [kPa]
Note: if the unconfined compressive stress qu is entered in lieu of the N-

value, the program will calculate adhesion values according to Tomlinson
(see Hannigan, 2006).
C: Shaft resistance for silts
Step C1: Use the friction angle φ’ from Step A2 if it is non-cohesive or from
Step B1 if it is cohesive.
Step C2: Find the Bjerrum-Borland β coefficient according to Fellenius

(1996) by linear interpolation.
β = (φ’ - 28)(0.23/6) + 0.27
with 0.27 ≤ β ≤ 0.5
Step C3: Calculate qs = β σv’,

with qs ≤ 75 kPa (cohesive), qs ≤ 250 kPa (non-cohesive).
Note: if the unconfined compressive stress q u is entered in lieu of the N-

value, the program will calculate adhesion values according to Tomlinson
(see Hannigan, 2006).
D: Unit end bearing for sands and gravels
Step D1: Calculate the unit end bearing based on the uncorrected SPT N-
value from
qtoe = 200 N [kPa],
with qtoe ≤12,000 kPa.

If friction angle has been directly entered, find corresponding N-value from
Bowles in Hannigan, 2006 and then calculate as shown.
E: Unit end bearing for clays
Step E1: Calculate the unit end bearing based on the uncorrected SPT N-
value from
qtoe = 54 N [kPa]
with qtoe ≤ 3240 [kPa].
If qu has been directly entered calculate unit end bearing as 4.5 qu
F: Unit end bearing for silts
Step F1: Find friction angle φ’ from Step A2 if it is non-cohesive or from

Step B1 if it is cohesive. (or use directly entered friction angle).
Step F2: Find the toe capacity coefficient, Nt, according to Fellenius (1996)
by interpolation.
Nt = (φ’ - 28)/0.3 + 20
with 20 ≤ Nt ≤ 40
Step F3: qtoe = Nt σv’

with 20 ≤ Nt ≤ 40 and qtoe ≤ 6,000 kPa.
3.13.4 The CPT Method in GRLWEAP
3.13.4.1 Introduction
Cone penetration tests are semistatic and resemble, though at a much

smaller scale, a pile. A variety of penetrometers such as mechanical and
electrical ones have been developed and there are penetrometers in use
which are not of standard size. The preferred Dutch Cone configuration has
2
a cone tip area of 10 cm and a cone angle of 60 degrees. GRLWEAP’s
method for calculating pile unit friction, fs, and unit end bearing, qt,
programmed in GRLWEAP assumes that the cone tip resistance, q c, and
the cone’s sleeve friction, qs, have been measured with such a standard
cone. The soil type determination is based on Robertson et al (1986) and
the resistance calculation is as proposed by Schmertmann, 1978.
3.13.4.2 Data Import
CPT data can only be imported into GRLWEAP from a text file. The
file format must meet following requirements (see also example in
Table 3.13.4.1).
a. Titles or comments should be placed at the beginining of the file and the
number of title and/or comment rows is an input to the program; The
program skips that many lines before beginning to read the numerical
data.

b. CPT data must consist of at least 3 number columns, containing in
order: depth, tip resistance, qc, and sleeve friction, qs.
c. Additonal columns of data such as pore water pressure are ignored;
d. The following combination of units will be recognized if as such defined

in the column headers.
 SI: Depth in m, both tip and sleeve resistance in MPa;
 SI: Depth in m, qc in MPa and qs in kPa;
 English: Depth in ft, both tip and sleeve resistance in tsf.
An additional input is penetrometer type (Electronic or Mechanical), which

serves to select the appropriate design curves.
Note: Since the CPT based resistance computation requires averaging the
data over certain ranges, smaller cone data depth increments are highly
recommended for better accuracy. Also at least five input depths (rows of
data) are required. The program checks and modifies if necessary the
depth increments using the following procedur
 First the average depth increment is found based on the imported CPT
data:
Average depth increment = Maximum depth / number of rows of data;
 If the average depth Increment is larger than 0.8 ft (0.25 m), the program
prompts a warning and increases the number of data points by
interpolation of the CPT data at a depth increment of (0.3 ft) 0.1 m;
Note: It is recommended that the user manually inserts as many rows of

data as are needed to make the depth increment 0.8 ft (0.25 m) before
importing the data.
Table 3.13.4,1: Example of the top portion of a CPT text file with 3 comment
lines and MPa units for both resistance values.

3.13.4.3 Soil Classification
The first step in the resistance calculation is based on the paper by

Robertson et al., (1986) with some modifications. This classification is a
necessary step in the procedure to calculate the resistance values and
determine recommended soil parameters such as quakes, damping factors
and soil setup related parameters. The friction ratio is calculated from q s /
qc. (sleeve friction divided by cone resistance).
Figure 3.13.4.1: Soil Classification Chart of Robertson et al, (1986)

Table 3.13.4.2: Soil Classifications
Soil Description corresponding to
Hannigan et al. (2006) to SA Method
Zone Soil Behavior Type
Poorly graded fine

1) sensitive fine grained sand
2) organic material Peat
3) Clay Clay
4) silty clay to clay Clay
5) clayey silt to silty clay Cohesive silt
Split between 5)
6) sandy silt to clayey silt and 7)
7) silty sand to sandy silt Cohesionless silt
8) sand to silty sand Sand
9) Sand Sand
10) gravelly sand to sand Well graded sand
Poorly graded fine
11) very stiff fine grained sand
12) sand to clayey sand Sand

3.13.4.4 Resistance calculation
(Distribution of friction and toe bearing) is based on Schmertmann, 1978,

An additional assumption is a uniform pile. This simplification has been
proposed by Schmertmann and since unit resistance is the result of this
calculation procedure and since the pile surface area will be as per user
input, the error is considered immaterial. Additonal inputs affecting the
results include:
 Pile material: steel, concrete and timber;

 Pile average diameter or width, B, for average depth D to B ratio;
 Pile toe size is used to determine the averaging range for toe
resistance calculation;
 Unit resistance limit based on a maximum q c of 15 MPa.
Unit shaft resistance for cohesive soils:
fs = α q s
where:
α = ratio of pile to sleeve friction in cohesive soil; a function of qs and pile
material (Schmertmann 1978).
qs = unit sleeve friction
Unit shaft resistance for cohesionless soils:
fs = kr K qs
where:
K = Ratio of unit pile shaft resistance to unit cone sleeve friction
(Schmertmann, 1978) as a function of depth, Z, penetrometer type and pile
material.
qs = unit sleeve friction.
kr = Z/8B for Z = 0 to 8B.
kr = 1 for Z ≥ 8B.
B = Pile width or diameter.
Note: In GRLWEAP’s CPT routine, Schmertmann’s curves for steel pipe
piles are used for all steel piles and those for square concrete piles are
used for all concrete piles.
fs ≤ fs, lim the unit shaft resistance limit entered by the user (default is 150
kPa)
Unit toe resistance for all soil types:
qt = ½ (qc1 + qc2)
where:
qc1 and qc2 are averages of unit cone tip resistance below and above pile
toe as per Schmertmann, 1978.
qt ≤ qt,lim the unit toe resistance limit entered by user (default is 15 MPa).

3.13.5 The API Method in GRLWEAP (Offshore Wave Version)
The method is based on API (1993). Note that this is an approximate

method and that API recommends instead using high quality soil strength
information where available. Also, this method is specifically applicable to
pipe piles.
Soil strength input for GRLWEAP’s routine is undrained shear strength for
cohesive soils and a general density classification for cohesionless soils.
Unit Shaft Resistance for cohesive soils:
fs = α c
where:
α = a dimensionless factor; it can be computed from:
-0.5
α = 0.5 ψ for ψ ≤ 1.0
-0.25
α = 0.5 ψ for ψ > 1.0
α ≤ 1.0.
ψ = c/po’
po’ = effective overburden pressure
c = undrained shear strength of the soil, which is an input
Unit shaft resistance for cohesionless soils:
fs = K po’ tan δ
where (see also Table 3.13.5.1):
K = dimensionless coefficient of lateral earth pressure (ratio of horizontal to
vertical normal effective stress). K = 0.8 for unplugged. K = 1.0 for
plugged. User can indicate if it is plugged in the program. For fully
displacement piles, user should indicate plugged to use K = 1.0.
δ = friction angle between the soil and pile wall.
fs ≤ fs, lim the unit shaft resistance limit.
Unit toe resistance for cohesive soil types:
qt = 9 c
with the c being the undrained shear strength.
Unit toe resistance for cohesionless soil types:
qt = po’ Nq
where (see also Table 3.13.5.1):

Nq = is a bearing capacity factor.
qt ≤ qt,lim the unit toe resistance limit.

Table 3.13.5.1: Design Parameters for Cohesionless Soils (API, 1993, p67,
Reproduced courtesy of the American Petroleum Institute)
3.13.6 Comments on GRLWEAP’s static formula methods
Static formulas for pile capacity determination are generally inaccurate for a
variety of reasons. For example, soil strength from N–value and soil type is
always only an estimate because SPT N–values are inherently inaccurate
and soil type information is subjective and the pile driving process itself
changes the properties of the soils and, therefore, affects both long term
soil resistance and SRD. Moreover, different physical, chemical or
geological conditions will produce different relationships between in-situ test
results and unit resistance values. Program users are, therefore,
strongly advised to always check the friction and end bearing values
that the program calculates both by comparing with other methods
and using any additional information, most notably local experience,
that might be available.
Not only pile driving changes the soil properties. Pile material has an effect
on the shaft resistance and effects like predrilling or jetting, an oversized
toe plate, driving of nearby piles causing heave and densification, group
effects, time effects like setup and relaxation, variable water table elevation,
excavations or refilling around and in the neighborhood of the pile, and
many other phenomena have a significant effect on shaft resistance and
end bearing.
GRLWEAP’s static geotechnical analysis methods should merely be seen

as an aid for the program user in estimating very basic soil resistance input
parameters. When performing the soil layer input, the program also displays
the calculated capacity and the shaft resistance. This additional information
may be used as a check on how reasonable the basic assumptions are and
whether or not the intended pile capacity can indeed be achieved. Again,
this capacity value should not serve for design purposes.

The total capacity of the pile is unit shaft resistance times shaft area plus
unit end bearing times toe area. The shaft area is based on the perimeter
values that the user inputs. Normally for H-piles, perimeter is computed by
the 4 sides of the piles. An argument could be made for using 6 sides, but
that assumption is highly uncommon. For the open ended pipes, the
question of internal friction is difficult to answer. It would be expected that
an unplugged pile (the soil remains at its location, i.e., it does fill the pile
and does not move with the pile – the cookie cutter effect) has some
internal soil resistance. However, unless diameter to embedment is
relatively large, the effective stresses will be relatively low inside the pipe
and the driving process will reduce the internal friction. Thus for most
unplugged analyses only partial internal friction is normally considered (it
can be modeled in GRLWEAP by increasing the perimeter value over that
length of the pile where internal friction is expected (e.g. on an internal
driving shoe which is an increased pipe wall thickness at constant outside
diameter). A case could be made for internal friction acting over 10 pile
diameters if the pipe wall thickness is uniform (please also note that API
makes recommendation regarding friction calculations in the plugged and
unplugged cases).
For the toe area, the user must determine whether or not plugging can
occur for open profiles. In very dense sands or during restrike testing after
a long waiting time, plugging may be expected unless the pile diameter is
very large (say greater than 900 mm or 30 inches) or the penetration into
the bearing layer is very shallow (say less than 3 diameters). Since H-piles
are normally relatively small (typically less than 350 mm or 14 inch) square,
the fully plugged area is usually assumed for end bearing calculations. In
general, the GRLWEAP’s default value for the pile toe area is that of the
closed end condition. It is therefore extremely important that the users
carefully review and possibly correct the pile toe area input. In
addition, it is also strongly recommended to perform optimistic
(unplugged) and pessimistic (plugged) driveability analyses to
establish lower and upper bound driving resistance values.
Due to the simplicity of GRLWEAP’s static geotechnical calculation

methods, effects of pile size, pile non-uniformity (such as a tapered pile
which may have a relatively high shaft resistance), influence of upper
lubricating soils on lower soil layers, the effect of pile material on the
friction, and many other influences normally affecting friction and/or end
bearing values were not necessarily considered in detail. Users should
therefore adjust the result based on the recommendations in the literature
or their own experience and judgment when these methods are used.
The user must also consider that the soil resistance values, calculated by
the static analysis, represent a long term pile capacity. For both bearing
graph and driveability analyses, if they are to represent the pile installation
conditions, both setup and relaxation effects must be considered.

3.13.7 Consideration of Pile Inclination in Static Soil Analyses
An inclined pile driven through a certain soil layer is in contact with a larger
surface area than a vertical pile. On the other hand the unit resistance is
most likely somewhat lower. In general it can be assumed that the total
shaft resistance acting on an inclined pile in a certain layer is the same
whether the pile is inclined or not. However, an inclined pile of the same
length as a vertical pile will not penetrate as deeply as the vertical one.
Thus, for a given pile length the pile inclination reduces the total vertical pile
penetration (Figure 3.13.6.1.)
If the pile inclination has been entered then these length and associated
resistance factors have been considered in the static soil analysis tools (ST,
SA, CPT and API). As a consequence, whenever the pile inclination is
changed, the users must repeat the soil resistance calculation by reentering
the particular analysis method chosen. Of course, the same is true if pile
penetration (for bearing graph analyses), pile type or pile profile are
changed.
Layer 1: Soft Clay
Layer 2: Medium Dense Sand
Layer 3: Stiff Clayer
Layer 4: Dense Sand
Figure 3.13.6.1 Vertical and Inclined Piles of the Same Length
Note that although the static soil analysis methods consider the actual
inclined vs. vertical penetration depth, the calculation of resistance at the
same vertical depth is identical for vertical and inclined pile.
3.13.8 Static Bending Stress Calculation of Inclined Piles
This option is only available in the Offshore Wave version.

When pile is inclined, supported by a jacket or template and the hammer is
guided by an offshore lead which, in turn, is guided by the pile, then it is
necessary to consider the bending stresses caused by the hammer weight
plus the pile section extending above the pile support. Because this option
is only available for GRLWEP’s offshore version, it is assumed that the pile
is a pile of constant outside diameter. The cross sectional area, A, wall
thickness, t, diameter, D, and specific weight, γ, of the pipe pile are,
therefore, know from the pile profile. This then allows for a calculation of the
bending moment due to pile weight, the moment of inertia and section
modulus. However, the following additional input is required (see also
Figure 3.13.7.1).
Wh Total hammer weight (Sum of all weights acting on pile top

including helmet weight and potentially a portion of the lead
weight)
hCG Center of hammer/helmet gravity (The distance from pile top
to the Center of the Gravity of hammer while the hammer sits on
top of the pile)
β Pile inclination angle (the angle between the axis of pile and
vertical direction)
Figure 3.13.7.1: Definition of static bending analysis parameters
Note: The following calculation assumes that the highest bending stresses
occur at the support point; bending stresses below that point are not
considered.
The static bending moment acting at a cross section at a distance y from

the pile top (without consideration of deflection) can be computed as
follows; first the shear force distribution at any point y from top is:

𝑦
𝑉(𝑦) = (𝑊ℎ + ∫0 𝛾𝐴𝑑𝑥 ) × sin(𝛽)
And the bending moment is:

z
M = Wh × hCG × sin(𝛽) + ∫0 V(y) dy
Bending caused by additional normal stresses require that deflections are

known. To compute the deflection, it is assumed that pile at the support
point is fixed and the angle of the pile axis at the support point is β.
The total deflection at top can be calculated from:

0
𝑀 𝑧 𝑑𝑧
𝛿= ∫
𝐿𝑏 𝐸𝐼
where: Lb is the pile length from support point to pile top.
Using the segments of the dynamic model, a numerical procedure is then

used to calculate shear, bending due to hammer and pile weight and
deflections due to bending including the static axial forces. Dynamic forces
are neglected owing to the shortness of the stress wave (both as far as time
and length).
Since deflections increase due to the normal forces, iterations are

performed until convergence is assured. Convergence means that the
system is stable. The following convergence criterion has been included.
𝛿 − 𝛿𝑝
| | < 0.1%
𝛿𝑝
where δ and δp are the deflections of the current and previous iteration
step, respectively. The maximum number of calculation iterations is 100. If
convergence is not achieved within that number of iterations, then a
warning is issued. It is also expected that the stresses will be excessive in
that case.
A word about the stress calculation and output should be added. If static
bending stresses are calculated for inclined piles, the Numerical Results,
Bearing Graph, Driveability and Stress Maxima Range Summary Tables
include Compressive and C+B stresses which are, respectively, the
calculated dynamic compressive stress and the bending compressive
component plus dynamic compressive stress. Dynamic tension stresses
and the dynamic tension plus bending tensile stresses are not listed in
either Numerical Results or Bearing Graph/Driveability output. Tension
stresses can, however, be back-calculated from the tension forces listed in
the Numerical Results if Normal Numerical Output option is selected
(Options->General Options->Output) and, as far as bending is concerned,

from the difference between compressive dynamic and bending plus
dynamic stresses. The Stress Maxima Range tables (see Section 5.5) for
fatigue analysis do contain the tension stresses.
Questions arose whether or not the normal forces due to the hammer-lead-
driving system weight were included in the stress calculation. The answer is
“No” and there are two reasons for not adding the static hammer-lead
driving system weight to the dynamic and bending stresses. First, as long
as the gravitational acceleration of hammer and pile are properly input, the
dynamic analysis already includes the weight effect of hammer (ram plus
assembly), helmet and pile. Considering them again would double that
effect. Secondly, while the free riding leads may add bending due to its
weight component perpendicular to the pile axial direction, it is expected
that most of the lead weight would be supported by the crane. And even if
the weight of the leads were instead fully supported by the pile, during the
impact the pile would be rapidly moving away from the leads and only later,
during rebound, would it again be supported by the pile. At that time,
however, the critical situation of maximum compression at the support point
would have passed. Note that the axial weight effect of the leads is the
same as the effect of the assembly. Note also that neglecting the lead’s
axial weight effect on the soil prior to impact is conservative as far as blow
counts are concerned.
3.14 Program Flow
3.14.1 Bearing Graph
 After accepting hammer, driving system, pile and soil input (and
potentially calculating static resistance values in the static
geotechnical analyses), GRLWEAP sets up a lumped mass model
for hammer, driving system, and pile and distributes the skin
friction of the first ultimate capacity value. A description of the
complete model is then printed.
 Next the analysis time increment is computed, followed by an

equilibrium analysis which determines whether or not there is
enough resistance to balance the dead loads (hammer assembly,
helmet, pile weight). If there is not enough resistance, the analysis
is skipped and a 0 blow count is output.
 Next the actual wave equation analysis is performed for the first
capacity or depth value. For diesel hammers, the rated hammer
stroke is assumed if the standard stroke option has been selected.
 At the end of the analysis, for RSA an equilibrium analysis is

performed and the analysis is repeated until RSA pile sets have
converged. For diesels, the calculated up stroke is compared with
the down stroke. If they are not equal within the selected stroke
convergence criterion, the analysis is repeated with the calculated
up stroke as a down stroke (except for iteration on pressure for

which the combustion pressure Pmax is adjusted. For further
details, see the section on “Diesel Analysis Procedure”).
 At the end of an analysis, and after diesel stroke and/or RSA

convergence have occurred, GRLWEAP saves on disk extrema
tables and variables vs. time tables, depending on the user chosen
output option. On the monitor screen, a line of results is displayed.
 The next ultimate capacity value is now distributed along the pile
and at the pile toe and then a new analysis cycle is performed.
 If for one analysis a refusal blow count is calculated, the bearing

graph calculation is finished. (For this reason, the user should
enter capacity values in increasing order). An exception is the
situation in which the previously analyzed capacity was relatively
low. Then an additional capacity is interpolated and analyzed.
 When all ultimate capacity values have been analyzed, the

calculated stress extrema, transferred energies, and blow counts
are saved in the summary table file. The analysis process is then
finished, and the user should now click on the output icon and
check the numerical output. Be sure there are no messages in
the numerical output that would indicate an unusual program
performance (e.g. numerical instability, or hammer did not run). If
satisfactory input and output have been ascertained, the user
should choose to print and plot the bearing graph, print all or
portions of the numerical output, and if desired, generate plots of
hammer and/or pile variables versus time.
3.14.2 Driveability
 Driveability involves first of all a static soil analysis, which may be

done either manually, using commercial software, or using the
GRLWEAP static analysis options (ST, SA, CPT or API). If the
static geotechnical analysis is not done with the GRLWEAP
routines, then the depth, unit shaft resistance and unit end bearing
values can be imported into the S1 soil resistance form using
Window’s copy and paste features (Edit/ Paste Special).
 In a first step, for the depth to be analyzed, the program

determines the temporary pile length (it may be less than the final
pile length as per the Depth Table, i.e. the D input form). Then the
lumped mass soil model is set up. From the D-table also the
waiting time is checked and from it a determination of the status of
soil setup is determined. Also hammer and cushion properties are
checked based on the D-tables modifiers.
 The dynamic analysis initiates with a calculation of the long term

ultimate pile capacity and its resistance distribution for the first
depth.

 In addition to unit shaft resistance and unit end bearing, based on
the depth of penetration analyzed the following additional
parameters are calculated as follows:
 The shaft quake and damping values are averaged over the
individual segment length (in case a soil layer change happens
at a segment interface) to determine for each segment the
appropriate value;
 The soil setup factors, limit distance and setup time are
determined for each segment;
 The toe area which is then multiplied by toe unit resistance and
toe gain/loss factor to yield the end bearing
 Toe damping and quake values are determined by

interpolation.
 For the first gain/loss factor the SRD is calculated considering

the variable setup based on the waiting time and driving
distance since the last waiting time. For all other gain/loss
factors, the shaft resistance is calculated based on setup factor
and gain/loss factor only.
 A wave equation analysis is then performed subject to diesel

hammer and RSA convergence, if applicable. A single output line
is displayed for this first set of shaft and toe gain/loss factors. For
the remaining gain/loss factors shaft resistance and end bearing
are then calculated and analyzed.
 After all gain/loss factors have been analyzed for the same depth,
the program repeats the process of calculating temporary pile
length, ultimate capacity and other resistance values for the next
depth starting with the first gain/loss factor. Again a single output
line is displayed for this first gain/loss factor at the new depth
analyzed.
 All depths specified in the D-form have been analyzed, GRLWEAP

organizes the bearing graph results and generates a final result
table of blow counts, stress extrema, transferred energy and
stroke (equivalent to hammer energy) for each set of shaft and toe
gain/loss factors. These results are then saved on disk.
 As a next step, the user should inspect the numerical output and
print all or portions of it. The “vs depth” table can then be output in
printed or plotted form. This is the driveability result.
 If extrema table output is desired then the output option (Options/

General Options/ Output) should be set to normal (it is

automatically set to minimum because of the potentially large
volume of data) and repeat the analysis. If Variables vs time (e.g.
a plot of pile top force and velocity) is needed, then it should be
noted that GRLWEAP will only save the Variable vs Time data for
the last depth analysis. Thus, the D-table should be shortened to
allow for calculation of the desired depth in the last analysis.
3.14.3 Inspector’s Chart
 The first analysis is begun like the bearing graph analysis, with the
ultimate capacity distributed in the same manner. For the first analysis,
the stroke is either the user specified input value or an automatically
selected value. For diesel hammers, the program then iterates with
pressure adjustment or competes the single impact stroke option (see
note below).
 After the first analysis is finished, the program repeats the wave
equation for second and later stroke values always with the same
capacity and resistance distribution until 10 strokes (or energy levels,
or frequencies) have been analyzed. The user proceeds with checking
the input data in the numerical output and producing a stroke versus
blow count output in numerical or graphical form.
Note for Inspector’s Chart analysis for diesel hammers: For diesel
hammers, the hammer stroke analyzed generally is different from the
hammer stroke normally calculated for the capacity analyzed and the
combustion pressure of the hammer data file. Let us call this stroke the
“normal” stroke. The reasons why the actual stroke in the field is different is
not always clear. A low stroke generally can be attributed to a low
combustion pressure. A high stroke, however, may either be due to very
good hammer performance or, in the case of preignition, very poor hammer
performance. High strokes, therefore, pose a dilemma for the wave
equation analyst. For the Inspector’s Chart calculations, GRLWEAP offers
the user two different stroke options that are conservative when analyzing
high strokes.
(A) The default option is identical to the Single Stroke Option (Options,
General Options, Stroke). It only applies one impact, and no
iterations will be performed on combustion pressure. As a result, for
analyzed strokes less than the normal stroke, the rebound stroke
will be higher than the analysis stroke. For analysis strokes above
the “normal” one, the rebound stroke will be lower than the
analyzed stroke (as for the default option).
(B) If the Fixed Stroke, Variable Pressure Adjustment Option (Options,

General Options, Stroke) is selected for analyzed strokes less than
the “normal” one, a pressure reduction is applied until a stroke
convergence is achieved. If however the rebound stroke is lower
than the analyzed stroke, the single stroke option is used, i.e. no
upward adjustment of pressure is applied.

Earlier program versions did make an upward pressure adjustment
for diesel hammers if the pressure adjustment option was chosen.
However, the results for high strokes showed unrealistically high
transferred energies and therefore were potentially non-
conservative.
3.14.4 Diesel Analysis Procedure
A flow chart for diesel analysis is shown in Figure 3.14.1. Under all stroke
options, the program calculates the ram velocity at the exhaust ports based
on either the rated stroke or the user selected down stroke. Then the wave
equation analysis process begins with the diesel pressure calculation
performed for the three phases of the process: Compression, Combustion
and Expansion.
Immediately prior to the impact, the ram velocity is reduced according to the
hammer efficiency value. After impact, both due to ram rebound and diesel
pressure, the ram begins to move upwards. After the ram position has
reached the ports during the upwards ram motion, the program either
continues with the wave equation until the stop criteria are satisfied or
calculates the upward stroke from the upward ram velocity. The analysis
proceeds depending on the stroke option:
(a) Single analysis with fixed stroke and pressure: the wave equation
diesel analysis is finished after the program has calculated the
upstroke.
(b) Convergence of stroke with fixed pressure: this is the commonly

employed option under which the analysis is repeated with the
downstroke equal to the calculated upstroke until stroke convergence
has been achieved.
(c) Convergence of pressure with fixed stroke: the analysis is repeated

with the same down stroke and a Pmax value that is proportionally
adjusted to the difference between down stroke and up stroke. An
exception is the Inspector’s Chart option for which only pressure
reductions will be made.
For stroke options b and c, when the calculated upstroke exceeds the
maximum hammer stroke (or when the closed end diesel uplifts), the
analysis is repeated with a reduced ultimate pressure (fuel reduction) until
the upstroke is less than the maximum stroke. (Note that the maximum
stroke is sometimes greater than the rated stroke.)
The starting stroke automatically chosen by the program is equal to the

rated stroke of the hammer. This starting value may not be the best choice
when a low resistance is analyzed. Then the available energy may be so
large that the pile penetrates so much under the hammer blow and

practically no upwards stroke can be calculated. In this case the program
attempts a second analysis with a much lower stroke.
For hammers deemed large relative to the soil resistance, energy may still
be too high and the ram will not rebound. Then a “Hammer will not run”
message may generate and no output will be made for that capacity or
depth. The user may try other starting stroke values to overcome this
problem; however, a better remedy would be the selection of a smaller
hammer.
Figure 3.14.1: Diesel analysis flow chart
3.14.5 Vibratory Analysis Procedure
The computational procedure is very similar to that for impact hammers. All
three analysis options can be performed with frequency taking the place of
stroke as the independent variable. Also, instead of blow count, the time
required for unit pile penetration is calculated (seconds per foot or per
meter).

 The analysis is begun by calculating the vibratory force which, as
long as it is directed downward, compresses the pile top spring
and extends the spring connecting the two vibratory hammer
masses.
 The vibratory force is subject to three potential reductions: start-up

time reduced frequency, user specified "efficiency", and engine
power limit. The latter is applied when the power per cycle
exceeds the power rating of the hammer.
 From cycle to cycle the program monitors the pile top penetration
time. Once the penetration time has converged, or after the
maximum analysis time has been exceeded, the analysis is
finished and the program proceeds with analyzing the next
capacity value, depth value, or frequency depending on the
analysis option.

4. INPUT INFORMATION
The range of the required input data varies strongly, depending on the
complexity of the problem to be solved. For example, the input for a simple
bearing graph analysis can be entered on the Main Input Screen while a
driveability with static analysis of a non-uniform, spliced pile may require
data in at least 6 different screens. However, it has been attempted to make
the input procedure as simple as possible. For this reason, the program
calculates pile model details like springs and masses and distributes the
shaft resistance to the various pile segments. For further simplification of
the input preparation, the program database includes the models of
hammer and driving systems. However, very basic soil and pile information
must be supplied by the user.
Prior to data input, pertinent information should be collected with the aid of
Form 1, reproduced below, which was taken from Hannigan et al. (2006).
This form can be downloaded from PDI’s website:
http://www.pile.com/Specifications/Sample/histrain.rtf.
For the beginner it is strongly recommended to perform the example

problems. Then after they have been understood, the input process should
be begun by clicking on the “New Document” icon. The analyst will then be
guided through the necessary input sections.
4.1 Hammer Data
The hammer manufacturer name and model No. is usually sufficient, since
the hammer data file contains all necessary information for commonly used
hammers. Further help files are available during program execution by
clicking on Help or by pressing function key F3 after placing the cursor on
the data field for which help is needed.
For hammers whose data have not been entered into the file, hammer data
should be requested from the manufacturer using Form 1. The necessary
information depends upon the hammer type. If the hammer manufacturer is
not familiar with the data required by GRLWEAP, PDI should be contacted
for further help. For estimated efficiency values, refer to Section 3.3.8. For
battered piles, additional efficiency reductions should be made as explained
earlier and in the Help section.
4.2 Driving System Data
The driving system input data, consisting of the hammer cushion properties,
helmet weight (including striker plate, inserts, adapters, etc.), and pile
cushion properties (in the case of concrete piles). All of this data can be
entered in the Main Input Screen. Only if the actual field data is not known
should the help file data of GRLWEAP be used. The GRLWEAP stored
data can be retrieved using the F3 function key while the cursor is placed
on a driving system data entry field.

Cushions can be specified either by their area, elastic modulus, and
thickness or by their stiffness. The stiffness value will override the other
three inputs. In addition, a coefficient of restitution must be entered as
specified by the material’s manufacturer. The round-out deformation is
usually left unchanged at its default value (0.01 ft or 3 mm).
Helmet weight is the weight of all components between hammer and pile
top. The GRLWEAP supplied data may not include the weight of all of these
components.
Pile cushion area is usually equal to the pile top area, and the program
would take that as a default. It would also defaults to an elastic modulus for
relatively new plywood. Only the thickness of the cushion needs to be
entered. The user should be aware, however, that softwood cushions
generally compress during pile driving. A study described by Rausche et al.
(2004) suggests that the elastic modulus of plywood for end-of-driving
analyses should be chosen roughly 2.5 times higher than for early driving
situations with new plywood (75 ksi instead of 30 ksi or 500 MPa instead of
200 MPa). The 2.5 times increase of modulus automatically accounts for
reduced thickness effects and therefore can be used in conjunction with the
nominal cushion thickness.
4.3 Pile Data
Required pile data consists of total length, cross sectional area, elastic
modulus, and specific weight, all as a function of depth. This is the so-
called pile profile. For non-uniform piles, these values must be entered as a
function of depth in the P1 input form. An alternative input form allows for
the entry of a number of uniform segments (in the non-uniform pile window,
the section input icon is active). The offshore version also offers an optional
input mode which considers add-ons with cut-off and stabbing guides.
For Two-pile analyses, the second pile profile, whether uniform or not, must
be input in P2. This may only be occasionally necessary, if two piles are
driven in parallel. This type of analysis is possible; however, it is complex
and potentially inaccurate. If both piles are under the same cap and have
the same length and resistance distribution, they could be considered as a
single pile with a cross sectional areas equal to the sum of the two pile
areas. Also, if one pile was driven with its toe against the top of a second
pile, again a single, nonuniform pile analysis would be more reasonable and
accurate than the Two-pile analysis. (The analysis of a follower on top of a
pile is a typical example for a non-uniform single-pile analysis.)

A Two Pile Toe analysis is recommended when a pile has a size reduction
along its length, which causes soil displacement and, therefore, a second
pile toe effect. The total end bearing can be distributed between the two
pile toes and damping and quake can be specified for both.
A Pile Splice analysis must be performed if the pile, somewhere along its
length, allows for extension with zero tension force. The distance of force-
less extension is called a “slack”. This occurs, for example, when a pile is
mechanically spliced. Obviously, the follower on top of a pile has an
unlimited extension at its bottom and therefore a practically unlimited
tension slack. This situation is also modeled with a splice input which has a
large slack. A crack in a pile exhibits a reduced compression force while the
crack closes under compression. This would again be modeled with a
splice, where the tension slack could be made very small (but it must exist)
and the compressive slack is modeled by the round-out input. To enter a
splice click on Options/ Pile Parameters/ Splices; then enter the number of
pile splices to be modeled, click “Update” and then enter the depth, tension
slack, compression slack and coefficient of restitution data. Note: if a very
soft material with low coefficient of restitution (like a softwood
cushion) is modeled between two stiffer elements, then it is important
that the segment with the low stiffness also has the low coefficient of
restitution or the energy losses will be incorrectly calculated in the
analysis. For that reason (and really under all circumstances), the
Numerical Output, showing the pile model, must be very carefully
reviewed and corrections to the input made if necessary.
Input pile properties also include the Critical Index which is either 0 or 1.
This input is only useful for the analysis of a pile consisting of more than
one pile material. The sections which are marked as critical will be the ones
checked for maximum stresses (see also output description).
The pile perimeter is needed for converting unit shaft resistance to total
shaft resistance. As mentioned earlier (Section 3.13.6) the perimeter is
easily assessed for a solid pile; however, for H-piles and pipes sometimes
questions exist. For H-piles, one usually chooses the box surrounding the
pile cross section. For open ended piles, over a certain distance the
perimeter may be increased or even doubled to consider friction over the
inside of the pile. However, no clear guidelines or correlations can be
referenced for this situation.
For a static analysis, the pile’s effective Toe Area must also be entered (on
the Main Input Screen and since 2010 in the S1 Screen). The Toe Area is
closely related to the soil resistance; this input allow the user for certain soil
layers to model the plugged, unplugged or partially plugged situation by,
respectively, entering steel annulus area, pipe gross area or a value in
between. As discussed in Section 3.13.6, this question is even more difficult
to answer than the perimeter question for open profiles. In general, it may
be assumed that H-piles plug during driving, and therefore the fully plugged
area may be used. For pipe piles, plugging depends on pile diameter, soil
density and depth of penetration into the dense material. Probably for

diameters of 20 inches (500 mm) or less plugging occurs in competent
soils. For pipes with diameters greater than 30 inches (900 mm) plugging
during driving is usually not expected. Under all circumstances, plugging
depends on the soil type, soil strength and penetration into the competent
soil layer. As mentioned earlier it is recommended to analyze both the
plugged and the unplugged situations to establish upper and lower bound
results.
Since 2010 a more realistic driveability analysis is possible, because the

end bearing can now be calculated with variable Toe Area values vs. depth
(in the S1 Screen). For example, if a soft clay layer is underlain by a very
dense sand, and if it is expected that the pile “cores” in the clay but plugs in
the sand, then the Toe Area should be, respectively in the clay and sand
layers, the pile toe steel cross sectional area and the total plugged toe area.
4.4 Soil
Static soil resistance calculations may be required before GRLWEAP

analyses. For bearing graph analyses, when wave equation results are to
be used in conjunction with an observed blow count, the soil resistance
calculations can be done in a more casual manner than for a driveability
analysis. The ST analysis, based on an assessment of soil density or
consistency, may be sufficient for a bearing graph analysis where only a
relative shaft resistance distribution and the percentage of shaft resistance
are needed as an input.
In a bearing graph analysis, it is common practice to allow the pile's depth

of penetration and (relative) soil resistance distribution to remain constant
throughout a series of analyses, even though the pile's ultimate capacity is
made to vary. In other words, it is usually unnecessary to recompute the
skin friction distribution, end bearing, quake, and damping for each ultimate
capacity. Instead one uses the soil resistance distribution that has been
calculated based on the soil investigation. The resulting resistance
distribution is really associated with long term pile resistance and strictly
applicable only to a redrive situation. The loss of resistance during driving
adds another inaccuracy to the approach if it is not properly accounted for
by means of setup factors.
When it is desired to calculate the blow count and stresses more accurately
for various depth values as the pile penetrates into the ground, the
driveability analysis must be chosen. In this case, the static soil resistance
should be input as accurately as possible. Static soil analysis provided by
GRLWEAP is based on a general soil type information (ST), SPT N–values
(SA), Cone Penetrometer values (CPT) and sand density and clay
undrained shear strength (API). Hopefully, the more detailed and accurate
the input is, the more realistic the results that can be expected. But as
mentioned earlier, static geotechnical analyses are inherently inaccurate
and should be complemented by local experience and dynamic testing. It is
the users responsibility to make all necessary corrections in the S1 screen
necessitated by the limitations of GRLWEAP’s static geotechnical analyses.

Although the pile can be specified as “Nonuniform” as far as its cross
sectional properties and perimeter, are concerned, special pile features like
a taper may require additional consideration for the different unit resistance
expected. Also second toes cannot be handled by GRLWEAP’s soil
analyses and must be handled by separate user calculations and input.
While, shaft quakes and toe damping are usually left constant with depth,
the toe quake generally varies with the type of pile and the density of the
soil and therefore with depth. Also the shaft damping values must usually
be varied for the different soil layers. The soil analyses routines help in that
regard, but the user is urged to carefully review what is automatically
generated.
4.5 Options
A variety of input, output, and analysis options are available in GRLWEAP.

Depending on the purpose of the analysis, these options might be
extremely helpful. In the program, most of these options can be accessed
through the toolbars, the icons, or the menu bar. Also, extensive help files
were built into the program that describe the options and explain their use.
The following are some of the major options available to the user.
Hammer options (automatically invoked by choosing the associated

hammer)
• Open end diesels
• Closed ended diesels
• External combustion hammers, i.e. air, steam, hydraulic or drop
hammers
• Vibratory hammers
Hammer parameter options (Options/ Hammer Parameters – except

Hammer Weight)
• Modification of Stroke
• Efficiency
• Combustion Pressure (diesels)
• Reaction Weight (closed end diesels)
• Combustion Delay to model pre-ignition (liquid injection diesels)
• Ignition Volume (atomized fuel diesels)
• Gas Expansion Coefficient
• Vibratory Frequency (vibratory hammers)
• Vibratory Delay (vibratory hammers)
• Line Force (vibratory hammers)
• Assembly Weight (external combustion hammers)
• Hammer Weight (options/ General Options/ Numeric)
Hammer file options

• Modification of a model in the hammer data file (View/ Edit Hammer
Database or double click on an ID number in the hammer window of
the main screen)

• User supplied new hammer model (View/ Edit Hammer Database)
Stroke options for diesel hammers (see Options/ General Options/ Stroke)
• Convergence of (or iteration on) stroke with fixed combustion
pressure; this is the normal mode of analysis.
• Convergence of (or iteration on) combustion pressure with fixed
stroke; this option is used when the stroke is known (say from
observation on site) but the associated pressure is uncertain. Note:
Allowing for a significantly increased pressure to match an unusually
high stroke can lead to non-conservative capacity results. In
Inspector’s Chart analysis option, the pressure is not increased
above the file specified pressure for conservative considerations.
• Single analysis with fixed stroke and pressure; this option is ideal
when analyzing a high stroke on a low soil resistance as it may occur
when the pile suddenly breaks through a hard layer
Driving system options

• With helmet (cap) by entering a number greater than zero
• Without helmet (cap) by entering a zero helmet weight
• With hammer cushion by entering either area, elastic modulus and
hickness, or a stiffness value
• Without hammer cushion by leaving at least stiffness and thickness
at zero
• With pile cushion by entering at least a nonzero thickness or a
stiffness (concrete piles only)
• Without pile cushion by leaving stiffness and thickness at zero
Analysis options (analysis option drop down menu in tool bar)

• Bearing graph, proportional is the standard result where shaft
resistance and end bearing are equally uncertain
• Bearing graph, constant shaft resistance; applicable when shaft
resistance is fairly well known and, for example, driving a short
distance into a bearing layer is modeled.
• Bearing graph, constant end bearing; applicable for situations when
end bearing is well known or insignificant.
• Inspector’s Chart; calculates the required blow count and associated
stress maxima for a single ultimate capacity value.
• Driveability; calculates blow count and stresses vs depth based on
user supplied shaft resistance and end bearing vs depth data
Driveability options
• Gain/loss factor for both shaft resistance and end bearing
increase/reduction to SRD (static resistance to driving); requires
appropriate soil setup factors in the soil resistance vs depth input (S1
Window)
• Variable setup for driving interruptions specified as “Waiting Time” in
the D Window; requires also input of relative energy and setup time
in the soil resistance input (S1 Window)
• Variable pile length; specify length for each depth to be analyzed in
the D Window

• Hammer, driving system modifiers; including fuel setting, efficiency,
cushion COR, and cushion stiffness input (D Window)
Static geotechnical analysis options

• Static analyses; accessible from Main Input Form (S1) and from the
S1 soil resistance window (ST, SA, CPT, API)
Pile options
• Variable pile weight (by specifying gravitational acceleration,
Options/ General options/ Numeric)
• Non-uniform piles (specify through the pile drop down menu)
• Single pile with two pile toes; not for driveability or RSA analysis
• Two-piles in parallel; not for driveability or RSA analysis
• Splices and slacks (specify in Options/ Pile parameters)
Pile input options (Options/ Pile Parameters/ Pile Segment Option)

• Automatic number of segments and segment properties (standard)
The following are not for driveability analyses
• Input of number of segments with automatic segment properties
• Input of number of segments and relative segment length with auto
segment stiffnesses and masses
• Input of number of segments, relative segment length, and segment
stiffnesses and masses
Splice input (Pile Parameters/ Splices)

• Splice modeling with slacks and coefficient of restitution
• Slack representation
• Crack representation
Soil shaft resistance distribution options (automatically generated for each

segment)
• Simple distribution on main screen; not for driveability analysis
• Variable distribution for situations that require more than a triangular
or trapezoidal distribution
Soil segment input options

• Automatic soil damping, quakes, and ultimate resistance values
• Input of segment soil damping with automatic quakes and ultimate
resistance values (Options/ Soil Parameters/ Soil Segment
Damping/Quake); not for driveability analysis
• Input of segment soil damping, quakes and ultimate resistance
values; (first choose “Detailed Resistance Distribution” in distribution
Drop Down Menu and enter for each segment the ultimate resistance
values; then click General Options/ Soil Parameters / Soil Segment
Damping/Quake); not for driveability analysis
Damping options (Options/ General options/ Damping)

• Case soil damping; only in conjunction with measurements
• Smith soil damping; recommended for all but RSA and vibratory
hammer analyses

• Smith viscous soil damping; recommended for RSA and vibratory
hammer analyses
• Gibson (Coyle) soil exponential damping; for research only
• Rausche exponential soil damping; for research only
• Hammer damping variation; for research only
• Pile damping variation; for research only
Numerical analysis options (Options/ General options/ Numeric)

• Residual Stress Analysis, which is applicable to flexible piles with
significant shaft resistance. It is recommended to always try this
analysis in addition to the standard analysis as it provides for more
realistic stresses and blow counts. For tapered pipe piles (e.g.
Monotube), RSA is always recommended. An entry of “1" is
recommended as it allows the program to perform up to 100 trial
analyses to reach convergence. Other choices would numbers
between 1 and 100 which would set the maximum number of trial
analyses allowed.
• Gravitational acceleration values may need adjustment if battered
piling or underwater pile driving is analyzed. In the former case,
adjustments must be made to include only the axial pile and hammer
weight components, in the latter case to consider the buoyancy of
the pile and hammer weight. For example, if a concrete pile is
subject to buoyancy then its effective weight is roughly 60% of its
weight above water. In that case, reducing the pile gravitational
acceleration to 6 m/s2 (19 ft/s2) would reduce the static weight
component of the pile. It would not reduce its mass.
• A larger “Phi” value (Time increment ratio) for the reduction of the
computational time increment; may be necessary when the analysis
becomes unstable (erratic results, non-proportionality between force
and velocity, and other “noisy” calculated pile variables vs time are
clear indications of instability; see variable vs time output). A number
300 would reduce the time increment by a factor 3 while default is
160 (1.6 reduction).
• An increased number of predictor-corrector iterations beyond the
default of 1 is not recommended.
• The maximum analysis time occasionally may need to be increased
if there is evidence that either blow counts or stresses have not
peaked within the analyzed time period. Examples where this may
be needed are analyses with very low resistance or vibratory
hammer analyses with low frequencies. Experimenting with this
number may help determine if this is a necessary adjustment.
• Hammer Cushion round-out values are usually not modified although
for steel on steel impacts a reduction to 1 mm may be reasonable. In
order to better match measured records, Pile Cushion round-out
values sometimes are increased to significantly higher values than
the 3 mm (0.01 ft) default.
Output options (Options/ General Options/ Output)

• Normal numerical output includes extrema tables; see the numerical
output files; it is important that this listing is carefully reviewed prior

to accepting the results.
• Minimum numerical output is automatically chosen for the driveability
analysis to reduce the amount of output. It does not include extrema
tables. However, particularly for complex situations, including multi-
material piles, it is strongly recommended to also check the
Numerical Output (*.GWO file) for an indication of the location of
maximum pile stresses along the pile and the various maxima in the
different materials.
• Debug numerical output; only useful for those familiar with the
program code. This option may generate extremely large files when
driveability analyses are perfomed.
• Bearing graph plot - single result; standard output.
• Bearing graph plot - two results; convenient when bearing graphs
from two different cases are to be compared. (Read Second File in
the File Menu).
• Driveability (vs depth) plot - result from current gain/loss factor or
from more two gain/loss factors (View/ Ranges/ Selections).
• Variable vs Time plots; helpful to check stability of analysis, for
comparison with measurements and to learn about wave
propagation. Only last analysis of driveability analysis is accessible
when in Normal Output mode. Select quantities in Options/ General
Options/ Output:
- Mixed quantities (vs time) plot
- Acceleration (vs time) plot
- Velocities (vs time) plot
- Displacement (vs time) plot
- Forces (vs time) plot
- Stresses (vs time) plot
• Output segment numbers of the output variables can be chosen in
Options/ General Options/ Output
• Output time increment is the time interval at which individual
quantities are saved for output. For increased resolution in the
variable vs. time plot, choose a smaller value; for increased plot
length, choose a larger value (Options/ General Options/ Output).
• Output of frequency of stress maxima and stress ranges (Output in
the Offhore Wave Option: Driveability/ Edit/ Copy Stress Extrema or
Copy Blows vs. Stress Ranges.

5. OUTPUT AND HELP INFORMATION
5.1 Numerical Output
GRLWEAP produces output in a variety of forms, depending on the

analysis and output options chosen. It is important that the user checks
thoroughly the Numerical Output (*.GWO files). It contains:
• a listing of the input data file which may be permanently saved and
recalled.
• the hammer and pile model with soil resistance parameters.
• extrema tables (not for output option: “minimum output”) with maxima
of force and stress each (both tension and compression), velocity,
displacement, and transferred energy, for every pile segment and for
every capacity value analyzed.
• a summary of the results in the form of blow counts, stress maxima,

stroke, and transferred energy for each capacity value analyzed. For
multi-material piles see note below.
• for the driveability analysis, the “vs depth” tables, i.e. major results
listed for each gain/loss factor as a function of depth.
• for diesel hammers, the strokes analyzed and the associated

combustion pressure
The numerical output listing also includes certain warning messages or

program performance indicators. For example, non-convergence of
residual stresses may have occurred or an excessive diesel hammer stroke
may have been calculated, and the program would warn of this condition
(although it would adjust the combustion pressure automatically to account
for that condition). Thus, review of the numerical output file is an absolute
necessity.
For the driveability analysis, the numerical output can be very long,
particularly if many depths are analyzed with several gain/loss factors. For
that reason, the default numerical output option is automatically set to
“minimum” and extrema tables are subsequently not shown. It may
therefore be advantageous to select the “normal” output option, even
though the output may then get long. Note that for each analysis depth, the
pile and/or soil model may be quite different, and therefore, careful
checking is essential. Also, the end of the numerical output listing for
driveability analysis includes a summary of the user-submitted soil
resistance parameters. Since these parameters are subject to modification
by set-up or driving induced capacity reduction, careful checking is
advisable.

5.2 Bearing Graph
The second type of output is the Bearing Graph, both numerically and
graphically displayed. This type of output is available for the Bearing Graph
and the Inspector’s Chart analyses. A variety of scale options exists in
View/ Ranges/ Selections.
The bearing graph output can also be done for two analyses in the same
plot. After displaying the bearing graph from the first analysis result, click on
nd
File/ Read 2 file and then browse to find the bearing graph data that you
want to add to the first output.
This output option also displays the numerical summary table. Both
graphical and numerical data can be copied and pasted into other
applications such as a word processor. Click on the graph or table and the
on Edit/ Copy to clipboard and then proceed with the pasting in the other
application.
5.3 Driveability
After a driveability analysis has been performed, instead of “Bearing Graph”

a “Driveability” option will be available, It provides for numerical and
graphical summaries for up to two Gain/Loss factors (View/ Ranges and
Selections). Scales can be changed in the same window (choose the Graph
Tabs) and copy/paste options are as for the Bearing Graph.
5.4 Variables vs. Time
Additionally, Variables vs Time can be plotted or listed. The variables

include accelerations, velocities, displacements, forces and stresses, for
every pile segment. In order to reduce disk space requirements, this output
is only available for a reduced set of piles segments (as selected in
Options/ General Options/ Output), and for driveability analyses only for the
last analysis. Pile force and velocity can also be displayed at a proportional
scale for both the top segment and one additional user selectable segment.
Numerically, variables vs time can be transferred to other programs using
the copy and paste features of the windows system. The output time
increment (Options/ General Options/ Output, Edit Segment Numbers)
sometimes must be made longer, e.g., 1 ms, to allow for plotting of the
whole range of calculated time period in the variable vs time plots. This may
be of particular interest when the analysis time has been increased or the
length of pile segments (and because of the shorter critical time also the
time increment) has been decreased. In addition to proportional force
velocity output for the pile top, another segment can also be designated for
force and proportional velocity output in Options, General Options, Output,
Edit Segment Numbers. This is only meaningful for the Mixed Variables.
Note that the pile variables can also be displayed in the 3-D plot.
Note about maximum stress results: The stress maxima are normally the
numerically highest values occurring somewhere along the length of the
pile. This is satisfactory for piles consisting of only one type of material.

However, for multi-material piles, the critical stresses are of greater interest
and should be included in the summary table. For example, in a concrete
pile with steel tip, the stresses are numerically much higher in the steel than
in the concrete, yet we are really interested in the maximum tension
stresses in the concrete. For that reason, the Critical Index input has been
provided in the P1 input form, which selects for the summary table only
stress maxima which occur in the critical sections. However, in order to
avoid missing potentially damaging stresses in sections which were not
considered critical, the analyst should not trust these automatically selected
values exclusively and additionally look at the extrema tables of the
numerical output. These tables will also tell when and where these critical
stresses occur along the pile.
5.5 Stress Maxima Range Ouput for Fatigue Studies
This is an Offshore Wave option
Fatigue studies are done in different ways, sometimes requiring the number
of stress maxima and sometimes the number of certain stress ranges
occurring during pile installation. Selecting that information from extrema
tables and finding the associated number of blows for each pile segment is
very time consuming at best. To simplify this process, GRLWEAP has
added two types of summary tables one for stress maxima and one for
stress extrema. These tables can be transferred to a spread sheet.
GRLWEAP does not provide tools to display or otherwise manipulate them.
After performing a driveability analysis, GRLWEAP has saved the two files
containing stress information. The contents of these two files can be copied
in the Output Section of the program by clicking on Driveability and then
Edit. Two options will be displayed:
Copy Stress Extrema Data

and
Copy Blows vs. Stress Ranges.
Tables 5.5.1 and 5.5.2 show small portions of the stress extrema and stress
range tables, respectively. Both tables include listings for the gain/loss
factors chosen under View/ ranges and Selections. The extrema data
include pairs of columns for maximum compressive and tensile stresses for
every depth analyzed. It also shows the number of blows needed to drive to
that depth from the previous depth. The columns then list for each segment
the maximum stress calculated for that depth calculation.

Table 5.5.1: Summary Table of Stress Extrema
Stress Extrema for Gain/Loss 1 at Shaft and Toe 0.833 / 1.000
Depth (m) 1.83 3.66 5.49
Blows 0 4 8
Pile mxCstrss mxTstrss mxCstrss mxTstrss mxCstrss
Seg # MPa MPa MPa MPa MPa
1 0.1 0 149.6 0 156.7
2 0.2 0 150.1 0 157.3
3 0.5 0 150.5 0 157.8
4 1 0 151.1 0 158.5
Table 5.5.2: Summary Table of Stress Ranges

Blows vs. Stress Range for Gain/Loss 1 at Shaft and Toe 0.833 / 1.000
Stress Range 0 42 84 126 168

(MPa) 42 84 126 168 210
Seg #
1 0 0 0 22 93
2 0 0 0 22 93
3 0 0 0 22 93
25 0 0 0 10 105
26 0 0 0 18 97
27 0 0 0 32 84
28 0 0 0 115 0
Table 5.5.2 basically lists number of blows for select stress ranges (in 42
MPa increments in the example). The user has the option to refine the
stress ranges by choosing for example 10 instead of the 5 ranges shown.
Table 5.5.2 indicates that segment 28 was exposed to 115 blows with a
stress range (maximum – minimum compressive stress) between 126 and
168 MPa.
5.6 Help
Further information on available output options is available in the program’s

Help section which can be accessed by pressing function key F1 at any
point in the data input. This type of Help is given in written form describing

input parameters, option functions, and examples. For the novice, it may be
worthwhile to print out these articles for convenient reference. The
examples are also helpful as a demonstration of program capabilities.
Another form of Help is for direct data entry. For example, if the cursor is
activated on an input field that requires an area input, pressing function key
F3 will activate the “Area Calculator”. Other direct input helps are available
for driving system parameters and/or general cushion properties and pile
material properties. Finally, an easy way to get started with the input
process is the Data Entry Wizard which is invoked after pressing the New
Document icon (or New in File).

6. CONCLUSIONS AND RECOMMENDATIONS
GRLWEAP is a wave equation program for the analysis of the pile driving
process. It is based on Smith's original algorithm but offers a variety of
enhancements and options. The program analyzes what happens under the
dynamic load applied by either a ram impact or a vibratory hammer. The
program is not intended to predict the bearing capacity of a pile at a certain
depth from static geotechnical analysis. Instead, the four static analyses
available are thought to provide an aid in performing the dynamic analysis.
Basically, the program either predicts:
• the bearing capacity of a pile based on an observed blow count or
• the blow count based on a calculated or estimated static and dynamic

soil resistance.
A wave equation analysis can be run only if information about hammer,

driving system, pile, and soil is either known or assumed. It can then
calculate the motions and thus the penetration of the pile and its stresses
due to a hammer blow. The more accurate the input, the more realistic the
results.
Regarding hammer data input, it is most complex for diesel hammers

whose thermodynamic behavior is simulated in GRLWEAP. External
combustion hammers powered by hydraulic pressure, compressed air,
steam or cable are more simply represented. GRLWEAP also models,
vibratory hammers in a relatively simple manner.
The driving system is represented with bilinear springs and some non-
linearity (round-out). In this way, good agreement between measured and
computed pile quantities is often achieved.
The pile model considers the pile mass (segment masses), its elasticity
(springs), its structural damping (dashpots), and any slacks from splices. A
wide variety of pile systems exists, including those consisting of more than
one material or driven by a mandrel. Most commonly employed systems
can be fairly realistically represented and analyzed by GRLWEAP.
However, since the pile model is strictly linear and one-dimensional and
only axial motions, stresses and forces are calculated (see below) and any
yielding is not considered. On the other hand, residual stresses in pile and
soil can be estimated by performing repetitive (blow after blow) analyses. In
general, RSA leads to greater calculated pile sets per blow and higher
stresses than the standard Smith analysis which assumes that the pile
stresses are zero prior to hammer impact.
The dynamic soil model considers the soil's elasticity (quakes), strength
(capacity), and dynamic behavior (damping factors). There are a number of
extensions to the soil model for damping (viscous, exponential), plug

representation, soil radiation damping (soil motion), etc. However, these
extensions are experimental and only of interest to the researcher.
The user of the wave equation approach should realize that the dynamic
analysis represents the soil in its disturbed state. Estimates of soil setup or
relaxation must be additionally considered. For example, if a pile is driven
and its blow count is observed at the end of driving, the wave equation
bearing graph will provide an estimate of the bearing capacity at the end of
driving based on that blow count. Soil setup is likely to add additional soil
strength along the pile shaft, while relaxation effects might reduce the end
bearing. One day, one week, or one month later, the pile may have a
capacity that differs significantly from the end of driving value. The user
must estimate these effects, or better, perform restrike or static load tests
for a more accurate capacity assessment.
Output is provided by the program in both numerical and graphical form.

Most importantly, the program calculates for a given bearing capacity value
both blow count and stress extrema. Capacity or stress vs blow count
establishes a bearing graph. Listing or plotting the results as a function of
depth result in the driveability result. For comparison with dynamic
measurements conducted during pile driving, forces and/or motions may be
plotted as a function of time.
The GRLWEAP wave equation model is obviously a great simplification of

the real world and certain unusual circumstances may only be crudely
represented. Furthermore, the model parameters are often inaccurate. For
example, they may not represent the hammer’s actual state of
maintenance, the soil’s in-situ static and dynamic behavior, or situations like
plugging. For high blow counts, when the pile motions are small,
incomplete resistance activation may occur and non-linear soil resistance
effects or radiation damping may introduce greater errors than for easier
driving conditions. On the other hand, very easy driving conditions with
permanent sets in excess of 15 or 20 mm may also produce uncertainty
due to high dynamic soil resistance components. Thus, where experience
lacks, measurements, both static and dynamic, are the only way to assure
an accurate assessment of bearing capacity. It is for that reason that
modern safety factor concepts distinguish between different methods of
capacity determination. For wave equation analyses, the typical overall
factor of safety is between 2.5 and 2.8.
As mentioned above, the GRLWEAP provides a one-dimensional analysis.

Thus, stresses caused by bending, non-uniformities of soil resistance or
non-symmetric pile shapes are not calculated. For the stress results, it is
therefore important to realize that the calculated values are averaged over
the cross section and can be easily exceeded if the hammer-pile alignment
is poor, the pile experiences bending, or the toe resistance is subjected to a
non-uniform rock surface.

APPENDIX A: CORRELATIONS
For traditional wave equation work, the most important correlation is that of
capacity based on observed blow count. A very early study was published
by Blendy (1979). A comprehensive correlation study has also been
reported by Thendean et al. (1996). It shows that the correlations between
predicted and measured bearing capacities are dependent on time effects;
restrike tests and corresponding static load tests should therefore be
performed at comparable waiting times after time of pile installation. The
study also shows that restrike test results produce greater scatter than end-
of drive results. This can be explained by the uncertainty of blow count and
energy in restrike situations: the set per blow changes from blow to blow
while hammer performance generally improves. Also during a restrike, the
capacity of the pile often changes as the pile loses setup soil resistance or
regains relaxed toe resistance.
A comprehensive study on the prediction of blow counts based on wave

equation and soil resistance calculated from static geotechnical analyses
has not been made. Because of the difficulty of predicting soil resistance
accurately from soil borings, there is much more volatility in these results
than in capacity predictions which are based on observed blow count.
A more recent study on stress, diesel hammer stroke, and transferred

energy was published by Rausche et al. (2004) showing that the greatest
uncertainty is introduced by the relatively soft pile cushion when driving
concrete piles. In fact, the study suggests that for end of driving situations,
used cushion properties should be used. For example, plywood cushions
should be analyzed with 66% of nominal thickness and with an elastic
modulus roughly 50% higher than the normally recommended value (300
instead of 211 MPa or 43 instead of 30 ksi). Early driving situations can be
analyzed with the nominal thickness and a modulus corresponding to a
slightly used material.
Anecdotal evidence suggests that GRLWEAP predicts lower than actual

diesel hammer strokes. Indeed, GRLWEAP occasionally underpredicts
strokes; however, there is no real evidence that stress or energy results
have a bias. Hammers vary in their performance characteristics not only
after months of use and abuse but even during a day depending on ambient
temperature or weather conditions, the amount and hardness of pile driving,
and other factors. Therefore, differences between energy and stress
results from analysis and measurements must be expected to be in the 10
to 20% range. Further information on GRLWEAP’s performance can be
found in Rausche et al., 2004. That reference also suggests that diesel
hammer stroke results are somewhat underpredicted (3% on the average)
and because of this potential underprediction it is suggested that stroke
results are used in the following manner:
Accept results if the observed stroke is within 0.9 and 1.2 times the
calculated value. If stroke is severely underpredicted, repeat analysis only
with higher combustion pressures if (a) the actual stroke exceeds the

calculated value by more than 20% and (b) it is assured that the high stroke
is the result of good hammer performance and not preignition. It is
suggested to adjust the pressure only so far that the calculated stroke is still
about 10% lower than measured. To adjust stroke by 10%, increase the
maximum combustion pressure by 10%. If stroke is more than 10%
overpredicted, it may appear that the hammer is not in working order.
Reduce the maximum combustion pressure to make the computed stroke
match the observed one.
It is always recommended to make conservative predictions; conservative

predictions has different meanings for different tasks as follows:
 For capacity from blow count, use a pessimistic hammer

performance value (lower efficiency).
 For stress predictions during driving, use an optimistic hammer

performance (higher efficiency).
 For blow counts in a driveability analysis, make an optimistic high

soil resistance assessment and a pessimistic hammer
performance assumption.
 For stresses in a driveability analysis for steel piles, make an

optimistic (high) soil resistance assessment and an optimistic
hammer performance assumption.
 For stresses in a driveability analysis for concrete piles, use two

different analyses, one with an optimistic (high) soil resistance
assessment and hammer performance assumption and the other
with a pessimistic (low) soil resistance assessment and an
optimistic hammer assumption (for high compression stresses and
high tension stresses, respectively).

APPENDIX B: HAMMER MODEL DETAILS
B1 Diesel Hammer Studies
Throughout the development of the various WEAP program versions and

the GRLWEAP software, emphasis has been placed on realistic hammer
models. The complexity of the diesel hammer, consisting of a variety of
different makes, requires comparative analyses to produce a realistic
mathematical representation. The Background report of the previous
GRLWEAP documentation summarized these studies and included
correlations of measured and computed results. Included in these
comparisons were quantities such as maximum pile top force, maximum
transferred energy (ENTHRU) and diesel hammer stroke. The 1986 study
and related hammer model improvements were based on 57 different test
results. For the 1998 and later GRLWEAP program versions, the original
hammer studies, although still relevant, were not reprinted in this report.
The diesel hammer model has undergone a variety of changes which were
made necessary, for example, by hammers that produced higher and
higher strokes. One of the necessary change involved the determination of
the maximum combustion pressure in a consistent manner for all diesel
hammers; another one concerned a modification in which the pressure –
volume relationship was calculated, requiring a different adiabatic
expansion coefficient. These changes helped calculate more reliably and
realistically strokes while at the same time producing calculated pile top
forces and transferred energy values that agreed reasonably well with
measurements.
B2 2002 Method for Diesel Hammer Pmax Calculation
The maximum combustion pressure, Pmax, is the most important parameter

in the diesel hammer model for diesel hammer stroke calculations. A large
Pmax value not only makes for a large hammer stroke, but also adds
substantial transferred energy (ENTHRU) even if the stroke is kept constant
in either a single stroke analysis or one that allows for stroke convergence
with fixed pressures. Analyses with fixed stroke and convergence of
pressure are, naturally not dependent on the P max value in the hammer data
file. Direct measurements of P max are complicated, expensive, and subject
to a variety of influences and errors. Most importantly, on a test stand,
hammer combustion pressures usually do not represent the typical working
conditions and are therefore not representative. A procedure was therefore
developed that produces a reasonable P max value based on the hammer’s
rated energy. Essentially, the procedure determines that pressure value
that would produce the rated stroke in a refusal condition on a pile that is
matched to the hammer size. A check is also made for a reasonable
transfer energy value in the theoretical test stand.
The “test stand” is assumed to be a steel pile driven into rock; the pile
properties are matched to the hammer size as follows:

Pile Length, Lpile (ft) = 50 ft + ¼ of rated energy of hammer in kip-ft
Lpile is limited up to 200 ft to consider larger hammer.

2
Pile Area, Apile (in ) is based on a pile weight to ram weight (W ram in kips)
ratio of 2.
Thus,
2 3
Apile (in ) = 2 x W ram(144) / [(0.492 kips/ft )(Lpile in feet)]
A driving system is also included with the following parameters:
Helmet weight (kips) = 20% of ram weight
Hammer cushion stiffness (kips/inch) = W ram/(0.0004 inches) = 2500 (W ram

in kips).
Hammer cushion coefficient of restitution = 0.8.
For the soil resistance the following parameters are set:
The automatic Rult values of the GRLWEAP Version 2002 program are
used in a standard bearing graph. However, the highest R ult value must
produce a blow count at or above 240 b/ft.
Default damping (0.2/0.15 s/ft) and quakes (0.1 inches).
Triangular resistance distribution with 10% shaft resistance.
Several bearing graph analyses are then performed. The P max value is
adjusted until the stroke at refusal is equal to 95% of rated stroke and until
the transferred energy is less than or equal to 50% of rated. The latter
corresponds to the 90% point in the rated energy histogram of GRL’s diesel
on steel pile data collection. In other words, only 10% of all diesel hammers
driving steel piles will transfer more than 50% of their rated energy at EOD
to a steel pile. In general the transferred energy calculated by GRLWEAP
is significantly less than 50% and more likely the mean value of 37% (see
table).
Note: The following method has been used to determine the maximum
combustion pressure for all open end diesel hammers, except for the ICE I-
series hammers. Correlation studies for this series of hammers showed
that hammer performance was better modeled by using 95% of the
hammer pressure used in GRLWEAP 1998 than by using the standard
algorithm.
B3 Measured Hammer Performance

GRL Engineers, Inc. (formerly Goble Rausche Likins and Associates, Inc.)
has taken measurements on many different construction sites and on many
different hammer-pile systems. For end-of-driving situations, these
measurements, pile top force and velocity, were used to calculate
transferred energy and from it, by division with the rated hammer energy,
the so-called transferred efficiency or transfer ratio. GRLWEAP calculates
the equivalent value named ENTHRU. These transferred efficiency values
were organized by hammer and pile type. A statistical evaluation was then
made and, in 2009 yielding the results of Table B1.
Table B1: Measured Transfer Efficiencies (Energy in Pile Divided by

Manufacturer’s Rated Energy (%)
Hammer Type Steel Piles Concrete and Timber

(GRLWEAP
Hammer No. Mean CoV No. Mean CoV
Efficiency) Cases % % Cases % %
All Diesel
1419 39 26 668 26 30
Hammers (0.8)
Single Acting
747 56 23 194 41 29
Air/Steam (0.67)
Double Acting
68 40 34 47 32 33
Air/Steam (0.50)
All Hydraulic
203 69 24 67 47 34
(0.80/0.95)
The All Diesel category includes both open end and closed ended diesel
hammers and both atomized and liquid injection type hammers. The
GRLWEAP standard efficiency is 80% while on steel piles the transfer
efficiency averages 39%. That means that the pre-compression phase, the
driving system and the impact event itself cause the difference loss of 41%.
Indeed it can be expected that the compression costs about 25 to 33% of
the rated energy and that leaves an estimated 8 to 16% of the losses to the
energy transmission process through the driving system. The concrete piles
receive only 26% of the rated energy; the 13% difference between the steel
piles and concrete and timber piles is the energy lost in the cushioning or
the wooden pile top. (The very top of a timber pile often brooms and,
therefore, behaves like a softwood cushion).
The second group of hammers are the traditional air pressure or steam
powered hammers whose upward and downward motions are controlled by
ram position. This can lead to problems like pre-admission which can self
cushion a hammer. These hammers also lose 13% due to driving system
and impact event and an additional 15% in the pile cushion on concrete
piles.

Double Acting Air/Steam hammers are either traditional double acting,
differential acting or compound hammers. They may be powered by
compressed air or steam. In hard driving, i.e., at the end of driving, these
hammers often have to be run at reduced pressure to avoid uplift. That
pressure reduction reduces their down ram acceleration and makes that
hammer type somewhat less efficient and more erratically behaving. It
appears that this hammer category loses 10% due to driving system and
impact event and additional 8% in the pile cushion.
The fourth category shown in the table includes measurement results from
a variety of modern hydraulic hammers. They are given many names such
as hydraulic free-fall hammers, hydraulic drop hammers, hydraulic-power
assisted hammers, doubling acting etc. These results also include those
from hammers with internal monitoring of the kinetic energy. Obviously,
these hammers are very different in design, rating, and relative
performance and that may explain why their COV (coefficient of variation) is
surprisingly high even though each individual hammer make performs with
much greater reliability than the other hammer types. However, not enough
data has been collected to make statistical summaries of the various
hammer makes meaningful. For the hydraulic hammers the difference
between steel and concrete performance is a surprisingly high 22%. This
may be explained by the rather high impact velocities of at least some of
these hammers which then requires relatively thick cushion stacks.
In summary, the statistical results suggest that concrete piles receive

between 8 and 22% less energy of the rated energy than the steel piles.
Estimated losses in the driving system and the impact event itself vary
between 8 and 16%.

APPENDIX C: GRLWEAP FIRST STEPS
Whether or not you are a seasoned wave equation analyst, GRLWEAP may
present challenges, and you may benefit by reading the following section
for basic help with the program's options and capabilities and hints for
solving a basic problem. In additon, however, you should refer to the „Help“
offered in on line while performing the program.
Starting the Program
Instructions for installation are provided separately as an insert with your

GRLWEAP Manual. With the proper installation accomplished, you may
start the program by clicking on the GRLWEAP icon or by selecting the
program GRLWEAP application using the Windows Explorer. Please be
aware that a license, i.e. a key, either a software key or hardware key, is
required for the program to run. If you have problems using the program,
please refer to GRLWEAP FAQ section on our website (www.pile.com), and
if you don’t find the solution there, contact the software department of Pile
Dynamics, Inc.
After starting the program, it is wise to check and set your desired unit
system (SI or English). The program will remember this unit system after it
has been set during subsequent program runs.
Before Executing the Program
Prior to doing actual calculations, you should be able to answer the

following questions:
• Why do I need this dynamic pile analysis and what results do I need?
• What are the basic parameters to be analyzed (Pile properties, hammer

and driving system, soil details, design load, ultimate capacity or
nominal resistance)?
• How will I assure that the results are realistic? What field testing will be
done. What factors of safety will be used?
• In what form do I want to present the results?
Answering these questions should provide the basic data needed for the
program input.
Data Input
It is strongly recommended to start each new data analysis by clicking on

the New icon or on New under File. While assuring that no hidden data
from previous program runs are present, New will guide the user through
title and file name entry and many (though not necessarily all) other
parameters needed for a basic analysis. These are the same data entries

that are described in the following section on the Main Input Form. After the
user has completed the data entry, GRLWEAP presents the data in the
Main Input Form.
The Main Input Form
The Main Input Form consists of tool bar (top), Data Entry Fields (left side)
and a graphic display area as a partial help for checking the data submitted
(right side). The various data entry fields accept inputs of:
• Job Information
• Hammer Information or data file ID, or direct hammer selection
• Pile material selection
• Cushion Information for hammer and pile, and helmet information
• Pile Information
• Ultimate Capacities or Resistance Gain/Loss Factors - Bearing
capacities to be analyzed in Bearing Graph or Inspector's Chart Options
or Gain/Loss Factors (to be applied to long term static resistance
values) for the Driveability Analysis
• Dynamic Soil Parameters - Averages for shaft damping and quake, toe
quake and damping for bearing graphs, and default damping and quake
values for driveability analyses
• Shaft Resistance percentage and resistance distribution parameter for
the simplest cases in a bearing graph
For a bearing graph analysis of a uniform pile with simple resistance

distribution, the Main Input Form generally suffices for data input. For more
involved situations, one or more additional Input Forms must be filled in.
They are accessible through the View menu or corresponding icons and
under menu entry Options. The Main Input Form displays most of the
selected options at appropriate locations. However, it does not allow for
direct modification of these options.
The user can choose major options from the following four option menus:
• The Unit Option, allowing for choice of SI or English units

• The Soil Resistance Distribution Option, to choose between simple
resistance distribution, variable resistance distribution, and detailed
resistance distribution input (segmental input)
• The Pile Option, to choose between uniform pile, non uniform pile and
two pile analyses
• The Analysis Option, to choose Bearing graph (assuming proportional
or constant shaft resistance or constant end bearing), or Inspector's
Chart or Driveability analyses
Drop Down Menus
View - Depending on the selections made for Pile, Soil, and Analysis
Options, the following Input Forms are accessible:

• Main Input Form
• Pile 1 Input Form, accepts input of cross-sectional properties if Pile 1 is
non-uniform, if 2 piles are analyzed in parallel, or if 2nd pile toe is to be
analyzed; access through View or P1 icon
 Accessible from the Pile 1 input form is the Pile Section Input
(click Options/ Pile Parameters/ Pile Profile Section Input); it
allows for somewhat simpler input than the Pile 1 input form, if
the pile consists of several uniform sections (not to be confused
with the input of individual segment parameters, stiffness and
weight).
nd
 Also the 2 Pile Toe can be accessed from the P1 Pile 1 input
form.
• Pile 2 Input Form, (to analyze 2 piles; serves for the input of the 2nd
pile’s profile and the connection between the piles (pile attachment));
access through View or P2 icon
• Resistance Distr., Pile 1 Input Form, for the bearing graph, if the
Simple Resistance Distr. is not sufficiently detailed and ST, SA, CPT or
API cannot be used; or for the Driveability Analysis; or for 2-Pile
Analyses; access through View/ Resistance Distr./ Pile 1 Input Form
or use S1 icon.
• Resistance Distr., Pile 2 Input Form, (always necessary for 2-pile

analysis); access through View/ Resistance Distr./ Pile 2 Input Form
or use S2 icon. Two-pile analysis has to be selected first in the Uniform
Pile Drop Down Menu.
• Depths, Modifiers Input Form, to select those depths at which a

driveability analysis is to be performed; click View/ Depths/ Modifiers
Input Form or use D icon. Driveability analysis must be selected first in
the analysis drop down menu initially at Bearing Graph.
• Soil Type Static Analysis Input Form, generally useful for calculating a
reasonable resistance distribution for bearing graph analyses or for
driveability analyses after choosing the Variable Resistance Distribution;
access through View or ST icon.
• SPT N-value based Static Analysis Input Form, may be used as a help
in preparation for bearing graph or driveability analyses; after choosing
driveability, access through View/ Static Analysis Input Form or SA
from the S1 input form.
• CPT (Cone Penetration) based Static Analysis Input Form, may be used
as a help in preparation for bearing graph or driveability analyses; after
choosing driveability, access through View/ CPT Input or CPTfrom the
S1 input form.
• API conforming Static Analysis Input Form, may be used as a help in

preparation for bearing graph or driveability analyses; after choosing
driveability, access through View/ API Static Analysis or API from the

S1 input form. For Offshore Wave Version only.
• Edit Hammer Database, to enter a new hammer or modify existing

hammer data; click View, Edit Hammer Database or double click on
any one of the hammer names shown. Once the hammer data base is
opened, double clicking on an individual data entry opens a hammer
data input form which then can be modified.
• Output after an analysis has been performed; starts output program;

accessible through View/ Output or click on OU.
• View Input File shows the numerical data contained in an input file
which can be saved and reanalyzed at any time; accessible through
View/ S1 input form.
Options - The following options can be accessed through the Options

menu.
• Check Status causes program to check whether or not input is
complete.
• Job information can be used to enter Problem Title and/or File name
and location.
• General Options, Damping tab
 Soil damping option (Options/ General Options/ Damping)
- Case damping (for research or when measured)
- Smith (default)
- Smith viscous (for Residual Stress Analysis)
- Coyle and Gibson (for research)
- Rausche (for research)
 Hammer damping option, normally used at default (Options,
General Options, Damping)
 Pile damping option, normally preset based on pile top material
selection (Options, General Options, Damping)
• General Options/ Output controls plotted output type and numerical
output quantity
 for Variable vs Time output, choose between
- Mixed (default)
- Aceleration
- Velocity
- Displacement
- Forces
- Stresses
 For all except the mixed quantities:
- Choose Output segments, pile segments for which forces, etc.
can later be plotted and numerically displayed.
- Output Time Interval, to cover longer output time intervals at the
expense of a better resolution.
 For the mixed quantities choose an additional FV Segment for which
force and velocity will be saved for later plotting at a proportional
scale.
 For the Numerical Output, choose between

- Minimum, preferred and default for long driveability analyses
- Normal,preferred for input and result check, for all except long
driveability analyses
- Debug (not recommended), see output description for further
details
• General Options/ Numeric; except for the Residual Stress Analysis,
these options are infrequently used:
 Residual Stress Analysis is invoked if a positive value is entered
which limits the number of trials. An entry of „1“ allows for the
maximum of 100 trial analyses (often more realistic for slender,
elastic piles than normal analyses); a value between 1 and 100
specifies the maximum number of trial analyses.
 Hammer gravity modifies static weight of assembly and helmet; it is
normally set to the full gravitational value unless consideration is
given to bouyancy or pile inclination.
 Pile gravity normally set to the full gravitational value; may be set to
zero which is the traditional option for bearing graphs or to a reduced
value if the pile is subject to buoyancy or inclination.
 Time Increment Ratio in percent; may be reduced if there is a
possibility of numerical instability; use a value greater than 160, e.g.
300.
 Number of Iterations; see description of numerical procedure.
Normally not modified.
 Round Out deformations for hammer and pile cushions; rarely
modified.
 Analysis Duration, though generally set automatically, may
sometimes be of interest for durations chosen longer than standard
analysis.
• General Options/ Stroke pertains only to diesel hammers;
 Convergence of stroke with fixed pressure
 Convergence of pressure with fixed stroke
 Single analysis with fixed stroke and pressure
 Stroke Convergence Criterion
 Fuel Setting
• Pile Parameters, to override certain hammer file data (Options,
Hammer Parameters)
 Pile Segment Option, for direct input of the segment length,
stiffness, and weight of the pile model; generally, this is a somewhat
laborious procedure and it is easier to let the computer calculate
these numbers.
 Splices, accepts input of the number of splices, their depth, slack
distance, round-out deformation, and coefficient of restitution.
 Additional Input
- Coefficient of restitution for the pile top spring;
- Round Out for the pile top spring;
 Pile Profile Section Input (see P1 input form)
• Soil Parameters
 Soil Segment Damping/Quake for entering relative static resistance
values and quakes for each segment; click first on Simple
Resistance Distr. and then Detailed Resistance Distribution.

- No Individual soil segment input (default)
- Individual damping input for each segment
 Extended Soil Model
- Toe Model (for research only)
- Radiation Damping Model (for research only)
• Hammer Parameters to override certain hammer file data (Options,
Hammer Parameters)
 Stroke can also be changed on Main Screen
 Efficiency can also be changed on Main Screen
 Reaction Weight for closed ended diesel hammers,
 Diesel hammer combustion parameters:
- Combustion Pressure can also be changed on Main Screen
- Combustion Delay for liquid fuel injection hammers negative to
model preignition
- Ignition Volume for atomized injection hammers
 Vibratory hammer parameters:
- Vibratory Frequency can also be changed on Main Screen
- Vibratory Delay, time over which hammer is allowed to reach full
frequency
- Line force, positive if it reduces the weight effect of the hammer;
negative if it pushes down (creates a crowd force).
 Assembly Weight for external combustion hammers (these
hammers are sometimes equipped with special guides or sleeves
which increases the total assembly weight supported by pile and soil
prior to impact.
 Offshore opens up the offshore input window; for Offshore Wave
Version only.
 - Pipe Pile Add-on Input for offshore pipe piles considering add-on
properties (Elastic modulus, Specific weight, Critical section
index, Length, Cut-off). Also includes an option for generation an
Stabbing Guide model.
 - Inclination, allows for the input of the batter (inclination) angle
input and calculates and then allows for input of gravity reduction,
stroke reduction and efficiency reduction. The angle of inclination
input is also necessary for the static bending analysis.
 - Hammer, allows for modifying the point on the pile where hammer
drives the pile: top, intermediate or bottom location.
 - Jacket Template accepts the input necessary (Water Depth and
Height of Pile support point of Template/Jacket) for above the
mudline for the static pile bending analysis.
EXAMPLE
This example demonstrates a step-by-step solution for a basic case using

only the Main Input Form for input including:
Simple shaft resistance distribution,

Uniform pile,
Bearing graph or Inspector's Chart analysis,
and Hammer information contained in the hammer data file.

I. Data input
Collect all relevant information using the Pile and Driving Equipment Form
(Form 1 in Chapter 4). You may have to find driving system and pile
material properties in the appropriate help files (performed during program
execution).
1. Click on New Icon and enter the project title and file name with directory
path. Click Next.
2. To select a hammer either enter the Hammer ID No. – if known – or

search the hammer list until the desired hammer is found. You may
organize the listing by clicking on the heading to be sorted (e.g. view
alphabetic order of hammer manufacturers by clicking on Name). Click
on the desired hammer line or select the hammer manufacturer’s name
for an abbreviated listing of the associated hammers. Click Next.
3. Select the analysis type, in our case, the bearing graph analysis option.
Let us assume that the uncertainty for end bearing and shaft resistance
is equal. Then we can choose the default bearing graph option with
proportionally increasing shaft resistance and end bearing. For most
bearing graph analyses, the proportionally increasing skin friction/end
bearing option is satisfactory. (If the shaft resistance were well known,
like when a pile is driven to a hard layer, the constant shaft resistance
method may be more appropriate and if the end bearing were better
known than the shaft resistance, then the constant end bearing analysis
should be chosen). Click Next.
4. Select the pile top material (note that a concrete pile driven with a steel
follower would require the Steel selection). If Concrete is chosen, the
pile cushion properties must also be specified in this box. Pressing the
F3 function key with the cursor on the pile cushion elastic modulus will
bring up a table with cushion material properties. If the cursor is on the
cushion area field, selecting F3 will bring up the area calculator.
The program will also require entry of pile toe area and pile perimeter;
these values are needed for use with the static geotechnical analyses
(ST, SA, CPT or API). For displacement piles (concrete; closed ended
pipes), the toe area is easily determined; for H-piles and for open end
pipe piles with diameters 20 inches (500 mm) or less, it may be
assumed that the piles behave like plugged displacement piles, and the
toe area is therefore the full gross area. For larger open ended pipe
piles (say greater than 30 inches in diameter), the assumption may be
made that the piles are coring (not plugging). In that case, the toe area
is that of the steel cross section. Please note that even though
dynamically the large diameter pipes may not plug, it is often assumed
that they plug under static loads. Plugging is a complex problem as it
depends on the pile penetration, the soil type, the soil density, pile
penetration into dense layers and other factors and cannot be dealt with

in a simple example demonstration such as this (see also Section
3.13.6).
The input of a pile penetration is also required. This value may already
be known from a previously performed static soil analysis or it will be
established during the subsequent analysis. In the latter case an initial
guess (maybe 2 ft or.0.5 m less than the total pile length) is satisfactory.
Click Next.
5. Enter hammer cushion and helmet weight information. This may be

done directly or after clicking on function key F3 and making selections
from the PDI data collection. If no driving system data is available for the
chosen hammer make, the data of a similar hammer can be chosen in a
first analysis attempt. Obviously though, it would be best to obtain the
correct information from either the hammer supplier or the contractor.
Click Next.
6. The next step allow for a very simple soil input for a granular or cohesive
input. If a more detailed analysis is desired, that can be done after the
input wizard is finished. Click Next.
7. The program displays the resistance distribution and dynamic soil

resistance parameters. The user should review and if necessary make
corrections. Click Next.
8. The program displays 10 ultimate capacity values. They were selceted

based on the pile impedance (size and material properties). These may
be changed, but they are probably OK for a first analysis attempt. Clieck
Next.
9. After reading the input wizard’s comments, Click Finish.
10.The completed main input form displays the data submitted. Review the
important hammer performance parameters shown below the hammer
selection screen. In particular, check whether the efficiency and/or
hammer stroke or energy setting are appropriate (for battered/inclined
piles go to Options, Pile Parameters, Pile Batter/Inclination. Stroke
may be important if the hammer is used with a reduced energy setting
and Pressure is an important parameter for diesel hammer analyses,
particularly if the hammer is to be operated with a reduced fuel setting.
11. Review pile data such as length and cross sectional area and change
(as explained earlier), if necessary. Also check the standard pile
material parameters (e.g. the elastic modulus and/or the specific weight)
assigned when the pile material was chosen. For example, a high
strength concrete may have a higher modulus than the default value
(the Help offers a pile mateial table).

12. Find out the required design load (usually information is provided in the
Pile and Driving Equipment Form) and the required factor of safety. The
factor of safety depends among other things on the manner in which the
pile bearing capacity is verified (static, dynamic testing, etc.), the quality
of the pile installation method, the variability of the soil, the type of
structure for which the foundation is built, and other important
considerations. In general, if capacity determination is based on wave
equation analysis alone, i.e. without other test results or measurements,
factors of safety may vary between 2.5 and 3.0. A standard
recommendation cannot be given here. More on this important subject
may be found in Hannigan et al. (2006).
Multiply the design load by the factor of safety to obtain the required
Ultimate Capacity. Be sure that the 10 Ultimate Capacity values
chosen by the program include the values that are important for the
present project.
For a useful Bearing Graph, it is recommended to include enough

points in the calculation both below and above the required ultimate
capacity such that a smooth bearing graph can be plotted. You may
click on Reset, enter a capacity increment and then click on the first
capacity input field to fill all ten values or click on Action and then
Automatic to fill the array with reasonable values. For concrete piles, be
sure to include small ultimate capacity values to find critical tension
stresses. High capacity values allow for a check of compression
stresses and the driveability limit of the hammer-pile-soil system.
II. Check status
Before submitting the data set for analysis, it should be checked for
completeness. After clicking Options, Check Status, a message will be
display which either indicates satisfactory or incomplete input data
preparation.
III. Save input data
Click on the Save Input data icon. (Be sure that the file name and path are
satisfactory – Save Input File As under File may also be used.)
IV. Perform analysis
Click on the A (for analysis) icon. Preliminary output will be displayed. This
screen should be closed as soon as it is no longer needed, i.e. after an
initial result check.
V. Inspect numerical output
Click on the O (for output) icon to enter the output selection screen. View
the calculated results in the *.GWO file by clicking on Numerical Output.
Particular attention should be given to the hammer model, driving system

parameters, and pile model. The complete output should also be checked
for any program performance messages. They may indicate a problem with
the calculated output. Should there be a problem indicated, make changes
to the input data by exiting the Numerical Display and by clicking on the
Main Screen Icon. The Numerical output is often printed and included in
reports. Read and be aware of the disclaimer. When finished with this
inspection, exit the numerical display and return to the output selection
screen.
VI. Generate output
In addition to the numerical output, you may want to generate a graphical or

numerical summary output. For our simple example, this means, in general,
plotting of the Bearing Graph and a tabulation of the numerical bearing
graph results. Click on Bearing Graph in the Output Selection Screen.
Both a graph and a numerical result table will be displayed. Enlarge one or
the other (upper right hand corner). Return to both displays by selecting
dual display (upper right hand corner). Changes to scales can be done in
View, Ranges. The bearing graph can be interpreted as to the required
blow count for a desired bearing capacity, or it can be interpreted for the
capacity corresponding to an observed blow count. Associated with the
capacity is, for the same blow count, a maximum compression stress and,
important for concrete piles, a maximum tensile stress. The stress maxima
may occur anywhere along the pile.
After inspecting and possibly printing (or after View, Copy to Clipboard
pasting in a report document) the bearing graph output, exit the bearing
graph program.
If you are curious about certain calculated output variables, click on

Variables in the Output Selection Screen. Certain curves and display
modes may be selected in View, Ranges and Selections. This program is
self-explanatory. Note that you may have to change your variables in
Options, General Options, Output to get the desired results.
You may return to the main screen and run a second example and then plot
two results in the same bearing graph. (The second bearing graph can be
nd
chosen after clicking on File, Read 2 file.) This ends the demonstration
of a simple bearing graph example.
VII. More frequently used options
For Non-uniform piles: Click on th the Pile Option drop down menu and
click on Non Uniform Pile and then enter the pile properties (Cross
sectional area, Elastic modulus, Specific weight, Pile Perimeter, Critical
Stress Index) at all depth values where changes occur in the so-called P1
input form.

Soil Resistance Distribution: The Simple Resistance Distribution is
probably an exception and, unless the ST, SA, CPY, or API static soil
analyses have been performed, it is often necessary to enter a Variable
Resistance Distribution. For bearing graph analyses, only relative
magnitudes must be entered because the total capacity and the percentage
shaft resistance are addtional inputs. Thus, the relative resistance
distribution values will be multiplied by the shaft resistance percentage and
the analyzed ultimate capacity to yield the shaft resistance. The remainder
is the end bearing. In contrast, the Detailed Resistance Distribution
requires input of relative capacity values for every segment of the pile
model. This is a rarely used option.
Bearing Graph options: Instead of doing a bearing graph analysis with

proportionally changing friction and end bearing components, the analysis
options Constant Friction or Constant End Bearing options may be
selected. In the former case, the friction percentage will be applied to the
first capacity analyzed and then only the end bearing will be increased. In
the latter case, the end bearing will be the same for all analyses (see also
Section 4.5, Options, Analysis Options.
Additional Analysis Options: The Inspector's Chart option analyzes only

one capacity for up to 10 different stroke (energy) values. Be sure to specify
a reasonable stroke in the appropriate field below the hammer selection
screen, as a low starting value. Depending on the numerical value of the
starting stroke either full stroke or ½ m stroke increments will be used, or
the program interpolates nine strokes between this minimum and maximum
values of the hammer data file. If a diesel hammer is analyzed, it may also
be of interest to review the hammer stroke option (see Options, General
Options, Stroke).
Pile Options: Splices in piles, if they allow for some forceless deformation,
are input through Options, Pile Parameters, Splices.
Numerical analysis: The Residual Stress Analysis is (or has to be )

frequently performed when the pile is realtively flexible. The option is
activated after selecting Options, General Options, Numerical and then
entering a number between 1 and 100. Enter "1" to perform a residual
stress analysis with up to 100 trials for convergence. Enter a number
greater than 1 to limit the maximum number of trial analyses.
VIII. Less frequently used input options
Pile Segment Input Option is for the input of individual values for mass,
stiffness, and relative segment length for each segment of the pile model
(Options, Pile Parameters, Pile Segment Option). Note that the
corresponding pile profile input is necessary for non-uniform piles.
Soil Segment Input is for the input of individual quakes, damping factors
(Options, Soil Parameters, Soil Segment Damping/Quake), and ultimate
resistance values at each segment (Detailed Resistance Distribution

from the Soil Resistance Distribution drop-down menu). Quakes can only
be individually entered together with the static resistance distribution after
choosing Detailed Resistance Distribution in the resistance distribuion
drop down menu. Damping input is not dependent on that option.
The Soil, Pile, and Hammer Damping Options are accessible through
Options, General Options, Damping. Usually these options are of little
help, except the soil damping option which should be set to Smith viscous
for Residual Stress Analyses and for Vibratory Hammer analyses.
Any one of the Numerical options (Options, General Options, Numerical),

except the Residual Stress Analysis, is rarely used.
Not used in practice is the Extended Soil Model for the activation and use of
non-standard soil models; this is only recommended for research (Options,
Soil Parameters, Extended Soil Model).
IX. About Help for GRLWEAP
Click on Help and Help Topics and an index will open that links the user to
all available help files. These files make up the complete Users Manual of
GRLWEAP. For example, tables of hammers, efficiency reductions, setup
factors, driving system parameters, etc. are included. Also, there are many
links between these files to aid in navigation. In addition, the Help Section
provides many example problems including descriptions of input
preparation and output interpretation. Numerical results of these examples
can be viewed by opening the *.GWO file. Please take some time to study
the various documents within the help (and maybe print them out for your
printed manual) prior to using the program.
As previously explained, direct help, i.e., direct entry of data in certain input
fields is also available. Once the cursor is on such an input field, press F3
to activate the Help feature.

Appendix D: The GRLWEAP Friction Fatigue Approach
An Offshore Wave Option
GRLWEAP 2010-6 Offshore Wave offers two means of calculating SRD: (a)
the standard which is a uniform reduction of resistance in each soil layer
based on setup factor(s) and Gain/Loss factors and (b) an exponentially
varying approach which is related to Heerema, (1980) and, for example,
Alm and Hamre (2001).
In the following we refer to “Friction Fatigue” and it should be absolutely

clear that it has nothing to do with the fatigue damage that may occur in the
pile material due to pile driving.
The uniform (standard) GRLWEAP approach calculates the static

resistance to driving (SRD) as:
SRDi = LTSRi/fsi (D1)
where LTSR is the long term static resistance as calculated by a static

approach and i refers to a particular pile segment. Within this uniform setup
method, GRLWEAP also offers a time/distance variable resistance setup
and resistance loss approach which considers soil setup during a driving
interruption to increase logarithmically with time and a related loss of
resistance developing linearly with driving depth following the driving
interruption. All segments along the pile are affected proportionally to their
setup potential in this approach using a so-called limit distance, Lli, which
can be different for each segment i. Thus the setup resistance is assumed
to have vanished and the soil resistance being again at the SRD level when
the pile has been driven a distance Lli. This approach works fairly well for
short distances, but it does not work well when losses of resistances occur
over a greater distance of driving which would require that Lli is much
greater than the length of one or two pile segments.
The second method, developed at the end of 2013, combines features of

the basic GRLWEAP setup factor approach with those proposed by, for
example, Alm and Hamre (2001).This friction fatigue approach assumes
that pile driving causes little loss of shaft soil resistance near the toe but a
much higher resistance loss closer to the seabed where the pile shaft has
already done much more work on the soil and between the pile toe and a
certain distance (we use again the term Limit Length) above the toe the
shaft resistance decreases exponentially.
For the Modified Friction Fatigue approach, let us introduce a friction

reduction factor, ffi, and designate as z the distance of the center point of a
segment measured from the pile toe. We calculate the resistance on the
shaft of a pile segment as
SRDi = LTSRi * ffi (D2)
where

ffi = 1/fsi for z ≥ (1 + fL) Lli (D3)
i.e., fully reduced resistance for pile segments above Limit Length plus
bottom section
ffi = 1 for z ≤ fL Lli (D4)
i.e., full resistance over a distance fL Lli above the pile toe and
(αi z*)
ffi = 1/fs - fo + x1 e for fL Lli ≤ z ≤ (1 + fL) Lli (D5)
i.e., exponentially varying in between. The coordinate z* is zero at a

distance fL Lli above the pile toe and therefore
z* = z - fL Lli (D6)
Also,
x1 = 1 – [(1/fs) - fo] (D7)
and
αi = ln[fo/x1] / Lli (D8)
The factor fo defines the shape of the exponential function (see Figure 1).
The factor fL allows for an unreduced resistance over a distance above the
bottom (the “bottom section”) which is equal to f L Lli. Both fo and fL are the
same for all soil layers. However, Lli and fsi can be chosen differently for the
various soil layers.
GRLWEAP applies the following limits
fo ≤ 0.9(1/fsi ) (D9)
and
fo ≥ 0.001 (D10)
also the setup factor of any soil layer i has to be greater than 1 (GRLWEAP
would replace a value less than 1 with 1 without warning):
fsi ≥ 1 (D11)
The user should be aware of the following :
 Only one G/L factor < 1 can be analyzed with this approach and it must
be the first shaft G/L factor. Also the first shaft G/L should be the
inverse of the largest setup factor fsi for a meaningful calculation. If it
were 1.0 then the LTSR would be analyzed (no friction fatigue) and that
may be conveniently be done with the second analysis and associated
nd
2 shaft G/L factor.
 Using the same setup factors, the total SRD calculated with this
method is lower than the SRD of the standard method; equivalent
setup factors are discussed below.

 Both wait time and the soil setup time inputs are ignored in this
analysis.
80
70 fL 0.1 fo 0.1
Distance from Bottom
60 fL 0.05 fo 0.001
50
40
30
20
10
0
0 0.5 1 1.5
Friction Fatigue Multiplier
Figure 1: Exp. Multiplier for fs=5, Limit Dist=50m,
Pile L=75m; fo=0.1 and 0.001 and fL=0.1 and 0.05
Potentially, the restriction of Equation (9) makes the f o factor different for
different soil layers. To explain, consider a clay with f s = 5 and a sand layer
with fs = 1.2. The restriction is then fo ≤ 0.18 for the clay and fo ≤ 0.84 for the
sand. However in general much lower fo values are used anyhow. The user
can choose both fo and fL.
Examples
In the first example let us consider a single uniform soil layer where the
LTSR of each 1 m long pile segment is 500 kN (10 m circumference and 50
kPa unit shaft resistance). Figure 2 shows how in Options/Offshore the
“Friction Fatigue” option was activated with fo set to 0.01 and with a bottom
section factor fL = 0.0 (which means over a distance of 0*Lli above the pile
toe the friction is constant and equal to LTSR). Figure 3 shows the
calculated resistance distribution for pile toe depths of 25, 50 and 75 m
(equivalent ot ½ Lli, Lli and 1.5 Lli since a limit length of Lli = 50 m had been
input in the S1 soil resistance table).
The shaft G/L was set to 0.2 corresponding to a setup factor of 5; the fully
reduced segment resistance is, therefore, 100 kN. The pile length was 100

m. The results plotted in Figure 3 show for the 1 m depth below mudline a
small resistance above the SRD, because the Lli is greater than the
penetration. For the deeper penetration of 50 and 75 m the resistance at 1
m is at the fully reduced value. Note that the bottom segment resistance is
never exactly equal to the full LTSR (in this case of fL = 0), because of the
finite pile segment length of 1 m (at 1 m above the bottom the resistance is
already reduced).
Figure 2: Friction Fatigue Option in the Offshore Wave Version of

GRLWEAP

Resistance per1 m segment in kN
0 100 200 300 400 500
0
10
20
Depth below mudline in m
30
40
50
60
70
80
25 m depth 50 m depth
90
75 m Depth
100
Figure 3: Uniform soil, 3 different depths,
Lli=50m, fo=0.01
The next example is for a two layer situation. It was assumed that a 50 m
sand layer with fs = 1.25 overlies a clay layer with f s = 5. The G/L was,
therefore, set to 0.2. Lli was set to 50 m for both layers. The LTSR for each
sand segment was 250 kN; that of the clay again 500 kN. Figure 4 shows
that at a depth of 50 m, the pile is still fully embedded in sand and
experiences resistance values between slightly more than 200 kN and 250
kN (with fs=1.25 the fully reduced resistance is 250/1.25=200 kN). Note
that once the pile reaches full depth, the sand resistance is practically
completely reduced while the clay layer shows characteristics as per the
first example. While Figure 4 shows the result with an f L = 0 (resistance loss
begins at the very bottom), Figure 5 shows the results with a 5% unreduced
bottom section.

Segment Resistance in kN
0 100 200 300 400 500 600
0
20
Depth Below Mudline in m
40 Depth = 50m
Depth = 75 m
Depth = 100 m
60
80
100
120
Figure 4: 100 m pile; 50 m sand with fs=1.25; over 50 m

clay with fs=5; Li=50m; fo =0.01; fL = 0.0

Segment Resistance in kN
0 200 400 600
0
20
Depth (m)
Depth Below Mudline in m
100
40 Depth (m)
75
60
80
100
120
Figure 5: 100 m pile; 50 m sand with fs=1.25; over 50 m

clay with fs=5; Li=50m; fo =0.01; fL =0.05

Relationship between standard and Friction Fatigue setup factors
Define the Friction Fatigue setup factor fsFf as the ratio of initial resistance
(near the bottom) to fully reduced resistance (Ll above the bottom).
Consider the following figure which is an example of a resistance
distribution for a Friction Fatigue setup factor of 4. It shows the resistance
distribution of over depth equal to the Limit Length. It can be shown that
the total skin friction, which is equal to the area between the resistance
distribution curve and the horizontal and vertical axes, is given by:
Ll
FS-Ff = x2 Ll +(x1/ α)(e - 1) (D12)
where x2 = 1/fs – fo; x1 = 1 – x2; and α = ln(fo / x1) / Ll.
The GRLWEAP shaft resistance over the same distance Ll is given by
FS-GW = LTSR / SRD = (finitial / fs) Ll (D13)
Ratio of residual/initial resistance

0 0.2 0.4 0.6 0.8 1
0
10
Percentage of Ll layer depth
20
30
40
50
60
70
80
90
100
Figure 6: Example of the friction fatigue factor (reduced/initial resistance)
vs. normalized depth assuming a Friction Fatigue setup factor f sFF=4.
Using the above formulas, we can now calculate for different shape factors
fo the Friction Fatigue setup factors which would yield the same total
Friction Fatigue shaft resistance as the standard GRLWEAP approach.
They are shown below both numerically and graphically. The resulting
setup factor conversions are shown in Figure 7 and Table 1. For example, if
fo = 0.001 (the curve farthest to the right) then to get the same total friction
in a layer (assuming the layer thickness and Ll are the same – which is
usually not true and that is a severe limitation of these results) then a

standard GRLWEAP setup factor of 3.14 corresponds to a Friction Fatigue
setup factor of 5.
Table 1: GW Standard Setup Factor vs Ff Setup Factors
Shape Factor (exponent), fo

Ff-Setup
0.001 0.002 0.004 0.006 0.008 0.01 0.02 0.05 0.075 0.1
F.
10.00 4.32 4.08 3.82 3.66 3.54 3.45 3.17 2.81 2.66 2.56
7.50 3.84 3.65 3.44 3.32 3.23 3.15 2.92 2.62 2.49 2.41
5.00 3.14 3.02 2.88 2.80 2.74 2.69 2.53 2.31 2.22 2.15
4.00 2.76 2.67 2.57 2.51 2.46 2.42 2.30 2.13 2.05 2.00
2.75 2.17 2.12 2.06 2.03 2.00 1.98 1.90 1.80 1.75 1.72
2.00 1.73 1.70 1.67 1.65 1.63 1.62 1.58 1.52 1.49 1.47
1.50 1.38 1.37 1.36 1.35 1.34 1.33 1.31 1.28 1.27 1.26
1.25 1.20 1.19 1.18 1.18 1.17 1.17 1.16 1.14 1.14 1.13
10.00
9.00
8.00
Ff Setup Factor
7.00
6.00
5.00
4.00
3.00
2.00
1.00
1.00 2.00 3.00 4.00
Standard GRLWEAP Setup Factor
fo=0.001 0.002 0.004 0.006
0.008 0.01 0.02 0.05
0.075 0.1
Figure 7: Friction Fatigue setup factors which would give the same total
shaft resistance as the standard setup factors for Ll = pile toe depth.

APPENDIX E: REFERENCES
Alm, T. and Hamre, L., (2001). Soil model for pile drivability predictions
th
based on CPT interpretation. Proc. of the 15 Int. Conf. on Soil Mechanics
and Geotechnical Engineering, 2, Istanbul, 1297-1302.
API, American Petroleum Institute, (1993). “Recommended Practice for

Planning, Designing and Constructing Fixed Offshore Platforms – Load and
Resistance Factor Design”, API Recommended Practice 2A-LRFD (RP 2A-
LRFD), First Edition, July 1, 1993. Reaffirmed 2003.
Blendy, M.M., (1979), "Rational Approach to Pile Foundation," Symposium

on Deep Foundations, ASCE National Convention.
Bowles, J.E. (1977). Foundation Analysis and Design. Second Edition,

McGraw-Hill Book Company, New York, 85-86.
Coyle, H.M., Bartoskewitz, R.E., and Berger, W.J., (1973), "Bearing

Capacity Prediction by Wave Equation Analysis - State of the Art," Texas
Transportation Institute, Research Report 125-8.
Fellenius, B.H. (1996). Basics of Foundation Design, a geotechnical

textbook and background to the UniSoft programs, BiTech Publishers Ltd.,
Richmond, B.C., Canada.
Forehand, P.W. and Reese, J.L., (1964), "Prediction of Pile Capacity by the
Wave Equation," Journal of the Soil Mechanics and Foundations Division,
ASCE, Paper No. 3820, SM 2.
Goble, G.G., Likins, G.E., and Rausche, F., (1975), "Bearing Capacity of
Piles From Dynamic Measurements," Final Report, Department of Civil
Engineering, Case Western Reserve University.
Goble, G.G. and Rausche, F., (1976), "Wave Equation Analysis of Pile
Driving-WEAP Program," Volumes 1 through 4, FHWA #IP-76-14.1 through
#IP-76-14.4.
Goble, G.G. and Rausche, F., (1981), "Wave Equation Analyses of Pile
Driving-WEAP Program," Volumes 1 through 4, FHWA #IP-76-14.1 through
#IP-76-14.4.
Goble Rausche Likins and Associates, Inc. (1997), "Diesel Hammer

Modeling for Wave Equation Analyses," from Background Report of the
WEAP87 Program, Cleveland, Ohio.
Hannigan, P.J., Goble, G.G., Likins, G.E.,and Rausche, F., (2006). "Design
and Construction of Driven Pile Foundations". Vol. I and II; Nat. Highway
Institute, Federal Highway Administration, US Department of
Transportation, Report No. FHWA-NHI-05-042; NHI Courses No. 132021
and 132022, Washington, D.C.

Heerema, E.P., (1980. Predicting pile drivability; Heather as an illustration
of the friction fatigue theory. Ground Engineering, 13(3), 15-37.
Hery, P., (1983), "Residual Stress Analysis in WEAP," Master's Thesis,

Department of Civil, Environmental, and Architectural Engineering,
University of Colorado.
Hirsch, T.J.Jr., Carr, L., and Lowery, L.L.Jr., (1976), "Pile Driving Analysis
Wave Equation User's Manuals - TTI Program," Volumes 1 through 4,
FHWA #IP-76-13.1 through #IP-76-13.4.
Holeyman, A., Vanden Berghe, J.-F., and Charue, N. (eds.), 2002. Vibratory
pile driving and deep soil compaction – TRANSVIB2002. Proc. of the Intern.
Conference; A.A. Balkema, Lisse, Abingdon, Exton, Tokyo, ISBN 90 5809
5421 5.
Holloway, D.M., Clough, G.W., and Vesic, A.S., (1978), "The Effect of
Residual Driving Stresses on Pile Performance Under Axial Loads," OTC
3306.
Jaky, J. (1944). “Coefficient of Earth Pressure at Rest”. J. Soc. Hungarian

Architects & Engineers: 355-358.
Kulhawy, F.H., Jackson, C.S., & Mayne, P.W. (1989) “First-Order

Estimation of Ko in Sands and Clays”, Foundation Engineering: Current
Principles and Practices, Vol. 1, Ed. F. H. Kulhawy, ASCE, New York, 121-
134.
Kulhawy, F.H. & Mayne, P.W. (1991). “Relative Density, SPT & CPT
Interrelationships”, Calibration Chamber Testing, Ed. A. –B. Huang,
Elsevier, New York, 197-211.
Lowery, L.L., Hirsch, T.J.Jr., and Samson, C.H., (1967), "Pile Driving
Analysis - Simulation of Hammers, Cushions, Piles and Soils," Texas
Transportation Institute, Research Report 33-9.
PDCA (2001), “Recommended design specifications for driven bearing

piles”, Third edition, Pile Driving Contractors Association, PO Box 1429,
Glenwood Springs, CO 81602.
Rausche, F., and Klesney, A., (2007). Hammer Types, Efficiencies and
Models in GRLWEAP. Annual Int. Conf., PDCA, Nashville, TN, USA.
Rausche, F., Likins, G.E., Goble, G.G., and Miner, R., (1985), "The
Performance of Pile Driving Systems," Main Report, Volume 1 through 4,
FHWA Contract # DTFH61-82-C-00059.

Rausche, F., Liang, L., Allin, R., and Rancman, D., 2004. Applications and
th
Correlations of the Wave Equation Analysis Program GRLWEAP. 7 Int.
Conf. on the Application of Stress Wave Theory to Piles, Kuala Lumpur.
Rausche, F., Likins, G.E., and Goble, G.G., (1994), "A Rational and Usable
Wave Equation Soil Model Based on Field Test Correlation," Proceedings,
Design and Construction of Deep Foundations, Federal Highway
Administration, Washington, D.C.
Rausche, F., Nagy, M., and Likins, G., (2008). “Mastering the Art of Pile
Testing”. Keynote lecture, The Eighth Int. Conf. on the Appl. of Stress Wave
Theory to Piles in Lisbon, Portugal.
Rausche, F, Nagy, M., Webster, S., and Liang, L., (2009), “CAPWAP and
Refined Wave Equation Analyses for Driveability and Capacity Assessment
th
of Offshore Pile Installations.”, Proc. of the ASME 28 Int. Conf. on Ocean,
Offshore and Arctic Eng., May 31-June 5, Honolulu, HI, USA. Paper No.
OMAE 2009-80163.
Robertson, P.K. & Campanella, R.G. (1983). “Interpretation of Cone

Penetration Tests: Sand”, Can. Geot. J., 20 (4), 718-733.
Robertson, P.K., Campanella, R.G., Gillespie, D. and Grieg, J. (1986). “Use

of Piezometer Cone Data.” Proceedings of In-Situ’86, ASCE Specialty
Conference, Use of In Situ Tests in Geotechnical Engineering, Special
Publication No. 6, Blacksburg, 1263-1280.
Samson, C.H., Hirsch, T.J.Jr., and Lowery, L.L., (1963), "Computer Study
for Dynamic Behavior of Piling," Journal of the Structural Division, ASCE,
Volume 89, No. ST4, Proc. Paper 3608.
Schmertmann, J. H. (1975). “Measurement of In-Situ Shear Strength”,

Proceedings of Conference on In Situ Measurement of Soil Properties,
ASCE, New York.
Schmertmann, J. H. (1978). Guidelines for Cone Penetration Test:

Performance and Design, FHWA-TS-78-209 (report), US Department of
Transportation, 145.
Skov, R. and Denver, H., (1988), "Time-Dependence of Bearing Capacity of

Piles," Proc. of the Third International Conference on the Application of
Stress-Wave Theory to Piles.
Smith, E.A.L., (1951), "Pile Driving Impact," Proceedings, Industrial

Computation Seminar, September 1950, International Business Machines
Corp., New York, N.Y., p. 44.
Smith, E.A.L., (1960), "Pile Driving Analysis by the Wave Equation," Journal
of the Soil Mechanics and Foundations Division, ASCE, Volume 86.

Thendean, G., Rausche, F., Svinkin, M., and Likins, G.E., (1996), "Wave
Equation Correlation Studies," Presented at the Fifth International
Conference on the Application of Stress Wave Theory to Piles in Orlando,
Florida.
Additional Recommended Reading
Coyle, H.M., and Gibson, G.C., (1970), "Empirical Damping Constants for
Sands and Clays," ASCE Journal of Soil Mechanics and Foundation
Division.
Hussein, M., Likins G.E., and Rausche, F., (1988), "Testing Methods of
Driving Piles", Pile Buck Annual Handbook/Directory of Pile Driving,
Foundation and Marine Construction Techniques, Engineers, Contractors,
Manufacturers, Distributors and Supplies.
Hussein, M., Rausche, F., and Likins, G.E., (1988), "Wave Equation
Analysis of Pile Driving: Methodology and Performance," Presented at 6th
National Conference on Microcomputers in Civil Engineering, Orlando,
Florida.

GRLWEAP 2010 Background

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

GRLWEAP 2010 Background

Uploaded by

Copyright:

Available Formats

GRLWEAP 2010 Background Report

Version 2010 GRLWEAP Procedures and Models i

ii GRLWEAP Procedures and Models Version 2010

Version 2010 GRLWEAP Procedures and Models iii

iv GRLWEAP Procedures and Models Version 2010

Version 2010 GRLWEAP Procedures and Models v

Throughout the development of this software package, PDI has strived to

1.2 Program History

GRLWEAP developed out of the WEAP program of 1976. The original

WEAP87 was developed, tested and documented under the sponsorship of

The GRLWEAP package prior to 1993 consisted of several executable files

Version 2010 GRLWEAP Procedures and Models 1

The 2003-2005 versions included among others the following modifications:

 Two static analysis methods were added to simplify the input of

 Copy and paste features were added to Depth/Modifier Input Form

 The hammer information was now organized in two separate

 Assembly Weight input was added to Hammer Override Dialog

 Rated and maximum diesel hammer stroke are distinguished. Diesel

 In the output programs the “Copy to Clipboard” command was added

2 GRLWEAP Procedures and Models Version 2010

GRLWEAP’s 2010 program version comes in two modules, the standard

Standard program features now include:

For static geotechnical analysis in addition to the ST and SA methods:

(b) a method based on API requirements.

For static geotechnical analysis, the SA method was modified as follows:

 In lieu of entering an SPT-N value, allow for an input of qu, the

 The SPT-N value input is now completed in the main SA window

 The graphics of the SA and ST input windows have been modified

For the analysis of inclined (battered) pile driving:

 The program now allows entering the inclination degree or ratio.

Improvements related to Driveability analysis include:

Version 2010 GRLWEAP Procedures and Models 3

 Also very important, in the S1 input form, a new column, Toe

 An automatic feature was added for generating an improved

 After the S1-table has been complete, Gain/Loss factors are

Allow to copy hammer/pile/soil model plot to other applications such as MS

Changed pile strength/yield input to a critical section index for a simple

4 GRLWEAP Procedures and Models Version 2010

 A Pipe Pile Builder for simplified input of complex pipe pile

1.4 The Wave Equation Approach

GRL's Wave Equation Analysis of Pile Driving is a program which simulates

 The blow count (number of hammer blows/unit length of

 The axial stresses in a pile, both tension and compression,

Version 2010 GRLWEAP Procedures and Models 5

Based on these results the following can be indirectly determined:

 The pile's bearing capacity at the time of driving or restriking,

 The stresses during pile driving, given an observed blow

 The expected blow count if the static bearing capacity of the

Of course, by varying the hammer type, driving system parameters

6 GRLWEAP Procedures and Models Version 2010

The concept of the dynamic formula is as follows:

where Es is the energy available to do work on the soil and sl represents

Es = Ek - Eds - Epl - Esl (2.2)

The hammer efficiency is a number between 0 and 1.

Modern hammers have an attachment called a helmet at the bottom of the

and the energy formula may be written as:

ed eh Er - Epl - Esl = Ru s (2.5)

Version 2010 GRLWEAP Procedures and Models 7

8 GRLWEAP Procedures and Models Version 2010

The computational procedure established by Smith again leads to a Bearing

Version 2010 GRLWEAP Procedures and Models 9

Tension Stress (MPa)

Figure 2.3: Inspector’s Chart from GRLWEAP

10 GRLWEAP Procedures and Models Version 2010