Unit 3: Continuity of a Function

Lesson 3.1
Continuity of a Function at a Point
Contents
Introduction 1

Learning Objectives 2

Warm Up 3

Learn about It! 4

Intuitive Definition of Continuity of a Function 5
Continuity of a Function at a Point Given Its Graph 5
Continuity of a Function at a Point Given Its Equation 11
Properties of Continuous Functions at a Point 18

Key Points 22

Check Your Understanding 23

Challenge Yourself 26

Photo Credits 26

Bibliography 27

Key to Try It! 27

Unit 3: Continuity of a Function

Lesson 3.1

Continuity of a Function at a Point

Introduction
Due to heavy traffic, commuters prefer the train as a means of transportation. Shown on the
map are the LRT and MRT stations in Metro Manila. It is convenient to go from one station
to another if all stations are in operation. In this situation, we can say that there is continuity
in your travel. On the other hand, if one station is experiencing a problem, you have no choice
but to go down from that station and continue to another one. In this situation, we can say
that your travel is not continuous.

3.1. Continuity of a Function at a Point 1

Unit 3: Continuity of a Function

Your travel is similar to graphs of functions. Some graphs are continuous, and some are not.
The station that experiences a problem is related to the point on the graph of a function
where continuity stops, and the way you continue your travel from that point is where you
continue to trace the graph after lifting it from this point. How can we determine if a function
is continuous at a given point?

Learning Objectives DepEd Competencies

In this lesson, you should be able to do the

● Illustrate continuity of a function at
following: a number
● Illustrate the continuity of a function (STEM_BC11LC-IIIc-1).

at a point. ● Determine whether a function is

continuous at a number or not
● Determine whether a function is
(STEM_BC11LC-IIIc-2).
continuous at a point or not using its
graph.
● Determine whether a function is
continuous at a point or not using its
equation.

3.1. Continuity of a Function at a Point 2

Unit 3: Continuity of a Function

Warm Up
Graphical Continuity 10 minutes
This activity will help you illustrate the continuity of a function at a point given its graph.

Materials
● laptop with an internet connection

Procedure
1. This activity should be done in groups of five to seven students sharing a laptop.
2. Graph the given functions using the link below.

Desmos. Graphing Calculator

Luberoff, Eli, “Graphing Calculator,”
Desmos, https://www.desmos.com/calculator, last accessed on
February 5, 2020.

a. 𝑓(𝑥) = 𝑥 3 − 𝑥 2 + 𝑥 + 1
𝑥 2 +𝑥
b. 𝑔(𝑥) =
𝑥+3
𝑥 − 7, if 𝑥 < 1
c. ℎ(𝑥) = { 2
𝑥 + 3, if 𝑥 ≥ 1

• If you are having a hard time graphing a piecewise function on Desmos, you
may refer to the following link.

“Piecewise.”
Luberoff, Eli, “Piecewise,”
Desmos, http://bit.ly/2tHvrZ2, last accessed January 26, 2020.

3. Observe the graph of each function and answer the guide questions individually.

3.1. Continuity of a Function at a Point 3

Unit 3: Continuity of a Function

Guide Questions
1. Try tracing each graph with your mouse cursor. Which among the functions where
you able to trace continuously?
2. In which graphs were you not able to trace continuously from left to right?
3. On those graphs that you were not able to trace continuously, on which point did the
graph break?
4. Which functions do you think are continuous, and which are not? Why?

Learn about It!

Recall from the previous lessons that there are functions whose limit as 𝑥 approaches 𝑐 is not
equal to the value of the function at 𝑐. In symbols, lim 𝑓(𝑥) ≠ 𝑓(𝑐).
𝑥→𝑐

𝑥 + 5, if 𝑥 < 1
Consider the function 𝑓(𝑥) = { 2 . Let us evaluate lim 𝑓(𝑥) and 𝑓(𝑐).
𝑥 − 1, if 𝑥 ≥ 1 𝑥→𝑐

lim 𝑓 (𝑥) = 𝑥 2 − 1
𝑥→1+

= (1)2 − 1
=0

lim 𝑓(𝑥) = 𝑥 + 5
𝑥→1−
= 1+5
=6

Since lim+ 𝑓(𝑥) ≠ lim− 𝑓(𝑥), lim 𝑓(𝑥) does not exist. Moreover,
𝑥→1 𝑥→1 𝑥→1

𝑓(1) = 𝑥 2 − 1
= 12 − 1
= 0.
What does this imply about the graph of 𝑓?

3.1. Continuity of a Function at a Point 4

Unit 3: Continuity of a Function

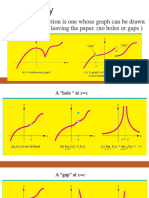
Intuitive Definition of Continuity of a Function

A function is said to be continuous if its graph has no breaks or holes, and you can trace it
without lifting your pen. A continuous function is defined for any real number.

Examples of continuous functions are illustrated below.

Fig. 3.1.1. Examples of continuous functions

Examples of graphs that are not continuous (or discontinuous) are illustrated below.

Fig. 3.1.2. Examples of discontinuous functions

Continuity of a Function at a Point Given Its Graph

While there are functions that are discontinuous, they could be continuous at some points.
Any function 𝑓(𝑥) is said to be continuous at a point 𝑥 = 𝑐 if you can trace the graph from the
left going to the right of 𝑐 without lifting your pen.

3.1. Continuity of a Function at a Point 5

Unit 3: Continuity of a Function

Consider the graph of the function 𝑓 (𝑥) = 3𝑥 − 2 as follows.

Fig. 3.1.3. Graph of 𝑓 (𝑥) = 3𝑥 − 2

The function is said to be continuous at 𝒙 = 𝟐 if you can trace the graph from the left going
to the right of 𝑥 = 2 without lifting your pen. Since you can trace the graph without lifting
your pen at 𝑥 = 2, 𝑓(𝑥) = 3𝑥 − 2 is continuous at 𝒙 = 𝟐.

𝑥 2 +𝑥−6
Let us consider the function 𝑓 (𝑥) = 𝑥+3
.

𝑥 2 +𝑥−6
Fig. 3.1.4. Graph of 𝑓 (𝑥) = 𝑥+3

3.1. Continuity of a Function at a Point 6

Unit 3: Continuity of a Function

Notice that we cannot trace the graph of the function from the left of 𝑥 = −3 going to its right
since there is a hole in the graph, and we lift our pen in this hole to continue tracing the
𝑥 2 +𝑥−6
graph. Thus, 𝑓 (𝑥) = 𝑥+3
is discontinuous at 𝒙 = −𝟑.

Let’s Practice!

Example 1
Determine if the graph below is continuous at 𝑥 = 3 and 𝑥 = 0.

Solution
First, plot the given points on the graph at 𝑥 = 3 and 𝑥 = 0. Then, determine if it is
continuous or not by tracing the graph from left going to the right at these points.

3.1. Continuity of a Function at a Point 7

Unit 3: Continuity of a Function

Notice that we can trace the graph without lifting the pen from the left going to the right of
𝑥 = 3. Thus, the function is continuous at 𝒙 = 𝟑. On the other hand, at 𝑥 = 0, we lift our pen
from the left going to its right to continue tracing the graph. Hence, the function is
discontinuous at 𝒙 = 𝟎.

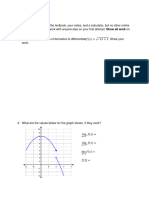
1 Try It!
Determine if the graph below is continuous at 𝑥 = −1 and 𝑥 = 2.

Example 2
Is the graph below continuous at 𝑥 = 2, 𝑥 = −3, and 𝑥 = 4?

3.1. Continuity of a Function at a Point 8

Unit 3: Continuity of a Function

Solution
First, plot the given points on the graph at 𝑥 = 2, 𝑥 = −3, and 𝑥 = 4. Then, determine if it is
continuous or not by tracing the graph from the left going to the right at these points.

By inspection, we can see that there is no point on the graph at 𝑥 = 2 because it is the vertical
asymptote. Thus, we lift our pen to trace the graph continuously from the left going to the
right at this asymptote, making the graph discontinuous at 𝒙 = 𝟐. On the other hand, we can
trace the graph from the left going to the right at 𝑥 = −3 and 𝑥 = 4. Thus, the function is
continuous at 𝒙 = −𝟑 and 𝒙 = 𝟒.

3.1. Continuity of a Function at a Point 9

Unit 3: Continuity of a Function

2 Try It!
1
Is the graph below continuous at 𝑥 = 1, 𝑥 = − 2, and 𝑥 = −5?

Example 3
Determine if 𝑓(𝑥) = √𝑥 − 1 is continuous at 𝑥 = 2.

Solution
The graph of the given function is shown as follows.

3.1. Continuity of a Function at a Point 10

Unit 3: Continuity of a Function

Notice that we can trace the graph without lifting the pen from the left going to the right of
𝑥 = 2. Thus, the function is continuous at 𝒙 = 𝟐.

3 Try It!
1
Determine if 𝑓(𝑥) = (𝑥−3)2 is continuous at 𝑥 = 3.

How can we determine if a function is continuous

at a given point without tracing its graph?

Continuity of a Function at a Point Given Its Equation

A function 𝑓 is said to be continuous at the number 𝑐 if and only if the following conditions
are satisfied:

1. 𝑓(𝑐) exists;
2. lim 𝑓(𝑥) exists, and
𝑥→𝑐

3. lim 𝑓(𝑥) = 𝑓(𝑐).

𝑥→𝑐

If at least one of these conditions fails to hold at 𝑐, the function is said to be discontinuous
at 𝑐. Discontinuous functions will be discussed in detail in Lesson 3.3.

Using the formal definition of continuity of a

function at a point, what functions are
automatically continuous everywhere?

3.1. Continuity of a Function at a Point 11

Unit 3: Continuity of a Function

Let’s Practice!

Example 4
Determine if 𝑓(𝑥) = 2𝑥 2 − 6𝑥 + 2 is continuous at 𝑥 = −3.

Solution
Step 1: Determine the value of 𝑓(𝑐) and lim 𝑓(𝑥), where 𝑐 = −3.
𝑥→𝑐

𝑓 (𝑥) = 2𝑥 2 − 6𝑥 + 2
𝑓 (−3) = 2(−3)2 − 6(−3) + 2
= 2(9) + 18 + 2
= 18 + 20
= 38

lim 𝑓 (𝑥) = 2(−3)2 − 6(−2) + 2

𝑥→−3
= 2(9) + 18 + 2
= 18 + 20
= 38

Step 2: Check if the conditions are satisfied.

Since 𝑓(𝑥) is defined at 𝑥 = −3, lim 𝑓(𝑥) exists, and 𝑓 (−3) = lim 𝑓(𝑥) = 38, it
𝑥→−3 𝑥→−3

follows that 𝒇(𝒙) is continuous at 𝒙 = −𝟑.

4 Try It!
Determine if ℎ(𝑥) = 3𝑥 3 − 4𝑥 2 + 𝑥 − 5 is continuous at 𝑥 = 4.

3.1. Continuity of a Function at a Point 12

Unit 3: Continuity of a Function

Example 5
2𝑥−3
Is 𝑔(𝑥) = 𝑥 2 +4𝑥+4 continuous at 𝑥 = −2?

Solution
Determine the value of 𝑔(𝑐) and lim 𝑔(𝑥), where 𝑐 = 1.
𝑥→𝑐

2𝑥 − 3
𝑔(𝑥) =
𝑥 2 + 4𝑥 + 4
2(−2) − 3
𝑔(−2) =
(−2)2 + 4(−2) + 4
−4 − 3
=
4−8+4
−7
=
0
= undefined

Since 𝑔(𝑐) is undefined, there is no need to get the limit of the function as 𝑥 approaches 𝑐.
Therefore, 𝒈(𝒙) is discontinuous at 𝒙 = −𝟐.

5 Try It!
𝑥−5
Is ℎ(𝑥) = 𝑥 2 +5𝑥+6 continuous at 𝑥 = 5?

Is a rational function continuous everywhere? Why

or why not?

3.1. Continuity of a Function at a Point 13

Unit 3: Continuity of a Function

Tips
We can easily determine if polynomial functions or rational
functions are continuous at a point. Remember the following
guidelines:
• If 𝑓(𝑥) is a polynomial function, then 𝑓(𝑐) is always defined
for any 𝑐 and lim 𝑓(𝑥) = 𝑓(𝑐). Thus, polynomial functions
𝑥→𝑐

are continuous at any point.

𝑃(𝑥)
• If 𝑓 (𝑥) = is a rational function, then lim 𝑓(𝑥) = 𝑓(𝑐)
𝑄(𝑥) 𝑥→𝑐

provided that 𝑄(𝑐) ≠ 0, which implies that 𝑐 is not in the

domain of 𝑓. Thus, rational functions are only continuous
in their respective domains.

Example 6
|𝑥 − 2 |, if 𝑥 ≠ 2
Determine if 𝑓(𝑥) = { is continuous at 𝑥 = 2.
5, if 𝑥 = 2

Solution
Step 1: Graph the function.

3.1. Continuity of a Function at a Point 14

Unit 3: Continuity of a Function

Step 2: Determine if 𝑓(𝑐) exists.

Let 𝑐 = 2. Based on the graph, if 𝑥 = 2, then 𝑦 = 5. Thus, 𝑓(2) = 5.

Thus, 𝑓(𝑐) exists and is equal to 5.

Step 3: Determine if lim 𝑓(𝑥) exists.

𝑥→𝑐

Let us solve for both lim− 𝑓(𝑥) and lim+ 𝑓(𝑥).

𝑥→2 𝑥→2

Based on the graph, lim− 𝑓(𝑥) = 0 and lim+ 𝑓(𝑥) = 0. Since lim− 𝑓(𝑥) = lim+ 𝑓(𝑥),
𝑥→2 𝑥→2 𝑥→2 𝑥→2

it follows that lim 𝑓(𝑥) exists and is equal to 0.

𝑥→2

Step 4: Determine if lim 𝑓(𝑥) = 𝑓(𝑐).

𝑥→𝑐

In the given problem, lim 𝑓(𝑥) = 0 and 𝑓(𝑐) = 5. Since lim 𝑓(𝑥) ≠ 𝑓(𝑐), it follows
𝑥→2 𝑥→2
|𝑥 − 2 |, if 𝑥 ≠ 2
that 𝑓 (𝑥) = { is discontinuous at 𝑥 = 2.
5, if 𝑥 = 2

6 Try It!
𝑥 2 − 1, if 𝑥 < −1
Determine if 𝑓(𝑥) = { is continuous at 𝑥 = −1.
√𝑥 + 1, if 𝑥 ≥ −1

Example 7
𝑥+3
Find the value or values of the constant 𝑘 so that 𝑓(𝑥) = 𝑥 2+5𝑥−7𝑘 is continuous at 𝑥 = −3.

Solution
Since we would like to know the value of 𝑘 that makes 𝑓(𝑥) continuous at 𝑥 = −3, we must
solve for the value of 𝑘 that will satisfy the three conditions for continuity.

3.1. Continuity of a Function at a Point 15

Unit 3: Continuity of a Function

Step 1: Determine the value of 𝑘 such that 𝑓(𝑐) does not exist.

Let 𝑐 = −3. We are certain that 𝑓(𝑐) does not exist if the denominator is equal
to zero as it would make 𝑓(𝑐) undefined. Thus, let us equate 𝑥 2 + 5𝑥 − 7𝑘 as 0
with 𝑥 = −3 and solve for 𝑘.

𝑥 2 + 5𝑥 − 7𝑘 = 0
(−3)2 + 5(−3) − 7𝑘 = 0
9 − 15 − 7𝑘 = 0
−6 − 7𝑘 = 0
−7𝑘 = 6
6
𝑘=−
7

6
Step 2: Interpret the value of 𝑘 = − .
7

6
This means that at 𝑘 = − 7, 𝑓(−3) is undefined. For any values of 𝑘, 𝑓(−3) is

defined. Since 𝑓(𝑥) is a rational function, we know that as long as 𝑐 is in the

domain of 𝑓(𝑥), 𝑓(𝑥) is continuous at 𝑐.

𝟔
Therefore, 𝑓(𝑥) is continuous at 𝑥 = −3 as long as 𝒌 ≠ − 𝟕.

7 Try It!
5
For what value or values of 𝑘 is 𝑓 (𝑥) = (7+𝑘)𝑥−3 continuous at 𝑥 = −3?

3.1. Continuity of a Function at a Point 16

Unit 3: Continuity of a Function

Example 8
𝑥+7
2𝑘𝑥 2 −5𝑘
, 𝑥 < −8
𝑥+3
Find the value/s of the constant 𝑘 so that 𝑓 (𝑥) = , −8 ≤ 𝑥 ≤ 5 is continuous at
𝑥 2+5𝑥−7𝑘
𝑥
, 𝑥>5
{ 2𝑘−18

𝑥 = −3.

Solution
Step 1: Determine which “piece” of 𝑓(𝑥) is needed to evaluate 𝑓(𝑐) and lim 𝑓(𝑥).
𝑥→𝑐

𝑥+3
Since 𝑥 = −3 falls on the interval −8 ≤ 𝑥 ≤ 5, we use 𝑓(𝑥) = to evaluate
𝑥 2+5𝑥−7𝑘

𝑓(−3). Likewise, for lim 𝑓(𝑥), we use the same “piece” because the arbitrary
𝑥→−3

values that are close to the left and right of 𝑥 = −3 fall on the same interval.

𝑥+3
Step 2: Evaluate the denominator of 𝑓(𝑥) = at 𝑥 = −3.
𝑥 2 +5𝑥−7𝑘

𝑥 2 + 5𝑥 − 7𝑘 = (−3)2 + 5(−3) − 7𝑘
= 9 − 15 − 7𝑘
= −6 − 7𝑘

Step 3: Equate −6 − 7𝑘 to 0 and solve for 𝑘.

−6 − 7𝑘 = 0
−7𝑘 = 6
6
𝑘=−
7

𝑥+3 6
Hence, 𝑓(𝑥) = 𝑥 2 +5𝑥−7𝑘 is defined at 𝑥 = −3 when 𝑘 ≠ − 7.

3.1. Continuity of a Function at a Point 17

Unit 3: Continuity of a Function

Step 4: Determine the value of 𝑘.

From the previous steps, we have the following true statements:

6
• 𝑓(𝑐) is defined when 𝑘 ≠ − 7.
6
• lim 𝑓(𝑥) = 𝑓(𝑐) when 𝑘 ≠ − (based on Theorem 2.2.2).
𝑥→−3 7

𝒙+𝟕
, 𝒙 < −𝟖
𝟐𝒌𝒙𝟐 −𝟓𝒌
𝒙+𝟑
Based on these statements, we conclude that 𝑓 (𝒙) = , −𝟖 ≤ 𝒙 ≤ 𝟓 is
𝒙𝟐 +𝟓𝒙−𝟕𝒌
𝒙
{ 𝟐𝒌−𝟏𝟖
, 𝒙>𝟓
𝟔
continuous at 𝒙 = −𝟑 for any real values of 𝒌 except − 𝟕.

8 Try It!
1
𝑥 4 + 2𝑘𝑥 + 1, 𝑥 < − 2
5 1
For what value/s of 𝑘 is 𝑓 (𝑥) = (7+𝑘)𝑥−3
, 𝑥 > − 2 continuous at 𝑥 = −3?
8𝑥 1
{(𝑥+5)𝑘+3𝑘𝑥 2 , 𝑥 = −2

Properties of Continuous Functions at a Point

The following properties can be observed about the continuity of a function at a point.

Property 1: 𝑓(𝑥) + 𝑔(𝑥) is continuous at 𝑐.

Proof: Suppose 𝑓(𝑥) and 𝑔(𝑥) are both continuous at 𝑥 = 𝑐. Thus, lim 𝑓(𝑥) = 𝑓(𝑐) and
𝑥→𝑐

lim 𝑔(𝑥) = 𝑔(𝑐).

𝑥→𝑐

lim [𝑓(𝑥) + 𝑔(𝑥)] = lim 𝑓 (𝑥) + lim 𝑔(𝑥)

𝑥→𝑐 𝑥→𝑐 𝑥→𝑐
= 𝑓 (𝑐) + 𝑔(𝑐)

3.1. Continuity of a Function at a Point 18

Unit 3: Continuity of a Function

Property 2: 𝑓(𝑥) − 𝑔(𝑥) is continuous at 𝑐.

Proof: Suppose 𝑓 and 𝑔 are both continuous at 𝑥 = 𝑐. Thus, lim 𝑓(𝑥) = 𝑓(𝑐) and
𝑥→𝑐

lim 𝑔(𝑥) = 𝑔(𝑐).

𝑥→𝑐

lim [𝑓(𝑥) − 𝑔(𝑥)] = lim 𝑓 (𝑥) − lim 𝑔(𝑥)

𝑥→𝑐 𝑥→𝑐 𝑥→𝑐
= 𝑓 (𝑐) − 𝑔(𝑐)

Property 3: 𝑓(𝑥) ∙ 𝑔(𝑥) is continuous at 𝑐.

Proof: Suppose 𝑓 and 𝑔 are both continuous at 𝑥 = 𝑐. Thus, lim 𝑓(𝑥) = 𝑓(𝑐) and
𝑥→𝑐

lim 𝑔(𝑥) = 𝑔(𝑐).

𝑥→𝑐

lim [𝑓(𝑥) ⋅ 𝑔(𝑥)] = lim 𝑓 (𝑥) ⋅ lim 𝑔(𝑥)

𝑥→𝑐 𝑥→𝑐 𝑥→𝑐
= 𝑓 (𝑐) ⋅ 𝑔(𝑐)

𝑓(𝑥)
Property 4: is continuous at 𝑐, provided that 𝑔(𝑐) ≠ 0.
𝑔(𝑥)

Proof: Suppose 𝑓 and 𝑔 are both continuous at 𝑥 = 𝑐. Thus, lim 𝑓(𝑥) = 𝑓(𝑐) and
𝑥→𝑐

lim 𝑔(𝑥) = 𝑔(𝑐).

𝑥→𝑐

lim 𝑓 (𝑥)
𝑓 (𝑥) 𝑥→𝑐
lim =
𝑥→𝑐 𝑔(𝑥) lim 𝑔(𝑥)
𝑥→𝑐
𝑓 (𝑐)
= , 𝑔(𝑐) ≠ 0
𝑔(𝑐)

3.1. Continuity of a Function at a Point 19

Unit 3: Continuity of a Function

Let’s Practice!

Example 9
𝑥+3
Using the properties of the continuity of a function at a point, determine if 𝑓 (𝑥) = is
𝑥−2

continuous at 𝑥 = 0.

Solution
Let 𝑔(𝑥) = 𝑥 + 3 and ℎ(𝑥) = 𝑥 − 2. Since 𝑔(𝑥) and ℎ(𝑥) are polynomial functions, we can say
𝑔(𝑥)
that both 𝑔(𝑥) and ℎ(𝑥) are continuous at 𝑥 = 0. In this case, 𝑓 (𝑥) = is continuous at
ℎ(𝑥)

𝑥 = 0 only when ℎ(0) ≠ 0. With this in mind, let us verify if ℎ (0) = 0.

ℎ(𝑥) = 𝑥 − 2
ℎ(0) = 0 − 2
= −2

𝑥+3
Since ℎ (0) = −2 and not equal to 0, we can say that 𝑓(𝑥) = 𝑥−2 is continuous at 𝑥 = 0.

9 Try It!
Using the properties of the continuity of a function at a point, determine if
𝑓 (𝑥) = (𝑥 + 3)3 is continuous at 𝑥 = −3.

3.1. Continuity of a Function at a Point 20

Unit 3: Continuity of a Function

Example 10
𝑔(𝑥)
If 𝑓 and 𝑔 are both polynomial functions, is 𝑓(𝑥) + 𝑓(𝑥) always continuous at 𝑥 = 𝑐 for any 𝑐?

Why or why not?

Solution
Since 𝑓 and 𝑔 are both polynomial functions, 𝑓 and 𝑔 are continuous everywhere, and 𝑓(𝑐)
and 𝑔(𝑐) are both defined.

𝑔(𝑥)
However, it is possible that the function 𝑓(𝑥) + is not continuous at 𝑥 = 𝑐 if 𝑓(𝑐) = 0. Thus,
𝑓(𝑥)
𝑔(𝑥)
𝑓 (𝑥) + 𝑓(𝑥) is not always continuous at 𝑥 = 𝑐.

10 Try It!
Given that 𝑓(𝑥) and 𝑔(𝑥) are both continuous at 𝑥 = 𝑐, determine if
𝑓 (𝑥) ⋅ 𝑔(𝑥) + [𝑓 (𝑥) + 𝑔(𝑥)]2 is always continuous at 𝑥 = 𝑐.

Example 11
The functions 𝑓 and 𝑔 are rational functions such that 𝑓 is continuous at 𝑥 = 𝑐 and 𝑔 is
continuous at 𝑥 = 𝑑. Is 𝑓(𝑥) + 𝑔(𝑥) always continuous at 𝑥 = 𝑐 + 𝑑? Why?

Solution
1 1
Consider 𝑓(𝑥) = 𝑥 and 𝑔(𝑥) = 𝑥+1. Since 𝑓(𝑥) and 𝑔(𝑥) are rational functions, 𝑓(𝑥) and 𝑔(𝑥) are
1
continuous in their respective domains. Thus, we can say that 𝑓 (𝑥) = is continuous at
𝑥
1
𝑐 = −1 and 𝑔(𝑥) = is continuous at 𝑑 = 0. Thus, 𝑓(𝑐) and 𝑔(𝑑) are both defined.
𝑥+1

Let us determine if 𝑓(𝑐 + 𝑑) + 𝑔(𝑐 + 𝑑) is defined. Note that 𝑐 + 𝑑 = −1 + 0 = −1.

3.1. Continuity of a Function at a Point 21

Unit 3: Continuity of a Function
1 1
For 𝑓(𝑥) = , 𝑓(−1) is defined. However, for 𝑔(𝑥) = , 𝑔(−1) is not defined. Thus, this means
𝑥 𝑥+1

that at 𝑐 + 𝑑 = −1, 𝑓 (𝑐 + 𝑑) + 𝑔(𝑐 + 𝑑) is not defined.

Therefore, 𝑓 (𝑥) + 𝑔(𝑥) is not always continuous at 𝑥 = 𝑐 + 𝑑.

11 Try It!
If 𝑓 and 𝑔 are both rational functions that are continuous at 𝑥 = 𝑐, is [𝑓(𝑥)]2 + 𝑔(𝑥)
always continuous at 𝑥 = 𝑐? Why?

Key Points
_____________________________________________________________________________________________

● A function 𝑓 is said to be continuous at the number 𝑐 if and only if the following

conditions are satisfied:
○ 𝑓(𝑐) exists;
○ lim 𝑓(𝑥) exists, and
𝑥→𝑐

○ lim 𝑓(𝑥) = 𝑓(𝑐).

𝑥→𝑐

● If at least one of these conditions fails to hold at 𝑐, the function is said to be

discontinuous at 𝑐.
● If 𝑓(𝑥) and 𝑔(𝑥) are both continuous at 𝑥 = 𝑐, then the following properties can be
observed:
○ 𝑓 (𝑥) + 𝑔(𝑥) is continuous at 𝑐;
○ 𝑓 (𝑥) − 𝑔(𝑥) is continuous at 𝑐;
○ 𝑓 (𝑥) ⋅ 𝑔(𝑥) is continuous at 𝑐, and
𝑓(𝑥)
○ 𝑔(𝑥)
is continuous at 𝑐, provided that 𝑔(𝑐) ≠ 0.

_____________________________________________________________________________________________

3.1. Continuity of a Function at a Point 22

Unit 3: Continuity of a Function

Check Your Understanding

A. Determine if the graph is continuous or discontinuous at the

given points.

For 1-2, refer to the graph below.

1. 𝑥 = −5
1
2. 𝑥 =
3

3.1. Continuity of a Function at a Point 23

Unit 3: Continuity of a Function

For 3-6, refer to the graph below.

3. 𝑥 = −1
4. 𝑥 = 2
5. 𝑥 = 1
6. 𝑥 = −3

For 7-10, refer to the graph below.

3.1. Continuity of a Function at a Point 24

Unit 3: Continuity of a Function
1
7. 𝑥 =
3
1
8. 𝑥 = 5

9. 𝑥 = −2
5
10. 𝑥 = 2

B. Determine if the following functions are continuous or discontinuous

at 𝑥 = 𝑐.

1. 𝑓(𝑥) = 𝑥 3 − 5𝑥 2 + 5𝑥 + 1; 𝑥 = √2
2 1
2. 𝑓(𝑥) = 𝑥 2 − 𝑥 + 5; 𝑥 = −3
3 5
𝑥 3 +3𝑥 2 −𝑥−3
3. 𝑓(𝑥) = 𝑥+1
; 𝑥 = −1
6𝑥 2 +𝑥−2 1
4. 𝑓(𝑥) = 2𝑥−1
; 𝑥 = −2
𝑥 2 +6𝑥−7
5. 𝑔(𝑥) = 𝑥 2 −𝑥−6
; 𝑥=3
𝑥2
6. ℎ(𝑥) = 2𝑥 2 +17𝑥+8; 𝑥=8
2𝑥 + 3, if 𝑥 ≤ 3
7. 𝑓(𝑥) = { ; 𝑥 = −3
𝑥 − 5, if 𝑥 > 3
𝑥+5
, if 𝑥 ≠ 2
8. 𝑓(𝑥) = {𝑥+2 ; 𝑥 = 10
5, if 𝑥 = 2
𝑥 2 + 1, if 𝑥 < 4
9. ℎ(𝑥) = { 3 − 𝑥, if 4 ≤ 𝑥 ≤ 6; 𝑥=4
2𝑥 2 − 8, if 𝑥 > 6
3𝑥 3 + 4𝑥 2 − 5𝑥, if 𝑥 ≤ −5
3𝑥−7
10. ℎ(𝑥) = { 𝑥−4
, if − 5 < 𝑥 < 9; 𝑥=2
𝑥+8
𝑥 3−4𝑥 2 +8𝑥
, if 𝑥 ≥ 9

3.1. Continuity of a Function at a Point 25

Unit 3: Continuity of a Function

C. Find the value of the constant 𝑘 so that the following functions are
continuous at 𝑥 = 𝑐.

4𝑥 3 −2𝑥+3
1. 𝑓(𝑥) = 5𝑘𝑥 2 −3𝑥+𝑘−2; 𝑥 = −7
10
2. ℎ(𝑥) = 2𝑥𝑘 2−2𝑘𝑥+1; 𝑥=2

Challenge Yourself

Read the following questions and answer them briefly.

1. Let 𝑓(𝑥) and 𝑔(𝑥) be polynomial functions. Determine if the function [𝑓(𝑥)]2 − [𝑔(𝑥)]2
is continuous at any point 𝑐 and explain why.
2. Suppose 𝑔(𝑥) is a polynomial function and ℎ(𝑥) is a rational function that are both
continuous at 𝑥 = 𝑐. Determine if 𝑓 (𝑥) = 𝑔(𝑥) ⋅ ℎ(𝑥) + 𝑔(𝑥) is continuous at 𝑥 = 𝑐.
Explain why.
3. Consider the function 𝑓(𝑥) = √𝑥. Is 𝑓(𝑥) continuous at any point 𝑐? Explain why.
4. Determine the points where 𝑔(𝑥) = tan(𝑥) is not continuous.
5. Create a piecewise function where 𝑓(𝑥) is continuous at any point 𝑥 = 𝜋.

Photo Credits
Manila LRT-MRT Map by Michael Gonzalez is licensed under CC BY-SA 3.0 via Wikimedia
Commons.

3.1. Continuity of a Function at a Point 26

Unit 3: Continuity of a Function

Bibliography
Dawkins, Paul. “Continuity.” Paul’s Online Notes. Accessed from
http://tutorial.math.lamar.edu/Classes/CalcI/Continuity.aspx, January 18, 2020.

Edwards, C.H., and David E. Penney. Calculus: Early Transcendentals. 7th ed. Upper Saddle
River, New Jersey: Pearson/Prentice Hall, 2008.

Leithold, Louis. The Calculus 7. New York: HarperCollins College Publ., 1997.

Larson, Ron and Edwards, Bruce. Calculus. United States of America: Brooks/Cole, Cengage
Learning, 2010.

Smith, Robert T., and Roland B. Milton. Calculus. New York: McGraw Hill, 2012.

Tan, Soo T. Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach.
Australia: Brooks/Cole Cengage Learning, 2012.

Key to Try It!

1. The graph is continuous at 𝑥 = 2 but not at 𝑥 = −1.
1
2. The graph is continuous at 𝑥 = − 2 and at 𝑥 = −5 but not at 𝑥 = 1.

3. The function 𝑓(𝑥) is discontinuous at 𝑥 = 3.

4. The function ℎ(𝑥) is continuous at 𝑥 = 4.
5. The function ℎ(𝑥) is continuous at 𝑥 = 5.
6. The function 𝑓(𝑥) is continuous at 𝑥 = −1.
7. 𝑓(𝑥) is continuous for all real values of 𝑘 except for 𝑘 = −8.
8. all real numbers
9. Let 𝑔(𝑥) = 𝑥 + 3. It follows that 𝑓 (𝑥) = 𝑔(𝑥) ⋅ 𝑔(𝑥) ⋅ 𝑔(𝑥). Since 𝑔(𝑥) = 𝑥 + 3 is

3.1. Continuity of a Function at a Point 27

Unit 3: Continuity of a Function

continuous at 𝑥 = −3, it follows that 𝑓(𝑥) is continuous at 𝑥 = −3 according to the

properties of the continuity of a function.
10. Let ℎ(𝑥) = 𝑓 (𝑥) ⋅ 𝑔(𝑥) and 𝑝(𝑥) = 𝑓(𝑥) + 𝑔(𝑥). Since 𝑓 and 𝑔 are both continuous at
𝑥 = 𝑐, it follows that 𝑓(𝑐) and 𝑔(𝑐) are both defined. According to the properties of
the continuity of a function at a point, both ℎ(𝑥) and 𝑝(𝑥) are continuous at 𝑥 = 𝑐.
11. Let 𝑚(𝑥) = [𝑝(𝑥)]2 . It follows that 𝑚(𝑥) = 𝑝(𝑥) ⋅ 𝑝(𝑥). This means that 𝑚(𝑥) is also
continuous at 𝑥 = 𝑐. Finally, let 𝑛(𝑥) = ℎ(𝑥) + 𝑝(𝑥). By the properties of the continuity
of a function at a point, it follows that 𝑛(𝑥) is continuous at 𝑥 = 𝑐.

3.1. Continuity of a Function at a Point 28