Linear Programming

Linear Programming:
Graphical Method
Libeeth B. Guevarra
Daisy A. Romeo
Department of Mathematics and Natural Sciences
Math031 - Mathematics in the Modern World 1

Formulation of Linear Programming Models
Define the specific decision variables

This is assigning variables to the given products
Identify the objective function which is either to maximize or to
minimize. This is the objective that you are trying to achieve in
solving the problem.
List down the constraints that affect the decision. There are
different types of constraints which can be found on a given
word problem solving:
a) Capacity Constraints - These are limitations on the amount of
eqquipment, space, or stuff availability.

b) Market Constraints - These are limitations (either lower or upper
limits or both) on how much upper can be sold or used.
c) Availability Constraints - These are limitations on the available raw
materials, labor, funds or other resources.
d) Quality or Blending Constraints - These are limitations on the
mixes of ingredients, usually defining the output of products.
e) Production Technology or Material Balance Constraints - These
are limitations that define the the output of some process, as the
function of the inputs, often loss for scrap.
f) Definitional Constraints - These are constraints that define a given
variable, often, such constraints came from accountancy definitions.

Illustration
1. A clock maker makes two types of wood clock to sell at various
malls. It takes him 3 hrs. to assemble a pine clock, which requires 2
oz of varnish. It takes 4 hrs. to assemble a molave clock, which takes
4oz of varnish. He has 8oz of varnish available in stock and he can
work 12 hrs. If he makes P100 profit on each pine clock and P120 on
each molave clock, how many each type should he make to maximize
his profit?

Step 1: Define the specific variables
(most of the time variables will answer the question being asked in
the problem)
In our example the question is ”how many each type should he make
to maximize his profit?” Thus our variables are the number of each
type of wood clock since the question is how many
Let x be the number of pine clock
y be the number of molave clock.

Step 2: Identify the objective function
This is the objective that you are trying to achieve in solving the
problem.
Objective: maximize profit
Convert the above statement into mathematical expression. Overall
prrofit is equal to profit of each type times quantity, we have
Profit := P = 100x + 120y (1)

Step 3: List all constraints
This sentence tells us the limitation of the production, ”He has 8oz
of varnish available in stock and he can work 12 hrs.” Thus the
constraints are varnish and production time.
For varnish:
Each pine clock consumed 2 oz and since we assumed that x pine are
to be produced so we need 2x oz of varnish for pine clock. And each
molave clock also need 4oz of varnish, so we need 4y oz of varnish
for the production of molave clocks. Total oz of varnish needed is
2x + 4y , but he only have 8oz of varnish available, which means that
our consumption of varnish should not go beyond 8oz (2x + 4y ≤ 8).

For production time:
It takes 3hrs for each pine clocks so we 3x hrs for all pine clocks.
And each molave clock takes 4hrs., so we need 4y hrs. to produce all
molave clocks. Total number of hours needed is 3x + 4y , but he can
only work for 12 hrs., which means that the total number of hours
should not go beyond 12hr. (3x + 4y ≤ 12).
Also variables x and y are quantities, so it should not be less than
zero (x ≥ 0 and y ≥ 0).

Linear Programming - Model

P be the profit
Objective: Maximize P = 100x + 120y
Constraints:
3x + 4y ≤ 12 Production Time
2x + 4y ≤8 Material or varnish
x ≥0
y ≥0

Illustration
2. A small generator burns two types of fuel: low sulfur and high
sulfur to produce electricity. For one hour, each gallon of low sulfur
emits 3 units of sulfur dioxide, generates 4kilowatts elecricity and
costs P160. Each gallon of high sulfur emits 5 units of sulfur dioxide,
generates 4 kilowatts and costs P150. The environmental protection
agency insists that the maximum amount of sulfur dioxide that can
be emitted per hour is 15 units. Suppose that at least 16 kilowatts
must be generated per hour, how many gallons of high sulfur and low
sulfur must be utilized per hour in order to minimize cost of fuel?

Define variable:
how many gallons of high sulfur and low sulfur must be utilized per
hour in order to minimize cost of fuel?
Let x be the number of gallons of high sulfur
y be the number of gallons of low sulfur.
Objective: minimize cost of fuel
each gallon of high sulur costs P150 and each gallon of low sulfur
costs P160
Cost := C = 150x + 160y (2)

”...the maximum amount of sulfur dioxide that can be emitted per
hour is 15 units. Suppose that at least 16 kilowatts must be
generated per hour...”
Constraints:
amount of sulfur dioxide emitted per hour
electricity generated per hour

”For one hour, each gallon of low sulfur emits 3 units of sulfur
dioxide, generates 4kilowatts elecricity and costs P160. Each gallon
of high sulfur emits 5 units of sulfur dioxide, generates 4 kilowatts
and costs P150.”
Constraints:
amount of sulfur dioxide emitted per hour: 5x + 3y ≤ 15
(less than or equal 15 because 15 is the maximum no. of units)
electricity generated per hour: 4x + 4y ≥ 16
(greater than or equal to since the minimum requirement is 16)
Also variables x and y are quantities, so it should not be less than
zero
(x ≥ 0 and y ≥ 0).


C be the cost of fuel.
Objective: Minimize C = 150x + 160y
Constraints:
4x + 4y ≥ 16 electricity generated per hour

5x + 3y ≤ 15 amount of sulfur dioxide emitted per hour
x ≥0
y ≥0

Graphical Solution to Linear Programming
Problems
Linear Programming problems involve a system of Linear Inequalities

with some constraints on it. A point satisfying the constraints of a
linear programming problem is called a feasible solution and the set
of all feasible solution is called the feasible region. The extreme
points of the feasible region is the possible solution of the linear
programming problem.

Illustration
1. A clock maker makes two types of wood clock to sell at various
malls. It takes him 3 hrs. to assemble a pine clock, which requires 2
oz of varnish. It takes 4 hrs. to assemble a molave clock, which takes
4oz of varnish. He has 8oz of varnish available in stock and he can
work 12 hrs. If he makes P100 profit on each pine clock and P120 on
each molave clock, how many each type should he make to maximize
his profit?


P be the profit
Objective: Maximize P = 100x + 120y
Constraints:
3x + 4y ≤ 12 Production Time
2x + 4y ≤8 Material or varnish
x ≥0
y ≥0

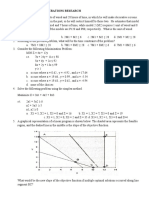
Feasible Region
The extreme points are: (0,2), (4,0) and (0,0)

To determine the solution to the problem
Extreme points P = 100x + 120y

(0,2) P=100(0)+120(2) = 240
(4,0) P=100(4)+120(0) = 400
(0,0) P=0
Since our objective is maximize profit, then choose the point (4,0)
because it gives tha maximum value.
∴ 4 pine clocks must be produced in order to get a maximum profit
of P400.

Illustration
2. A small generator burns two types of fuel: low sulfur and high
sulfur to produce electricity. For one hour, each gallon of low sulfur
emits 3 units of sulfur dioxide, generates 4kilowatts elecricity and
costs P160. Each gallon of high sulfur emits 5 units of sulfur dioxide,
generates 4 kilowatts and costs P150. The environmental protection
agency insists that the maximum amount of sulfur dioxide that can
be emitted per hour is 15 units. Suppose that at least 16 kilowatts
must be generated per hour, how many gallons of high sulfur and low
sulfur must be utilized per hour in order to minimize cost of fuel?


C be the cost of fuel.
Objective: Minimize C = 150x + 160y
Constraints:
4x + 4y ≥ 16 electricity generated per hour

5x + 3y ≤ 15 amount of sulfur dioxide emitted per hour
x ≥0
y ≥0

Feasible Region
The extreme points are: (0,4), (0,5) and (1.5,2.5)

To determine the solution to the problem

(0,4) P=150(0)+160(4) = 640
(4,0) P=150(4)+160(5) = 800
(1.5,2.5) P=150(1.5)+160(2.5) = 625
Since our objective is minimize cost, then choose the point (1.5,2.5)
because it gives tha minimum cost.
∴ 1.5 gal. of high sulfur and 2.5 gal. of low sulfur must be utilized
per hour to obtain the minimum cost of P625.

Example:
1. A farmer has 40 hectares of farm on which to plant rice and corn.
The rice needs 4 units of insecticide and two units of fertilizer per
hectare, while corn requires 3 units of insecticide and 6 units of
fertilizer. He has at least 90 units of insecticide and atleast 120 units
of fertilizer available. His average profit per hectare on rice is
P15,000.00 and P10,000.00 on corn. How many hectares of each
crop should he plant to maximize his average profit?

Let x be the number of hectares to be planted with rice.

y be the number of hectares to be planted with corn
P be the average profit.
Objective: Maximize P = 15, 000x + 10, 000y
Constraints:
x +y ≤ 40 area to be planted
4x + 3y ≥ 90 amount of insecticide
2x + 6y ≥ 120 amount of fertilizer
x ≥0
y ≥0

Verify the extreme points of set of constraints
Extreme points P = 15, 000x + 10, 000y

(0,30) P=15,000(0) +10,000(30) = 300,000
(0,40) P=15,000(0) +10,000(40)=400,000
(10,16.67) P=15,000(10) +10,000(16.67)=316,700
(30,10) P=15,000(30) +10,000(10)=550,000
∴ 30 hectares of land to be planted with rice and 10 hectares of land

to be planted with corn to obtain a maximum average profit of
550,000.

Example:
2. RFC company manufactures two types of lamps: special lamp and
regular lamp. Each special lamp requires 4 pounds of brass and each
regular lamp requires 8lbs of brass. During each production period,
the company’s brass supply is limited to 640lbs. Each special lamp
requires 6 hrs of milling time in the machines and each regular lamp
requires 2hrs. of milling time in the machines. The company’s
machines are available only for 360 hrs. in each production period.
Each special lamp requires 5 light bulbs that must be imported from
Hongkong. The importation of these bulbs is limited to 200 units.
The contribution to profit of each special lamp is P400 and P360 on
the regular lamp. How many units of the special lamp and regular
lamp should be produced per production period in order to maximize
the profit?

Let x be the number of special lamps.

y be the number ofregular lamps
P be the average profit.
Objective: Maximize P = 400x + 360y Constraints:
4x + 8y ≤ 640 brass requirement

6x + 2y ≤ 360 milling time
5x ≤ 200 light bulbs
x ≥0
y ≥0

Verify the extreme points of set of constraints

(0,0) P = 400(0) +360(0)= 0
(0,80) P = 400(0) +360(80)=28,800
(40,60) P = 400(40) +360(60)=37,600
(40,0) P = 400(40) +360(0)=16,000
∴ 40 units of special lamps and 60 units of regular lamps to be

produced per production period to have a maximum profit of
P37,600.

source:
Quantitative Approaches in Decision-Making by Arao et. al.

Linear Programming

Uploaded by

Document Information

Original Description:

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Linear Programming

Uploaded by

Copyright:

Available Formats

Linear Programming:

Math031 - Mathematics in the Modern World 1

Define the specific decision variables

Math031 - Mathematics in the Modern World 2

Math031 - Mathematics in the Modern World 3

Math031 - Mathematics in the Modern World 4

Math031 - Mathematics in the Modern World 5

Profit := P = 100x + 120y (1)

Math031 - Mathematics in the Modern World 6

Math031 - Mathematics in the Modern World 7

Math031 - Mathematics in the Modern World 8

Let x be the number of pine clock

Math031 - Mathematics in the Modern World 9

Math031 - Mathematics in the Modern World 10

Math031 - Mathematics in the Modern World 11

Math031 - Mathematics in the Modern World 12

Math031 - Mathematics in the Modern World 13

Let x be the number of gallons of high sulfur

4x + 4y ≥ 16 electricity generated per hour

Math031 - Mathematics in the Modern World 14