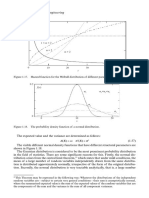
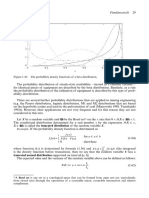
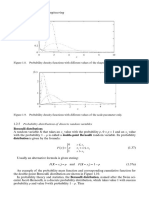
Fundamentals 37

It is said that an estimator Tn of parameter θ is unbiased if its expected value is the same as
the value of the estimated parameter30, i.e.

E(Tn) = θ (1.91)

Notice that the expected value of a random variable is a deterministic value31.

An unbiased estimator allows the unknown parameter to be estimated without systematic
errors.
The difference:

Δ = E(Tn) – θ (1.92)

is called a bias of the estimator Tn. Obviously, the bias of an unbiased estimator is zero.
Let us consider the estimation of an unknown expected value m in a certain general popu-
lation . Let us use the arithmetic mean formula:

1 n
x= ∑ xi .
n i=1
(1.93)

This estimator is an unbiased one since:

⎛ 1 n ⎞ 1 n 1
E (x ) = E ⎜ ∑ ⎟⎠ = n ∑ E(( )= nm = m
⎝ n i=1
i i
i=1 n

The second statistical parameter used most frequently, besides the expected value, is the
standard deviation σ or its square—the variance. Presume now that for the estimation of the
unknown variance σ2 of the general population, the following estimator was applied:

1 n
s2 ( ) = ∑ (x
n i =1
( xi x )2 (1.94)

Let us test the bias of the estimator above. Here we have:

⎡1 n ⎤ ⎧1 n ⎫
E [ s 2 ( X )] = E ⎢ ∑ (x ( xi x )2 ⎥ = E ⎨ ∑ [( xi m ) ( x m )]2 ⎬
⎣ n i =11 ⎦ ⎩ n i =1 ⎭
⎡1 n 1 n
⎤
= E ⎢ ∑ ( xi − m )2 − 2( x − m ) ∑ ( xi − m ) + ( x − m )2 ⎥
⎣ i =1
n n i =1 ⎦
1 n 1 n 2 1 2 n −1 2
= ∑ E[(x xi m − E x − m = ∑ σ − σ = σ ≠ σ2
n i =1 n i =1 n n

Thus, the above estimator is a biased one. Its bias is:

n −1 2 1
E [ s 2 ( X )] − σ 2 = σ − σ2 = − σ2
n n

30
There are more general notions of bias and unbiasedness. Here ‘bias’ is de facto ‘mean-bias’ in order
to distinguish mean-bias from the other notions with the most noteworthy ones being ‘median-unbiased’
estimators. See for example Rojo (2012).
31
In some statistical investigations, a randomisation of the expected value is made, i.e. we treat that value
as a random variable although this is a targeted exception from the rule.

Book.indb 37 12/9/2013 12:22:44 PM