ACTIVITY NO.

2
NORMAL DISTRIBUTION AND ITS APPLICATION

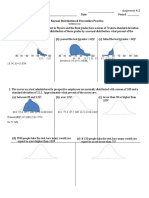
1. Suppose Z is a standard normal variable, in each of the following cases, find the value of
𝑎 if:
a. 𝑃(𝑍 < 𝑎) = 0.0026 (3 pts)
b. 𝑃(𝑍 < 𝑎) = 0.7994 (3 pts)
c. 𝑃(𝑍 > 𝑎) = 0.9335 (5 pts)
d. 𝑃(𝑍 > 𝑎) = 0. 4992 (5 pts)
2. If Z is a standard normal random variable, find the following probabilities:
a. 𝑃(𝑍 < 0.68) (3 pts)
b. 𝑃(𝑍 > 2) (5 pts)
c. 𝑃(−1.83 < 𝑍 < 2.5) (6 pts)
3. Given that a population of scores is normally distributed with 𝜇 = 100 and 𝜎 = 8,
determine the following: Illustrate the normal distribution and shade the appropriate
region.
a. the percentile rank of a score of 120; (5 pts)
b. the percentage of scores that are below a score of 99; (5 pts)
c. the percentage of scores that are between a score of 101 and 122; (10 pts)
d. the probability of scores that are between a score of 114 and 122. (10 pts)

4. At the end of a particular semester, Carol took four final examinations. The mean and
standard deviation for each exam along with Carol’s grade on each exam is listed here.
Assume that the grades in each exam are normally distributed.

Standard
Exam Mean Carol’s Grade
Deviation
Research 75.4 6.3 78.2
Statistics 85.6 4.1 83.4
Assessment 88.2 3.5 89.2
Competency
70.4 8.6 82.5
Appraisal
a. On which exam did Carol do best relative to the other students taking the exam? (20
pts)
b. What was her percentile rank on this exam? (5 pts)
5. Suppose X is normally distributed with a mean 𝜇 = 50 and standard deviation 𝜎 = 4.
In each case, indicate the given probability as an area under the normal curve and
determine its value.
a. 𝑃(𝑋 < 49) (5 pts)
b. 𝑃(𝑋 > 62) (5 pts)
c. 𝑃(44 < 𝑋 < 65) (5 pts)