SLAC-0007 CQ. , BLAC}{ Uc-28, Particle Accelerators and High-Voltage Machines Uc-34, Physics ‘TID=4500 SLAC-0007 AMA DESIGN AND FABRICATION OF THE ACCELERATING STRUCTURE FOR THE STANFORD TWO-MILE ACCELERATOR November 1962 by A. L. Eldredge, G. A. Loew, and R. B. Neal Stanford Linear Accelerator Center PEEDENGCE I1Cz EFERENCE USE Technical Report Prepared Under Contract AT(O4-3)-400 for the USAEC San Francisco Operations office Printed in USA. Price $2,00. Available from the Office of Technical Services, Department of Commerce, Washington 25, D.C.SUMMARY This report describes the principal factors affecting the design and fabrication of the accelerating structure that will be used for the Stanford two-mile linear electron accelerator. The structure will be an all-copper, cylindrical, disk-loaded waveguide, approximately four inches in diameter, and 10,000 eet long. When powered ty 240 klystron amplifiers, each operating at a peak pover of 24 megawatts, the accelerator will produce a 20-Bev electron ‘beam at an average beam current of 30 microamperes (10% beam loading). By in- creasing the number of klystrons to 960, should thie eventually be warranted, the beam energy could be increased to 40 Bev, and the average beam current to 60 microamperes. Although the traveling-wave accelerating structure described here is in general similar to that used vith previous Stanford machines, @ number of the structure's principal parameters are different. The operating frequency, 2856 Mc/sec, remains the same as earlier machines, as does the 10-foot in- terval between rf-power feed points along the machine. The rf pulse length of 2.5 usec and the pulse repetition rate of 360 pps result in a beam duty cycle approximately ten times greater than that of the present Stanford 1-Bev machine. Other differences from earlier machines are the selection of the 2n/3 operating mode rather than x/2; a constant-gradient structure rather than one with constent-attenuation; and e lower value of the attenustion para- meter in the structure (1 0.57 nepers). In addition to these parameters, the report describes the selection of accelerator length in relation to the total rf power required for a given bean energy. Final design of the accelerating structure is based on a synthesis of analytic and empirical findings together with consideration of the cost and practicality of fabrication and adjustment techniques. These letter factors are also described. A special furnace has been developed to assemble ten-foot sections of the accelerator by brazing. Final tuning of the individual accel- erator cavities (which are machined slightly oversize) will be accomplished by pressing permanent "dimples" into the cavity volume; the reliability of this dimpling technique 4s one of the principal factors making the brazing method of fabrication feasible. A second satisfactory method of fabrication, electro- forming, 1s also described.wv. TABLE OF CONTENTS Introduction eee a A, Mistorical review ©... 0... 00. B. General description 6... ee Selection of characteristic parameters... 2... Loe A. Choice of operating frequency so. ee B. Product of rf power and accelerator length... . 0... C. Selection of scceerator length .... 0... D. Selection of number of rf power sources and feed interval EB. Choice of rf pulse length ana repetition rate... . F. Selection of operating moe... . eee. a8 G. Constant-impedance vs constant-gredient structures... 2. 2) H. Choice of attenuation veremeter 2... 6 Eupirical design of the accelerator structure»... , 0... 42 A. Choice of the disk-loaded waveguide - 2... B. Definition and discussion of dimensions... 2... 1. ke €. Evolution of Stanford designs . 2... 2.1... eh D. Constent-gradient structure dimensions»... . 2.2... by E. Cold tests and corrections to achieve the empirical design . 48 F. Matehing and tuning of an accelerator section»... . . 58 G. Me coupler asyametry problem... ee 6 Fabrication techniques... 1 ee ee eBue ae. LIST OF FIGURES General view of accelerator and target area... .. 2. ++ Modular arrangement of ki stron, accelerator sections and connecting waveguide 6 6. eee Schenatic drawing of Gisk-loaded waveguide... 0.1 os Theoretica) and experimental curves of shunt impedance (74) per unit length vs number of disks per wavelength (n) for various disk thicknesses (t) «6 ee ee ee eee ee eee Theoretical and experimentel curves of Q vs number of disks per wavelength (n) for various disk thicknesses (t) cylinder dianeter of disk-losded waveguide as « function Coto Group velocity of aisk-loaded waveguide as a function of Cet Ratios of peak to average axial electric field strengtl in eonstant~impedance and constant~gradient accelerator Structures VET 6 ee ee Axial field strength vs t for equal electron energy gin in constant-gradient and constant-impedance sections GOOEY 6555555009 50055 50654 50Gs 5G Ratio of pover losses at input and output ends of accelerator section for constant-impedance and constant-gradient structures Unloaded beam energies for constant-impedance and constant gradient accelerator structures ve tT... ss Bean-losding derivatives for constant-impedance and constant-gradient accelerator structures VET Lev Neximun dean conversion efficiencies and corresponding values of peak bean current for constant~impedance and constant-gradient accelerators vs tT... 1. Frequency sensitivities of uniform and constant-gradient accelerator structures VET. ee ee Shapes of input and output rf pulses in e constant-gradient accelerator section (upper curves) and a constant impedance accelerator section (lower curves} 2... eee eee = it - Page 16 18 20 25 26 28 29 30 aL au20, a. 22. 23. 2h. 25, 26, 2. 28. 30. G8 Gingrans for the fundanentel TM, mode at the midpoint of = 10.foot constantagradient section and for the TM, node at the input, midpoint and output... Bean-loading curves for constant-gradient accelerator at various values of the attenuation parameter Te... Slow-wave structures designed for linear accelerators Traveling-wave electric £iel4 configurations for 0, «/2, 2n/3 and x phase shift per cavity... ee Brillouin diagrams for three different points in a typical constantgradient section... eee ee ee Variation of 20, 2a, v,/e, and the shunt impedance z, (corrected for the funtamental space harmonic) as a function of cav number along a 10-fect constant-gradient section foe 0e00 ee Variation of 2, 2a, v,/e, and the shunt impedance r, (corrected for the fundamentell space harmonic) as a function of cavity nunber ng a 10-foot constant-gradient section ort 10 ‘Typical experimental setup showing cavity stack used to obtain Brillouin diagram by successive resonances... . Typical cold-test setup showing cavity stacks and group- velocity variation as a function of length along constant-gradient section ©... ee eee Sketch of a ten-foot-long constant-gradient accelerator structure with input end output couplers... 0 ee Principle of the nodal shifting technique. Shown are cutaway section, copper plunger, and typical smith chart Smith chart plot cbteined in the coupler-matching technique Experimental arrangement for tuning a short accelerator section, with illustration of tuning tool ©... 2. Coupler asynmetry studies 2... eee Exploded view of parts assembled for the electroforming technique ee eee - aii - 35 37 43 45 4g 50 52 5h 59 60 64 67 693. 3. 33. 3h 35. 36. 37. Assembly being electroformea .- ee eee ee Exploded view of parts stacked for the brazing technique . . Schematic dew of flame furnace see ee ee Connection of 10-foot assembly to support tube . . 5 Furnace showing ring burner in operation... 5. ses Deviation from straightness of accelerator section (brezed). View of finished accelerator section... 1... 54 LIST OF TABLES Frequency dependence of principal machine parameters . . Design parameters of 10 Bev accelerator at 3 frequencies . Comparison of constant-gradient and constant-impedar Sccelerator structures!) se ee Calculated performance of constant gradient accelerator at various values of attenuation parameter tT .. 1... Characteristics of the Stanford constant~impedance structures 6 ee ee Page a ™ B 76 9 33INTRODUCTION A. Historical Review In April, 1957, Stanford University proposed the construction of an electron linear accelerator approximately two miles long designed to pro- duce an electron beam of high intensity in the energy range from 10 to 40 Bev for purposes of particle-physics research. ‘This accelerator was authorized in September, 1961.and is now being constructed on a site on Stanford nd, Stanford is carrying out this work under a prime contract with the U. S. Atomic Energy Comission. The estimated total construction cost of this accelerator is $114 million, and the construction schedule calls for completion by July 1, 1966. The design of the two-mile accelerator ie @ logical extension of the accelerator develoment that began at Stanford University in 1947.2 Up to the present date, the largest of the Stanford accelerators (the 300- foot Mark IIT)® hes operated at energies up to about 1 Bev. The purpose of this report is to discuss the design and fabrication of one of the pr guide which serves as the accelerating structure. neipal components of the two-mile accelerator, the disk-loaded wave- B. General Description Before discussing the detailed design of the accelerating structure it may be helpful to give a brief general description of the two-mile accelerator. A general view of the accelerator and target area is shown in Fig. 1. The accelerator proper will consist of @ disk-Loaded cylindrical vave- guide supplied vith microwave power at a frequency of 2856 Me/sec. The accelerator will be made in sections approximately ten-feet long, and each of these sections will be independently fed with power through a suitable S-band waveguide and vaveguide-to-sccelerator coupler. A total of 960 ten-foot sections will comprise the entire accelerator. The ac- celerator will be supplied with pover by 240 klystron amplifiers, each capable of producing up to 24 megawatts of peak power at 360 pulses per second end 2.5 microseconds pulse length. The pover output from each xlystron will be divided four vays and will be used to supply power to four successive ten-foot sections, as shown in Fig. 2. With this initial 4gil references and footnotes are given at the end of the text, page 80. oeet area. PIG. 1--General view of accelerator and targ19" syaote ree" EARTH | SHIELOI 25° /noss-secri0n / oe wnveGuIo, Rooting ruses Sno MERMAL suncie tee* INSULATION DIRECTIONAL -"N couPLER ~~ a) 2 VALVE FIG. 2 MODULAR ARRANGEMENT OF _KLYSTRON, ACCELERATOR SECTIONS AND ACCELERATOR SECTIONS CONNECTING WAVEGUIDEcomplenent of tubes, each operating et the conservative level of 6 mega- wetts, the aecelerstor will be able to supply an average electron current of 15 microamperes at an energy of 10 Bev. The energy can be increased to 20 Bev and the current to 30 microamperes by increasing the power ouyput fron each Klystron to 24 megawatts. Operation with complement of 2k0 tubes is referred to es Stage I. The accelerator end its related equimment will be situated in two parallel housings, he accelerator proper will be located in an under- ground concrete housing, ll-feet wide and 10-feet high. ‘The klystrons, noduletors, vacuum pumps, end other auxiliary equipment will be located in an above-ground gallery, 30-feet wide and 1 erator housing can be entered only vhen the electron bean is turned of, Dut the Klystron gallery can be continuously occupied. The two housings will be separated by 25 feet of earth which will serve as radiation shieldin, feet high. The accel- There will be @ 3-inch-dianeter transverse pipe between the housings every 20 feet, each containing two waveguide feeds, Under the present authorization, the accelerator will be constructed with a complement of 240 tubes have been made to permit later increase in the number of tubes connected discussed above. However, provisions to the accelerator to a maximut of 960, in which case each Klystron wi feed a single 10-foot accelerator section. This cond: is referred to as Stage IT. With 960 klystrons each producing 24 mega~ watts of peak power, en electron energy of about 40 Bev choulé be obtained. jon of operation II. SELECTION OF CHARACTERISTIC PARAMETERS A. Choice of Operating Frequency Since almost all of the basic accelerator paraneters have frequency dependence, it is first essential to study the implications of using the various frequency bands and to choose en operating frequency. It is not possible to make the choice of frequency by purely analytical methods the final selection requires the application of engineering judgment and reference to previous experience. As 8 guide to the cholee of frequency, the frequency dependence of the principal machine perameters is listed in Table 1. This teble is based upon direct scaling of the modular dimensions of the accelerating -4eTABLE 1 FREQUENCY DEPENDENCE OF PRINCIPAL MACHINE PARAMETERS Frequency Frequency Parameter Dependence notes Shunt impedance per unit length (x) ake x a) RP loss factor (a) pale x | @) Filling tine ( ty} le x (), (2) Total rf peak power suf? x (@), (2), (3) BF feed interval (2) safe x}, @) Number of rf feeds of? x1 Q), (2), HF peak pover per feed re x @). (2), G) RP energy stored in accelerator 2 x @), (2), G) Beam loading (- a¥/ai) 2/2 x 1 (2), (2), (4) Peak beam current at masximun ‘conversion efficiency sue x | (Qs (2)s (3),(6) Diameter of beam aperture et x 1 Maximin rf power available from single source fae x |) Maximun permissible electric field strength af x m Relative frequency and dinensionsl i tolerances ve x (2), (2) Absolute wavelength and dimensional tolerances sole x | @), (2) Poxer dissipation capability of accelerator structure 2 x1), (2), 0) Notes: 1. For direct scaling of modular dimensions of accelerator structure. 2. For same rf attenuation in accelerator eection between feeds. 3. For fixed electron energy and total length. 4, or fixea total length. 5. When limited by cathode emiesion. 6. When limited by bean loading. 7. Approximate; empirical.structure. This astumption has been adopted to simplity the comparison. In @ practical accelerator it is likely that certain compromises would be advisable which would change Tobie 1 in certain details but not in its general inplicetions. The energy of electrons fron a Linear accelerator with negligible vean loading is given by v Kee) 2 (1) wh Py is the total input rf power, L is the total length, r, is the shunt impedance per unit length, and K is a constant ose value depends upon th on, Since r, varies as f*, the rf power required to produce a net rf attenuation in each independently fed accelerator se given final energy in a fixed length is proportional to £7*. Thus con- siderations of pover economy indicate that the operating frequency should be 9s high as possible. Cther adventages of the higher frequencies are the reduced filling time, which varies es £°/?, and reduced eneray storage, which varies es f7®. A shorter filling time is advantageous Since electrons can be accelerated during a larger fraction of the available rf pulse length. the use of the higher frequencies also results in greater maximum field strength (as Limited by breakdown) and larger relative fre- quency and dimensional tolerances. From Table 1 i ean be seen thet the maximo frequency which can be used is limited by the evaileble aperture for the beam end the reduced been-current capability. Another factor against the use of very high frequencies is the increased number of power sources and feeds required. The inereased cost required for the edditional rf systens, modulators, and controls, and the increased operations! difficulties tend to reduce the advantages arising fron the decreased pover consumption at higher frequencies ‘An important consideration not teken into account in Table 2 is the degree of conservatism involved in the choice of frequency band. While Linear electron accelerators have been constructed and operated at L-, S-, and X-bends, the largest anount of experience is available at S-band. In fect, to this date all eccelerats 100 Nev heve operated at S-bend. of this type having energies ab PoeTo illustrate the scaling laws given in Table 1 more specifically, design deta for a 10-Bev accelerator 10,000 feet long are given in Table 2. Tree cases are tabulated corresponding to operating at L-, S-, and X-bands. The specific values in Teble 2 are based on relations and criteria which ere developed later in this section. We shall not coment individually upon each iten in Table 2, but it may be worthwhile to emphasize the following festures. (a) An important espect of the design of the two-mile accelerator is the possibility at some suitable future date of increasing the bean energy fron the initial range of 10 to 20 Bev to the higher range of 20 to NO Bev. For reasons of economy, and to avoid prolonged machine shut- dom, it is desirable to accomplish the energy expansion by increasing the rf pover rether than by increasing the accelerator length. According to Table 2, the L-band structure with a fixed length of 10,000 feet cannot be expanded above about 38.4 Bev without experiencing breakdown difficulties. (>) Te everage rf power requirements ere in the ratio 4.2; 1.0 : 0.4 for the Le, S-, and X-band machines, respectively. (c) The maximum peak beam currents end beam povers are in the ratios of 1.73 : 1,00 : 0.58 for the L-, S-, and X-band machines, respectively. (a) ‘the aperture availeble for the beam in the X-band machine (0.255 in.) is small enough to cause concern about beam transmission, accelerator align- nent, ete. (e) The X-band accelerator ranks highest in terms of maximum expanded energy capability, but the higher energies require X-band sources of higher peak power than ere presently avetlable. For example, operation at 40 Bev would require 4988 sources each producing 2.5 megawatts of peak rf power. (£) Expansion of the L-band accelerator to 40 Bev would require that each of the 185 feed points be eupplied with 200 megawatts of peak pover. This is much higher than the power output obtained from a single L-band source to date and could thus require parallel operation of sources at each feed. {g) Expansion of the S-band machine to 40-Bev would require 22.2 megawatts at each of the 960 feed points. Power outputs above this level have elready been obtained fren single S-band eourees.TABLE 2 DESIGN PARAMETERS OF 10 BEV ACCELERATOR AT 3 FREQUENCIES* Frequency (L-Bana) (S-Bané) (X-Band) 1900 Me/see 3000 Me/sec 9000 Me/aee Shunt impedance pef unit length (r) 0.31 x 108 0.53 x 10® 0.92 x 108 ohms/cm RF loss factor (Q) 2.25 x10 1.3 x10 0.75 x rot Filling tine (t,} Aa 0.83 0.16 usec Total rf peak power 2304 1330 1B BP feed interval 52 10 1.92 tt Number of rf feeds 185 960 ‘4988 RP peak pover per feed 12.5 1.39 0.35 Mw RF energy stored in accelerator 5337 593 66 joules RF energy requirea for 1.67 usec electron beam pulse length 13,778 3385 1405 joules Total average rf power at 360 pulses/see 4.96 0.52 My Beam loading (- av/ai) 20.5 61.5 Bev/anp Peak beam current at maxinun conversion efficiency eT. 157-1 90.7 manne Minimum Aiameter of bean aperture 2.292 0.764 0.255 inch Mex rf peak power available fron single source ak 2.7 Mw Max permissible electric field strength? 333 230 398. kv/em Max expended beam energy 38.4 66.5 115.0 Bev Relative frequency and dimensional. tolerances* Ltd x10 1,93 x 1033.34 x 10S Avsolute frequency and @inensional 11 ke/sec; 58 Ke/secs 30LKe/aecs tolerances’ 0.11 mils 0.06 mils 0.04 mils Average pover dissipated per unit area of accelerator surrace® 0.20 ona 0.18 watts /en? Average temperature difference across accelerator wall® ov 0.03 0.01 degrees ¢ 2n/3 mode in constant gradient structure; t = 0.57 nepers (xf attenuation); L = 10,000 feet (94.8% effective); 10% power loss in waveguides; 10% beam loading; direct scaling of modular dimensions. 1. Assumptions: 2. Based on max gradient obtained to date at S-band; values for other frequencies based on scaling as fl2, 3, As Limited by maximum permissible field strength. 4. For one percent loss in beam energy. 3, Based on’ 360 pulses per second and 1.67 usec electron beam pulse length. 6. Based on copper wall 1/3, 1, and 3 om thick at X-, S-, and L-bands, respectively. .(a) The relative frequency and dimensions) tolerances favor the use of the higher frequencies. Relative tolerances are probably more significant than absolute tolerances, since the former are a better meaoure of the difficulties involved in designing stable frequency sources and in critical machining operetions. (i) Tue average power dissipated per unit area of accelerator surface is not significantly different in the three designs because of the fact that the inereased vall srea at low frequency tends to compensate for the higher power required, and vice versa. However, the average temperature difference aeross the accelerator wall, which is @ measure of the degree of detuning of the structure, is highest at L-band and lowest at X-band. Tt would be possible to compare accelerator designs at the various frequencies in further detail. The designs we have chosen for illustrative purposes Were based upon direct scaling of the modular dimensions of the present S-band accelerstor structure. An improved design at a particular frequency fron the standpoint of over-all economy or perfornance might result from deviating from the sealing lews we have used. For example, the L-band design might be improved by decreasing the feed interval and using @ larger nunber of sources, and by increasing the rf and beam pulse lengths while decreasing the pulse repetition rate. However, this would not affect the totel peak power requirement nor the maximum field-strength capability. Similar alterations might be made at S- and X-bands to improve certain characteristics of these designs. However, ve do not believe that such changes would appreciebly modity the general conclusion we have reached: the S-band accelerator is the optimm choice for the two-mile accelerator for reasons which are implicit in the scaling lave of Table 1 end the itlus- trative examples of Table 2. B. Product of RF Power and Accelerator Length The energy of electrons fron a linear accelerator with negligible ‘vean-loading wes given by Eq. (1). To estimate the power-length product of the two-mile accelerator, we take r= 53 x 10° ohms/meter; moreover, we anticipate the results of Section II.# and use the value, K = 0.82. ‘The minimun objective ds an accelerator which will produce electrons having an energy of 10 Bev under conditions of 10 percent beam loading. ‘The no-load energy must therefore be 11,11 Bev. 1 obtain a realistic -9-estinete, we assune thet 10 percent of the rf pover is dissipated in the rf transmission Lines between the pover sources and the accelerator, and further that 5,2 percent of the accelerator length is used for auxiliary in-line devices and does not contribute to the acceleration process. Substituting the above ascunptions into Bq. (1) ve obtain Pyb = 4.06 x 10% watt om = 1.33 x 107 Mw tt Thus the product of the totel rf power and the accelerator length 7 must be 1.33 x 10" Mw-ft in order to obtain an electron-beam energy of 10 Bey with 10 percent beam loading. C. Selection of Accelerator Length Onee the rf-power accelerator-length product has been determined, these two quantities mict be determinea individually. The following factors influence these selections: 1. Maximm Electrie Gradient As @iscussed in Section 1, the desian objective is @ linear electron accelerator initially capable of producing energies of 10 Bav, with an ultimate capability of 4o Bev energy by addition of rf power without increase of accelerator length. This objective requires that the length of the machine must be chosen so as to permit the maximum ultimate gradient. The maximm average electric gradient obtained in an operating $-vand linear accelerator to date is approximately 4.5 Mev/ft. Using this figure, we find thet a length of epproximetely 10,000 feet is required to satiety the ultimate energy objective. 2. Economie Considerations The totel cost of the accelerator progran may be divided into three partes (#) costs {cp} which are proportions to the totel connected rf powers () costs {0}) which are proportions? to the total accelerator length} and (c) fixed costs (Cel Which include research costs and administrative costs, among others. To be meaningful, these costs must be based on a time period thet includes ~10-the construction time plus @ period judged to represent the useful life of the machine. We have used a period of 10 years useful life in cost studies. From the fact thet rf power and accelerator length have equal weight in the equation for electron energy, it is easy to show that the greatest over-all economy results when C, = Cy. Otherwise, the total cost is given by (2) vere 6 ts the wininn vaine of oy +, [te.) viere Cp (PE pen ¢) Our cost studies have shown that an accelerator length of 10,000 feet is very close to the optimum value to minimize the totel project costs over the 6-year construction period and a 10-year period of operation. 3. Land AvaLlebility There were severe! potential sites available on Stanford land which seemed suitable for the eecelerator project location. An accelerator length of 10,000 feet (plus another 2500 feet, approximately, for research facilities) was possible et most of these sites but no greater length without expensive lend-acquisition costs. Thus the choice of an accelerator length of 10,000 feet satisfies the several conditions discussed sbove, viz., it permite operation at the ultinate expanded energy-gradient; it {s near optimum from the standpoint of over-all economy} and such space is aveileble on Stanford property. ‘Therefore, we have made the selection L = 10,000 feet Which, using the power-length product determined in Sec. IT.B leads to the following initial total connected rf power requirement 1.33 x 107 MwTe should be emphasized that this value of P, is based upon a particcler choice of operating mode (2/3) and upon a particular attenua tion pereneter (+ = 0.57). Their selection is discussed later in this section. The value of P, will vary slightly if another mode or another value of 1 is used. T D. Selection of Number of RF Power Sources and Feed Interval It was established in Sec, II.C that a total rf peak power of 1330 My must be supplied to a 10,000-foot accelerator in order to achieve an electron energy of 10 Bev with 10 percent beam loading. ‘The next logical design decisions are the determination of the number of individual rf power sources and the spacing of the rf feeds elong the accelerator length. In general, it is more economical to obtain a large amount of micro- wave energy from a small number of high-power sources then from a large number of low-power sources. The basic reason for this fact ie that the cost of @ power source depends more strongly on the number and kind of operations involved in its fabrication and processing than upon its physical size and output rating. The cost of employment of the power sources in the accelerator system in terms of auxiliary equipment, instrumentation, controls, waveguide equipment, ete., also decreases as the total number of individuel sources is reduced. Based upon laboratory and commercial experience with high-power klystron amplifiers, it seems reasonable to expect that S-band tubes can be constructed to have an average life of 2000 hours or more while producing ah megawatts of peak rf power and 22 kil- owatts of average rf power. Much higher peak power levels fron single S-band tubes do not appear to be readily obteinable at this time, For reasons of conservatism, it is planned to require initially only 6 mega- watts peak output per klystron, which would result in an electron beam energy of 10 Bey. At this power level, average lifetimes exceeding 2000 hours should be easily achieved. For a totel rf power of 1330 megawatts, 2h0 Klystrons producing 6 megawatts each will be sufficient. Since these tubes will have a design capability of 24 megwattts each, it will be pos- sible to achieve electron energies up to 20 Bev with the initiel complement of tubes. For operation at the Stage II level of 40 Bev, 960 tubes Producing 24 megawatts each will be required. We shall now @iscusss the selection of the feed spacing along the accelereter length. ‘he limiting cases of feed spacing ere (a) a single -12-feed for the entire accelerator, and (b) individual feeds for each of the = 80,000 individual accelerator cavities. The first extreme is obviously infeasible because the full rf power could not be transmitted through the accelerator structure. The second extreme would be prohibitively expensive because of the multiplicity of waveguides and other microwave components and the necessary controls end instrumentation. As deseribed in Section II.K, there is an optimum, or at least a preferred value, of the net rf attenuation between feed points, The choice of attenuation parameter is a compromise among many factors. The attenuation parameter can be adjusted to the desired value by properly choosing the diameter of the aperture in the disk-loaded accelerator structure and the length of the accelerator section. Increasing the aperture size increases the group velocity and decreases the attenuation per unit length. Thus @ given attenuation peraneter can be obteined by either a short accelerator section of high unit attenuation (small aperture), or by @ long section of low unit attenuation (large aperture), or by a com- promise involving medium length and medium aperture. ‘The main factor in favor of close feed-epacing is that the shunt impedance of the accelerator structure inproves slowly as the group velocity is decreased. ‘This is, shown in Figs. 21 and 22. These figures apply specifically to the 2n/3 mode, but the sane general behevior is true for other nodes. Several considerations Limit how closely the feeds should be spaced. These are as follows: (a) Increased costs because of the larger number of componente, controls, waveguides, couplers, rf loads, instruments, ete. (>) tthe complexity of splitting the rf power from each source many times. (c) ‘he decreased aperture available for the electron beam as the group velocity is decreased. (a) Increased operational difficulties because of the increased number of phasing adjustments, monitors, interlocks, etc. In Stage I, 240 rf power sources supplying 6 to ol:megawatts each will be used, as noted above. With equal spscing, these sources will be located at 40-ft intervals along the accelerator length. In Stage II (40 Bev mex), with 960 rf sourees supplying 6 to 2h megawatts power level, it would not be safe (for reasons of rf breakdown) to feed the combined ogpower outputs of 2 or more tubes into an accelerator section. Therefore, at least one feed every 40 feet is required in Stage I and at least one feed every 10 feet in Stage II. However, the shunt impedance is reduced by about 15 percent in going from a 10-foot to a k0-foot feed interval, s0 that the electron energy would be about 7.5 percent less for the sane total rf power input. Noreover, @ very desirable design feature of the machine, as noted in Section I, is the ability to accomplish the transition from Stage I to Stege II operation without a long shut-down period. Such a delay would be required if it were necessery to install additional feeds at the time of the transition. For reasons discussed in the previous paragraph, a feed interval of 10 feet has been chosen fer the two-mile accelerator. This means that during Stage I operation, with 240 rf-power sources, the power output from each feed must be divided 4 ways so as to supply 4 successive accel- erator feeds. To convert to Stage IT operation, with 960 rf sources, the additions] sources can be connected to the already existing feeds with minimum interference to the operations schedule. E, Choice of RF Pulse Length and Repetition Rate For physics-research purposes it 1s generally desirable to have the electron-beam duty cycle (which is defined as the product of pulse repetition rate and beam pulse length) as high as possible. The practical upper Limit of duty cycle is determined by economic considerations. The rf duty cycle mst be greater than the beam duty cycle because a certain time is required to fill the accelerator with rf energy prior to injection of the beam. For the case where the electron beam is injected at a tine after the start of the rf pulse equal to one filling time, the ratio of bean-to-rf duty cycles is given by Sate (9) where t, is the accelerator filling time, and t,, is the rf pulse length. For example, with t, = 0.83 usec (the value for += 0.57 with the 2x/3 mode) and t., = 2.5 usec, the maximm duty eycle ratio as given dy Bq. (3) is 0.67. This may be compared with the value of 0.5 for alethe present one-Bev Stenford Mark III accelerator. An important point. to emphasize is that a given frectional change in rf duty cycle because of increasing rf pulse length permite an even larger fractional increase in the bean duty cycle. ‘Thus increasing the rf pulse length from 2.0 to 2.5 usec, an increase of 25 percent, allows a 43 percent increase in the bean duty cycle (for ty = 0.83 usec). ‘The fectors which place a practical Limit on the maximum rf pulse length are the increasing costs of modulator components, such as the pulse transformers and the pulse-forming networks. on the basis of these considerations, we hove adopted the value of 2.5 micro- seconds for the rf pulse length of the two-mile accelerator. ‘The maximum value of the pulse repetition rate is governed by three prinary fectors: (a) The initial cost of power components increases with increasing pulse repetition rate because of their higher average power ratings. (>) It ts more digficult and expensive to design and construct high-power moduletors at the higher repetition rates. (c) The ac power operational costs for the accelerator power sourees increase almost directly with pulse repetition rate. A msximum repetition rate of 360 pulses per second has been adopted for the tvo-mile accelerator. This may be compared with the maxim rete of 60 pulses per second for the Stanford Mark III accelerator. The com- bination of filling time allows @ maximum beam duty cycle for the two-mile accelerator igher repetition rate, longer rf pulse length, and shorter of sbout .0006, or sbout 10 times greater than that of the Mark TII ac- celerator. 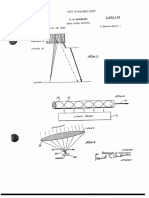F, Selection of Operating Mode ‘The eccelerator structure is 2 disk-loaded cylindrical waveguide of the form shown in Fig. 3(a). ‘The efficiency of the structure as an ac~ celerator of electrons is measured by a quantity called the shunt im- pedance per unit length. This quantity, which we have already introduced in the previous discussion and designated by the symbol r_, may be de~ fined 2 the square of the energy geined (in electron volts) by an electron per unit length for unit rf pover dissipation in this seme length. We heve defined shunt impedance in terms of gain in particle energy to emphasize -15-b) ILLUSTRATION OF DISK DIMENSIONS c) "CONICAL" AND "ANTICONICAL" DISKS FIG, 3--Schematic drawing of disk-loaded waveguide. - 16 -that it is not simply the magnitude of the electric field in the acceler- ator structure which determines the electron energy gain per unit length; rather, it is the amplitude of the Fourier component of the axial field which travels at the electron velocity. ‘The fundamental component is commonly used for acceleration of electrons. ‘The exact value of shunt impedance for a particular configuration of accelerator structure cannot be represented in simple form but can be measured to fair accuracy by microwave techniques. An approximate equation for r, which is suitable for studying the effects of varying the cavity dimensions is Q-n sin D/2\? (4) n+ 2.618, (1 - 0) v/2 where 8, is the phase velocity in the structure divided by ¢, 5 is the skin depth, 4 is the fraction of the length of the structure which is occupied by disks, .e., 1 = t/d = to/A, is the umber of disks per guide wavelength, and is the transit time in radians required for the electron to pess through the cavity gap, i.e., D ~ (2n/n)(1 - n)s Equation (It) cen be derived ty considering an array of simple "pill- box" cavities. ‘This equation gives too high a value of r, for two reasons: (a) the conductivity of the wells is never as high as the idealized value used in calculating the numerical value (968) in the equation; (b) no account is teken of the effect of the disk apertures. Nevertheless, the relative vertation of r, with the spacing and thick- ness of the disks given by Ea. (4) has been confirmed by experimental meacurenents. A graph of r, versus n for f = 2856 Me/sec based on Eq. (4) is shown in Fig. 4 for four values of disk thickness t. Corresponding experimental values obtained from test cavity measurements ere also shown. From Fig. 4 it is possible to draw some general conclusions. For negligible dick thicknesses (t ~ 0), the optimum number of disks per -1T-50. £ = 2856 Me/see 2a = 0.822" for experimental cases (aperture edges rounded) a, = 1.0 © denotes experimental po 3 : 4 al curves of shunt impedance (x) (n) for FIG. ‘+-Theoretical and experine per unit length ve number of disks per wavele various disk thicknesses (t). -18 -wavelength is approximately 3.5. As the disk thickness is increased, the optimum value of n decreases. ‘he best value at t = 0,120 in, is about n= 3. It is about 2.7 for t = 0.230 in., which is the chosen disk thickness. The value n = 3, corresponding to @ phase shift of 2n/2 radi- ans per cavity, hes been adopted for the two-mile accelerator. In addition to the improvenent in shunt impedance, the selection of the 2x/3 node results in fever dicks and improved vacuum conductance compared to the 1/2 mode used with the earlier Stanford accelerators. The basis for the results described sbove may be found upon further examination of Eq. (It). There are three competing factors: (a) The smunt impedance of the individual cavities is improved by increasing the height of the cavities, i.e., the disk spacing. (>) The fraction of the length available for the accelerating fields to act on the electrons is increased as the mumber of disks per wavelength is decreased or as the disk thickness is decreased. (c) As the disk spacing is decreased the electron transit time is decreased correspondingly, and the average or "effective" field strength acting on the electron is increased as (sin D/2)/(D/2). Taus, consider- ations (a) and (b) favor small n and small +, while consideration (c) favors large n and large t. As t dncreases, the fractional space occupied by the disks increases so that r, peaks ata lover value of n. An expression similer to Eq. (I) may be given for the @ of an ac- celerator structure: o 8G - a) x n+ 2.618, (=a) (5) where the symbols have the same meaning as before. A plot of @ versus n is given in Fig. 5. Some measured values of @ are also shown in the seme figure. The quantity Q wes measured in each case by taking two cavity lengths in the ratio of 2:1 in order to cancel out the effect of the end- wall losses. ‘The values of Q are seen to decrease from around 17,000 at n= 2 to about 13,000 at n= 3 and 10,000at n= 4. -19-20,000 18,000 16,000 14,000 \ 12,000 \ oo ' 0.000 in. I 0.061 in. % 10,000 | 0.320 tn. i NN 0.230 in. ' N \ NS 8,000b i \ \ ' 6000+ : | B= 1.0 \ e 1 i 4,000 F \ ' \ \ 2,000 \ I ! \ oL___ 1 td FIG. 5--Theoretical and experimental curves of Q versus number of disks per wavelength (n) for various disk thicknesses (t). - 20-A number of experimental curves for n = 2, 3, and 4 are given in Figs. 6 and 7. The data for these curves were based on disks with un- rounded or "square" boundaries. For a given aperture diameter, rounding of the boundary has the effect of incressing the group velocity and de- creasing the shunt impedence by about 5 to 10 percent. Another observation which is illustrated in Fig. 7 is that the group velocity deereases with Increasing disk thickness at a given value of (except n= 2). This indicates that it my be quite misleading to com- pare the various cases on the basis of the same aperture Giameter (2a). A better comparison would be on the basis of the same value of group velocity, which would thereby insure that the filling times for an accel- erator section of fixed length were equel in ell cases. Alternately, the comparison might be made on the basis of equal values of the product yg which would give equal values of rf attenuation per untt length in all cases. Adjusting 2a to give equal values of v, would reduce r, more severely in the thick-disk cases and vould thus favor the adoption of thin dicks. ‘The limiting factor in reducing disk thickness is the increasing danger of arcing at the disk aperture boundary. G. Constant-Impedance vs Constant-Gradient Structures When an accelerator of uniform modular dimensions (constant impedance) ie fed with rf power at one end, there is an exponential decay of power and electric field strength with exial distance from the input end. ‘This means that the average axial electric field is less than the peak axiel field in the structure, On the other hand, it is possible to design @ structure of non-uniform modular dimensions in which the axial fields will remain constant over the entire length. Such a structure will be referred to as a constant-gradient structure. ‘The ratio of peak-to-average axial electric field strength is unity in the constant-gradient structure, while in the constant-impedance structure it is given by EA cs |. y, (6) l-e oaee cylinder diameter, 2> inches 2a (un-rounded aperture) n, disks per wavelength FIG. 6--Cylinder diameter of disk-Loaded waveguide as a function of loading.0.0. T d= 10.5 cm. 1.0 v,fe 2a = 0.822 in. (un-rounded aperture) t= 0.061 in. 7 t = 0.120 4 t = 0,230 in, 2 3 4 n, disks per wavelength FIG. 7--Group velocity of disk-loaded wave- guide as a fu ion of loading.where 1s the rf attenuation pareneter. [Bquetions (6) through (23) aze given without proce, Tay are derived in reference 3} ‘These ratios are shown vs t in Fig. 8. Thus it is clear that the constant- gradient (c.g.) structure can produce higher electron energies than an optimized constant-impedance (c.i.) structure when both are operating at the breakiown limit of electric-fiela strength. As indicated in Fig. 8 the relative edvantage of the e.g. accelerator in achieving high gradients without breakdown depends upon the value* of 1. Curves of field strength vs axial distance z for the two types of structure are shown in Fig. 9 o.5T. In addition to the advantage of reduced ratio of peak-to-average field strengths, the constant-gradient structure has several other advantages for 1 over the constant-impedanee structure: (a) The power dissipated per unit length in the c.g. accelerator is constant over the entire length of the structure. In contrast, the ratio of power loss st the input end to that at the output end of a constent- impedance structure may be as high as 12.4 to 1. (This magnitude corresponds to « value of the rf attenuation constant + = 1,06 nepers, which gives max- imum no-load energy in the constant-impedance accelerator structure.) This meang thet the tempersture rise in the e.g. structure can be perfectly com- pensated by @ simple frequency adjustment of the rf pover source, thus Preventing phese shift between the electrons snd the wave. Such an adjust~ ment will be imperfect in the ¢.i. structure, thus leading to phase shirt and loss of bean energy. A plot of the power-lote ratios for the tx struetunes is shown in Fig. 10. (e) Te c.g. structure gives a slightly higher no-load bean eneray then the c.i. structure and somewhat lower beam-loading derivative (-aV/di). Thus, the e.g. structure has greater relative energy advantage in the loaded case than in the unloaded case. The no-load energies for the two structures are shown in Fig. 11 and the beam-loading derivatives in Fig. 12. (c) The c.g. structure has a higher maximum conversion efficiency (ratio of maximum electron-veom power to input rf pover) and © higher corresponding maximum peak bean current than the e.i. structure. Curves of the maximum conversion efficiency, aoe and the corresponding maximum beam current, i, _, are shown in Fig. 13. max’ (2) The c.g, accelerator is less frequency-sensitive than the ci. accelerator, 8s show in Fig. 1s. - hev6 constant- impedance etructure: 14 1.0] constant-gradient structure 0.8L 0.6L ogee | L } 1 1 1 1 L 1 4 | ° 0.2 ok 0.6 0.8 1.0 Le t= ot, /2d FIG. 8--Ratios of peak to average axial electric field strengths in constant impedance and constant-gradient accelerator structures versus T. R-TZ, io a CONSTANT IMPEDANCE (Ez=Ege %) 09 08 b o7F 0.6 b AO ole A ale CONSTANT GRADIENT (E, = CONSTANT) 0.3b 02 O1 l i al ! l ! | i ! 9 Ol O02 03 04 05 O06 O7 O8 OF 10 a FIG.9 AXIAL FIELD STRENGTH VERSUS ft FOR EQUAL ELECTRON ENERGY GAIN IN CONSTANT GRADIENT AND CONSTANT IMPEDANCE SECTIONS. T=0.57lo constant- impedance structure —w { constant-gradient str ° 0.2 0.4 0.6 0.8 t= wt, /20 FIG. 10--Ratio of power losses at input and output ends of acceler section for constant-impedance and constant-gradient structures versus 7. = 27 -constant-gradient structure a, 0.8 constant- impedance structure 0.6 vet 0.2 o 0.2 0.4 0.6 0.8 1.0 t= at, /2Q FIG. 11--Unlosded beam energies for constant-impedance and constant-gradient accelerator structures versusconstant- impedance structure constant-gradfent structure FIG. 12--Beam-loading derivatives for constant-impedance and constant-gradient accelerator structures versus 7. = 29 -constant-gradient constant- impedance structure constant. impedance \ structure constant-gradient rueture FIG. 13--Maximum beam conversion efficiencies and corresponding values of peak beam current for constant impedance and constant-gradient accelerators versus 1. 540.8 OTR 0.6L constant- impedance structure o.2- constant-gradient structure 0.2 oO 0.2 Oy 0.6 0.8 1.0 Fe at /2Q FIG. 1b--Frequency sensitivities of uniform and constant-gradient accelerator structures versus t. -31-The advantages discussed above depend upon 1, as shown in Figs. 5-14. To illustrate these factors numerically, the characteristics of the two structures are shown Table 3, vesed upon the peraneters of the tvo- mile accelerator. (c) The c.g, structure is less subject to transient effects than the c.i. structure. Because of the band-pass filter characteristics of an accelerator structure, an impressed rf wave envelope of fin te rise time results in amplitude end phase oscillations’ of the traveling wave. These oseillations recult in a small increase in the width of the energy spectrun of the output electron beam. Experiments et Stanford have shown (Pig. 15) that the trensiens effects are more quick! y damped in the ¢.6. structure then in the ci, structure. (2) Experiments elsewi not troubled by beam "bres! ere® have shown thet the c.g. structure ie 7) paeron- up" (also called "pulse shortenin, ena which ere prevalent with the c.i. structure under heavy beam loading conditions. It eppears that beam interaction does not result in significant excitation of the higher order TM, mode (the radielly deflecting properties of which have been under study® at Stanford since 1959) in the non-uniform e.g. structure as it does in the uniform e.i, structure, Figure 16 shows 8 diegrans for the fundamental 2 10-foot mode st the midpoint “or constant-gradient section and for the TM mode at the input, midpoint, and output. Note thet the v= line intersects each of the higher mode curves at @ different frequency, thus making the build-up of = stro TM,, propageting vave at 2 perticuler frequency unlixely. The advantages of the constant-gradient accelerator discussed above must be weighed against tvo disadvantages: (2) the non-uniform modular dimensions of the cavities in the constant-gradient structure will be more expensive to construct and to test. An economic comparicon of the two structures shows thet fabrication of the c.g. structure will cost approximately 10% more per anit length than the ef. structure. (2) Tere has been relatively little operational experience with ‘the constant-gradient structure compared wiv thet of the uniform structure. We have concluded that the advantages of the c.g. structure given above outweigh the relatively suell cost differential which its use entails. The e.g. structure hes thus been tentatively adopted for ariaTABLE 3 COMPARISON OF CONSTANT-GRADIENT AND CONSTANT- IMPEDANCE ACCELERATOR STRUCTURES Constant- | Constant= Taare Characteristic Pa ee | Sokeaaree | Ratio L [Peak elec. field ao 1,00 az 0.76 Aver. elec. field 2) /2) 5 noo faa ose V, (no-load enerey) air gev [ 11.@ Bey] 2.01 Ber Bey = av/ai 35-53 Sep | 36-4 SS 0.98 Vv (at i= 25 mmps) 10.28 Bev | 10.21 Bev 1.02 fnax bean-conversion 1 i efficiency ) 0.73, 0.70 1.05 os 157-1 ma | 152.3 ma 2.08 normalized 020 +. . 1.68 + 0.5% vale (excap eae at) cadk + .0065 | 0.0121 3 tp (fi2ting time) 0.83 usec | 0.83 usec 1.00 U (stored energy) 593 joules | 593 Joules 1,00 4, p (phase shift for at Pe 1 Ne/sec) 0.52 rad 0.52 red 1,00 BVA, (for BF = 01 Me/sec) 0.033 0.039 0.85 Assumed parameters: t= 0.57 Pip = 1330 Mw (906 of which enters accelerator) L = 10,000 rt (9h.8$ effective) Nunber of sections « 960 £ = 2856 Me/sec ry = 0.53 x 10° ohms/em @ = 13,000 4 -33-triptite FIO.15--Shapes of Snput end outpus rf puloes 2p 8 constant gradient accelerator section (upper ‘arves) and @ constant impedance accelerator section (lover curves). length of section = 10 ft, t = 0.57, and 2x/3 mode in each ease. Rise time of input pulse ~ 0.1 usec; time scale = 0.2 usec/em. -34e4600 44005 4200 ty* 4335.148 ——// 4000 ty? 4246.50 ear eae) 3800 3600}- FREQUENCY (Mc / SEC) 3400! 3200 3000 2800 ° FIG.16- w-B DIAGRAMS FOR THE FUNDAMENTAL TMo, MODE AT THE MIDPOINT OF A 10-FOOT CONSTANT GRADIENT SECTION AND FOR THE TM, MODE AT THE INPUT, MIDPOINT AND OUTPUT. NOTE THAT THE vp=c LINE INTERSECTS EACH OF THE HIGHER MODE CURVES AT A DIFFERENT FREQUENCY. -35-the two-mile accelerator, and high-power tests unter way since the spring of 1962 have confirmed theoretically predicted performance. H. Choice of Attenuation Peremeter ‘The attenuetion perereter ia defined as the net attenuation in nepers in an accelerator section caused solely by resistive wall losses. It is equal to the product of the voltege attenuetion per unit length and the length of the accelerator section. We have designated this product by the symbol t. As stated previously, 1 = wtp/2Q, where w in 2x times the operating frequency, %, is the filling time, and @ is the loss fector in the rf structure. As will be evident in the following dis- cussion, the velue of 1 influences the performance in meny ways, and therefore the proper choice of this parameter js quite important in the lesign of the two-mile accelerator. ‘The totel energy gain V,, in @ constant-gredient accelerator of total T length I and shunt impedence r is given by? 7) where P, is the totel input r€ power, 4 is peak beam current, and r, is the shunt impedence per unit length The first term on the right in Eq. (7) is the no-load enerey (1-© the electron energy et negligible current), and the second term gives ‘the reduction in energy coused by dean loading. The reduction of energy J6 Linear wish Increase in beam current, es shown in Fig. 17. tn plotting these curves it is assumed that the electrons ere situated et the peek of the craveling wave. In the discuseion which follows we shall consider the effect of different values of 1 upon the constant-gredient accelerator performance. ‘The various sccelerator choracteristies ere shown numerically in Table & for these values of 1. 1. Beem-2oading characteristics Beem-loading curves for the various values of 7 under considerstion are shown in Fig. 17. The terminal point on each curve js the heem cur- vent resulting in moximum transfer of rf power to the beem. We note that eecf 2n/3 mode Byq = 1330 Mr (906 effect L = 10,000 ft (94.8% efte: ve) ive) 4 number of sections = 960 f = 2856 Me/see 1 = 0,53 x 108 ohns/neter a 13,000 Oo. 1 1 1 1 1 1 L i ms 1 0 20 ho 60 80 100 120 ho 160) 180 200 i (milliamperes) FIG. 17--Beam-loading curves for constant-gradient accelerator at various values of the attenuationCALCULATED PERF ORMANC! TABLE 4 OF CONSTANT-GRADIENT ACCELERATOR AT VARIOUS VALUES OF ATTENUATION PARAMETER t{nepers) vo | 12 \ a ay (Bev (re) unloaded eneray (Eev} | 12.91 (- aV/ai) beam jonding derivative (Bev/amp) 52.61 | 58.24 fig) energy et 25 ma vean current (Bev) n2.28 | 12.46 (ov), transient energy spread (in Bev) aah} 2.45 ~ O and 25 ma | at max conversion 119.7 ax) efficiency (ma) (OV), energy ices in idle 10-ft section 6.66] 06881} 2.43] 2.30) 24h © et f= 25 ms (Nev) | (vg/e) normalized group velocity* .0252 | .c2ou| can 0160 | .0i52 t Assumptions; =0113. |-+ 10065] 10035] 0082 |-+ oot \ siaiing time (usec) 2 | 0.83] 1.36] 2.5] 3.7% 1 (~ BV/V) energy loss for Bf = 0.1 Me/sec | 0.008) 0033) 0.056] 0.077} 0.098 - ol 2nf3 mode, constant gredient design Pop = 2330 Mw (9C6 of witch enters accelerator) L = 10,000 ft (94.86 effective) Number of sections = 960 f = 2856 Me/sec 0.53 x 208 obns/em @ = 13,000 ‘The group velocity in each 10-ft accelerator section varies linearly between the limits given ix each cclum.the slope (- a¥/ai) of the bean-loading curves decreases in magnitade as 1 decreases. Since electrons with energles from Vp, to Vy emerge fron the accelerator during the transient period, lover values of 1 are preferred to reduce the energy spread. 2. Maximum conversion efficiency The maximuz conversion efficiency of rf power to beam power is given vy? ) Meximin conversion efficiency occurs when the bean current reaches the value” 2 2 role [_ [p-er*]? | a oa 9) eax ep] [he] are | in which case the beam energy is equel to one 3. Energy loss when bean passes through sections not supplied with rf_pover When one of the klystron rf power sources becames defective, it is alf of the no-load energy. desirable to be able to continue operation of the accelerator while the kdystron is being changed. The amount by vhich the electron beam eneray is reduced by exeltation of an idle accelerator section of length 2 is given by? ine eren2t (av), = > [2 - —— Qo) 2 l-e The energy loss decreases as 1 increases, as shown in Table 4. Since ch rf source supplies four accelerator sections during Stage I operation, the totel energy loss given by Bg. (10) must be multiplied by four. This loss is, of course, in addition to the loss of beam energy that would normally be contributed by the four sections (about 40 Mev when the total 39exergy 48 10 Bev). 4, Group velocity In the constant-gradsent accelerator, the group velocity decreases Linesrly with distance along the accelerator section. It is given by? of [1 - (2/2)(2 - e787) Bo rer (2) 5. Filling time A small filling time is desirable to allow the maximum available por- tion of the rf pulse length for the acceleration of electrons. The filling time is given by? (ae) Values of filling time for the various cases are given in Table 4. 6. Frequency sensitivity The frectionel beam-energy loss fron a fractional frequency shift bs/t 4s given by (13) Values of Bv,¥, ere shown in Table 4 for 8f = 0.1 Ne/see. 7. Conetusions From Table 4 it ds clear that there are several advantages to using a reduced attenuation paraneter t. Except for the reduction in beas energy, the general statement can be made that the use of a low value of 1 results in improvenent of all of the factors measuring the per~ fomance of the accelerator, Moreover, the percentage improvenent of each of these factors resulting from a given reduction in t usually exceeds the percentage lose in bean energy. If it were not for the para- mount importence of high bean energy in particle-physics researen, the - ko -adoption of @ very low velue of + would clearly be indicated, It has not seened reasonable to us to make the selection on a strict analytical basis. We have instead made the choice of on the basis of brosd con- siderations, including reference to such tabulations as shom in Teble 4, prospective requirements of physics research, and previous accelerator experience. We have chosen the value? of 1 = 0.57 for the sections of ‘the two-mile acceleratTTI, EMPIRICAL DESIGN OF THE ACCELERATOR STRUCTURE A. Choice of the Disk-Loaded Waveguide The previous sections of this paper feve been concerned with the general determination of accelerator parameters. This section deseribes the pro- cedures used to design empirically an accelerator structure that satisfies the sbove parameters. The ats “loaded waveguide is not the only slow-wave structure capable of accelerating electrons. In fact, other structures (see Fig. 18) such as the grid-loaded waveguide yield shunt impedances about twice that of the disk-loaded guide. But in every case ve have examined where a lerge improvement in shunt impedance (r) has been obtained, the bandwidth and iting group velocity are at least ten times as high as desired. Efficient utilization of the available rf power under these conditions would have required its recirculation (feedback) or the use of extrene lengths between feeds, The fomer is undesirable, especially in a long multi-section accelerator, since it results in undue operational compli- cations; the latter requires thet each accelerator section trensmit an excessive amount of power. Several varietions of structures 2-8 chown in Fig. 18 were devised which succeeded in reducing the group velocity to the desired values (in the range of 0.01 c), but these measures also caused the shunt impedence to be reduced until no advantage remained; moreover, they resulteg in ineressed cost of fabrication. For these reasons, the disk-loaded waveguide appears preferable for the twoumlle ac- celerator to ell other structures examined to date. finition and Discussion of Dimensions The moduler dimensions of the disk-loaded waveguide which can be ea- Justed to achieve the intended parameters ere illustrated in Fig. 3. Fig- ure 3(a) shows the cylindrical guide dioneter 2b, the disk-hole disneter 2a, the disk-edge radius , and the land in the disk aperture s. Fig- ure 3(c) shows further varietions of the disk-loaded weveguide using so- called "conical" or "anti-conical" disks. The conical disk was rejected Decause of its comparatively low r/Q. The enti-conical disk was also omisced; although it has a five percent higher r/@ than the corresponding flat disk structure with t = t, = 0.230 in., this value is still five - he