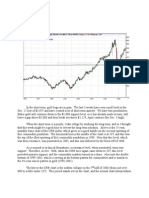
, November 21, 2003) Black Monday Drawdowns represent unusually large single-day negative returns in the stock

market. While this alone is a significant deviation from average stock returns, even more important is the fact that
before October 19, the market had already declined three days. Market losses were 2%, 3% and 6% over the previous
three trading days. In other words, there were four consecutive losing trading days, causing the market to drop 30%.
These periods of consecutive losses are called declines. Sornette has been studying these types of impairments in an
attempt to understand why exceptions occur and how they can be built into RWH. He argued that although
independence could correct a large deviation, the probability of two or more large deviations occurring in succession
was stratospheric. For example, the probability of the stock market falling 10% in a day is about 1 in 1,000. In other
words, a 10% decrease would statistically occur every four years. Although a drop of this magnitude would be a large
deviation from the average daily stock return, it would fall within a normal distribution. If stock returns were
independent, then the probability of two consecutive daily declines of 10% would be the product of the probability of
the two independent events, or 1/1000 multiplied by 1/1000. Similarly, the probability of three consecutive 10%
declines or 30% declines is 1/1000 × 1/1000 × 1/1000, or 1 in 1,000,000,000. This means that, statistically, a 30%
drop in three days can only happen once every four million years! Of course, historically, these sequential events have
occurred, especially when the market declines. Eliminating randomness in such events suggests that when sequential
returns reach a critical level. is no longer random or independent. Sornette calls these periods “dependency
explosions” or “predictability.” If these successive declines occur more frequently than what would be statistically
predicted, then some correlation between daily stock returns must exist, suggesting that stock returns do not follow a
single step. go randomly. TABLE 4.2 Historical Declines of the Dow Jones Industrial Average* Dow Jones Ranking
Start Date Time (Days) Decline (Percent) 1 October 1987 2508 4 –30.7 2 July 1914 76.7 2 –28.8 3 October 1929 301
3 –23.6 4 July 1933 109 4 –18.6 5 March 1932 77.2 8 –18.5 6 November 1929 238 4 –16.6 7 11/ 1929 274 2 –16.6 8
August 1932 67.5 1 –14.8 9 December 1931 90.1 7 – 14.3 10 September 1932 76.6 3 –13.9 11 September 1974 674
11 –13.3 12 June 1930 240 4 –12.9 13 September 1931 110 5 –12.4 14 August 1998 8603 4 –12.4 *Adapted from
Didier Sornette, 2003 As shown in Table 4.2, Sornette's research indicates that large declines in the DJIA have
occurred frequently more frequently than statistically expected. Looking at the three biggest stock market downturns of
the 20th century (1914, 1929, and 1987), Sornette calculates that statistically, about 50 centuries separate downturns
of this magnitude . He concludes that three declines of this magnitude occurring three-quarters of a century apart are
a sign that the series of returns are not completely random. What Sornette discovered is that under normal
circumstances, profits follow a normal distribution. These normal conditions represent about 99% of the market
decline. However, there appears to be a completely different dynamic occurring in the remaining 1% of withdrawals;
These declines occur at the tail end of the distribution when the market declines abnormally (see Figure 4.3).
Interestingly, Sornette also noticed declines, this outlier behavior is common for currencies, gold, foreign stock
markets and stocks of large corporations, although the day-to-day declines were in the normal distribution. 38 Part I
Introduction Download at,In this chart, Sornette compares the number of specific withdrawals vs.