Quantum computational chemistry[edit]

Main articles: Quantum chemistry, Electronic structure, and Quantum computing

Quantum computational chemistry is an emerging field that integrates quantum mechanics with
computational methods to simulate chemical systems. Despite quantum mechanics' foundational
role in understanding chemical behaviors, traditional computational approaches face significant
challenges, largely due to the complexity and computational intensity of quantum mechanical
equations. This complexity arises from the exponential growth of a quantum system's wave function
with each added particle, making exact simulations on classical computers inefficient. [56]

Efficient quantum algorithms for chemistry problems are expected to have run-times and resource
requirements that scale polynomially with system size and desired accuracy. Experimental efforts
have validated proof-of-principle chemistry calculations, though currently limited to small systems. [56]

Historical context for classical computational challenges in

quantum mechanics[edit]
 1929: Dirac noted the inherent complexity of quantum mechanical equations, underscoring the
difficulties in solving these equations using classical computation.[57]
 1982: Feynman proposed using quantum hardware for simulations, addressing the inefficiency
of classical computers in simulating quantum systems.[58]
Methods in quantum complexity[edit]
Qubitization[edit]
Main article: Unitary transformation (quantum mechanics)
One of the problems with hamiltonian simulation is the computational complexity inherent to its
formation. Qubitization is a mathematical and algorithmic concept in quantum computing to the
simulation of quantum systems via Hamiltonian dynamics. The core idea of qubitization is to encode
the problem of Hamiltonian simulation in a way that is more efficiently processable by quantum
algorithms.[59]

Qubitization involves a transformation of the Hamiltonian operator, a central object in quantum

mechanics representing the total energy of a system. In classical computational terms, a
Hamiltonian can be thought of as a matrix describing the energy interactions within a quantum
system. The goal of qubitization is to embed this Hamiltonian into a larger, unitary operator, which is
a type of operator in quantum mechanics that preserves the norm of vectors upon which it acts. This
embedding is crucial for enabling the Hamiltonian's dynamics to be simulated on a quantum
computer.[59]

Mathematically, the process of qubitization constructs a unitary operator such that a

specific projection of proportional to the Hamiltonian H of interest. This relationship can

often be represented as , where is a specific quantum state and is its

conjugate transpose. The efficiency of this method comes from the fact that the unitary operator
 can be implemented on a quantum computer with fewer resources (like qubits and

quantum gates) than would be required for directly simulating [59]

A key feature of qubitization is in simulating Hamiltonian dynamics with high precision while reducing
the quantum resource overhead. This efficiency is especially beneficial in quantum algorithms where
the simulation of complex quantum systems is necessary, such as in quantum chemistry and
materials science simulations. Qubitization also develops quantum algorithms for solving certain
types of problems more efficiently than classical algorithms. For instance, it has implications for the
Quantum Phase Estimation algorithm, which is fundamental in various quantum computing
applications, including factoring and solving linear systems of equations.[59]

Applications of qubization in chemistry[edit]

Gaussian orbital basis sets[edit]

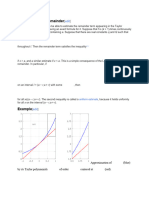
In Gaussian orbital basis sets, phase estimation algorithms have been optimized empirically from

to where is the number of basis sets. Advanced Hamiltonian simulation

algorithms have further reduced the scaling, with the introduction of techniques like Taylor series
methods and qubitization, providing more efficient algorithms with reduced computational
requirements.[60]

Plane wave basis sets[edit]

Plane wave basis sets, suitable for periodic systems, have also seen advancements in algorithm
efficiency, with improvements in product formula-based approaches and Taylor series methods. [59]

Quantum phase estimation in chemistry[edit]

See also: Quantum fourier transform and Quantum phase estimation algorithm
Overview[edit]

Phase estimation, as proposed by Kitaev in 1996, identifies the lowest energy eigenstate (

) and excited states ( ) of a physical Hamiltonian, as detailed by Abrams and Lloyd in 1999.
[61]
In quantum computational chemistry, this technique is employed to encode fermionic
Hamiltonians into a qubit framework.[62]

Brief methodology