AP Calculus AB Review Transcendentals, Diff Eqs., Area/Volume = Name: Answee key Determine the derivative of the following functions. 1) = Ing 8) 2) 0) [ee \ 3) state | secle™) Oa 4) Sogn (Ode fore - / nyo hel a fiat )— (fn) a 4 } [Tepey | - : | Evaluate the following integrals. seeks, Ps hax we Inx Po = 5x Tere ucleok OI ede a ol teu Ligy daz seed ee du ada Ska st BSC Lyd [ae « falul ac sale ae “c —— Paldnrlre Pic] [Selte*e] ae [ae 10), dx ye [ee" Wied ol we A ftan(4x)dz yo ¥ i du e"de ieee ducetar Mtns) dur ude Sear oe Eten “Lay pnlul®© { x [nlite [rc |13) Consider the differential equation 2 = — 2, ” ‘ ‘ {2} On the axes provided, sketch a slope field forthe given differential equation at the twelve points indicated. , ‘ ‘ ’ as {b) Let y= fx) be the particular solution tothe differential equation with the initial condition f(2) =-2. Write an ‘equation for the lie tangent tothe graph of fat (1, -1) and use it to approximate fi.1) Be lu - O. 2 ee ge hoe yr ael yd (91s the approximation for F2.4) found in part (b) an underestimate or overestimate? Justty your reasoning. 4 ) Clea Ca Day Beta. SVG. ts fe greth % concart wf, £0 Mell) is an underestimate. (6) Find the particular solution y = fix) tothe given differential equation with te inital condition f(t) =-3. 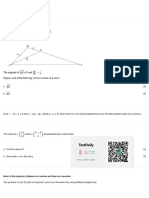Syayef Ixdx14) Find the particular solution y= fx) to the differential equation © = x?(y — 1) with the initial condition foi aye de 7 ca \e me yl Je ret ae | yt ce” pee 3tece 2 Ce BC 15) Letfand g be the functions given by (x)= + sin(rx) and glx) = 4~*, Let be the shaded region in the ‘st quadrant enclosed bythe -ans and the graphs off ang, and lets be the shaded region inthe first ‘quadrant enclosed by the graphs off and g, as shown inthe figure below. 0) Find the area of R. maid Se ~ (4 sats) dx (0) Find the ara of, 3) fe Geese) vt wpa c) Find the volume of the solid generated when S is revolved about the horizontal line y = -1. 1 a Cla-t o Ny Veoh (teenie = nf O™st)dn ae ree16) Let Re the shaded region bounded bythe graphs of y = VF and y = e* and the vertical wees S shown inthe figure below. ; (2) Find the area of. “ Az SiR - e”)as D304 [rae] {b) Find the volume ofthe solid generated when R is revolved about the horizontal line y = 1. Ve nf (eee = af (1a ans furs (ERR {) The region Ris the base ofa solid. For ths sold, each ross section perpendicular to the x-ans is 2 rectangle whose height is 5 times the length ofits base in region R. Find the volume of this solid, Ve § (r= 2") (5407 -€"))de volume ofa sphere with radius is V = Snr? {a) At the time when the radius of the sphere is 10 centimeters, what isthe rate of increase ofits volume? Hobe Ie eoslows ads [4 BY mete at (b) At the time when the volume of the sphere is 36m cubic centimeters, what is the rate of increase of the. area of across section rough the center fhe loxem/s vere (A> ne”, ; a, Ax (3)(0.04) 3M ca ho em) Somes Bee ynee (aR, aye O°%] gee La ae