Scribd Logo
Upload

Welcome to Scribd!

  • Handout 1

    Uploaded by

    Han ho
    20 views10 pages

    Original Title

    Handout1

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document

    Copyright:

    © All Rights Reserved
    Download as PDF or read online from Scribd
    Flag for inappropriate content
    20 views10 pages

    Handout 1

    Uploaded by

    Han ho

    Copyright:

    © All Rights Reserved
    Download as PDF or read online from Scribd
    Flag for inappropriate content
    of 10
    Howdout #4 ELEC 383 I. General Characteristics of Biomedical Signals Before designing any instrumentation system, an engineer must have a thorough understanding of the nature of the signal that he wishes to measure. This is especially true in the design of medical instruments, because of the unique characteristics of biomedical signals, What makes biomedical signals unique? What distinguishes blomedicai signals from those that an engineer would deal with in the design of a voltmeter or a compact disk player, for example? In this handout we will see that biomedical signals have a number of features that demand the attention of designers of biomedical instrumentation. Figure 1 shows four common signals obtained from the human body. Three are related to the sounds and movements of the heart and one is related to the electrical activity of the brain. It is not important for you at this early stage In your studies to know the deralls of how the signals were transduced. 1 simply want to direct your attention to some of their general © AWW «HHH Figure 1. Examples of common biomedical signals. (a) pulse, (b)electrocardiogram (ECG), (c) electoenencephalogram (EC), First, we should note that these waveforms only represent a snapshot or sample of a much longer time record, If we were to look at recordings made a few seconds later, it is likely that the signals would not appear much s. The higher the input Although this energy shunting effect plays a role in the measurement of some bioelectrical and biomechanical signals, a much more subtle and important effect that must be dealt with frequently when measuring signals derived from the human body is Its reaction to any intrusion that is perceived as harmful or potentially harmful. This can be elther a psychological or an involuntary physiological reaction. Let's take an example. Suppose that a student decides that he wants to measure the temperature of the skin with # digital thermometer that he just finished building as part of his final-year project. The thermometer is an automated, microprocessor-controlled instrument with a 4-digit LCD isplay.. Its probe te designed to clip of the ear and it can record the time profile of the temperature in real time with great accuracy (he thinks), He stuffs the thermometer in his knapsack and walks back to the dormitory to try it on one of his friends. It's February and the air is cool outside. $0 by the time the student arrives at the dormitory the temperature of the metallic probe of the thermometer is considerably colder than that of the skin. Because he is quite excited about demonstrating his device, he does ot pay mucn attention to this fact. within minutes after the stuclent arrives, his friend has already agreed to help him with his little experiment. The student places the temperature probe on his friend's Gav and begins recording. When the temperature appears to stabilize, a he stops recording and prints out the temperature record, This is what he measures: wo a © 19 26 go time (5) The student thinks that i's quite strange that the temperature stabilized at such a low temperature-only 20 °C. After al, isn't the body temperature about 37 CP He decides to try again and clips the probe back on the ear in the same piace. ‘This time, this is what he measures: are. BN ast ee eee ow ae ae tee (5) ‘Now he is thoroughly confused. Why did the temperature go up and then ack down again, and then finally appear to stabilize at a higher temperature than ie did last time?” Maybe his thermometer is not as accurate ashe thought afterall. iste ‘There is po problem with the accuracy of the thermometer, ‘The problem lies in. the influence of the temperature of the probe on the response of the skin. The skin is not simply'a chunk of material with a certain thermal mass that heats or cools according to a first-order model of thermal conduction. It contains its own’ temperature-regulation system that attempts to adjust the local blood Flow in a way that satisfies the local metabolic needs of the tissue, while at the same time maintaining the core Body temperature at a constant value. One must understand the subtleties of how an external thermal stimulus affects the state of this feedback system if one wishes to know the "true" temperature of the skin. ‘There are many other examples of similar effects caused by measurement devices on living systems. A rule of thumb for minimizing these effects Is to design a biomedical instrument to be as non-invasive as possible, Regardless of whether an external stimulus is applied purposely (as 1s the ‘case in medical imaging devices that employ a form of electromagnetic radiation) or unintentionally as in the temperature-measurement example above, care must be taken to reduce the physiological disturbance eaused by the instrument as much as possible. Clearly, the extreme case of causing physical damage in the course of making a measurement Js of foremost ‘concern and should be avoided at all costs. This requirement for non-invasiveness often means that the true characteristics of 2 biomedical signal must be inferred from indirect ‘measurements, a task that Is Frequently referred (o as remote sensing. ‘The information content of the signals acquired by remote sensing is, in general, lower that that of directly measured signals. Let's suppose, for example, that we wish to measure the electrical activity af 2 single neuron located deep in the brain, as illustrated In Figure 2. No method now exists for accomplishing this'in a totally non-invasive way. To make this ‘measurement with currently available instrumentation, 2 part of the skull must De removed so that an electrode can be pushed through the brain, 3 until its tip lies close enough to the neuron. Naturally, this direct methc not the method of choice under most conditions. As an alternative, could try to measure the electrical signals produced by the neuron witl electrode placed on the surface of the scalp. But an electrode placed sc away from the neuron would sense only a tiny fraction of the elect: current generated by the ncuron. Also, this weak signal would be m: with those produced by many other neurons and would most probabl: overwhelmed by signals from neurons located closer to the electrode further measurement difficulty would result from any signal distor introduced during propagation through the brain tissue between neuron of interest and the electrode. This example illustrates some of challenges involved in the measurement of biomedical signals by ren sensing. sther ‘og \Gledrode ters a. skull neuren Bran Figure 2. An example of a remote sensing problem. It is important to realize that even if we could somehow eliminate all of noise introduced in the process of measuring a biomedical signal Inherent biological variability in the characteristics of a biological sij measured from different individuals would remain. This variabilit usually considerably larger than that to which many engineers who i with clectronic systems are accustomed. For example, most engin’ would consider a variation of + 5% in the magnitude of the output vol! of a computer power supply manufactured in separate batches to be nor and within acceptable tolerances, whereas a physician may consid difference as great as + 25% between the heart rates of two patients t in the normal range. The large--and often unknown-statistical varia’ of signals measured from different individuals makes the identificatio: an ideal or "prototype" signal for the specifying the accuracy or signal noise ratio of a measurement system difficult; consequently, one is o: forced to specify a prototype signal as an average measured in a cer population of subjects. Let's pause here to summarize the characteristics of biomedical signals we have discovered thusfar in our discussion, 1. Biomedical signals can be treated as tandom_signals with a sandom noise component. Their unpredictability results from inherent biological variations and environmental influences. 2. They are susceptible to disturbances related to the measurement process. Such disturbances can result from normal physiological or psychological reactions, energy shunting, and physical damage. 3. Remote sensing, rather than direct measurement of biomedical signals is often necessary. Signal acquired by remote sensing are, in general, highly attenuated, blurred. and intermingled. Although this list could be made longer, I think it would be more productive to move on to the task of describing the characteristics of biomedical signals in a more quantitative way. This is the objective of the next section. II. Mathematical Description of Biomedical Signals To facilitate our study of biomedical instrumentation, we need a common language for describing biomedical signals quantitatively. This section, outlines a mathematical framework for this language based on random signal theory. As discussed in Section J, most biomedical signals behave in a non-deterministic manner, so it is natural that we shall rely on ‘mathematical functions that are suitable for describing their statistical properties, You are probably already familiar with most of the definitions and concepts presented here from your earlier studies, but if you do not feel comfortable with any topic and would like to refresh your memory, 1 recommend that you refer one of the following textbooks: Probability Methods of Signal and System Analysis, G.R. Cooper and C.D. McGillem; Probability and Stochastic Processes for Engineers, C.W. Helstrom; or Probability, Random Variables, and Schochastic Processes, Papoulis, A. 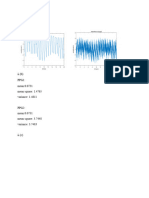Consider the signals 5,(0)53(0).5,( shown In Figure 3, which represent a set or ensemble of samples of a generalized time-varying random signal ‘S(. By writing S(t), 1 do not mean to imply that the signal is only a function of time; it could Just as well be written as S(,,...) to indicate that it is also a function of location and other variables. However, for simplicity, let's treat it as a function of time which fs influenced by other unspecified or unknown variables. so Figure 3. A set (ensemble) of samples of a random signal S(t) showing its behavior within different time intervals. 5 ‘There are several approaches to the quantitative description of S(t). We could try to fit by an equation made up of elementary functions like r", sin), or exp(). But it is clear from the differences in the shapes of 5,(1.Sp(0,--.5_(0) that S(Q) does not have a fixed or periodic shape and, therefore, any such equation would be an accurate predictor only within a short time interval. Fortunately, for the applications with which we are concerned, the essential features S(¢) can be described by a few well- chosen statistical quantities: 1, Mean, mean-square, and peak-to-peak (p-p) values 2: Probability density function 3. Autocorrelation function 4, Power spectral density These quantities are defined in the following paragraphs under separate headings. A. Mean, mean-square, and p-p values. In a discretely sampled random process, the mean (also called the “expected value") is found by simply summing the sampled values and dividing by the number of samples, In an analogous way, the mean of S(t) , a continuous random signal can be written as i’ a SH- stim + fsuyar Eq.(1 te 7h where T is the measurement period. The mean is the most important measure when the information contained in the fluctuation of S(r) are regarded as noise. Often, however, the fluctuation in a signal generated by a biological process is the primary carrier of information. In these cases, the mean-square value and variance of S(t) are useful descriptors. The ‘mean-square value of S(t) is a measure of the average power of the signal, S@Q= 1 Te im — [S2(0) de 1 Eq.(2) Foe Tg which is closely related to its variance, %, J oF tim = f[sy-Sofa 9.3) A T= Tg Note from Eqs. (2) and (3) that_o? = 5%(f) when S()= 0, ie., the mean- square value and variance of S(t) are equal when it has no DC component. The square roots of S(t) and 0? are referred to as the root-mean-square (RMS) value and standard deviation, respectively. ‘The average peak-to-peak value of S(t) is simply the difference between its minimum and maximum values averaged over a time interval T, eee pp = im. S[Snax(~ Saint] Eq(4) This is a useful quantity for describing the envelope of a signal modulated by another signal or by noise. For example, the peak-to-peak value of the blood pressure, specified as the difference between the systolic and diastolic variations of the blood pressure during the cardiac cycle is an important indicator of the resistance to blood flaw in different parts of the body. B. Probability density function. The probability density function f(x) specifies the probability that a sample X = S(r,) taken at an arbitrary time ¢, lies within a range of values between x and x+dr, Fla) de=Pr (xX

    You might also like