Chapter | KY RATIO AND PROPORTION WW ak at COR Read Ratio + Proportion + Unitary Method In our daily life, many a times the! For example Sam's height is 150cm and height of his younger brother John is 75cm We can say that, Sam is 75cm taller than John or John is 75cm shorter than Sam. We call such a comparison as comparison by difference. We can also say that Sam is twice or two times as tall as his brother John because Sam's height 150 John'sheght 75 7 This is called comparison by division or simply “ratio” In other words, a ratio is a comparison of two numbers or quantities by division In general a ratio compares the two quantities in terms of "how many times one quantity sto other fa and b are two quantities of the same type and in same units, then the fraction > is called the rato of atob. b Itis denoted as “a:b” and is read as “a is to b”. The quantities a and b are called the terms of the ratio. ais known as antecedent and b is known as consequent re is a need to compare two quantities of the same type Thus we can say that Sam’s height: John’s height = 2:1.» Since ratio is a fraction, we can Bet equivalent ratios by multiplyin, and denominator by the same number. een cote (2x2) 23=he sare" 46> 2:3 = 4:6 2030 = 39 = 20410. 2. 23> 20:30-2:3 » Usually ratios are expressed in their simplest or lowest terms. » The order of terms in a ratio is very important 4:3 is different from 3:4, We can easily verify that * ? » As every ratio can be expressed as a fraction, therefor them to fractions, Example 1: There are 20 boys and 15 girls in a class. (a) What is the ratio of number of boys to number of girls? (b) What is the ratio of number of girls to number of boys? (c) What is the ratio of number of boys to the total number of students in the class? re we can compare the ratios by converting Solution: No, of boys = 20 No. of girls = 15. (a) Ratio of number of boys to number of girls =22=4= 4:3 (b) Ratio of numberof girs to number of boys =25-= 3 «34 {c) Total number of students = 20 + 15 = 35 PABA Ratio of number of boys to total number of students = 39 == 4:7 Example 2: Find the ratio of each of the following in the simplest form. (a) 30 minutes to 2 hours (b) 40cm to 2.5m (c) 75 Paise to%2 (d) 1 litres to 250m! ={b) 1m = 100 cm, so 2.5m = 2.5 x 100 = 250 cm 240 = 4, Ratio of 40cm to 2.5m 350 550" 4:25 (c) & 1 = 100 paise , so ® 2 = 200 paise =2= Ratio of 75 paise to® 2= 25.= Zor 38 (d) 10 = 1000m/ Ratio of 1 litre to 250m! = 1000 = 4 or 4:1 Example 3: Out of 50 students in a class, 25 opted for cricket, 15 opted for table tennis and the remaining opted for basket ball. if a student can opt for only one game, find the ratio of {a) Number of students who opted for cricket to number of students who opted for table tennis (b) Number of students who play table tennis to number of students playing basketball {c) Number of students who opted for basketball to total number of students Solution: Total number of students = 50 Number of students who opted for cricket = 25 Number of students who opted for table tennis = 15 Number of students who opted for basketball = 50 - 40 =10 (a) Ratio of number of students who opted for cricket to number of students who opted for table tennis =23=3or 5:3 (b) Ratio of number of students who opted for table tennis to number of students who opted for basketball =43 = Zor 3.2 (c) Ratio of number of students who opted for basketball to total number of students =. or 1:5 Example 4: Which is greater 2:5 or 5:3? Solution: We know 2:5 = Band 5:3 =3 Now we will compare2 and LCM of 5 and 3 is 15. be ie ee 5:3 >25 John’s home to the distance of the school from Mary's home 's 2:1a a {i) Who lives nearer to the school? {i) Complete the following table which shows some possible distances that John and Mary could live from the school. {ili) if the distance of John’s home to distance of Sam’s home from school is 1. 2, then who lives nearer to school? Solution: {i) (distance of the school from John’s home) 2 {distance of the school from Mary’s home) } > distance of the school from John’s home = 2 (distance of the school from Mary’s home) s+ Mary lives nearer to the school {ii) Completing the table by writing equivalent ratios, the completed table is as follows: ii) (distance of the school from John’s home) _4 (distance of the school from Sam's home) 2 Then,distance of the school from Sam’s home = 2( distance of the school from John’s home) ~. John lives nearer to the school Lets now try to divide a quantity in given ratio. Example 6: Divide % 600 in the ratio 1:2 between Rohan and Sohan. Solution: Here, the two terms of the ratio 1:2 are 1 and 2. +. Sum of the parts= 1+2=3 Ifthe money is divided into 3 equal parts then Rohan’s share is 3.of € 600 = x600 = %200 ‘And Sohan’s share =2 of & 600 =2 x600 = ¢ 400. (b) 24cm to 5 m (c) 75 paise to % 3 (e) 25kg to 250gm —_(f) 500m to 2 km3. Compare the following ratios. 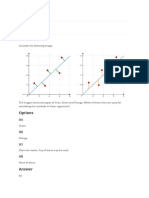(a) 5:7 and 7:5 (b) 12 :36 and 15:45 (c) 3:5 and 7:30 § Look at the figures given below and find the ratio of the following porta (a) Number of triangles to number of circles. (b) Number of rectangles to number of triangles. (c) Number of squares to number of circles. (d) Number of rectangles to number of squares. (e) Number of circles to total number of the figures. }. Ina town of population 25,000; 10500 are males, 9500 are females and remaining are children Find the ratio of » (a) Number of males to the total population of the town. (b) Number of females to number of males. {c) Number of children to the number of males. (d) Number of children to the number of females. i. Inayear Rahul earns % 2,00,000 and saves ® 50,000.Find the ratio of : {a) his income to his expenditure _(b) his savings to his income '. The cost of a dozen bananas is ¥ 60 and cost of 4 oranges is @ 24, Find the ratio of cost of a banana to the cost of an orange. |. Distances travelled by John and Tom in 2 hours are 40 km and 50 km respectively. Find the ratio of speed of John to the speed of Tom. Out of 40 students in a class, 12 opted for Sanskrit, 15 opted for German, 8 opted for French and rest for Spanish, Find the ratio of : (a) Number of students who opted French to Spanish. (b) Number of students who opted Sanskrit to German. (c) Number of students who opted German to total number of students. Divide 110 between Amit and Arpit in the ratio of 3: 2.11. Ramesh wants to divide 14 presents between his sons Daksh and Daman in the ratio of the marks obtained by them in their unit tests. if Daksh scored 20 marks and Daman scored 15, find how | many presents will each of them get? | 12, Ashaand Usha decided to divide their annual profit inthe ratio 3 5. the annual Profit was | %3,20,000. Find their respective shares | However, Asha had a change of mind and decided to divide the profits equally Who was | benefited from this decision and by what amount? | 13. The distance between two cities on a map is 7 cm. If the map has a scale of 1.300 what is the | actual distance between two cities? 14. The ratio or the sides of a scalene triangle is 2 : 3 : 4. The perimeter of the triangle is 63 cm. Find the sides of the triangle. 415. Sonia divided her money in the ratio 5:2 between her son and daughter. If son got & 155, find her daughter's share. 16, Ratio of speed of train A to speed of train B is 2:1. | {a) Which train moves faster? (b) Complete the following table which shows some possible speeds of both the trains in km/hr the ratio of speed of train A to speed of train 6 is 1:2, then which train is moving slow? (ON ook at the following situation. went to the market to purchase oranges. Shop A was selling Skg oranges for € 510 and shop ‘was selling 2kg oranges for 204. Which shop was selling the oranges at cheaper rate? Can you think of a way to solve the above problem? ‘We can use the concept of ratios to arrive at a solution. Let's find the ratio of the weights Skg: 2kg = 5:2. The ratio of the costs is € 510: 8 204 = $40 = 35:2 ‘As both the ratios are same, thus both the shops are selling oranges at the same rate. We can also say that 510:204= 5:2 Or ratio of weights of oranges = ratio of the costs of oranges. ‘Since both the ratios are equal , hence we say they are in a proportion. If two ratios are equal, we say that they are in proportion and use the symbol ‘or the two ratios. __#+510;204= 5:2 can also be written as 510:204; 5:2 wm. to equate‘In general, if four numbers say, a, b, c and d are such that a: b = c: d, then a b, c and d are said to be in i proportion. The symbol :: is used for proportionality. Ina statement of proportion, the first and fourth terms are known as extreme terms. The second and third terms are known as means terms. asrob e. 4 And a:bzzerd is read as ‘aistob as cis tod’. If ad # be, then a,b,c,d are not in proportion. if out of a,b,c,d only three are known then using the rule ad = bc, we can find the remaining term va=be vd=be »b=ad € ace ad b Example 7: ‘Are the ratios 20 ml : 30 ml and 401 : 50! in proportion ? Solution: 20 ml : 30 ml = 2:3 And 401: 50/ = 4:5 AS23445 ‘So, 20:30 # 40: 50. ‘Therefore, the ratios 20 ml : 30m! and 40/ : 5O/ are not in proportion.Example 8: Do the ratios 18km to $4m and 10 hours to 108 seconds form a proportion? Solution : We have, 18km = 18000m and 10 hours =10 * 60 x 60 seconds = 36000 seconds Consider, 18km : 54m = 18000 : 54 =1000:3 | ‘Also, 10 hours : 108 seconds =36000 : 108 =1000 : 3 ‘Thus, 18k to 54m and 10 hours to 108 seconds form a proportion Example 9: ‘Arainstorm produced a rainfall of 2 inches per hour How many hours would it take to get rainfall amount to one foot? ‘We know that, 1 foot = 12 inches. [Remember before comparing, units should be same] ‘According to question, ratio of rainfall = ratio of number of hours We know if a,b,¢,d are in proportion then ad = be. Here a= 2inches ,b = 12 inches,c = 1hr and d =? m= Ag Itwould take 6 hours to get rainfall amounting to 1 foot. 1. Check if the following are in proportion or not. (a) 3,5,15,25 (b) 18,24,15,20 {c) 63,105,18,30 (4) 24,96,16,54 2. Which of the following statements are true? (a) 60 caps: 200 caps:: 20 monkeys : 60 monkeys. (b)1.2 litres: 24 litres :: 5 Cups : 100 cups __(€) 88 books: 264 books:: % 450 : € 1350 : people: 200 people :: Sky: 25kg 3. Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion. (a) 25 litre: 1m/ and 40kg: 160 - (b) 0.5m: Sem and 0.06kg: 6g (c) 3kg: 40kg and 11g : 66 ees cae The second, third and fourth terms of a proportion are 5, 90 and 25. Find the first term. Fee ea torent zeta a How many seed packets does she need to have 33 flowers? '@ proportion from the following set of numbers (a) 8,2,1,4 (b) 3,7,42,18 —— _.—_—__——VINITAKY METHOD Consider the following problem sums » Rishi bought one pen for % 25. What is the cost of 4 such pens? ® Raman bought 2 tennis balls for & 100. What would be the cost of one tennis ball? You can easily solve both the problems. Cost of 4 pens = % 25x4= 100. Cost of one tennis ball = % 100+2 = % 50, Itis very easy to find the cost of required number of units if the Also it wasn’t difficult either to find the cost of ‘one unit, given tt Let’s now consider the following situation: If the cost of 4 bags is & 320. Find the cost of 6 such bags. We know, to find the cost of 6 bags we should know the cost of one bag. Hf the cost of 4 bags is given to us, we can easily find the cost of one bag Therefore we will solve the above problem sum in two steps: 1. Calculating the cost of one unit. 2. Finding the cost of the required number of units. This method of calculation is called Unitary method. Cost of one unit is known to you, he cost of more number of units Thus the above problem will be solved in the following manner Cost of 4 bags = % 320 Cost of lbag =%320+4=%80 Cost of 6 bags = 80 x 6 = % 480 The cost of 6 bags is & 480. Er nal ab bs in 8 litres of diesel. How much distance will it cover in 3 litres of diesel? Solution: In B litres of diesel, distance travelled by truck= 400 km {In 1 litre of diesel, distance travelled by truck = (400 + 8) = 50 km In 3 litres, distance travelled by truck = 3 x SO km = 150 km. ‘Thus, the truck can travel 150 km in 3 litres of diesel. & Less diesel, less distance= Example 11: If cost of a dozen pencils is & 36, what will be the cost of pencils per score? solution = ‘We know that 1 dozen = 12 and 1 score = 20 Cost of 12 pencils = %36 Cost of one pencil = % 36+ 12=%3 Cost of a score pencils or 20 pencils = 720x3= %60 ‘Thus, the cost of a score pencils is % 60. Example 12: ‘Atrain runs 180 km in ad hours (a) How much time will it take to cover 60 km with the same speed? {b) Find the distance covered by it in 24 hours with the same speed. solution: * {a) We know 1} hours = 3 hours =3% 60= 90 mins Time taken to cover 180km = 90 min = 021 Time taken to cover Lkm 78072 min. Time taken to cover 60km = 3x 60 = 30 min ‘Thus, the train can cover 60km in 30 minutes “(022 hours =3 hours = 5 «60 = 150 mins Distance covered in 90 mins = 180k in 1 min = 180 + 90km = 2km in 150 mins = 150x 2 =300km distance covered is 300km. type 270 pages a day, How many pages can 36 boys type ina. day? typed ina day by 15 boys = 270 | typed in a day by 1 boy = 270+ 15= 18 Number of pages typed in a day by 36 boys = 18 x 36= 648 “Number of pages typed by 36 boys in a day 's 648,—my CT 1. f 19 workers dig 190 holes in an hour, how many holes could thirty workers dig in an hour? 2. Tomake 5 apple pies, Anu requires 3kg of apples. How many kilograms of apples are needed to make 15 pies? 3. Find the cost of 50 litres vegetable oil f the cost of 20 litres is % 2040. 4, Acartravels 90km in 3 hours. (a}Find the distance travelled by car in 5 hours. (b) How much time will the car take to travel a distance of 540km? 5. If six story books weight 66g, what would 170 story books weigh? 6. _Tomake 15 cakes we need 120g of butter. How many cakes can be made from 48¢ of butter? 7. Ima bakery, 1200g of flour is needed to make 30 biscuits. How much flour is needed to make {a) 20 biscuits? (b) 80 biscuits? 8. Cost of 3 dozens soaps is % 900. How many soaps can be purchased for % 1250? Also, find the cost of 12 dozens of soaps. 9. The cost of 15 stamps is € 11.25 (a) Find the cost of 36 stamps. (b) Find the number of stamps that can be bought for & 60.75. 10. The annual income of Abhijit is & 2,76,000. {a) Find his income in 15 months. (b) in how many years will he earn & 8,28,000? 1. Two quantities of the same type can be compared by two ways: comparison by difference and comparison by division. 2. The comparison by division is commonly termed as ratio. 3. _ Inratio a : b, ais known as antecedent and the term b is known as consequent. 4. Equivalent ratios can be obtained by multiplying or dividing the numerator and denominator by ‘the same number. 5. __Iftwo ratios are equal, we say that they are in proportion and use the symbol ‘:’ or ‘=’ to equate the two ratios. 6. If a:b=¢:d then, ad = be where a and d are called extremes and b and c are called means. 7. Unitary method is a method involving two steps: (i) Finding value of one unit. (i) Finding value of the required number of units. {>id x32 = 25,60, 12 and 25 are calles * fi = (g)12 is middle and 25 extreme term t 12 extreme term (c)means (0) 25 is middle and (iy check which of the following are in proportion (ay2,5.45,120 (8) 34, 99, 51,153 (12.14.47 {0) 9,18,23,46 {ui The ratio of one month to one year iS 1:12 (ey iza (dt () The ratio 12: 1315 not equivalent to wy24i26 (8) 6065 (c)108:117 (0) 84:93 {vy Abox contains ‘40 mangoes and 8 were found to be rotten. ‘the fresh mangoes |S waa (isa = (15 Which of the following Is true? tay12 18+ 15: 20 (g) 35: 72= 49:78 (cja2: 54=18:30 (0) 12:10 = 18:15 wi) tf two — third of the audience were adults in a cultural show in which 360 people were what is the total number of children present? (a) 144 (8) 216 (c) 120 (0) 240 (vil) The sum of the angles of a triangle Is 180°. The angles are in the ratio measure of largest angle of the triangle? (ase (8) 60° (c) 90° (0) 120° (x) fa, b, dare in proportion, then (Ajab=cd (B)ac=bd (C)ad=be (0) None of these {x) The simplest form of a ratio 175: 245 ts (2535 (8)35:49—(C)5:7 (0) 10:14 2 Yo, ladaapande non-flowering plants in a park is 3 : 5. If there are 33 flowering : Fr erence in the park? ; Ine rere eS If there are 121 frocks and skirts in the store, . z 3 aes cas et en es will she take to spend & 45000? shaved toancoray® 1402 . How many kilograms of wheat could she have bought if ¢ en 125km in hours. ‘much Pe Re itevenens tv cones 7Skem with the same spaggt BY. aeeeien covered in 4 hours at the same speed. ‘amongst A,B and C in the ratio 3:5:7 WU“ “64 (D) 12:365 The ratio of the rotten mangoes to (D) 5:2 1; 2: 3. What is the