Scribd Logo
Upload

Welcome to Scribd!

  • Mathematics GR 12

    Uploaded by

    reacharunk
    3 views1 page
    This document discusses calculating the gradient of a curve at a point. The gradient is defined as the slope of the tangent line to the curve at that point. It is calculated by taking the limit as h approaches 0 of the difference quotient (f(a+h)-f(a))/h, where a is the x-coordinate of the point and h is the distance to another nearby point Q along the x-axis. As the distance h between the points gets smaller, the secant line joining them approaches the tangent line at the point P.

    Original Description:

    oiuoiuouo

    Original Title

    228403049-Mathematics-Gr-12(223)

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document
    This document discusses calculating the gradient of a curve at a point. The gradient is defined as the slope of the tangent line to the curve at that point. It is calculated by taking the limit as h approaches 0 of the difference quotient (f(a+h)-f(a))/h, where a is the x-coordinate of the point and h is the distance to another nearby point Q along the x-axis. As the distance h between the points gets smaller, the secant line joining them approaches the tangent line at the point P.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    3 views1 page

    Mathematics GR 12

    Uploaded by

    reacharunk
    This document discusses calculating the gradient of a curve at a point. The gradient is defined as the slope of the tangent line to the curve at that point. It is calculated by taking the limit as h approaches 0 of the difference quotient (f(a+h)-f(a))/h, where a is the x-coordinate of the point and h is the distance to another nearby point Q along the x-axis. As the distance h between the points gets smaller, the secant line joining them approaches the tangent line at the point P.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    of 1

    y

    secant
    f (a + h)

    f (a)

    P
    f (x)

    a+h

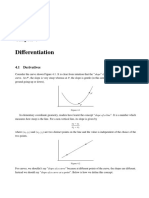
    If we let the x-coordinate of P be a, then the y-coordinate is f (a). Similarly, if the


    x-coordinate of Q is (a + h), then the y-coordinate is f (a + h).
    We can now calculate the average gradient as:
    yQ yP
    f (a + h) f (a)
    =
    xQ xP
    (a + h) a
    f (a + h) f (a)
    =
    h
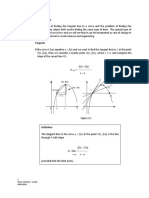
    Gradient at a point
    Imagine that Q moves along the curve, getting closer and closer to P . The secant
    line approaches the tangent line as its limiting position. This means that the average
    gradient of the secant approaches the gradient of the tangent to the curve at P .
    tangent
    y
    secant
    Q
    P

    We see that as point Q approaches point P , h gets closer to 0. If point Q lies on


    point P , then h = 0 and the formula for average gradient is undefined. We use our
    knowledge of limits to let h tend towards 0 to determine the gradient of the tangent to
    the curve at point P :
    Gradient at point P = lim

    h0

    212

    6.1. Limits

    f (a + h) f (a)
    h

    You might also like