c 7.2.

CALCULUS OFVARIATIONS 2006Gilbert Strang

7.2 Calculus of Variations
One theme of this book is the relation of equations to minimum principles. To
minimize P is to solve P

= 0. There may be more to it, but that is the main

1
point. For a quadratic P(u) =
2
u
T
Ku u
T
f, there is no diculty in reaching
P

=Kuf =0. The matrix K is symmetric positive denite ataminimum.

Inacontinuousproblem,thederivativeofP isnotsoeasytond. Theunknown
u(x)is afunction, andP(u)is usually an integral. Its derivative P/uis called the
rst variation. The Euler-LagrangeequationP/u=0hasaweak form
and a strong form. Foran elastic bar,P is the integral of
1
c(u

(x))
2
f(x)u(x).
2
The equation P/u=0 is linear andthe problem will have boundary conditions:

cu

dx=

v (cu

=f(x). Weak form fvdxforevery Strong form

Our goalin this section is to getbeyond this rst example ofP/u.
The basic idea should be simple and it is: Perturb u(x) by a test function
v(x). ComparingP(u)withP(u+v),thelinearterminthedierenceyieldsP/u.
This linear term must be zero for every admissible v (weak form). This program
carries ordinary calculus into the calculus ofvariations. We doit in several steps:
1. One-dimensional problems P(u)= F(u,u

)dx,not necessarily quadratic

2. Constraints, notnecessarily linear, with their Lagrangemultipliers
3. Two-dimensional problems P(u)= F(u,u
x
,u
y
)dxdy
4. Time-dependent equations in which u

=du/dt.
At each step the examples will be as familiar (and famous) as possible. In two
dimensions that means Laplaces equation, and minimal surfaces in the nonlinear
case. In time-dependent problems it means Newtons Laws, and relativity in the
nonlinear case. Inone dimension we rediscover the straight line and the circle.
This section is also the opening to control theorythe modern form of the
calculus of variations. Its constraints are dierential equations, and Pontryagins
maximum principle yields solutions. That is awhole world ofgoodmathematics.
Remark Togofromthestrongformtotheweakform,multiply by v and integrate.
For matrices the strong form is A
T
CAu = f. The weak form is v
T
A
T
CAu = v
T
f for
allv.
For functions with Au=u

, this exactlymatches cu

dx= fvdx above.

c 2006Gilbert Strang
One-dimensional Problems
The basic problem is to minimize P(u)with a boundary condition ateach end:

1
P(u)= F(u,u

)dx with u(0)=a and u(1)=b.

0
Thebestudefeatseveryothercandidateu+vthatsatisestheseboundaryconditions.
Then (u+v)(0)= a and (u+v)(1) =b require that v(0)= v(1)= 0. When v and
v

aresmallthecorrectiontermscomefromF/uandF/u

. Theydontinvolve
v
2
:
F F
Inside the integral F(u+v,u

+v

)=F(u,u

)+v +v

+
u u

1
F F
After integrating P(u+v)=P(u)+ v +v

dx+
u u

0
That integrated term is the rst variation. We have already reached P/u:
P

1
F F
Weak form = v +v

dx=0 forevery v. (1)

u
0
u u

This is the equation for u. The derivative of P in each direction v must be zero.
Otherwise we can make P/unegative, which would mean P(u+v)<P(u): bad.
Thestrongformlooksforasinglederivative whichifitiszeromakes allthese
directional derivatives zero. Itcomes from integratingP/uby parts:

1

1
F d F F
Weak form / by parts v
u
v
dx u

dx+ v =0.
u

0
0
The boundary term vanishes because v(0) = v(1) = 0. To guarantee zero for every
v(x) inthe integral, the function multiplying v must be zero(strong form):
u
d
dx

. (2) Euler-Lagrange equation for

F
u
F
u
=0
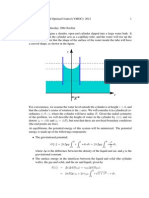
Example Find the shortest path u(x)between two points (0,a)and(1,b).
ByPythagoras, (dx)
2
+(du)
2
isashortsteponthepath. SoP(u

)= 1+(u

)
2
dx
isthelengthofthepathbetweenthepoints. ThissquarerootF(u

)dependsonlyonu

andF/u=0. The derivativeF/u

brings the square rootintothe denominator:

F

1
u

Weak form = v

dx=0 forevery v with v(0)=v(1)=0. (3)

u
0 1+(u

)
2
If the quantity multiplying v

is a constant, then (3) is satised. The integral is

certain to be zero because v(0) = v(1) = 0. The strong form forces F/u

to be
PSfrag replacements

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang
constant: the Euler-Lagrange equation (2)is
d F d u

= =c. (4)
dx u

dx
1+(u

)
2
=0 or
1+(u

)
2
That integration is always possible when F depends only on u

(F/u=
0). It leaves the equation F/u

=c. Squaring bothsides, uis seen to belinear:

c
2
(u

)
2
=c (1+(u

)2) and u

=
1
c
c
and u=
1c
x+d. (5)
2 2
Theconstantscanddarechosentomatchu(0)=aandu(1)=b. Theshortestcurve
connectingtwo points is a straight line. Nosurprise! ThelengthP(u)isaminimum,
nota maximum orasaddle point, because the second derivative F

is positive.
u= optimalarc
u+v
perturbed
b b
a a
x
0 1 0 1
typical perturbationv(x)
area below arc is A
Figure7.5: Shortest paths froma tob: straight line and circular arc (constrained).
v
u=

1
m

1
m
optimalline
Constrained Problems
Supposewecannotgoinastraightlinebecauseofaconstraint. Whentheconstraint
is u(x)dx=A, we look forthe shortest curve that has area A below it:

1
Minimize P(u)= 1+(u

)
2
dx with u(0)=a, u(1)=b, u(x)dx=A.
0 0
The areaconstraint should bebuilt intoP by aLagrangemultiplierhere called m.
Themultiplierisanumberandnotafunction,becausethereisoneoverallconstraint
rather thana constraint atevery point. The LagrangianLbuilds in udx=A:
Lagrangian L( P

(F +mu)dx u,m)= +(multiplier)(constraint)= mA.

The Euler-Lagrangeequation L/u=0is exactly like P/u=0in (2):
(F +mu) d (F +mu) d u

=m
dx

1+(u

)
2
=0. (6)
u

dx u

c 2006Gilbert Strang
Againthis equation is favorable enough to beintegrated:
u

mx =c which gives u

=
mxc
.
1+(u

)
2
1(mxc)
2
After one moreintegration we reach the equation ofacircle in the x-uplane:
u(x)=
1
1(mxc)
2
+d and (mxc)
2
+(mud)
2
=1. (7)
m
The shortest path is a circular arc! It goes high enough to enclose area A.
The three numbers m,c,d are determined by the conditions u(0)=a,u(1)=b, and
udx=A. The arcis drawn inFigure 7.5(and m is negative).
We now summarize the one-dimensional case, allowing F to depend also on u

.
Thatintroduces v

intothe weak formandneeds two integrations by partstoreach

the Euler-Lagrange equation. When F involves a varying coecient c(x), the form
ofthe equation does not change, because it is uand notx thatis perturbed.
Therst variationofP(u)=

1
0
F(u, u

, u

, x)dxis zero at aminimum:

Weak
form
P
u
=

1
0

v
F
u
+v

F
u

+v

F
u

dx=0 forallv.
TheEuler-Lagrangeequation fromintegration byparts determines u(x):
Strong
form
F
u

d
dx

F
u

+
d
2
dx
2

F
u

=0.
Constraints onubring Lagrangemultipliers andsaddle points ofL.
Applications are everywhere, and we mention one (of many) in sports. What
angle is optimal in shooting a basketball? The force of the shot depends on the
launch angleline drives or sky hooks need the most push. The force is minimized
at 45

if the ball leaves your hand ten feet up; for shorter people the angle is about
50

. Whatisinterestingisthatthesameanglesolvesasecondoptimizationproblem:
tohave the largest margin oferrorand still gothrough the hoop.
The condition is P

=0 in basketball (one shot) and P/u=0in trackwhere

the strategy tominimize the time P(u)has been analyzed forevery distance.
Two-dimensional Problems
In two dimensions the principle is the same. The starting point is aquadratic P(u),
without constraints, representing the potential energy over aplane region S:

2

2

c u c u
Minimize P(u)=
2 x
+
2 y
f(x,y)u(x,y) dxdy.
S

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang
If this energy has its minimum at u(x,y), then P(u+v) P(u) for every v(x,y).
We mentally substitute u+v in place ofu,and look forthe term that is linear in v.
That term is the rst variationP/u,which must be zero forevery v(x,y):
=

S

c +c

. (8) Weak form

P
u
u
x
v
x
u
y
v
y
fv dxdy=0
This is the equation of virtual work. It holds for all admissible functions v(x,y),
and it is the weak form of Euler-Lagrange. The strong form requires as always an
integrationbyparts(Greensformula),inwhichtheboundaryconditionstakecareof
the boundary terms. Inside S, thatintegration moves derivatives away fromv(x,y):

u u
Integrate by parts
x
c
x

y
c
y
f vdxdy=0. (9)
S
Now the strong form appears. This integral is zero forevery v(x,y). By the funda-
mentallemmaofthecalculusofvariations,theterminbrackets isforcedtobezero
everywhere:
u u
Strong form
x
c
x

y
c
y
=f(x,y) throughoutS. (10)
This is the Euler-Lagrangeequation A
T
CA=f,orcu=f. Forconstant cit
is Poisson. If the y variable is removed, we are back to aone-dimensional rod.
With no extra eortwe can gobackwards to P(u)fromany linear equation:

2
u
2
u
2
u
Second-order equation a +2b +c =0. (11)
x
2
xy y
2
When a,b, and c areconstant, the corresponding quadratic energy is

2

2
1 u u u u
P(u)= a +2b +c dxdy.
2 x x y y
If we minimize P we expect to reach (11) as its Euler equation. But there is more
to it than that. To minimize P it should be positive denite. Inside the integral is
an ordinary 2 by 2 quadratic au
2
x
+2bu
x
u
y
+cu
2
y
. The test for positive-deniteness
is still ac>b
2
, as it was in Chapter 1. (We can make a>0 in advance.) That test
decides whether or not equation (11) can be solved with arbitrary boundary values
onu(x,y).
In this positive denite case the equation is called elliptic and minimization is
justied. There arethree fundamental classes ofpartialdierential equations:

c 2006Gilbert Strang
au
xx
bu
xy
+cu is elliptic

a b
b c

:
E
P
H
2
ac=b
2
2
( )
( )
( )
The partial dierential equation +2
yy
=0 or parabolic or
hyperbolic, according tothe matrix
ac>b elliptic boundary-valueproblems
parabolicinitial-valueproblems
ac<b hyperbolicinitial-valueproblems
steady state equations
heat/diusion equations
wave/convection equations
Laplaces equation u
xx
+u
yy
= 0 is elliptic, with a = c = 1 producing the identity
matrix. The heat equation u
xx
u
t
= 0 is parabolic, with b = c = 0; the matrix is
singular and its determinant is zero. That parabolic borderline between elliptic and
hyperbolic needs help from lower-order terms. The wave equation u
xx
u
tt
=0 has
a=1andc=1. Itasks forinitialvaluestwo conditions onpartofthe boundary
and noconditions onanother part,instead ofone condition everywhere.
Here we stay with elliptic equations and minima of P(u). The boundary con-
ditions can specify u, or they can specify the normal component w n.
Comparing (8) with (9), the boundary term comes from Greens formula in Sec-
tion :
u vdxdy= u))vdxdy+ (cu n)vds. (12) c ( (c
S S C
Both sides equal fvdxdy; that is the weak form. The rst term on the right
yields thestrongformdiv(cgradu)=f(x,y). Azerointegralover the boundaryc
in(12)willbeachievedbytheboundaryconditions. Strictlyspeaking,theboundary
conditions onu(x,y)are partofthe strong form.
There are two ways to make this boundary integral of (cu n)v safely zero. If
boundary values u=u
0
are given, and u+v shares those values, then v =0 on the
boundary. Thatkillstheintegral. Whenuisnotgivenandv isfree,wemustimpose
the naturalboundary condition cu n=w n=0.
A natural condition on w goes with A
T
. The essential condition u = u
0
goes
with A.
The Minimal Surface Problem
Now we are ready for nonlinear partial dierential equations. The corresponding
energy will not be a quadratic P(u). It will be the exact energy E(u), from which
P originallycame asanapproximation. Ifthere isathinmembrane covering theset
Slike a soap bubblethen stretching this membrane requires energy. The energy
is proportional to the surface area of the soap bubble. In the right units the
material constant will be c = 1, and the problem is to minimize the surface

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang

area E(u):

2

2

1/2
u u
Choose u(x,y) to minimize E(u)= 1+ + dxdy. (13)
x y
S
When u = 0, the bubble is at. The expression in brackets reduces to 1. That is
the minimum ifu=0 is admissible. But suppose the bubble is created on apiece of
wire thatgoes around S at avarying height u
0
(x,y). The bubble has to stick to the
wire, sothe trivial solution u=0is not allowed. The bent wire imposes a boundary
condition u = u
0
(x,y) at the edge of S, and the minimal surface problem is to
nd the smallest areaE(u). Physically, surface tension makes the areaaminimum.
The test for a minimum is still E(u) E(u+v). To compute the term E/u
thatislinearinv,lookatthepartAfromualone,andthecorrectionB involvingv:

2

2
u u u v u v
A=1+ + and B =2 +2 +O(v
2
).
x y x x y y
Forsmallv,thesquarerootis

A+B =

A+B/2

A+ . Integratebothsides:
1 u v u v
E(u+v)=E(u)+ + dxdy+ . (14)
A
x x y y

S
NowE/uisexposed. Itistheintegralin(14)anditiszero. Thatistheweakform
of the minimal surface equation. Because of the square root of A, it is not linear in
u. (Itisalways linearinv;thatisthewholepointoftherstvariation!) Integrating
by parts to remove the derivatives from v produces the Euler equation in its strong
form:

Minimal surface
equation

x
1

A
u
x

y
1

A
u
y
=0. (15)
Thisisnoteasytosolve,becauseofthesquarerootinthedenominator. Fornearly
at bubbles, linearization approximates

A by 1. The result is Laplaces equation.

Perhaps it is only natural that the most important nonlinear equation in geometry
should reduce to the most importantlinear equation, butstill itis beautiful.
Nonlinear Equations
The shortest distance and minimal surface problems are typical of the general case.
ThevariationalproblemstartswithanintegralE = Fdxdy. ThenF dependson
x and y and uand derivatives like u/x:
F =F(x,y,u,D
1
u,D
2
u,...).
For an elastic bar there was only D
1
u = u/x. For a soap bubble there is also
D
2
u=u/y. Higher derivatives are allowed, and we can think ofuitself as D
0
u.

c 2006Gilbert Strang
ThecomparisonofE(u)withthenearbyE(u+v)startsfromanordinaryexpan-
sionlike F(u+v)=F(u)+F

(u)v+O(v
2
). WhenF dependsonseveral derivatives
ofu,this expansion hasmore terms fromF(x,y,D
0
u+D
0
v,D
1
u+D
1
v,...):

F
Inside the integral F(u+v)=F(u)+ D
i
v+ . (16)
D
i
u

We take the derivatives of F with respect to u and u
x
and any other D
i
u.
The weak form involving v deals with those linear terms: (integral=0 for all v).
The strong form lifts each derivative D
i
from v and puts it (as D
i
T
) onto the part
involving u:

F F
Weak to Strong (D
i
v)dxdy D
T
vdxdy
D
i
u
i
D
i
u
The transpose is D
T
= D
i
for derivatives of odd order (with an odd number of
i
integrations by parts andminus signs). Foreven derivatives D
T
=+D
i
.
i
BuriedinsidethecalculusofvariationsistherealsourceofA
T
CA! Thederivatives
D
i
u give Au. Their transposes D
T
give A
T
. In between, C is normally nonlinear.
i
ButwhenF isapurequadratic
1
c(Du)
2
,thenD
T
F/DubecomesD
T
(cDu)which
2
is exactly the linear A
T
CAuthe we know so well.
7G Eachproblem inthe calculus of variationscanbe stated inthree forms:
Variational form MinimizeE(u)= F(x,y,u,D
1
u,D
2
u,...)dxdy

S
E

F
Weak form = (D
i
v)dxdy=0 forallv
u D
i
u
S

F
Euler-Lagrange strong form D
T
=0.
i
D
i
u
2 2 2
Example 1 F =u
2
+u +u
2
+u +u
2
+u
yy
=(D
0
u)
2
+
x y xx xy
+(D
5
u)
2
The derivatives of F (a pure quadratic) are 2u,2u
x
,2u
y
,...,2u
yy
. They are derivatives
with respect to uandu
x
andthe other D
i
u,not with respect tox!
Weak form 2 [uv+u
x
v
x
+u
y
v
y
+u
xx
v
xx
+u
xy
v
xy
+u
yy
v
yy
]dxdy=0.
We integrate every term byparts togive the strong form(times v):
Strong form 2 [uu
xx
u
yy
+u
xxxx
+u
xyxy
+u
yyyy
] =0.
Thisis linear because F is quadratic; the minus signs come with oddderivatives in F.

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang

2 2
Example 2 F =(1+u
x
)
1/2
or F =(1+u
2
+u
y
)
1/2
x
The derivatives with respect to u
x
and u
y
bring the square root into the denominator.
Theshortest pathequation andthe minimal surface equation are
d u
x
u
x
u
y
=0.
2

dx(1+u
x
)
1/2
=0 and
x F

y F
Everyterm ts into the pattern ofA
T
CA, andthe framework becomes nonlinear:
F
e=Au w=C(e)= leads to A
T
w=A
T
C(Au)=f.
nonlinear e
Nonlinear C(Au) from Nonquadratic Energies
That last line was worth a chapter of words. It is the shortest path to nonlinear
equilibrium equations. In a linear spring, w = ce is proportional to e. The internal
2
strain energy is F = cede =
1
ce . In a nonlinear spring the constitutive
2
law is w = C(e). The relation of force to stretching, or current to voltage, or ow
topressure, is nolonger astraight line Ce. We need parentheses in C(e)!
The energy density is still F = C(e)de = force times movement. Minimizing
the totalenergy (integrate F tond E) still gives the equilibrium equation:
The energy P(u)= [F(Au)fu]dx is minimized when A
T
C(Au)=f.
The rst variationofE leads to [C(Au)(Av)fv]dx=0forevery v (weak form).
Then A
T
C(Au)=f is the Euler equation (strongform).
For the nonlinear equivalent of positive deniteness, the function C(e) should be
increasing. The linew=cehadaconstant slopec>0. NowthatslopeC

=dC/de
is changingbut it is still positive. That makes the energy E(u) a convex function.
The Euler equation is ellipticwe have aminimum.
An example is the power law w=C(e)=e
p1
with p>1. The energy density is
itsintegralF =e
p
/p. Thestretchingise=Au=du/dx. Theequilibriumequationis
A
T
C(Au)=( d/dx)(du/dx)
p1
=f. This is linear forp=2. Otherwise nonlinear.
Complementary Energy
The complementary energy is afunction ofw instead ofe. Itstarts with the inverse
constitutive law e=C
1
(w)in our example e=w
1/(p1)
. The strain e comes from
the stress w; the arrow in our framework is reversed. Graphically, we are looking at
Figure 7.6a from the side. The area under that curve is the complementary
energy density F

(w)= C
1
(w)dw. The twin equations come fromF andF

:
F F

Constitutive Laws w=C(e)= and e=C

1
(w)= . (17)
e w
PSfrag replacements
PSfrag replacements

c 2006Gilbert Strang
ThesymmetryisperfectandthedualminimumprincipleappliestoQ(w)= F

(w)dx:
The complementary energy Q(w) is a minimum subject to A
T
w=f(x).
ALagrangemultiplieru(x)takesQtoL(w,u)= [F

(w)uA
T
w+uf]dx,withthe
constraintA
T
w=f builtin. Itsderivativesrecoverthetwoequationsofequilibrium,
now nonlinear:
L/w=0 is C
1
(w)Au=0
L/u=0 is A
T
w =f.
The rst equation gives w=C(Au)andthen the second is A
T
C(Au)=f.
w w
F(w)
e
area F +F

ew
F

(e)
e=C
1
(w)
w=C(e)
e
areaF +F

so w=C(e)
e
w
ofrectangle is >ew
Figure 7.6: The graphs ofw=C(e)and e=C
1
(w),andtheir areas F

and F.
Since these nonlinear things are in front of us, why not take the last step? It is
never seen in advanced calculus, but there is nothing so incredibly dicult. Itis the
direct link between F andF

, known asthe Legendre-Fenchel transform:

F

(w)=max [ewF(e)] and F(e)=max [ewF

(w)]. (18)
e w
Fortherstmaximum,dierentiatewithrespecttoe. Thatbringsbackw=F/e,
which is the correct C(e). The maximum itself is F

= eF/eF. The gures

show graphicallythattheareassatisfy F

=ewF onthecurve andewF <F

othe curve. So the maximum ofewF is F

as desired.
Similarly, the second maximum in (18) leads to e = F

/w. That is the con-

stitutive law in the other direction, e = C
1
(w). The whole nonlinear theory is
there, provided the material laws are conservativethe energy in the system should
be constant. This conservation law seems to be destroyed by dissipation, or more
spectacularly by ssion, but in some ultimate picture ofthe universe itmust remain
true.
mu
F will be the Lagrangian and F

is the Hamiltonian. The equations

tt
+cu
t
+ku = 0 and u
xx
= u
t
include friction and damping and diusion, but
we hesitate to stretch our framework that far. Feynmans wonderful lectures made
least actionthe starting point forphysics, and the next paragraphs.
c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang
The Legendre transform reappears at full strength in constrained optimization.
ThereF andF

aremoregeneralconvexfunctions(withnonnegativesecondderiva-
tives)andwe recognize that F

is F. HerewecomputeF

(w)forthepowerlaw
and verify thatit agrees with the integral ofC
1
(w).
Example Find F

(w)for the power law F(e)=e

p
/p(e>0andw>0andp>1)
Dierentiating ewF(e) gives we
p1
= 0. Then the conjugate F

(w) in (18) is
w
q
/q:
1 1 1
p/(p1) p/(p1)
e
p
F

=ew =w
1/(p1)
w w =
p1
w = w
q
.
p p p q
F

(w) = w
q
/q is also a power law, with dual exponent q = p/(p1). This matches
the area under C
1
(w) = w
1/(p1)
, because integration will increase that exponent to
1+1/(p1)=q. The symmetric relationbetween the powers is p
1
+q
1
=1.
Dynamics and Least Action
Fortunately or unfortunately, the world is not in equilibrium. The energy stored in
springsandbeamsandnucleiandpeopleiswaitingtobereleased. Whentheexternal
forces change, the equilibrium is destroyed. Potential energy is converted to kinetic
energy,thesystembecomesdynamic,anditmayormaynotndanewsteadystate.
When the system is conservative, the transients will not grow or decay. The
energy changes frompotentialtokinetic topotentialtokinetic, but thetotalenergy
K+P remainsconstant. Itisliketheeartharoundthesunorachildonafrictionless
swing. The force dP/du is no longer zero, and the system oscillates. The problems
are dynamic instead ofstatic.
Todescribethemotionweneedanequationoravariationalprinciple. Numerically
we mostly work with equations (Newtons laws and conservation laws). This section
derives those laws fromthe principle of least action:
The actualpathu(t)minimizes theactionintegral A(u)between theinitial state
u(t
0
) andthe nal state u(t
1
):

t
1
A(u)= (kinetic energypotential energy)dt.
t
0
It is better toclaim only that A/u=0the pathis always astationary point but
notineverycircumstance aminimum. Wehaveadierence ofenergies, andpositive
deniteness canbelost(asaddlepoint). Laplacesequationwillbeovertaken bythe
waveequation. Firstcomethreeexamplestoshowhowtheglobal law ofleastaction
(the variationalprinciple ofleast action) produces Newtons local law F =ma.
Example 3 A ballofmass m is attracted by the Earths gravity

c 2006Gilbert Strang
Theonlydegree offreedom is the balls height u(t). Theenergies are K andP:

2
1 du
K =kinetic energy= m and P =potential energy=mgu.
2 dt
The action is A = (
1
m(u

)
2
mgu)dt. Then A/u follows from the rules of this
2
sectionwith the time variable t replacing the space variable x. The true path u is
compared to its neighbors u+v. The linear part of A(u+v)A(u) gives the rst
variationA/u=0:
A
t
1
= (mu

mgv)dt=0 forevery v.
u
t
0
That is the weak form of Newtons law. You recognize the momentum mu

as the
1
m(u

)
2
derivative of with respect to the velocity u

. The strong form is the Euler

2
equation:
d du
Newtons law m mg=0 which is ma=F. (19)
dt dt
The action integral is minimized by the path that follows Newtons law.
The 3-step framework of applied mathematics is not changed. The place of A is
taken by d/dt and A
T
is d/dt. The material constant is m and the external force is
f = mg. The balance between A
T
CAu and f is Newtons lawa balance of inertial
forcesinsteadofmechanicalforces. Figure7.7identiesthevariablesasthevelocityand
momentum.
position u
velocity v momentum p
force f

. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . . . . . . . . . .
. . . . . . . . . .
. . . . . . .
. .. . .. . .. .
..................................................................................... ............... .... .

l
llcos

du dp
. . . . . .
v= f =
....
. . . . . . . . . .
. . . . . . . . .
dt dt
. . . . . . . . . . .
. . . . . ... . .
. . . . . . . . . .
. . ... . ... .
. . . . . . . . . .
. . .. . . ... . . . . . . . . . . . .
. ..
p=mv
Figure 7.7: Newtons law foraball. A pendulum alsots the framework.
Example 4 A simple pendulum with mass m andlength l
Thestatevariableuistheangle fromthevertical. Theheightllcosstillentersthe
potentialenergy and the velocityis v=ld/dt:

2
1 d
K =kinetic energy= ml
2
and P =potential energy=mg(llcos)
2 dt

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang

Inthisproblemtheequationwillnolongerbelinear. K isquadraticbutP involvescos.
TheEuler equationfollows the rule for anintegral F(,

)dt,with F =KP:
Euler F d F d d
equation

dt

=0 or mglsin ml
2
=0.
dt dt
Thisis the equation ofasimple pendulum. Themass cancels out;clocks keep time!
d
2
g
Pendulum equation + sin=0. (20)
dt
2
l
Whentheangleissmallandsinisapproximatedby,theequationbecomeslinear. The
periodchanges a little. A linear clock keeps time, but not the righttime.
Example 5 A verticalline ofsprings andmasses has Mu

+Ku=0
1
ThepotentialenergyinthespringsisP =
2
u
T
A
T
CAu. Thekineticenergyhas
1
m
i
(du
i
/dt)
2
2
from each mass. Then KP goes into the action integral, and there is an Euler equa-
tion A/u
i
=0 for each mass. In matrix form this is the basic equation of mechanical
engineering:
Undamped oscillation Mu

+A
T
CAu=0.
M is the diagonal mass matrix and A
T
CA is the positive denite stiness matrix. The
system oscillates around equilibrium andthe totalenergy K+P is constant.
Example 6 Wavesinan elastic baracontinuum ofmasses and springs.
Theaction integral inthis continuous case hasan integralinstead ofasum:

t
1

1

2

2
1 du 1 du
Action A(u)=
2
m
dt

2
c
dx
dxdt.
t
0
x=0
TheEuler-Lagrangerules forA/u=0cover this case ofa doubleintegral:
A u u
Wave equation
u
=
t
m
t

x x
=0. c
Thatis the wave equation mu
tt
=cu
xx
. Withconstant density m andelastic constant
c, the wave speed is c/mfasterwhen the baris stier andlighter.
Staying with the calculus ofvariations, there are two importantcomments:
1. When u is independent of time (no motion), the kinetic energy is K = 0 and
the least action principle reduces to P/u = 0. The dynamic problem goes
back to the static problem ofA
T
CAu=f, without atime derivative.
c 2006Gilbert Strang
2. The dual variable w, from all the evidence, should be found in its usual place
in Figure7.7. It is the momentum p=mv=mdu/dt. We can rewrite K:
1
2
1
2
The kinetic energy K = mv becomes p .
2 2m
That is the complementary kinetic energy, expressed in terms of p instead of v.
Note that m moves to the denominator, just as c did in the elastic energy w
2
/2c.
Hamilton found the right totalenergy, using the momentum p and the displacement
u. Those variables (not the velocity!) are at the primal and dual corners of our
framework:
1
Hamiltonian H =K+P = p
2
+mgu. (21)
2m
The HamiltonianH(p,u)takes us directly to the equations ofmotion:
=
du
dt
and =
dp
dt
. (22)
:
dH
dt
=
dp
dt
+
dH
du
du
dt
=u

. (23)
Hamiltons equations
H
p
H
u
The derivative dH/dtis zero sothe total energy is constant
Chain rule
H
p
=0
This is the essence ofclassical mechanics. It is tied toHamilton andnot toNewton.
For that reason it survived the revolution brought by Einstein. We will see that H
has a relativistic form and even a quantum mechanical form. Comparing a falling
ball with anoscillating spring, the key dierence in H is between uand u
2
:
1 1
(ball) H = p
2
+mgu (spring) H = p
2
+
1
2
cu
2m 2m 2
Hamiltons equations H/p=u

and H/u=p

yield Newtons Laws:

p
(ball) =u

and mg=p

, or mu

=mg
m
p
(spring) =u

and cu=p

, or mu

+cu=0.
m
The mass passes through equilibrium at top speed (all energy in K). The force
reverses to slow it down and stop it (all energy in P). In the up plane (the phase
plane) the motion stays on the energy surface H = constant, which is the ellipse in
Fig.7.8. Each oscillation ofthe spring is a triparound the ellipse.
Withmorespringsthereare2naxesu
1
,...,u
n
,p
1
,...,p
n
andtheellipsebecomes
an ellipsoid. Hamiltons equations are H/p
i
= du
i
/dt and H/u
i
= dp
i
/dt.
TheyleadagaintoMu

+Ku=0,andtothewaveequationinthecontinuouscase.
7.2. CALCULUS OF VARIATIONS

c 2006Gilbert Strang
1 2 3 4
1
2
3
4
momentum p(t)
height
u(t)
Phase plane
............................................................... . .. . .. . . . . . . . . . . . . . . . . . .
.. .. .. .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. .. .. .. .................................
............................................................... . .. . .. . . . . . . . . . . . . . . . . . .
.. .. .. .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . .. . . . . . . . . . . . .
............................................................... . .. . ..
.. .. .. .. .
. . . . . . . . . . . . . . .
................................
............................................................... . .. . .. . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . .
................................................................ . .. . .. . . . . . . . . . . . . . . . . .
.. .. .. .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .. .. .. .. .................................
............................................................... . . .. . .. . . . . . . . . . . . . . . . . .
.. .. .. .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
X
..................................... .......................... .. . .. . .. . . . . . . . . . . . . . . . .
. . . . .. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . . . . . . .. .. .. .. ..................................
................................................................ . .. . .. . . . . . . . . . . . . . . . . .
. .. .. .. .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
..................................... .......................... .. . .. . .. . . . . . . . . . . . . . . . .
. . . . .. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . .
................................
................................................................ . .. . .. . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . .
..................................... .......................... .. . .. . .. . . . . . . . . . . . . . . . .
. . . . .. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . .
X
................................
............................................................... .. . .. . .. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .
............................................................... .. . .. . .. . . . . . . . . . . . . . . . .
.. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . . . . . . .. .. .. .. ..................................
............................................................... .. . .. . .. . . . . . . . . . . . . . . . .
.. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . . . . . .
all P
............................................................... .. . .. . .. . . . . . . . . . . . . . . . .
.. .. .. .. ..
. . . . . . . . . . . . . . . . . . . . . . . . . . .
. . .. . . . . . . . . . . . . . . . .. . . . . . . . . . . . .

................................
............................................................... .. . . . . . . . . . . . . . . . .
X
all K
X

all K
Figure7.8: 1tension2motion3compression4motion: ConstantenergyH =K+P.
Relativity and Quantum Mechanics
These fewparagraphsareanattempt,byatotalamateur,tocorrecttheactioninte-
gralbytherulesofrelativity. Feynmanslecturesproposethetermmc
2
1(v/c)
2
intheLagrangianKP. Atv=0weseeEinsteins formulae=mc
2
fortheenergy
in amass mat rest. It becomes partofthe potential energy P.
As the velocity increases from zero there is also a part corresponding to K. For
smallxthesquarerootof1xisapproximately1
1
x,whichlinearizestheproblem
2
1
and brings back Newtons
2
mv
2
just as linearizing the minimal surface equation
brought back Laplace. Relativity mixes together K and P!

1v
2
2
Lagrangian F(v)=mc
2
1(v/c)
2
mc 1 .
2c
2
Now,trustinginduality,welookfortheconjugatefunctionF

intheHamiltonian.
It will be a function of p, not v. The rst step is to nd that momentum p. Before
1
relativity, F was
2
mv
2
and its derivative was p=mv. Always p is F/v:
F mv
Momentum p= = . (24)
v
1(v/c)
2
This becomes innite as v approaches the speed oflight. According to (18), F

is
2
Hamiltonian F

(p)=max [pvF(v)]=mc 1+(p/mc)

2
. (25)
v
Thismaximumoccursat(24)whichwesolvedforvandsubstitutedintopvF(v).
2
The new Hamiltonian F

is again Einsteins energy e=mc when the system is

atrest. As pincreases fromzero, the next contribution is Newtons p
2
/2m:
2
2
p
F

mc 1+
1 p
2
= rest energy + .
2m
2
c
2
2m

c 2006Gilbert Strang
Newton found the low-order term in the energy F

that Einstein computed exactly!

Perhapstheuniverseislikeaminimalsurfaceinspace-time. ToLaplaceandNewton
it looked at(linearized), but toEinstein it became curved.
It is risky to add anything about quantum mechanics, which works with proba-
bilities. It is a mixture of dierential equations (Schr odinger) and matrix equations
(Heisenberg). The event at which A/u = 0 almost always occurs. Feynman gave
eachpossibletrajectoryofthesystemaphasefactore
iA/h
multiplyingitsprobability
amplitude. Thesmallnumberh(Plancksconstant)meansthataslightchangeinthe
actionAcompletely altersthephase. There arestrongcanceling eectsfromnearby
pathsunless the phaseis stationary. InotherwordsA/u=0atthemostprobable
path.
This prediction of stationary phase applies equally to light rays and particles.
Opticsfollowsthesameprinciplesasmechanics,andlighttravelsbythefastestroute:
least action becomes least time. If Plancks constant could go to zero, the
deterministic principles of least action and least time would appear and the path
ofleast action would be not only probable but certain.
Problem Set 7.2
1 Whataretheweak formandthestrongformofthelinearbeamequationthe
Euler equation forP = [
1
fu]dx?
2
c(u

)
2
2 MinimizingP = (u

)
2
dxwithu(0)=aandu(1)=balsoleadstothestraight
line through these points. Write down the weak formand the strongform.
3 Find the Euler equations (strongform) for
u 2
(a) [(u

)
2
+e ]dx (b) uu

dx (c) x (u

)
2
dx
4 If F(u,u

) is independent of x, as in almost all our examples, show from the

EulerequationandthechainrulethatH =u

F/u

F isconstant. Thisis
dual tothe factthat F/u

is constant when F is independent ofu.

5 Ifthe speed is x the travel time ofa lightray is

1
1
T = 1+(u

)
2
dx with u(0)=0 and u(1)=1.
0
x
(a) From equation T/u=0 whatquantity is constant (Snells law)?
(b) Can you integrate once more tond the optimal path u(x)?
6 Withthe constraints u(0)=u(1)=0and udx=A, show thattheminimum
value of P = (u

)
2
dx is 12A
2
. Introduce a multiplier m, solve the Euler
equationforu,andverifythatA=m/24. ThenthederivativedP/dA=24A
equals the multiplier m as the sensitivity theory predicts.

c 7.2. CALCULUS OFVARIATIONS 2006Gilbert Strang
7 For the shortest path constrained by udx = A, what is unusual about the
solution in Fig.7.5as Abecomes large?
8 Suppose the constraint is udx A, with inequality allowed. Why does the
solution remainastraight line asAbecomes small? Where does themultiplier
m remain? This is typical of inequality constraints: either the Euler equation
is satised orthe multiplier is zero.
9 Suppose the constrained problem is reversed, and we maximize the area P =
udxsubjecttoxedlengthI = 1+(u

)
2
dx,withu(0)=aandu(1)=b.
(a) Form the Lagrangianand solve its Euler equation foru.
(b) How is the multiplier M related to min the text?
(c) When dothe constraints eliminate all functions u?
10 Find by calculus the shortest broken-line path between (0,1) and (1,1) that
goes rst to the horizontal axis y = 0 and bounces back. Show that the best
pathtreats this axis like amirror: angleofincidence =angle ofreection.
11 Theprincipleofmaximumentropyselectstheprobabilitydistributionthatmax-
imizes H = ulogudx. Introduce Lagrange multipliers for the constraints
udx = 1 and xudx = 1/a, and nd by dierentiation an equation for u.
ax
Ontheinterval0<x<showthatthemostlikelydistributionisu=ae .
12 If the second moment x
2
udxis also known show that Gauss wins again: the
maximizing u is the exponential of a quadratic. If only udx = 1 is known,
themostlikelydistributionisu=constant. Theleast informationcomeswhen
onlyoneoutcomeispossible,sayu(6)=1,sinceuloguisthenidenticallyzero.
13 A helix climbs aroundacylinder with x=cos,y=sin,z =u():
its length is L= dx
2
+dy
2
+dz
2
= 1+(u

)
2
d.
Show that u

=constant satises Eulers equation. The helix is regular.

14 Multiply the nonlinear equation u

+sinu = 0 by v and integrate the rst

term by parts tond the weak form. Whatintegral P is minimized by u?
15 Find the Euler equations (strongform) for
1
2
u

2
u

2
u

2
(a) P(u)= +2 + dxdy
2 x
2
xy y
2
1
2
(b) P(u)= (yu
2
+u
y
)dxdy (c)E(u)= u 1+(u

)
2
dx
2
x
1
2 2
(d) P(u)= (u
2
+u
y
)dxdy with u dxdy=1.
2
x

c 2006Gilbert Strang
16 Show that the Euler equations forthese integrals are the same:

2
u
2
u
2
u

2
y
2
dxdy and dxdy
x
2
xy
Presumably the two integrals are equal if the boundary conditions are zero.
17 Sketchthegraphofp
2
/2m+mgu=constantintheupplane. Isitanellipse,
parabola,orhyperbola? Markthepointwheretheballreachesmaximumheight
and begins tofall.
18 Drawasecondspringandmasshangingfromtherst. Ifthemassesarem
1
,m
2
and the spring constants arec
1
,c
2
,the energy is
1
2
1
2
1 1
2
H =K+P = p
1
+ p
2
+ c
1
u
1
+ c
2
(u
2
u
1
)
2
.
2m
1
2m
2
2 2
Find the four Hamiltons equations H/p
i
=du
i
/dt,H/u
i
=dp
i
/dt, and
the matrix equation Mu

+Ku=0.
19 The Hamiltonianforapendulum (withu=)isH =p
2
/2m+mgl(1cosu).
Write out Hamiltons equations (22) and eliminate p to nd the equation of a
pendulum.
1 1
20 Verify that the energy
2
e
T
Ce and the complementary energy w
T
C
1
w are
2
T 1
conjugate. Asinequation(18),thismeansthat
1
w
T
C
1
w=max[e w
2
e
T
Ce].
2