A Guide To Using MATLAB in Statics

Using MATLAB in Statics
A Guide to Using MATLAB in

ECE210 Statics
Dhaval Shah, Robert Hinks and S. D. Rajan
Department of Civil Engineering
Arizona State University
Tempe, AZ 85287-5306
August 2000
TABLE OF CONTENTS
Chapter
Page
Introduction
Sample Problems and Further Exercises

2.1 Forces on a Particle
2.1.1 Problem 2.1.1 Forces on a barge
2.1.2 Problem 2.1.2 Crate on an inclined plane
2.1.3 Problem 2.1.3 Equilibrium of a suspended lamp
2.2 Rigid Bodies and Equivalent Force Systems
2.2.1 Problem 2.2.1 Automobile towing bar
2.2.2 Problem 2.2.2 Calculation of a torque
2.2.3 Problem 2.2.3 Calculation of resultant force and moment
2.3 Distributed Forces: Centroids and Center of Gravity
2.3.1 Problem 2.3.1 Centroid of a quadrant of ellipse
2.3.2 Problem 2.3.2 Centroid of a jetway
2.3.3 Problem 2.3.3 Equivalent force in an automobile
2.4 Equilibrium of Rigid Bodies
2.4.1 Problem 2.4.1 Overhanging roof
2.4.2 Problem 2.4.2 Tow truck mechanism
2.4.3 Problem 2.4.3 Folding platform
2.4.4 Problem 2.4.4 Power-line pole
2.5 Truss Analysis
2.5.1 Problem 2.5.1 Cantilevered truss analysis
2.5.2 Problem 2.5.2 Truss analysis of a jack support stand
2.5.3 Problem 2.5.3 Space frames supporting window
washing scaffold
2.5.4 Problem 2.5.4 Lever system
2.5.5 Problem 2.5.5 Plow mechanism
2.6 Beam and Frame Analysis
2.6.1 Problem 2.6.1 Airplane wing acting as a cantilevered beam
2.6.2 Problem 2.6.2 Computation of tension in cable segments
2.7 Friction
2.7.1 Problem 2.7.1 Block on an inclined plane
2.7.2 Problem 2.7.2 Leveling of refrigerator using a wedge
4
5
6
8
10
13
14
17
18
21
22
24
26
28
29
31
34
36
39
40
42
45
49
51
53
54
56
58
59
61
Chapter 1
Introduction
There is a class of engineering problems that requires numerical solution either because finding exact solutions
is tedious, or because exact solutions cannot be found. Computer programs are indispensable in finding
numerical solutions. A wide choice of options is available including traditional high-level programming
languages such as FORTRAN, C, C++ etc. MATLAB provides a different option. It is an integrated
environment where numerical computations can be carried out either using MATLAB commands, or using a
user-written program. Excellent references are available to study, understand and use the capabilities of
MATLAB. The reader is encouraged to use these references. An excellent list is available at the following web
site: http://www.mathworks.com/support/books/index.php3.
The Student Edition of MATLAB has several manuals and tutorials. One of them MATLAB: The Language of
Technical Computing (using_ml.pdf) provides a good starting point. The developers of MATLAB, Mathworks,
Inc. have an excellent web site (http://www.mathworks.com) where additional resources can be found. In addition,
there are several books available that combine numerical analysis and MATLAB.
In this guide we will take a look at solving problems in statics using custom MATLAB programs. In other
words, we will develop custom computer programs using the MATLAB programming language. These
programs are developed usually using the MATLAB editor, and the computer program is saved in one or more
.m files. All the problems are taken from the current textbook for ECE210 Engineering Mechanics: Statics by
R.W.Soutas-Little and D.J.Inman, a Prentice-Hall publication (ISBN: 0-13-769001-0).
The first step in this process is to understand the (statics) theory necessary to solve the problem. Second, one
must write an algorithm (a sequence of steps) that outlines how the problem input can be used along with the
theory to generate the required output. Third, these steps must be translated into correct MATLAB statements.
Inherent in these steps is the possibility of making logical errors (errors that are based on flawed theory) or
syntax errors (errors in translating the algorithmic steps into MATLAB statements). Each one of us must find
ways of debugging these errors.
As a starting point, become familiar with the MATLAB environment. Run a few simple examples that are
command driven. Later, develop a few simple programs in MATLAB to solve very simple problems whose
solution can be easily checked by hand. Once you have mastered this, you are ready to understand the examples
in this guide and solve the computer-based problems in the ECE210 text.
Chapter 2
Sample Problems and Further Exercises
The problems in this chapter follow the sequence in a standard statics text, and include problems from the
following topics.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Forces on a Particle
Rigid Bodies and Equivalent Force Systems
Distributed Forces: Centroids and Centers of Gravity
Equilibrium of Rigid Bodies
Truss Analysis
Beam and Frame Analysis
Friction
Each of these topics has two or more example problems that have been solved using MATLAB. Every problem
is usually divided into two parts (1) the MATLAB solution to the problem, and (2) suggested further
exercises. In (2), additional questions are posed and you are required to modify the .m file to find the numerical
(or, even symbolic) solution.
Note that the MATLAB solution is not unique. The computer statements can usually be structured in a variety
of ways. However, the answers in almost all cases, are unique.
2.1 Forces on a Particle

Three problems are solved in this section.
This Guides Problem
ID
Problem 2.1.1
Problem 2.1.2
Problem 2.1.3
Corresponding Problem from ECE210

Text
Problem 2.11 on page 39
Problem Title
Forces on a barge
Crate on an inclined plane
Equilibrium of a suspended lamp
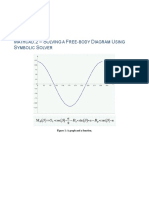
Problem 2.1.1 Forces on a barge
A barge is pulled by two tugboats as shown in the Figure P2.11. To move the
barge along in the water properly, the tugboats must exert a resultant force of
5000 lb along the direction of motion of the barge. First determine the tension in
each rope if the position of tug b is such that = 45. Second, suppose that tug b
can move anywhere such that 0 90 . Determine the angle at which
the angle in the Tug Bs rope is maximum, and again, at which the tension has
minimum value, still maintaining the resultant of 5000 lb along the x-direction.
o
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
1
2
3
4
5
6
7
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
LAST UPDATE: August 4, 2000
REFERENCE: Problem 2-11 on pg. 39 in Engineering Mechanics Statics by Soutas.
PROBLEM OVERVIEW: This problem deals with finding out the force "Tb" in the
rope between the tug B and the barge when the angle Beta
= 45 and the resultant force is 5000 lb. The second part of
the problem deals with finding out the maximum and minimum
force Tb while 'Beta' varies between 0 and 90 degrees.
CONCEPT KEYWORDS: Free-body diagrams, Equilibrium equations
VARIABLE DICTIONARY:
Variable
Remarks
Status
------------------Tb
Force in rope connecting barge to tug B
To be computed
Ta
Force in rope connecting barge to tug A
To be computed
Beta
Angle between horizontal and rope
connecting barge to tug B
Given
Alpha
Angle between horizontal and rope
connecting barge to tug A
Given
FResultant Resultant force
Given
AInc
Angular increment to be used with angle Beta
To be defined
TbMax
Max. force in rope to tug B
To be computed
AngleMax
Corresponding value of angle beta
To be computed
TbMin
Min. force in rope to tug B
To be computed
AngleMin
Corresponding value of angle beta
To be computed
---------------------------------------------------------------------------Set default values
FResultant = 5000;
Alpha = 30;
Beta = 45;
AInc = 10;
%
% Convert angles to radians
AngleToRadians = pi/180;
BetaR = Beta * AngleToRadians;
AlphaR = Alpha * AngleToRadians;

%
% ===== Part 1 of the problem ==================================================
% Write the two equations of equilibrium and eliminate Ta.
b = (sin(BetaR) * cos(AlphaR) / sin(AlphaR)) + cos(BetaR);
% Compute the force in rope from barge to tug B
Tb=FResultant/b;
% Display the result
fprintf('The force in the rope connecting barge to tug B is Tb=%g lb\n', Tb);
%
% ===== Part 2 of the problem ==================================================
% The angle beta will be varied between 0 and 90 degrees in increments of AInc
% degrees.
% We will store these values in a vector called AnglesV
% We will store the corresponding value of the force Tb in vector TbV
TbMin = 2*FResultant; TbMax = 0;
% Now loop through all possible values of beta
I = 0;
for Angle = 0:AInc:90
I = I + 1;
AnglesV(I) = Angle;
BetaR = AnglesV(I)*AngleToRadians;
b = (sin(BetaR) * cos(AlphaR) / sin(AlphaR)) + cos(BetaR);
% Compute the force in rope to tug B
TbV(I)= FResultant/b;
% Track the maximum value
if TbV(I) > TbMax
TbMax = TbV(I);
AngleMax = AnglesV(I);
end
% Track the minimum value
if TbV(I) < TbMin
TbMin = TbV(I);
AngleMin = AnglesV(I);
end
end
% Now we will plot the force in rope Tb versus the angle beta
plot (AnglesV, TbV);
grid;
xlabel ('Beta (degrees)');
ylabel ('Tb (lb)');
fprintf ('The minimum force in the rope is Tbmin = %g lb. at angle %g\n',...
TbMin, AngleMin);
fprintf ('The maximum force in the rope is Tbmax = %g lb. at angle %g\n',...
TbMax, AngleMax);
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Get a better answer for part 2 by changing the value of AInc.
What is your conclusion?
(2) Do the orientation of the maximum and minimum forces depend
on the resultant force?
Problem 2.1.2 Crate on an inclined plane

A 100-kg crate is held in equilibrium as it rests on a
frictionless inclined plane making an angle with the
horizontal (see Figure P2.106). (a) Compute the tension in the
cable T and the normal force at the surface for = 30 . (b)
Compute the tension in the cable T and the normal force at the
o
surface for at 5 increments, increasing from 0 to 90. Is

there some value of for which T = N?
o
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
----------------------------------------------------------------------------AUTHOR:
Dhaval Shah
%
%
%
%
%
%
%
%
%
%
%
%
%
CONCEPT KEYWORDS: Free-body diagrams, Equilibrium equations

PROBLEM OVERVIEW: This problem deals with finding out the tension in the cable
that holds the crate resting on an inclined surface at an
angle Theta with respect to the horizontal.
The second part of the problem deals with finding out the
tension in the cable for different values of Theta.
Variable
Remarks
-------------T
Force in cable connecting crate to wall
Theta Angle between inclined plane and horizontal
M
Mass of crate
W
Weight of crate
AInc
Angular increment to be used with angle theta
N
Normal Component of weight of crate
(90deg. to inclined plane)
g
Acceleration due to gravity = 9.81 m/s^2
Status
-----To be computed
Given
Given
To be computed
To be defined
To be computed
Given
% ------------------------------------------------------------------------------% Set default values:

Theta = 30;
M = 100;
g = 9.81;
W = M * g;
ThetaR = Theta*AngleToRadians;
AInc = 1;
% Using the equilibrium equations along the axis of the inclined plane:
T = W * sin(ThetaR);
% equation (A)
% Display results
fprintf('The force in the cable is T = %g N\n', T);
% Normal reaction
N = W * cos(ThetaR);
% equation (B)
fprintf('The normal force N = %g N\n', N);
%=====================part b===================================================
% Theta is now stored in a vector (ThetaV) with Theta varying from 0 to 90 degrees
% in increments of AInc.
% ThetaV is now a vector of 18 elements (with Ainc = 5) from 0 to 90.
ThetaV = (0:AInc:90);
% Reuse Eqns. (A) and (B) and store the force values in vector TV and NV
TV = W * sin(ThetaV * AngleToRadians);
NV = W * cos(ThetaV * AngleToRadians);
% Find for what value of Theta, T = N
AngleEquals = -1; TOL = 0.1;
I = 0;
I = I + 1;
% check whether the T and N are almost equal
if (abs(TV(I)-NV(I)) <= TOL)
AngleEquals = Angle;
break;
end
% check whether the (T-N) has changed sign
if ((Angle ~= 0 & Angle ~= 90) & (TV(I-1) <= NV(I-1) & TV(I) >= NV(I)))
AngleEquals = Angle;
break;
end
end
fprintf('The normal force N = T when theta=%g\n', AngleEquals);
% The plot function plots the different values of T against its corresponding
% value of Theta varying from 0 to 90 degrees.
plot (ThetaV, TV);
grid;
Xlabel ('Theta (degrees)');
Ylabel ('T (N)');
%
%
%
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) If the cable connecting the crate to the wall is replaced by a spring system
whose stiffness is known (say k=1000 N/m), what would be the displacement
in the spring?
(2) How would you solve the problem if the cable is not parallel to the inclined
plane but is at an angle of 20 degrees clockwise from the plane, i.e. the
point of attachment of the cable to the wall is 20 degrees higher than the
point of attachment of the cable to the crate?
Problem 2.1.3 Equilibrium of a suspended lamp

A 25-lb light fixture is suspended from a ceiling by four cords
attached at a point, with the geometry given in Figure P2.109.
(a) Assuming that gravity acts along the z-axis, calculate the
tension in the four cords. The dimensions are given in feet. (b)
Investigate the effect of the tensions in the cords of moving
the lamps to different heights by changing the z-coordinate of
the point where all the four cords meet from 5 ft to 10 ft and
then to 1 ft.
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
-----------------------------------------------------------------------------AUTHOR:
Dhaval Shah
REFERENCE:
Problem 2-110 on pg. 91 in Engineering Mechanics Statics by Soutas.
PROBLEM OVERVIEW: This problem deals with computing the tension in the 4 cords
that hold the lamp hanging vertically along the "z axis" from
the ceiling as a function of the connection point with respect
to the ceiling.
% CONCEPT KEYWORDS: Free-body diagrams, Equilibrium equations

%
% VARIABLE DICTIONARY:
% Variable
Remarks
% -------------% O
Point O is the origin
% Ax,Ay,Az
The x, y, z coordinates of point A
% Bx,By,Bz
The x, y, z coordinates of point B
% Cx,Cy,Cz
They are the x, y, z coordinates of point C
% T1,T2,T3,T4
Forces in cords AC,OC,BC,CL respectively
% Lzac,Lxac,Lyac Direction cosines of cord AC
% Lzoc,Lxoc,Lyoc Direction cosines of cord OC
% Lzbc,Lxbc,Lybc Direction cosines of cord BC
% Lac
Length of cord AC
% Loc
Length of cord OC
% Lbc
Length of cord BC
% W
Weight of lamp
Status
-----Given
Given
Given
Given
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
Given
10
%
%
%
HInc
T1Max, T2Max
T3Max
Height increment with Cz
To be defined
Max. force in cord T1, T2 and T3
To be computed
% --------------------------------------------------------------------------------% Set default values

W = 25; HInc = 1;
Ax = 0; Ay = 4; Az = 0;
Bx = 4; By = 0; Bz = 0;
Cx = 2; Cy = 1; Cz = 5;
Ox = 0; Oy = 0; Oz = 0;
% ============================ part (a) ===========================================
% Calculate the length of the cords
Lac = sqrt((Cx-Ax)^2 + (Cy-Ay)^2 + (Cz-Az)^2);
Lbc = sqrt((Cx-Bx)^2 + (Cy-By)^2 + (Cz-Bz)^2);
Loc = sqrt((Cx-Ox)^2 + (Cy-Oy)^2 + (Cz-Oz)^2);
% Calculate the direction cosines of cords
Lzac = (Cz-Az)/Lac; Lxac = (Cx-Ax)/Lac; Lyac = (Cy-Ay)/Lac;
Lzbc = (Cz-Bz)/Lbc; Lxbc = (Cx-Bx)/Lbc; Lybc = (Cy-By)/Lbc;
Lzoc = (Cz-Oz)/Loc; Lxoc = (Cx-Ox)/Loc; Lyoc = (Cy-Oy)/Loc;
%
%
%
%
Form the
T1lxac +
T1lyac +
T1lzac +
linear
T2lxoc
T2lyoc
T2lzoc
equations for the 3 unknowns T1, T2, T3

+ T3lxbc = 0.
+ T3lybc = 0.
+ T3lzbc = 25.
% Solving the above equations using [A][x]=[B]

A = [Lxac Lxoc Lxbc; Lyac Lyoc Lybc; Lzac Lzoc Lzbc];
B = [0;0;W];
x = inv(A)*B;
% Display results
fprintf ('The force in the cord AC is
fprintf ('The force in the cord OC is
fprintf ('The force in the cord BC is
% Calculate force in chord CL (T4)
T4 = W;
fprintf('The force in the cord CL is
T1 = %g lb\n', x(1));
T2 = %g lb\n', x(2));
T3 = %g lb\n', x(3));
T4 = %g lb\n', T4);
%=========================part (b) ==============================================

% Now loop through all possible values of Beta
I = 0; T1Max = 0; T2Max = 0; T3Max = 0;
for Height = 1.0:HInc:10
I = I + 1;
% We define the variable for the z coordinate of point C as a vector CzV
CzV(I) = Height;
Lac = sqrt((Cx-Ax)^2 + (Cy-Ay)^2 + (CzV(I)-Az)^2);
Lbc = sqrt((Cx-Bx)^2 + (Cy-By)^2 + (CzV(I)-Bz)^2);
Loc = sqrt((Cx-Ox)^2 + (Cy-Oy)^2 + (CzV(I)-Oz)^2);
% Calculate the direction cosines of
Lzac = (CzV(I)-Az)/Lac; Lxac =
Lzbc = (CzV(I)-Bz)/Lbc; Lxbc =
Lzoc = (CzV(I)-Oz)/Loc; Lxoc =
cords
(Cx-Ax)/Lac; Lyac = (Cy-Ay)/Lac;
(Cx-Bx)/Lbc; Lybc = (Cy-By)/Lbc;
(Cx-Ox)/Loc; Lyoc = (Cy-Oy)/Loc;
11
A = [Lxac Lxoc Lxbc; Lyac Lyoc Lybc; Lzac Lzoc Lzbc];

B = [0;0;W];
X = inv(A)*B;
% The tension in the cords are now stored in the vector for every values of Cz
% in the vector CzV
T1V(I) = X(1); T2V(I) = X(2); T3V(I) = X(3);
if (T1V(I) > T1Max) T1Max = T1V(I); end;
end
fprintf ('The max. force in cord AC is T1 = %g lb\n', T1Max);
fprintf ('The max. force in cord OC is T2 = %g lb\n', T2Max);
fprintf ('The max. force in cord BC is T3 = %g lb\n', T3Max);
% Plot the forces in the cords T1, T2, T3 for different heights at which the
% lamp hangs.
plot (CzV,T1V,'r'), hold on, text (CzV(2),T1V(2),'T1'),
plot (CzV,T2V,'b'), hold on, text (CzV(2),T2V(2),'T2'),
plot (CzV,T3V,'g'), text (CzV(2),T3V(2),'T3'), hold on,
grid on
xlabel ('Cz (ft)')
ylabel ('Forces (lb)')
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) What conclusion(s) can you draw from the graph?
(2) Does the change in length of one cord affect the forces in all the cords?
(3) When is the system in unstable equilibrium? Is this physically possible?
12
2.2 Rigid Bodies and Equivalent Force Systems

This Guides Problem
ID
Problem 2.2.1
Problem 2.2.2
Problem 2.2.3

Text
Problem Title
Automobile towing bar
Calculation of a torque
Calculation of resultant force and
moment
13
Problem 2.2.1 Automobile towing bar

Consider the automobile towing bar illustrated in Figure
P3.24. A 4000-N force is applied to the trailer hitch as
illustrated and causes the force to change through the angle
theta as the lead car pulls on the bar AB. Calculate the
moments about the bumper connection point B as a function
of the angle . Calculate the value of Mb at = 0,45, and
90 .
MATLAB File
%
% -----------------------------------------------------------------------------
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
AUTHOR:
LAST UPDATE:
REFERENCE:
Dhaval Shah
August 4, 2000
PROBLEM OVERVIEW: This problem deals with finding out the moment caused by a
4000 N force applied to the trailer hitch as a function
of the angle of application, Theta, of the 4000 N force.
CONCEPT KEYWORDS: Rigid Bodies, Equivalent Force Systems.
Variable
Remarks
-------------P
Force of 4000N applied at an angle Theta
Px
Component of force P along X axis
Py
Component of force P along X axis
C
Point of application of force P
B
Point about which the moment of force P is
required
M
Moment of Force P about point B
Lbc
Distance between points B and C
Alpha
Angle that Lbc makes with the Y axis
Theta
Angle at which the force is applied
Status
-----Given
To be computed
To be computed
Given
Given
To be computed
Given
Given
14
%
with respect to the X axis
Given
% Lx
Lever arm of the component of force P
%
along X axis
To be computed
% Ly
Lever arm of the component of force P
%
along Y axis
To be computed
% AInc
Angular increment to be used with angle Beta
To be defined
% -----------------------------------------------------------------------------------% Set default values
P = 4000;
Alpha = 60;
Lbc = 1;
AInc = 1;
Theta = 45;
%=============================part1==========================================
% Given
ThetaR = Theta*AngleToRadians;
Px = P*cos(ThetaR);
Py = P*sin(ThetaR);
% Calculate the lever arm of the force P components
AlphaR = Alpha*AngleToRadians;
Lx = Lbc * sin(AlphaR);
Ly = Lbc * cos(AlphaR);
% Calculate the moment about point B at theta = 45 degrees
M = Px * Ly - Py * Lx;
fprintf ('The moment about point B at theta 45 degrees is %g N-m\n',M);
%====================part 2=================================================
% Now loop through all possible values of Theta
I = 0; Index0=1; Index45=1; Index90=1;
% ThetaV is a vector holding values from 0 to 90 degrees, the MV is a
% moment vector of the same size as Theta and so are the components
% Px and Py of the force P.
I = I + 1;
ThetaV(I) = Angle;
Px = P*cos(ThetaV(I) * AngleToRadians);
Py = P*sin(ThetaV(I) * AngleToRadians);
MV(I) = Px * Ly - Py * Lx;
if (Angle == 0) Index0 = I; end;
end
% Plot the moment about point B for different values of theta
plot (ThetaV,MV)
text(ThetaV(Index0),MV(Index0),'M@0'),
text (ThetaV(Index90),MV(Index90),'M@90'),
text (ThetaV(Index45),MV(Index45),'M@45'),
grid on
xlabel ('Theta (degrees)');
ylabel ('Moment (N-m)');
% ==============================================================================
% FURTHER EXERCISES
15
% (1) What would be the forces acting at point A and B if the force P
%
acts at Theta = 0 degrees?
% (2) At what angle should the force be placed with the positive X
%
axis such that the moment about point A is 0?
16
Problem 2.2.2 Calculation of a torque

Given that
M o = 20i$ + 10 $j + 5k$ and F = 10i$ 10 $j 5k$ kN, where M o . F = 0 , calculate the value of the moment arm r that
will produce the given moment by application of the given force.

MATLAB File
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
1
2
3
4
5
6
7
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
PROBLEM OVERVIEW: This problem deals with computing a moment vector 'r'
required to produce a known moment by a known force.
CONCEPT KEYWORDS: Rigid Bodies, Varignon's Theorem
Variable
Remarks
Status
------------------Mx,My,Mz
Moment components
Given
Fx,Fy,Fz
Force components
Given
Rx,Ry,Rz
Components of relative position vector
To be computed
---------------------------------------------------------------------------Set default values
Define M = (Mx)i +
Define F = (Fx)i +
M(1) = 20; M(2) =
F(1) = 10; F(2) =
(My)j + (Mz)k
(Fy)j + (Fz)k
10; M(3) = 5;
-10; F(3) = -20;
% Let R = (Rx)i + (Ry)j + (Rz)k

% Varignon's theorem states M = R X F
% Using the process discussed in pages 124-126,
%
F X M
%
R = ----%
F . F
%
Numerator = cross (F, M);
Denominator = Dot (F, F);
R = Numerator/Denominator;
% Display results
fprintf ('The position vector R = (%g)i + (%g)j + (%g)k\n',...
R(1),R(2),R(3));
%
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) What magnitude of force is required to produce a moment vector of
M = 20i - 30k lb.ft for a position vector r = 3i + 2k.
(2) Given a force vector F = 2i + 3j, find out what would be the force
vector along a position vector r = 8j -3k.
17
Problem 2.2.3 Calculation of a resultant force and moment

Four forces act on a cross sectional piece of a truck frame (see
Figure P3.76). Calculate the resultant force and moment at
point A, and find a point B somewhere along the X-axis where
the resultant alone will represent the effect of all the four
forces. Here, let F1 = 10 kN , F2 = 10 kN , F3 = 3kN , and
F4 = 4 kN .
MATLAB File
%
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
% LAST UPDATE:
August 4, 2000
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%

PROBLEM OVERVIEW: This problem deals with computing a resultant force and moment
at point A for a given force system.
The next part of the problem is to find a point B on the x
axis where the resultant alone will represent all the forces.
CONCEPT KEYWORDS: Rigid Bodies: Varignon's Theorem

Variable
Remarks
-------------O
A()
The x, y coordinates of point A
B()
The x, y coordinates of point B
Status
-----Given
Given
To be computed
18
%
%
%
%
%
%
%
%
%
C()
D()
E()
F()
M()
Rda()
Rea()
Rca()
Roa()
The x, y coordinates of point C (F2)

The x, y coordinates of point D (F4)
The x, y coordinates of point E (F3)
Resultant Force vector about point A
Moment vector about point A
Relative position vector AD
Relative position vector EA
Relative position vector CA
Relative position vector OA
Given
Given
Given
Given
Given
Intermediate
Intermediate
Intermediate
Intermediate
qty.
qty.
qty.
qty.
% ---------------------------------------------------------------------------% (X, Y, Z) Coordinates of

A(1) = 0.3; A(2) = 0.3;
C(1) = 0.6; C(2) = 0;
D(1) = 0;
D(2) = 0.6;
E(1) = 0.6; E(2) = 0.6;
O(1) = 0;
O(2) = 0;
points
A(3) =
C(3) =
D(3) =
E(3) =
O(3) =
A, D, E, F, O
0;
0;
0;
0;
0;
% F1, F2, F3, F4 as vectors

F1(1)
F2(1)
F3(1)
F4(1)
=
=
=
=
0; F1(2) = 10; F1(3) = 0;

0; F2(2) = 10; F2(3) = 0;
-3; F3(2) = 0; F3(3) = 0;
4; F4(2) = 0; F4(3) = 0;
% Define Rd/a, Re/a, Rc/a, Ro/a

D = [D(1); D(2); D(3)];
E = [E(1); E(2); E(3)];
C = [C(1); C(2); C(3)];
A = [A(1); A(2); A(3)];
O = [O(1); O(2); O(3)];
Rda
Rea
Rca
Roa
=
=
=
=
D
E
C
O
A;
A;
A;
A;
% ================ calculation of moment=================================

% Moment of the above force vectors about point A involves cross-products
% M = Rd/a X F4 + Re/a X F3 + Rc/a X F2 + Ro/a X F1
M = cross (Rda, F4) + cross (Rea, F3) + cross (Rca, F2) + ...
cross (Roa, F1);
fprintf ('Vector M = [(%g)i + (%g)j + (%g)k] kN-m\n', M(1), M(2), M(3));
%================= calculation of resultant force F ========================
F = F1 + F2 + F3 + F4;
fprintf ('Vector F = [(%g)i + (%g)j + (%g)k] kN\n', F(1), F(2), F(3));
%============================ part b ======================================
% Given that point B lies on the X axis.
B(2) = 0; B(3) = 0; BINC = 0.01; TOL = 0.1;
% We can find Bx, i.e. B(1) by computing the moment about B using
%
M = Rd/b X F4 + Re/b X F3 + Rc/b X F2 + Ro/b X F1
% and then setting the z component of M to zero. This will give us an
% equation with Bx as the unknown. Solving ...
19
for BX = 0:BINC:0.6
B(1) = BX;
Rdb = D - B;
Reb = E - B;
Rcb = C - B;
Rob = O - B;
M = cross (Rdb, F4) + cross (Reb, F3) + cross (Rcb, F2) + ...
cross (Rob, F1);
if (abs(M(3)) < TOL)
fprintf ('The coordinates of point B are (%g, %g) m\n', B(1), B(2));
break;
end
end
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Calculate the resultant force and moment about point O.
(2) Compute a position vector from 'O' to 'A'. Use the resultant
force vector obtained above to compute a force vector along the
given position vector, Ro/a.
20
2.3 Distributed Forces: Centroids and Center of Gravity

This Guides Problem
ID
Problem 2.3.1
Problem 2.3.2
Problem 2.3.3

Text
Problem Title
Centroid of a quadrant of an ellipse
Centroid of a jetway
Equivalent force in an automobile
21
Problem 2.3.1 Centroid of a quadrant of ellipse

Calculate the centroid of the area found by the quadrant of an
ellipse (see Figure P4.15). The equation of an ellipse is
FG x IJ + FG y IJ
H aK H bK
2
=1
%0
1
2
3
4
5
6
7
% --------------------------------------------------------------------------% AUTHOR:
Dhaval Shah
% LAST UPDATE: August 4, 2000
%
% REFERENCE: Problem 4-15 on pg. 190 in Engineering Mechanics Statics by Soutas.
%
% PROBLEM OVERVIEW: This problem deals with computing the centroid of the area
%
formed by a quadrant of an ellipse whose equation is:
%
(x/a)^2 + (y/b)^2 = 1.
% CONCEPT KEYWORDS: Centroids of Areas by First Moment.

%
% Variable
Remarks
% -------------% O
% a
length on the major axis (X)
% b
length on the minor axis (Y)
% A
Area of the ellipse
% Xc
X coord. of centroid of the ellipse
% Yc
Y coord. of centroid of the ellipse
Status
-----Given
Given
Given
To be computed
To be computed
To be computed
% ----------------------------------------------------------------------------
%
%
%
%
%
To calculate the centroid of the ellipse, we first need to calculate

the area(A) as follows. Consider a vertical strip of infinitesimally
small thickness 'dx' at any 'x' having height of 'y'. Let the area of
this strip be dA = y.dx. As this strip moves along the x axis from '0'
to 'a', we need to integrate the above equation dA from '0' to 'a'.
% Defining the symbols to be used for integration.

syms a b theta
% We now change from the cartesian coordinate system to the polar coordinates
x = a*cos(theta);
y = b*sin(theta);
% Taking the derivative of the above equations to obtain the area A
dx = diff(x,theta);
22
dy = diff(y,theta);
% A = integral (xdy)
dA = x*dy;
A = int(dA,0,pi/2);
% To obtain the centroid of the given ellipse: Yc = [integral (ydA)]/A
% Xc = [integral (xdA1)]/A1
dA1 = y*dx;
A1 = int(dA1,0,pi/2);
cgy = y*dA;
cgx = x*dA1;
Yc = int(cgy,0,pi/2)/A;
Xc = int(cgx,0,pi/2)/A1;
% Display the results
fprintf('The Area formed by the quadrant of the ellipse is: ');pretty(A)
fprintf ('The X coordinate of the centroid is: '); pretty(Xc)
fprintf ('The Y coordinate of the centroid is: '); pretty(Yc)
%
%
%
%
%
%
FURTHER EXERCISES
(1) How would you modify the above program to obtain the area, and the centroid
of the semi ellipse.
(2) If we form a rectangle of dimension (a X b), then write a code to calculate
the area obtaind by deducting the quadrant of the ellipse from the rectangle.
(3) Solve the above problem for a special case when a = b.
23
Problem 2.3.2 Centroid of a jetway

The jetway leading to an aircraft is a telescopic device formed
by a series of interconnected rectangular parallelepiped. The
designer of this device needs to know where the center of
gravity is at each position as the jetway telescopes out along
the X-axis. The length of each rectangular parallelepiped is
20 ft , and the walls are 3in thick. The first section is
20 ft 10 ft 10 ft . Using the centreline coordinate system

illustrated in Figure P4.51, compute the position of the
centroid as the section extends from zero to 15 ft past the
edge of the first section.
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
PROBLEM OVERVIEW: To obtain the centre of gravity of the jetway leading to an
aircraft at each position as it telescopes out along the
x-axis. Given the length of each rectangular parallelepiped
is 20ft.and the walls are 3in. thick. The first section is
20ft X 10ft X 10ft
% CONCEPT KEYWORDS: Centroids, Composite bodies.

%
% Variable
Remarks
Status
% ------------------% L1, B1, H1 Length, breadth, height of the
%
first section
Given
% T
Wall Thickness
Given
% B2, H2
Breadth and height of telescopic
%
section
To be computed
% Lt
Length of the telescopic section
Given
% V1
Volume of first section
To be computed
% V2
Volume of telescoping section
To be computed
% X1, Y1, Z1 X,Y,Z coordinates of the centroid of
%
the first section
Given
% X2, Y2, Z2 X,Y,Z coordinates of the centroid of
%
telescoping section
To be computed
% X, Y, Z
X, Y, Z coordinates of the centroid
%
jetway
To be computed
% ----------------------------------------------------------------------------
24
% Set default values: Units feet.

L1 = 20;
B1 = 10;
H1 = 10;
T = 3/12;
AInc = 1;
% calculate the volume of the first section: V1 = V1outer - V1inner
V1outer = L1*B1*H1;
V1inner = L1*(B1-T)*(H1-T);
V1 = V1outer - V1inner;
% Define the X, Y, Z centroid of the first section
X1 = L1/2; Y1 = 0; Z1 = 0;
% Compute the breadth and the length of the telescopic section.
B2 = B1 - T;
H2 = H1 - T;
% Now run through the loop for different values of the length of the jetway.
I = 0;
for Lt = 0:AInc:15
I = I + 1;
% Volume of the (telescopic) second section
L2 = Lt;
V2outer = L2*B2*H2;
V2inner = L2*(B2-T)*(H2-T);
V2 = V2outer - V2inner;
X2 = 20 + (Lt/2);
% Compute the X, Y, Z coordinate of the centroid of the entire jetway
X(I) = (V1*X1 + V2*X2)/ (V1 + V2);
Lj(I) = Lt;
end
% Plot the X coordinate of the centroid of the entire section against the
% different values of the lengths of the jetway.
plot (Lj, X)
grid
Xlabel ('Length (ft)')
Ylabel ('Centroid (X) (ft)')
%
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Would the centroid of the entire section change, if the breadth and the height
of the parallelopiped is changed?
(2) If one of the walls of the parallelopiped is kept open such that the jetway is
is open on one of its sides, what would be the new centroid of the entire
section for Lj = 10ft?
25
Problem 2.3.3 Equivalent force in an automobile

A side-impact air bag for an automobile may be modeled as a distributed load by
equivalent force and point of action for this system. Use Figure P4-60.
w( x ) = 100(1 + cos( x )) lb ft . Compute the
MATLAB File
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
% LAST UPDATE:
August 4, 2000
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%

PROBLEM OVERVIEW: To compute the equivalent force and its point of action
for a system subjected to a distributed load by
w(x) = 100(1 + x*cos(x))
CONCEPT KEYWORDS: Centroid of Area, First Moment.
Variable
Remarks
Status
------------------W
Distributed load
Given
A
Area under the load curve
To be computed
Xc
X coord. of centroid of the distributed
load
To be computed
----------------------------------------------------------------------------
% Set absolute values:
26
a = 2;
wc = 100;
%
%
%
%
%
To calculate the centroid of the distributed load we need to calculate

the area, A. Consider a horizontal strip of infinitesimally small
thickness 'dx' at any 'x' having length of 'w(x)'. Let the area of this
strip be dA = dA = w(x)dx. As this strip moves along the x axis, we need
to integrate with the limits of integration from '0' to 'a'.
% Numerically integrate using Trapezoidal Rule

A = 0; xinc = 0.01;
for x = 0:xinc:a;
x1 = x + xinc;
A = A + 0.5 * xinc * wc * ((1 + x*cos(x)) + (1 + x1*cos(x1)));
end
% Display the results.
fprintf ('The equivalent force in %g lb\n', A);
% To obtain the centroid of the given load, Xc = [integral (xdA)]/A
Xc = 0; xinc = 0.01;
for x = 0:xinc:a;
x1 = x + xinc;
Xc = Xc + 0.5 * xinc * wc * (x*(1 + x*cos(x)) + ...
x1*(1 + x1*cos(x1)));
end
Xc = Xc/A;
fprintf ('The X coordinate of the centroid is %g ft\n', Xc);
% ==============================================================================
% FURTHER EXERCISES
% (1) What would be the desirable features of the distributed load?
27
2.4 Equilibrium of Rigid Bodies

Four problems are solved in this section.
This Guides Problem
ID
Problem 2.4.1
Problem 2.4.2
Problem 2.4.3
Problem 2.4.4

Text
Problem Title
Overhanging roof
Tow truck mechanism
Folding platform
Power-line pole
28
Problem 2.4.1 Overhanging roof

An overhanging roof for an outdoor caf consists of a beam 5
m long of mass 100 kg (See Figure P5.31). Consider designing
the support system. That is, choose where to attach the cable
(pick l ) so that the tension in the cable and the reaction force
at the pin are the smallest. Compute values of the reaction
forces for l = 0.5,115
, . ,....,5.
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
PROBLEM OVERVIEW: This problem deals with finding out an appropriate
the beam of mass 100kg to attach the cable so that
in the cable and the reaction force at the pin are
The cable is connected between point A on the wall
on the beam.
length on
the tension
the smallest.
and point B
CONCEPT KEYWORDS: Equilibrium, Rigid bodies.

Variable
Remarks
-------------T
Force in the cable
L
Length at which the cable needs to be attached
Theta
Angle between horizontal and the cable
h
Height between the pin connection on the wall
and point A (where cable is anchored).
M
Mass of the beam
AInc
Increment to be used with length l
TMin
Min. force in cable
MinStress
Min. stress in cable
Status
-----To be computed
To be computed
Given
Given
Given
To be defined
To be computed
To be computed
% ---------------------------------------------------------------------------% Set default values

h = 1;
M = 100;
AInc = 0.5;
g = 9.81;
W = M * g;
% Weight of the beam.
% ===== Part 1 of the problem ================================================
29
% Resolving the tension in the cable into its 2 components.

%
Th = T*cos(ThetaR);
%
Tv = T*sin(ThetaR);
% Taking moments about the hinge to obtain the value of Tv:
%
Tv X L = M X 2.5
%
Tv = 2.5M/L
% Now using the equilibrium equations along X and Y direction:
J = 1;
% array increment
for I = 0.5:AInc:5
% Length 'l' varying from 0.5 to 5 and stored in an array L
L(J) = I;
ThetaV(J) = atan(h/L(J));
Tv(J) = 2.5*W/(L(J));
% Vertical component of the tension
Rv(J) = W - Tv(J);
% Vertical component of reaction
% Compute the tension in the cable
T(J) = Tv(J) / sin(ThetaV(J));
% Tension in the cable.
Th(J) = T(J)*cos(ThetaV(J));
% Hor. component of the tension
Rh(J) = Th(J);
% Horizontal component of raction
R(J) = sqrt((Rv(J))^2 + (Rh(J))^2); % Reaction at the hinge
J = J + 1;
end
% Now we will plot the force in cable 'T' and reaction 'R' versus the length 'L'
plot (L, T),hold on, plot(L, R),
text (L(2),T(2),'Tension'), text(L(5),R(5),'Reaction')
grid, xlabel ('Length (m)')
ylabel ('T (N)')
% Obtain the minimum values of the tension and the reaction forces
TMin = min(T);
RMin = min(R);
for I = 1:1:J-1
if T(I) == TMin
LMin = L(I);
end
if R(I) == RMin
LRMin = L(I);
end
end
fprintf ('The minimum tension in the cable is Tmin=')
fprintf ('%g N at %g m from the pin\n', TMin, LMin);
fprintf ('The minimum reaction in the cable is Rmin=')
fprintf ('%g N at %g m from the pin\n', RMin, LRMin);
%
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Compute the minimum tension in the cable by varying the height 'h'
and keeping the length 'L' at 'LMin' obtained above.
(2) If the beam cross section varies such that for first 2.5m from the
hinge, the cross-sectional area is twice as much as the rest of the
beam, calculate the minimum tension in the beam for M = 100 kg, L = 4m.
30
Problem 2.4.2 Tow truck mechanism

Consider the tow truck mechanism of Figure P5.35, and calculate the value of the reaction
forces and the tension in the cable for values of from 0 to 60 in increments of 5 .
Incrementing in this manner corresponds to changing the position of the motor used to
hoist an object (usually an automobile) relative to the truck frame. Such information is
useful in the design of the hoist system. Is there a preferred position , where the
magnitude of the reaction force at A is a minimum?
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
PROBLEM OVERVIEW: This problem deals with computing the value of the reaction
forces and the tension in the cable for different values of
'Theta' from 0 to 60 degrees in increments of 5 degrees.
Calculate the value of 'Theta' at which the reaction is minimum.
Variable
Remarks
-------------T
Force in the supporting cable
Tac
Force in the hoist cable
Lac
Length at bar AC
Theta
Angle between hoist cable and the lift bar
AC
Beta
Angle between supporting cable and the
lift bar AC
Alpha
Angle between lift bar AC and horizontal
Rp, Rt
Reaction components at A
AInc
Increment to be used with angle Theta
TMin
Min. force in cable
Status
-----To be computed
To be computed
Given
Given
Given
Given
To be computed
To be defined
To be computed
31
W = 1500;
AInc = 5;
Lac = 8;
Beta = 20;
Alpha = 60;
BetaR = Beta * AngleToRadians;
AlphaR = Alpha * AngleToRadians;
% ===== Part 1 of the problem ================================================
% Force in the hoist cable is equal to the supported weight
Tac = W;
% Resolving the tension in the cable into its 2 components.
% Tacp is the component perpendicular to the lift bar and
% Tact is along the bar.
% Tt = Tac*cos(Theta);
% Tp = Tac*sin(Theta);
% Taking moments about point A, we can obtain T.
% T*sin(Beta) * (2/3)Lac = Lac*W*cos(Alpha) - Lac*Tp
(eqn. (A))
% Now using the equilibrium equations along X and Y direction:
% Angle Theta is varying from 5 to 60 and is stored in array ThetaV.
J = 0;
% array increment
for I = 0:AInc:60
J = J + 1;
ThetaX = I;
ThetaR(J) = ThetaX * AngleToRadians;
Tacp = Tac*sin(ThetaR(J));
Tact = Tac*cos(ThetaR(J));
% Using the equation(A) as shown above, we can compute the value of T
TX = (W*cos(AlphaR)*Lac - Tacp*Lac)/(sin(BetaR)*(2/3)*Lac);
% Ensure that cable is always in tension
if (TX < 0)
J = J-1;
break;
end;
T(J) = TX;
ThetaV(J) = ThetaX;
% Compute the two components of T (along and perpendicular to the bar)
Tt = T(J)* cos(BetaR);
Tp = T(J)* sin(BetaR);
% Compute the two components of reaction R at A
Rp(J) = W*cos(AlphaR) - Tacp - Tp;
Rt(J) = W*sin(AlphaR) + Tact + Tt;
% Compute the resultant
R(J) = sqrt((Rp(J))^2 + (Rt(J))^2);
end
% Now we will plot the force in cable 'T' and reaction 'R' versus the angle 'Theta'
plot (ThetaV, T),hold on, plot(ThetaV, R),
text (ThetaV(2),T(2),'Tension'), text(ThetaV(5),R(5),'Reaction'),
grid
xlabel ('Theta (degrees)')
ylabel ('T (lb)')
TMin = min(T);
RMin = min(R);
% Compute the angles at which the reaction and the tension in the cable are minimum
32
for I = 1:1:J
if T(I) == TMin
AngleMinT = ThetaV(I);
end
if R(I) == RMin
AngleMinR = ThetaV(I);
end
end
fprintf ('The minimum reaction at point A is Rmin=')
fprintf ('%g N when Theta = %g degrees\n', RMin, AngleMinR);
fprintf ('The minimum force in the cable is Tmin=');
fprintf ('%g N when Theta=%g degrees.\n', TMin, AngleMinT);
%
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Compute the minimum tension in the cable by varying the length of lift bar Ac
from 2ft to 10ft.
(2) If the supporting cable was connected at point C at one end and maintaining its
other end at hinge, compute the maximum tension in the cable for different values
'Theta' varying from 20 to 60 degrees.
33
Problem 2.4.3 Folding platform

A folding platform is used to hold parts, as well as to
conserve floor space when not in use. The platform is
supported by a hinge at C, which is assumed to support
negligible moments, a leg at B, modeled as a frictionless
support, and a removable pin at A, modeled as a
thrustless bearing, again with negligible moments. If the
platform is loaded as illustrated in Figure P5.73,
compute the reaction forces at A, B, and C. Ignore the
thickness of the platform.
MATLAB File
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
August 4, 2000
LAST UPDATE:

PROBLEM OVERVIEW: This problem deals with computing the value for the reaction
forces at points A, B, and C when a vertical force P
is applied at point D.
Variable
Remarks
---------------P
Applied vertical force (at D)
O
A,B,C,D
X,Y,Z coordinates of points A,B,C,D
Status
-----Given
Given
Given
34
% X
Reactions at A,B,C
To be computed
%==================================================================================
% Set default values
P(1) = 0;
P(2) = -3000;
A(1) = 0;
A(2) = 0;
B(1) = 1;
B(2) = 0;
C(1) = 0.5; C(2) = 0;
D(1) = 0.5; D(2) = 0;
Ra(1) = 0; Ra(2) = 1;
Rb(1) = 0; Rb(2) = 1;
Rc(1) = 1; Rc(2) = 1;
P(3) = 0;
A(3) = 1.2;
B(3) = 1.2;
C(3) = 0;
D(3) = 0.4;
Ra(3) = 1;
Rb(3) = 0;
Rc(3) = 1;
% There are six unknowns (Ray, Raz, Rby, Rcx, Rcy, Rcz)
% and six equations of equilibrium that we can write as
%
S X = Q
for i=1:1:6
Q(i) = 0;
for j=1:1:6
S(i,j) = 0;
end;
end;
% Force equilibrium equations
S(1,4) = 1;
S(2,1) = 1; S(2,3) = 1; S(2,5) = 1;
S(3,2) = 1; S(3,6) = 1;
% Take moments about the hinge C
S(4,1) = -1.2; S(4,3) = -1.2;
S(5,2) = 0.5;
S(6,1) = -0.5; S(6,3) = 0.5;
Rdc = D - C;
M = cross (Rdc, P);
% Generate the right-hand side vector
Q = [-P(1); -P(2); -P(3); -M(1); -M(2); -M(3)];
% Solve
X = inv(S)*Q;
fprintf ('The (y,z) reactions at point A are ');
fprintf ('%g N and %g N\n', X(1), X(2));
fprintf ('The (y) reaction at point B is ');
fprintf ('%g N\n', X(3));
fprintf ('The (x,y,z) reactions at point C are ');
fprintf ('%g N, %g N and %g N\n', X(4), X(5), X(6));
35
Problem 2.4.4 Power-line pole

In Figure P5.80, power-line pole is held in place by a
ball-and-socket connection at A, two cables at C and B,
and a rod at D. Ignoring the mass of the pole, compute
the reaction forces at A, B, C, and D for the load
indicated.
MATLAB File
%0
1
2
3
4
5
6
7
% -----------------------------------------------------------------------------% AUTHOR:
Dhaval Shah
%
%
% PROBLEM OVERVIEW: This problem deals with computing the tensions T1, T2, R
%
in order to compute the reaction forces at A, D, C and B.
% CONCEPT KEYWORDS: Free-body diagrams, Equilibrium
%
% Variable
Remarks
% -------------% O
% Ax,Ay,Az
The x, y, z coordinates of point
% Bx,By,Bz
% Cx,Cy,Cz
% Dx,Dy,Dz
% Ex,Ey,Ez
% Fx,Fy,Fz
equations
A
B
C
D
E
F
Status
-----Given
Given
Given
Given
Given
Given
Given
36
%
%
%
%
%
%
%
%
%
%
%
%
Gx,Gy,Gz
T1,T2,R
Lzcg,Lxcg,Lycg
Lzdf,Lxdf,Lydf
Lzbe,Lxbe,Lybe
Lgc
Ldf
Lbe
F
Rxa
Rya
Rza
The x, y, z coordinates of point G

Forces in cords DC,BE,DF respectively
Direction cosines of chord GC
Direction cosines of chord DF
Direction cosines of chord BE
Length of chord GC
Length of chord DF
Length of chord BE
Force applied
Reaction at point A along X axis
Reaction at point A along Y axis
Reaction at point A along Z axis
Given
To be
To be
To be
To be
To be
To be
To be
Given
To be
To be
To be
computed
computed
computed
computed
computed
computed
computed
computed
computed
computed
% --------------------------------------------------------------------------------% Set default values

FFx = -30; FFy =0; FFz = 0;
F = FFx;
Ax = 0; Ay = 0; Az = 0;
Bx = 0; By = 1; Bz = 10;
Cx = 0; Cy = -1; Cz = 10;
Dx = 0; Dy = 0; Dz = 7;
Ex = 3; Ey = 3; Ez = 0;
Fx = -2; Fy = 2; Fz = 0;
Gx = 3; Gy = 0; Gz = 0;
% ============================ part
% Calculate the length of the cords
Lgc = sqrt((Cx-Gx)^2 + (Cy-Gy)^2
Lbe = sqrt((Ex-Bx)^2 + (Ey-By)^2
Ldf = sqrt((Dx-Fx)^2 + (Dy-Fy)^2
(a) ===========================================
+ (Cz-Gz)^2);
+ (Ez-Bz)^2);
+ (Dz-Fz)^2);
% Calculate the direction cosines of cords

Lzcg = (-Cz+Gz)/Lgc; Lxcg = (-Cx+Gx)/Lgc; Lycg
Lzbe = (Ez-Bz)/Lbe; Lxbe = (Ex-Bx)/Lbe; Lybe =
Lzdf = (Dz-Fz)/Ldf; Lxdf = (Dx-Fx)/Ldf; Lydf =
% Form the equilibrium equations.
%
T1V = T1((Lxcg)i + (Lycg)j + (Lzcg)k))
%
T2V = T2((Lxbe)i + (Lybe)j + (Lzbe)k))
%
RV = R((Lxfd)i + (Lyfd)j + (Lzfd)k))
%
MaV = Rc/a X T1V + Rb/a X T2V + Rd/a X R
% Compute components of tension vectors T1V, T2V,
T1x = Lxcg; T1y = Lycg; T1z = Lzcg;
T2x = Lxbe; T2y = Lybe; T2z = Lzbe;
Rx = Lxdf; Ry = Lydf; Rz =Lzdf;
= (-Cy+Gy)/Lgc;
(Ey-By)/Lbe;
(Dy-Fy)/Ldf;
R:
% Compute relative position vector

Rcax = (Ax-Cx); Rcay = (Ay-Cy); Rcaz = (Az-Cz);
Rbax = (Ax-Bx); Rbay = (Ay-By); Rbaz = (Az-Bz);
Rdax = (Ax-Dx); Rday = (Ay-Dy); Rdaz = (Az-Dz);
% Define arrays for all position vectors and tensions T1, T2, R
Rca = [Rcax; Rcay; Rcaz]; Rba = [Rbax; Rbay; Rbaz];
Rda = [Rdax; Rday; Rdaz];
T1V = [T1x; T1y; T1z]; T2V = [T2x; T2y; T2z];
RV = [Rx; Ry; Rz];
% Compute components of MaV :M1
M1 = cross(Rca,T1V);
M2 = cross(Rba,T2V);
37
M3 = cross(Rda,RV);
% Compute the moments due to the given force F:
Rx = 0; Ry = 0; Rz = 10;
R = [Rx; Ry; Rz];
F = [Fx; Fy; Fz];
Mf = cross(R,F);
% Solve the linear equations [A][x] = [B]
% A = [ Ax Ay Az T1 T2 T3 ]
a = [1 0 0 Lxcg Lxbe Lxdf]; b = [0 1 0 Lycg Lybe Lydf];
c = [0 0 1 Lzcg Lzbe Lzdf]; d = [0 0 0 M1(1) M2(1) M2(1)];
e = [0 0 0 M1(2) M2(2) M3(2)]; f = [0 0 0 M1(3) M2(3) M3(3)];
A = [d;e;f;a;b;c];
B = [-Mf(1);-Mf(2);-Mf(3);-FFx;0;0];
X = inv(A)*B;
% Display results
fprintf('The reaction at A in x direction is Xa = %g\n',X(1));
fprintf('The reaction at A in x direction is Ya = %g\n',X(2));
fprintf('The reaction at A in x direction is Za = %g\n',X(3));
% FURTHER EXERCISES
% (1) Solve the above problem for F =50j + 20k.
% (2) If the connection at A is not a ball and socket type and if
%
Ma = 25i + 45j + 50k for F = 60i + 30K, calculate the tension in the
%
cables T1, T2, R.
38
2.5 Truss Analysis

Five problems are solved in this section.
This Guides Problem
ID
Problem 2.5.1
Problem 2.5.2
Problem 2.5.3

Text
Problem 2.5.4
Problem 2.5.5

Problem Title
Cantilevered truss analysis
Truss analysis of a joack support stand
Space frames supporting windowwashing scaffold
Lever system
Plow mechanism
39
Problem 2.5.1 Cantilevered truss analysis

Consider the cantilevered truss as sketched in Figure
P6.9, and calculate the forces in each member if a wind
load of approximately 1000 N is added at joint D. That
is, let L1 = 1000 N , L2 = 500 N , and L3 = 1000 N .
State which members are in tension and which are in
compression, and determine the reaction forces as well.
MATLAB File
%
%
%
%
%
%
%
%
%
%
-----------------------------------------------------------------------------AUTHOR:
Dhaval Shah
REFERENCE:
PROBLEM OVERVIEW: This problem deals with computing the internal forces in the
members and the reactions in the truss subjected to a wind load
of 1000KN at joint D. Given L2 = 500N and L1 = 1000N are the
forces acting joints C and E respectively.
% CONCEPT KEYWORDS: Free-body diagrams, Equilibrium equations

%
% Variable
Remarks
% -------------% L1,L2,L3
Forces applied at joints C, E, D
%
respectively
% Lac,Lab,Lcd,Lce
Lengths of different truss members
% Fac,Fab,Fcd,Fce
Forces in different truss members
% Fbc,Fdb,Fde
% Theta1
Angle between CE and DE
% Theta2
Angle between AC and BC
% Theta3
Angle between BC and BD
% Rxa
% Rya
% Rxb
Reaction at point B along X axis
% Ryb
Reaction at point B along Y axis
Status
-----To
To
To
To
To
To
To
To
To
To
To
be
be
be
be
be
be
be
be
be
be
be
computed
computed
computed
computed
computed
computed
computed
computed
computed
computed
computed
% --------------------------------------------------------------------------------% Set default values:

L1 = 1000;
L2 = 500;
L3 = 1000;
40
Lac = 1; Lce = 2; Lab = 1.5; Lcd = 1;

% Compute the angles :
Theta1 = atan(Lcd/Lce);
Theta2 = atan(Lab/Lac);
% Consider the equilibrium of joint E:
Fed = L2/sin(Theta1);
Fce = Fed*cos(Theta1);
% Consider the equilibrium of joint D:
Fdb = (Fed*cos(Theta1)+L3)/cos(Theta1);
Fcd = Fdb*sin(Theta1) - Fed*sin(Theta1);
% Consider the equilibrium of joint C:
Fcb = (L1 - Fcd)/sin(Theta2);
Fca = Fcb*cos(Theta2) + Fce;
% Consider the equilibrium of joint B:
Fba = Fcb*sin(Theta2) + Fdb*sin(Theta1);
% Compute the support reactions
Rax = Fca;
Ray = Fba;
Rbx = Fdb*cos(Theta1) + Fcb*cos(Theta2);
Rby = 0;
% Display results:
fprintf('The forces in members are: Fec = %gN(T)\nFed = %gN(C)\n',...
Fce, Fed);
fprintf('Fdc = %gN(C)\nFdb = %gN(C)\nFbc = %gN(C)\nFba = %gN(T)\n',...
Fcd, Fdb, Fcb, Fba);
fprintf('Fca = %gN(T)\n',Fca);
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Compute the force in member CD if the force L3 = 1000N.
(2) Vary the length of AB from 1 to 10ft and calculate the corresponding force in
member CD.
41
Problem 2.5.2 Truss analysis of a jack support stand

Suppose that you are asked to design the stand illustrated in
Figure P6.19 by choosing the angle that gives that gives the
smallest value of force in each member. A constraint on your
solution is that the stand must be 0.15 m high (that is, DB = 0.15
m) and that the width of the stand (as measured by the line AC)
must be less than 0.4 m. The maximum load the stand must hold
is 1500 N.
MATLAB File
% -----------------------------------------------------------------------------%
%
%
%
%
%
%
%
%
%
AUTHOR:
LAST UPDATE:
REFERENCE:
Dhaval Shah
August 4, 2000
PROBLEM OVERVIEW: This problem deals with computing the smallest value of force
in each member by choosing the angle 'Theta'.
Given that the stand BD must be 0.15m high and the width of the
stand AC must be less than 0.4 m. The maximum load on the stand
is 1500N.
% CONCEPT KEYWORDS: Free-body diagrams, Analysis of structures

%
% Variable
Remarks
% -------------% F
Applied load at joint B
% Lad, Ldc, Lbd
Lengths of different truss members
% Fad, Fab, Fbc, Fdc
% Theta
Angle between AD and AB
% Ha
% Va
% Vc
Reaction at point C along Y axis
Status
-----Given
Given
To be computed
To be computed
To be computed
To be computed
To be computed
% --------------------------------------------------------------------------------% Set default values:

F = 1500;
Lac = 0.2; Lcd = 0.1; Lad = 0.1; Lbd = 0.15;
AInc = 0.01;
RadiansToDegrees = 180/pi;
42
% Run through the loop for different values of Lad.

% We will assume that the stand is symmetric.
J = 0;
for I = 0.01:AInc:0.3
J = J + 1;
Lad(J) = I;
Lcd(J) = Lad(J);
% Compute Theta for differnt values of Lad
Beta(J) = atan(Lbd/Lcd(J));
Theta(J) = atan(Lbd/Lad(J));
end
% Compute the different forces in each member and reactions
% by using equilibrium equations
FTotalMin = 100*F;
for I = 1:1:J
% Compute vertical reaction at C
Vc = (F*Lad(I))/(Lad(I) + Lcd(I));
% Compute vertical reaction at A
Va = F - Vc;
Fab(I) = Va/sin(Theta(I));
% Apply equilibrium equations at A
Fbc(I) = Vc/sin(Beta(I));
% Apply equilibrium equations at B
Fdc(I) = Fbc(I)*cos(Beta(I));
% Apply equilibrium equations at C
Fad(I) = Fab(I)*cos(Theta(I));
% Apply equilibrium equations at D
Fdb(I) = 0;
FTotal = abs(Fab(I)) + abs(Fbc(I)) + ...
abs(Fdc(I)) + abs(Fad(I)) + abs(Fdb(I));
if (FTotal < FTotalMin)
FTotalMin = FTotal;
LMin = Lad(I);
ThetaMin = RadiansToDegrees*Theta(I);
end
% Convert from radians to degrees
ThetaD(I) = RadiansToDegrees*Theta(I);
end
fprintf ('Min force is for Lad=%g m or Theta=%g degrees\n',...
LMin, ThetaMin);
% Plot different forces in each member against Theta
plot (ThetaD,-Fab),text(ThetaD(2),-Fab(2),'Fab')
hold on,plot(ThetaD,-Fbc),text(ThetaD(4),-Fbc(4),'Fbc')
hold on,plot(ThetaD,Fdc),text(ThetaD(5),Fdc(5),'Fdc')
hold on,plot(ThetaD,Fdb),text(ThetaD(10),Fdb(10),'Fdb')
hold on,plot(ThetaD,Fad),text(ThetaD(10),Fad(7),'Fad')
grid on
xlabel ('Theta (degrees)');
ylabel ('Member Force (N)');
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Keeping the angle 'Theta' constant at 25 degrees, vary the height of
member DB between 0.1 m and 0.3 m and plot the forces in each member
against the height DB.
(2) Reformulate the design problem statement to obtain a more meaningful
43
design result.
44
Problem 2.5.3 Space frames supporting window-washing scaffold

A window-washing scaffold is supported by two space frames,
one of which is illustrated in Figure P6.60. The support at A is
a ball and socket, and those at B and C are frictionless
supports; C also has a pin restraint in the x-direction, to keep
the frame from rotating. Joint D is centered 1 m above the
intersection of BC and AE, which coincides with the midpoint
of line BC, which is 1 m long. (a) How many unknowns and
how many equations does this system represent if solved by
the method of joints? (b) Compute the reaction forces at points
and the forces in each member.
MATLAB File
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
--------------------------------------------------------------------------AUTHOR:
Dhaval Shah
PROBLEM OVERVIEW: This problem deals with computing a the reaction forces
and the force in each member of a window-washing
scaffold supported by 2 space trusses.
CONCEPT KEYWORDS: Analysis of Structures, Space Truss

Variable
Remarks
-------------O
Ax,Ay,Az
The x, y, z coordinates of point A
Bx,By,Bz
The x, y, z coordinates of point B
Dx,Dy,Dz
The x, y, z coordinates of point D
Ex,Ey,Ez
The x, y, z coordinates of point E
Cx,Cy,Cz
The x, y, z coordinates of point F
Fab,Fac,Fad Force vectors in members AB, AC, AD
Feb,Fec,Fed Force vectors in members EB, EC, ED
Fbc,Fbd,Fcd Force vectors in members BC, BD, CD
Nab,Nad,Nac Unit vectors along AB, AD, AC
Neb,Ned,Nec Unit vectors along EB, ED, EC
Nbc,Nbd,Ncd Unit vectors along BC, BD, CD
RBz
Reaction at B along Z axis
RCx
Reaction at C along X axis
RCz
Reaction at C along Z axis
RAx,RAy,RAz Reactions at A along X, Y, Z axis
Status
-----Given
Given
Given
Given
Given
Given
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
To be computed
% ----------------------------------------------------------------------------
45

F = 10;
Ax = 0; Ay = 0; Az = 0; Dx = 0.5; Dy = 0; Dz = 1; Ex = 2; Ey = 0; Ez =0;
Cx = 0.5; Cy = 0.5; Cz = 0; Bx = 0.5; By = -0.5; Bz = 0;
% Define M = (Mx)i + (My)j + (Mz)k
% Define F = (Fx)i + (Fy)j + (Fz)k
% Define R = (Rx)i + (Ry)j + (Rz)k
% Rd/a has 3 components : Rdax, Rday, Rdaz:
Rdax = (Dx - Ax); Rday = (Dy - Ay); Rdaz = (Dz - Az);
% Unit vector along Da:
Lda = sqrt(Rdax^2 + Rday^2 + Rdaz^2);
Ndax = Rdax/Lda; Nday = Rday/Lda; Ndaz = Rdaz/Lda;
% Rb/a has 3 components : Rbax, Rbay, Rbaz:
Rbax = (Bx - Ax); Rbay = (By - Ay); Rbaz = (Bz - Az);
% Unit vector along BA:
Lba = sqrt(Rbax^2 + Rbay^2 + Rbaz^2);
Nbax = Rbax/Lba; Nbay = Rbay/Lba; Nbaz = Rbaz/Lba;
% Rc/a has 3 components : Reax, Reay, Reaz:
Rcax = (Cx - Ax); Rcay = (Cy - Ay); Rcaz = (Cz - Az);
% Unit vector along CA:
Lca = sqrt(Rcax^2 + Rcay^2 + Rcaz^2);
Ncax = Rcax/Lca; Ncay = Rcay/Lca; Ncaz = Rcaz/Lca;
Rebx = (Ex - Bx); Reby = (Ey - By); Rebz = (Ez - Bz);
% Unit vector along EB:
Leb = sqrt(Rebx^2 + Reby^2 + Rebz^2);
Nebx = Rebx/Leb; Neby = Reby/Leb; Nebz = Rebz/Leb;
Recx = (Ex - Cx); Recy = (Ey - Cy); Recz = (Ez - Cz);
Lec = sqrt(Recx^2 + Recy^2 + Recz^2);
Necx = Recx/Lec; Necy = Recy/Lec; Necz = Recz/Lec;
Redx = (Ex - Dx); Redy = (Ey - Dy); Redz = (Ez - Dz);
Led = sqrt(Redx^2 + Redy^2 + Redz^2);
Nedx = Redx/Led; Nedy = Redy/Led; Nedz = Redz/Led;
Rbcx = (Bx - Cx); Rbcy = (By - Cy); Rbcz = (Bz - Cz);
% Unit vector along Da:
Lbc = sqrt(Rbcx^2 + Rbcy^2 + Rbcz^2);
Nbcx = Rbcx/Lbc; Nbcy = Rbcy/Lbc; Nbcz = Rbcz/Lbc;
Rbdx = (Bx - Dx); Rbdy = (By - Dy); Rbdz = (Bz - Dz);
Lbd = sqrt(Rbdx^2 + Rbdy^2 + Rbdz^2);
Nbdx = Rbdx/Lbd; Nbdy = Rbdy/Lbd; Nbdz = Rbdz/Lbd;
Rcdx = (Cx - Dx); Rcdy = (Cy - Dy); Rcdz = (Cz - Dz);
Lcd = sqrt(Rcdx^2 + Rcdy^2 + Rcdz^2);
Ncdx = Rcdx/Lcd; Ncdy = Rcdy/Lcd; Ncdz = Rcdz/Lcd;
%
%
%
%
%
Form the linear equations to determine the force in each member

and the reactions.
For joint A:
Ndax(AD) + Nbax(AB) + Ncax(AC) + Ax = 0;
Nday(AD) + Nbay(AB) + Ncay(AC) + Ay = 0;
46
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
Ndaz(AD) + Nbaz(AB) + Ncaz(AC) + Az = 0;

For joint B:
-Nbax(BA) + Nbex(BE) + -Nbcx(BC) + -Nbdx(BD) = 0;
-Nbay(BA) + Nbey(BE) + -Nbcy(BC) + -Nbdy(BD) = 0;
-Nbaz(BA) + Nbez(BE) + -Nbcz(BC) + -Nbdz(BD) + Bz = 0;
For joint C:
-Ncax(CA) + Ncex(CE) + Nbcx(CB) + -Ncdx(CD) + Cx = 0;
-Ncay(CA) + Ncey(CE) + -Nbcy(CB) + -Ncdy(CD) = 0;
-Ncaz(CA) + Ncez(CE) + -Nbcz(CB) + -Ncdz(BD) + Cz = 0;
For joint E:
-Nedx(ED) + -Nebx(EB) + -Necx(EC) = 0;
-Nedy(ED) + -Neby(EB) + -Necy(EC) = 0;
-Nedz(ED) + -Nebz(EB) + -Necz(EC) + -10 = 0;
For joint D:
-Ndax(DA) + Ndbx(BE) + Ndcx(BC) + -Nedx(BD) = 0;
-Nday(DA) + Ndbz(BE) + Ndcy(BC) + -Nedy(BD) = 0;
-Ndaz(DA) + Ndbz(BE) + Ndcz(BC) + -Nedz(BD) = 0;
% Solve for: [A][X] = [B]

% A = [ Fda Fba Fca Fed Fec Feb Fbc Fbd Fcd Ax Ay Az Cx Cz Bz]
a = [ Ndax Nbax Ncax 0 0 0 0 0 0 1 0 0 0 0 0 ];
b = [ Nday Nbay Ncay 0 0 0 0 0 0 0 1 0 0 0 0 ];
c = [ Ndaz Nbaz Ncaz 0 0 0 0 0 0 0 0 1 0 0 0 ];
d = [ 0 -Nbax 0 0 0 Nebx -Nbcx -Nbdx 0 0 0 0 0 0 0 ];
e = [ 0 -Nbay 0 0 0 Neby -Nbcy -Nbdy 0 0 0 0 0 0 0 ];
f = [ 0 -Nbaz 0 0 0 Nebz -Nbcz -Nbdz 0 0 0 0 0 0 1 ];
g = [ 0 0 -Ncax 0 Necx 0 Nbcx 0 -Ncdx 0 0 0 1 0 0 ];
h = [ 0 0 -Ncay 0 Necy 0 Nbcy 0 -Ncdy 0 0 0 0 0 0 ];
i = [ 0 0 -Ncaz 0 Necz 0 Nbcz 0 -Ncdz 0 0 0 0 1 0 ];
j = [ 0 0 0 -Nedx -Necx -Nebx 0 0 0 0 0 0 0 0 0 ];
k = [ 0 0 0 -Nedy -Necy -Neby 0 0 0 0 0 0 0 0 0 ];
l = [ 0 0 0 -Nedz -Necz -Nebz 0 0 0 0 0 0 0 0 0 ];
m = [-Ndax 0 0 Nedx 0 0 0 Nbdx Ncdx 0 0 0 0 0 0 ];
n = [-Nday 0 0 Nedy 0 0 0 Nbdy Ncdy 0 0 0 0 0 0 ];
o = [-Ndaz 0 0 Nedz 0 0 0 Nbdz Ncdz 0 0 0 0 0 0 ];
A = [ a; b; c; d; e; f; g; h; i; j; k; l; m ; n; o];
B = [ 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 10; 0; 0; 0];
x = inv(A)*B;
% Display results
fprintf ('Fda =
fprintf ('Fba =
fprintf ('Fca =
fprintf ('Fed =
fprintf ('Fec =
fprintf ('Fed =
fprintf ('Fbc =
fprintf ('Fbd =
fprintf ('Fcd =
fprintf ('RAx =
fprintf ('RAy =
fprintf ('RAz =
fprintf ('RCx =
fprintf ('RCz =
fprintf ('RBz =
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
%g
kN\n',x(1));
kN\n',x(2));
kN\n',x(3));
kN\n',x(4));
kN\n',x(5));
kN\n',x(6));
kN\n',x(7));
kN\n',x(8));
kN\n',x(9));
kN\n',x(10));
kN\n',x(11));
kN\n',x(12));
kN\n',x(13));
kN\n',x(14));
kN\n',x(15));
47
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Solve the above problem, if C has a pin restraint in the y-direction
instead of x-direction.
(2) Is the structure statically determinate if C has a pin restraint in both
x and y directions?
48
Problem 2.5.4 Lever system

Compute the forces at A, B, and C, as well as F, for the lever system of Figure P6.84 analytically in terms of the four lengths a, b, c,
and d.
MATLAB File
% ------------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
% LAST UPDATE:
August 4, 2000

%
% PROBLEM OVERVIEW: This problem deals with computing the forces at A, B, and C,
%
as well as F, for the lever system in terms of P, a, b, c,
%
and d. Point 'D' is the point where 'P' is applied and 'E'
%
is the point where 'F' is applied.
% CONCEPT KEYWORDS: Analysis of Structures: Free Body Diagrams
%
% Variable
Remarks
% -------------% F
Unknown force applied at E
% Lad, Lac, Lbc, Lbe
Distances on the beam
% P
Force applied at 'D'
% Vb
Reaction at point B along X axis
% Va
% Vc
Reaction at point C along Y axis
Status
-----To be computed
Given
Given
To be computed
To be computed
To be computed
% --------------------------------------------------------------------------------% Define variables or parameters that are to needed to compute the unknown quantities
syms a b c d F P
49
% Take moments about

Va = (P*(c+d))/d;
Vc = (P*c)/d;
F = (Vc*a)/(b);
Vb = (F*(b+a))/a;
point 'C' to compute Va

point 'A' to compute Vc
point 'B' to compute F
point 'C' to compute Vb
% Display results:
fprintf('The reactions at the joints are:\n');
fprintf('Va:'); pretty(Va)
fprintf('Vb:'); pretty(Vb)
fprintf('Vc:'); pretty(Vc)
fprintf('The force F = '); pretty(F)
50
Problem 2.5.5 Plow Mechanism

Compute the forces at the connections labeled for the plow mechanism in Figure P6.95, under the assumption that the blade of the
plow provides a force of P = 10 kN and W = 1.5 kN. Neglect the weight of the other members of the machine.
MATLAB File
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah

%
%
% PROBLEM OVERVIEW: This problem deals with computing the forces at the connections
%
for the plow mechanism, when the blade of plow provides a
%
force of P = 10kN and W = 1.5kN. Also, note that DE, BF
%
and GF are two force members.
%
% CONCEPT KEYWORDS: Analysis of Structures, Free Body Diagrams
%
% Variable
Remarks
Status
% ------------------% P, W
Forces that the blade provides
Given
% Fde,Fbf,Fgf
Forces in members DE, BF, GF
To be computed
% Ax,Ay
Reaction at A along X, Y axis
To be computed
51
% Fx,Fy
Reaction at F along X, Y axis
To be computed
% Cx,Cy
Reaction at C along X, Y axis
To be computed
% ---------------------------------------------------------------------------% Set default values:
P = 10; W = 1.5;
% From the geometry of figure, the angle CF makes with the horizontal is:
Alpha = atan(0.1/0.3);
%
%
%
%
The equilibrium equations for the blade portion are:

Summation Fx = Ax + 10 + Fgf*cos(alpha) = 0.
Summation Fy = Ay - 1.5 + Fgf*sin(alpha) = 0.
Summation Ma = W(0.05) - P(0.15) - Fgfcos(alpha)(0.3) = 0.
Fgf = (W*(0.05) - P*(0.15))/(0.3*cos(Alpha));
Ay = W - Fgf*sin(Alpha);
Ax = -P - Fgf*cos(Alpha);
% The angle that ED makes with the horizontal is 'Beta':

Beta = atan(0.2/0.3);
%
%
%
%
%
%
%
%
%
%
%
%
%
%
Consider the equilibrium of the body 'FDC'. Forces 'Fx', 'Fy' are the pin
forces acting at 'F'. Fde acts at 'D' at an angle 'Beta'. 'Cx', 'Cy' are the
the pin forces at 'C'.
Sum Fx = Cx - Fx + Fdecos(Beta) = 0
....(A)
Sum Fy = Cy + Fy - Fdesin(Beta) = 0
....(B)
Md = Cy(0.05) + Cx(0.2) - Fy(0.45) = 0
....(C)
The angle that FB makes with the horizontal is 'Theta':
Theta = atan(0.3/0.1);
Consider the equilibrium of the bar 'AFE'. Forces 'Fx', 'Fy' are the pin
forces acting at 'F'. Fde acts at 'E' at an angle 'Beta'. Ffb acts at
'F' at an angle 'Theta'.
Sum Fx = Fx - Fdecos(Beta) - Fgfcos(Alpha) - Fbfcos(Theta) - Ax = 0 ...(D)
Sum Fy = -Fy + Fdesin(Beta) - Fgfsin(Alpha) + Fbfsin(Theta) - Ay = 0 ...(E)
Mf = Fdesin(Beta)(0.2) + Fdecos(Beta)(0.2) + Ay(0.3) - Ax(0.4) = 0
From Mf = 0, we get:
Fde = (Ax*(0.4) - Ay*(0.3))/(sin(Beta)*0.2 + cos(Beta)*0.2);
% Now we solve a set of linear equations 'A' to 'E' described above

% to solve for Cx, Cy, Fx, Fy, Fbf.
% A = [ Cx Cy Fx Fy Fbf ]
a = [ 1 0 -1 0 0]; b = [ 0 1 0 1 0]; c =[ 0.2 0.05 0 -0.45 0];
d = [ 0 0 1 0 -cos(Theta)]; e = [ 0 0 0 -1 sin(Theta)];
f = Fgf*cos(Alpha)+Fde*cos(Beta)+Ax;
g = Fgf*sin(Alpha)-Fde*sin(Beta)+Ay;
A = [ a; b; c; d; e];
B = [ -Fde*cos(Beta); Fde*sin(Beta); 0; f; g];
x = inv(A)*B;
% Display results:
fprintf('The reactions
fprintf('The force Fde
fprintf('The force Fgf
fprintf('The force Fbf
at A
= %g
= %g
at C
at F
= %g
are Ax
kN\n',
kN\n',
are Cx
are Fx
kN\n',
= %g kN, Ay = %g kN\n', Ax,Ay);

Fde);
Fgf);
= %g kN, Cy = %gkN\n', x(1),x(2));
= %g kN, Fy = %gkN\n', x(3),x(4));
x(5));
52
2.6 Beam and Frame Analysis

Two problems are solved in this section.
This Guides Problem
ID
Problem 2.6.1

Text
Problem 2.6.2
Problem Title
Airplane wing acting as a cantilevered
beam
Computations of tension in cable
segments
53
Problem 2.6.1 Airplane wing acting a cantilevered beam

A lifting load on an airplane wing is modeled by
w( x ) = 1000 x sin( x )lb / ft , and the wing is modeled as a
10-ft-long cantilevered beam. (See Figure P7.31). Compute
the reaction forces, as well as the shear force and the bending
moment as a function of x. Plot the shear and the bending
moment functions.
MATLAB File: This is the main m-file which calls FV731.m and FB731.m files to plot the shear and bending functions.
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
August 4, 2000
LAST UPDATE:

PROBLEM OVERVIEW: To compute the reaction forces and the internal shear force
and bending moment. Plot the SF and BM as a function of 'x'.
The loading is w(x) = 1000*x*sin(x) lb/ft.
CONCEPT KEYWORDS: Shear Force, Bending Moments, Beams
Variable
Remarks
Status
------------------w
Distributed load
Given
A
Area under the load curve
To be computed
L
Length of the beam
Given
AInc
Increments to change the length'L' Given
----------------------------------------------------------------------------

L = 10;
w = 1000;
AInc = 0.1;
%
%
%
%
%
%
To calculate the total force acting on the beam we need to integrate the
distributed load w(x) along the length of the beam. The total load is the
area under the curve of the load w(x). Consider a vertical strip of
infinitesimally small thickness 'dx' at any 'x' having length of 'w(x)'.
Let the area of this strip be dA = w(x)dx. As this strip moves along
the x axis from '0' to 'L', we need to integrate the above equation dA
54
% from '0' to 'L'.

x=0:0.1:10;
n = length(x);
% Defines the length of the array 'x'
% Use the quad8 function for numerical integration

for i = 1:n
Vx(i) = quad8 ('fV731',0,x(i),[],[],w,L);
Mx(i) = quad8 ('fB731',0,x(i),[],[],w,L);
end
% prepare for plotting
figure(1); clf;
subplot (2,1,1)
plot (x,Vx)
% Plots shear force diagram
xlabel ('x (ft)')
ylabel ('V(x) (lb)')
subplot (2,1,2)
plot (x,Mx)
% Plots bending moment diagram
xlabel ('x (ft)')
ylabel ('M(x) (lb-ft)')
% ==============================================================================
% FURTHER EXERCISES
% (1) Solve the same problem by taking a vertical strip moving along the w(x) axis.
MATLAB File fV731.m

function y = fV731 (u,w,L)
% define the shear force function
y = w*(sin(u) - u.*sin(u)) - 7850;
MATLAB File fB731.m
function y = fB731(u,w,L)
% define the bending moment function
y = 71349 - 7850*u - 2000*cos(u) - 1000*u.*sin(u);
55
Problem 2.6.2 Computation of tension in cable segments

Compute the tension in each cable segment and the angles , ,
and for the traffic light system shown in Figure P7.59. Design
(choose) the hanger length l so that the top of the two lights hang
to the same level for ease of viewing. The length of the cable is
155 ft. Here, P1 = 125lb and P2 = 100lb .
MATLAB FILE: This is the main m-file. The equations are defined in m- file sp759_fcn.m and the nonlinear equation solver is in
file mnewt.m.
% ---------------------------------------------------------------------------
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
AUTHOR:
LAST UPDATE:
Dhaval Shah
August 4, 2000

PROBLEM OVERVIEW: To compute the tension in each cable segment and the angles
alpha, beta, and gamma for the traffic light system. Given that
P1 = 125lb and P2 = 100lb hang from B and C as shown in the
figure.
CONCEPT KEYWORDS: Internal Forces, Cables.
Variable
Remarks
Status
------------------L
Length of Cable
Given
P1, P2
Loads on the cable
Given
alpha1
Angle made by cable AB with horz.
To be computed
alpha2
Angle made by cable BC with horz.
To be computed
alpha3
Angle made by cable CD with horz.
To be computed
T1, T2, T3
Tensions in cables AB, BC, CD
To be computed
ABx, BCx
Horizontal lengths of AB, BC
Given
CDx, ADy
Lengths of CD, AD as shown in figure Given
---------------------------------------------------------------------------Set default values:
L = 155;
P1 = 125; P2 = 100;
ABx = 100; BCx = 25; CDx = 25; ADy = 0;
56
% put initial guesses into a column vector

%
T1
T2
T3
alpha1
alpha2
IC = [400; 400; 400;
5;
15;
alpha3
25];
% Use the Newton-Raphson method mnewt to solve the system

% on nonlinear equations
soln = mnewt('sp759_fcn', 100, IC, 1.0e-4, 1.0e-4, L, P1, P2,...
ABx,BCx,CDx,ADy);
fprintf('\nFor L =
fprintf('T1
fprintf('T2
fprintf('T3
fprintf('alpha
fprintf('beta
fprintf('gamma
%g ft the solution is\n', L);

= %8.3f lb\n', soln(1));
= %8.3f lb\n', soln(2));
= %8.3f lb\n', soln(3));
= %8.3f lb\n', soln(4));
= %8.3f lb\n', soln(5));
= %8.3f lb\n', soln(6));
MATLAB File sp759_fcn.m

function q = sp759_fcn (p, L, P1, P2, ABx, BCx, CDx, ADy)
% set up the equilibrium equations
T1 = p(1); T2 = p(2); T3 = p(3);
DegreesToRadians = pi/180;
alpha1 = p(4)*DegreesToRadians;
q = zeros(6,1);
q(1) = -T1*cos(alpha1) + T2*cos(alpha2);
q(2) = -T1*sin(alpha1) + T2*sin(alpha2) - P1;
q(3) = -T2*cos(alpha2) + T3*cos(alpha3);
q(4) = -T2*sin(alpha2) + T3*sin(alpha3) - P2;
q(5) = ABx*tan(alpha1) + BCx*tan(alpha2) + CDx*tan(alpha3) - ADy;
q(6) = sum([ABx BCx CDx]./cos([alpha1 alpha2 alpha3])) - L;
57
2.7 Friction
Two problems are solved in this section.
This Guides Problem
ID
Problem 2.7.1
Problem 2.7.2

Text
Problem Title
Wedge on an inclined plane
Leveling of a refrigerator by using a
wedge
58
Problem 2.7.1 Wedge on an inclined plane

A 10-lb force is pushing a 40-lb block, as shown in Figure P8.4.
The angle of inclination of the plane is which varies from 0
to 65 in increments of 5 . The coefficient of static friction

between the block and the incline is s = 0.75 , and the
coefficient of kinetic friction is k = 0.65 . Will the block slide
on the plane? If it does, will it slide up or down the plane? What
is the friction force between the block and the plane?
MATLAB File
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
August 4, 2000
LAST UPDATE:

PROBLEM OVERVIEW: This problem deals with finding out if the block of 40lb,
subjected to a horizontal force of 10lb, starts sliding on
an inclined plane making an angle 'Beta'?
CONCEPT KEYWORDS: Friction: Coulomb Friction.
Variable
Remarks
-------------W
Weight of the block
P
Force applied to the block
Beta
Angle of inclination of the
inclined plane
Status
-----Given
Given
To be varied
% Nus
Coefficient of Static Friction
Given
% Nuk
Coefficient of Kinetic Friction
Given
% Fs
Static frictional force
To be computed
% Fk
Kinetic frictional force
To be computed
% N
Normal force perpendicular to
%
the inclined plane
Intermediate qty
% AInc
Increments to change the angle 'Beta'
Given
W = 40;
P = 10;
Nus = 0.75; Nuk = 0.65;
AInc = 5;
AngletoRadians = pi/180;
59
% Now run through the for loop to get the different values of Beta
% from 0 to 65 degrees.
J = 0;
for I = 0:5:65
J = J + 1;
Beta(J) = I;
BetaR(J) = I * AngletoRadians;
% Define equilbrium equations to obtain the unknowns.
% Components perpendicular to the inclined plane are equated.
N = W*cos(BetaR(J));
Fs = Nus * N;
% Components along the plane are equated.
Fact = (W*sin(BetaR(J)) + P);
if Fs < Fact
fprintf ('The block will slide for angle %g degrees.\n',...
Beta(J));
Fk = Nuk * N;
fprintf ('Now that the block slides, the frictional');
fprintf (' force is %g lb\n', Fk);
else
fprintf (' The block will not slide for angle %g degrees.\n',...
Beta(J));
end
end
%
%
%
%
%
%
==============================================================================
FURTHER EXERCISES
(1) Resolve the above problem if the force P as shown in the figure is at an
inclination of 20 degrees with the inclined plane.
(2) Compute the force P in the above problem such that the block stays at rest
for all the cases of Beta varying from 0 to 65 degrees.
60
Problem 2.7.2 Leveling of a refrigerator by using a wedge

It is necessary to level the refrigerator shown in the Figure P8.87
with a 10 wedge system. The weight distribution is such that the

weights on all feet of the 800-lb refrigerator are equal. The
coefficient of friction between the feet and the contacting surface
is 0.8, the coefficient of static friction between the wedges is 0.2,
and the coefficient of static friction between the wedge and the
floor is 0.4. What is the minimum force P required to initiate
leveling of the refrigerator?
MATLAB FILE:
% ---------------------------------------------------------------------------
% AUTHOR:
Dhaval Shah
% LAST UPDATE:
August 4, 2000
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%
%

PROBLEM OVERVIEW: This problem deals with computing the minimum force P that
is applied to the wedge to level the refrigerator. Given that
the wedge system is 10 degrees and the coefficient of friction
between wedges is 0.2, between the feet and wedge is 0.8 and
that between the wedge and the floor is 0.8.
CONCEPT KEYWORDS: Friction, Coulomb Friction.
Variable
Remarks
-------------W
Weight of the refrigerator
P
Force applied to the wedge
Beta
Angle of inclination of the
wedge with horizontal
Nus1, Nus2, Nus3 Coefficient of Static Friction
Fs1
Frictional force between
feet and wedge
Fs2
Frictional force between two wedges
Fs3
Frictional force between
wedge and floor
Status
-----Given
To be computed
Given
Given
To be computed
To be computed
To be computed
61
% N
Normal force perpendicular to
%
the inclined plane of the wedge
Intermediate qty
% ---------------------------------------------------------------------------% Set absolute values:
W = 800;
W1 = W/4;
% weight on each foot of the refrigerator
Nus1 = 0.8; Nus2 = 0.2; Nus3 = 0.4;
Beta = 10;
AngletoRadians = pi/180;
BetaR = Beta * AngletoRadians;
% Consider the foot of the refrigerator in equilibrium and compute the force
% normal to its foot
N1 = W1;
% Compute the frictional force
Fs1 = N1*Nus1;
% Consider the equilibrium of the wedge on which 'P' is applied.
% Equating all the forces along the vertical:
N2 = W1/(cos(BetaR) - Nus2*sin(BetaR));
% Equating all the forces along the horizontal:
Fs2 = Nus2*N2;
P = Fs1 + N2*sin(BetaR) + Fs2*cos(BetaR);
% Display results:
fprintf ('The minimum force P required to level the refrigerator');
fprintf (' is: %g lb\n', P);
% ==============================================================================
% FURTHER EXERCISES
% (1) Solve the above problem for Beta = 5 degrees.
62

A Guide To Using MATLAB in Statics

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

A Guide To Using MATLAB in Statics

Uploaded by

Copyright:

Available Formats

Using MATLAB in Statics