Professional Documents
Culture Documents
Calculul Alfa Critic
Calculul Alfa Critic
Uploaded by
András TóthCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Calculul Alfa Critic
Calculul Alfa Critic
Uploaded by
András TóthCopyright:
Available Formats
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
Example: Calculation of alpha-cr
This worked example on the calculation of alpha-cr demonstrates for a
simple structure how the checks are performed. It shows whether second
order effects have to be taken into account or may be neglected for the
structural analysis.
IPE 400
HEB
200
IPE 400
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
HEB
200
HEB
200
3,50
IPE 400
HEB
200
3,50
HEB
200
IPE 400
HEB
200
6,00
6,00
3,00
3,00
Layout a) Rigid column bases
Layout b) Pinned column bases
Basic data
Check whether second order effects have to be taken into account or not.
Span length :
6,00 m
Bay width :
3,00 m
Slab depth :
12 cm
Partitions :
1,50 kN/m2
Imposed load :
5,00 kN/m2 (office building)
Concrete density :
24 kN/m3
Steel grade :
S235
Weight of the slab : 0,12 24 kN/m3 = 2,88 kN/m2
[m]
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Beams IPE 400 Steel grade S235
h = 400 mm
Width
b = 180 mm
Web thickness
tw = 8,6 mm
Flange thickness
tf = 13,5 mm
Fillet
r = 21 mm
Mass
66,3 kg/m
Section area
A = 84,46 cm2
of
Euronorm
tf
Depth
Sheet
19-57
tw
y
y
h
z
b
Second moment of area /yy Iy = 23130 cm4
Euronorm
Depth
h = 200 mm
Width
b = 200 mm
Web thickness
tw = 9,0 mm
Flange thickness
tf = 15,0 mm
Fillet
r = 18 mm
Mass
61,3 kg/m
Section area
A = 78,08 cm2
53-62
Second moment of area /yy Iy = 5696 cm4
Self weight of the beam :
(66,3 9,81) 10-3 = 0,650 kN/m
Permanent load :
G = 0,650 + (2,88 + 1,5) 3,00
3,50
= 13,79 kN/m
Variable load (Imposed load) :
Q = 5,0 3,0 = 15,0 kN/m
w1 = 2,03 kN/m
w2 = 0,76 kN/m
3,50
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Columns HE 200 B Steel grade S235
6,00
6,00
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
EN 1990
6.4.3.2
(6.10)
ULS Combination (simple):
G G + Q Q = 1,35 13,79 + 1,50 15,0 = 38,9 kN/m
w1 = 1,35 2,03 = 2,75 kN/m
w2 = 1,35 0,76 = 1,01 kN/m
EN 1993-1-1
Yield strength
Steel grade S235
Table 3.1
2
The maximum thickness is 15,0 mm < 40 mm, so : fy = 235 N/mm
Note :
The National Annex may impose either the values of fy from the
Table 3.1 or the values from the product standard.
EN 1993-1-1
5.3.2
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Global initial imperfections:
= 0 m h
Where: 0
is the basic value: 0 = 1/200
is the reduction factor for height h applicable to columns:
h =
2
h 1, 0
3
but
is the height of the structure in meters
is the reduction factor for the number of columns in a row:
m = 0,5 1 +
m
is the number of columns in a row including only those
columns which carry a vertical load NEd not less than 50% of
the average value of the column in the vertical plane
considered
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
Average compression force for the column:
-
1
N average = 38,9 12 2 = 311, 2 kN
3
-98,6
N Ed > 0 , 5 N average = 155 , 6 kN
-267,4
-198,8
-100,7
-525,9
-208,9
[kN]
from computer calculation
due to the internal force distribution (cp. computer calculation) three
columns should be considered (m = 3)
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
m = 0,5 (1 +
1
1
) = 0,5 (1 + ) = 0,816
m
3
h = 7,00 m
h =
=
2
7
= 0 , 756
1
1
0 , 756 0,816 =
200
324
Equivalent horizontal loads
H 1,d = H 2,d = g l =
1
38,9 12 = 1, 44 kN
324
Effects of deformed geometry of the structure
Calculation of cr
First order analysis may be used for the structure, if the increase of the
relevant internal forces or moments or any other change of structural
behaviour caused by deformations can be neglected. This condition may be
assumed to be fulfilled, if the following criterion is satisfied:
cr =
Fcr
10 (for elastic analysis)
FEd
cr =
Fcr
15 (for plastic analysis)
FEd
EN 1993-1-1
5.2.1 (3)
Example: Calculation of alpha-cr
CALCULATION SHEET
where:
cr
Fcr
mode
FEd
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
is the factor by which the design loading would have to be
increased to cause elastic instability in a global mode
is the elastic critical buckling load for global instability
based on initial elastic stiffnesses
is the design loading on the structure
Alternative calculation of cr
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Beam-and-column type plane frames in buildings may be checked for sway
mode failure with first order analysis if the criterion cr 10 (resp. cr 15) is
satisfied for each storey. In these structures cr may be calculated using the
following approximate formula, provided that the axial compression in the
beams or rafters is not significant:
H
cr = Ed
V Ed
where: H Ed
H,Ed
is the design value of the horizontal reaction at the bottom
of the storey to the horizontal loads and fictitious horizontal
loads
V Ed
is the total design vertical load on the structure on the
of the storey
H,Ed
is the horizontal displacement at the top of the storey,
to the bottom of the storey, when the frame is loaded
horizontal loads (e.g. wind) and fictitious horizontal
which are applied at each floor level
bottom
relative
with
loads
is the storey height
H,Ed
VEd
h
HEd
EN 1993-1-1
5.2.1 (4)B
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
EN 1993-1-1
5.2.1 (3)
a) Rigid column bases
Calculation of cr
The computer calculation for the relevant load case leads to
38,9
Fcr
= 27, 06 > 10
FEd
1,44
3,50
cr =
38,9
3,50
1,44
second order effects may be
neglected
6,00
6,00
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Alternative calculation of cr
Deformed structure
1
1 = 0,69 mm
h = 3,50m
2 = 0,31 mm
cr,1 =
1, 44
3500
= 28, 41 > 10
466,8 0, 69 0,31
cr ,2 =
1, 44 2 3500
= 34,83 > 10
466,8 2 0,31
second order effects may be neglected
VEd = 466,8 kN
HEd = 1,44 kN
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
EN 1993-1-1
5.2.1 (3)
b) pinned column bases
Calculation of cr
The computer calculation for the relevant load case leads to
Fcr
= 6, 79 < 10
FEd
38,9
1,44
3,50
cr =
38,9
1,44
3,50
second order effects have to be
taken into account
6,00
6,00
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Alternative calculation of cr
EN 1993-1-1
5.2.1 (4)B
Deformed structure
1
1 = 1,79 mm
h = 3,50 m
2 = 1,34 mm
VEd = 466,8 kN
HEd = 1,44 kN
cr,1 =
1, 44
3500
= 23,99 > 10
466,8 1, 79 1,34
cr,2 =
1, 44 2 3500
= 8, 06 < 10
466,8 2 1,34
second order effects have to be taken into account
Example: Calculation of alpha-cr
CALCULATION SHEET
Document Ref:
SX006a-EN-EU
Title
Example: Calculation of alpha-cr
Eurocode Ref
EN 1993-1-1
Made by
Matthias Oppe
Date
June 2005
Checked by
Christian Mller
Date
June 2005
Sheet
of
For multi-storey frames second order sway effects may be calculated by
increasing the horizontal loads HEd (e.g. wind) and equivalent loads VEd
due to imperfections according to first order theory by the factor:
1
1
provided that:
cr
- cr > 3,0
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
- all storeys have a similar distribution of
vertical loads
horizontal loads
frame stiffness with respect to the applied storey shear
forces
here:
cr
1
1
1
6, 79
= 1,172
EN 1993-1-1
5.2.2 (6)B
Example: Calculation of alpha-cr
Example: Calculation of alpha-cr
SX006a-EN-EU.doc
Quality Record
RESOURCE TITLE
Example: Calculation of alpha-cr
Reference(s)
ORIGINAL DOCUMENT
Name
Company
Date
Created by
Matthias Oppe
RWTH
15/06/05
Technical content checked by
Christian Mller
RWTH
15/06/05
1. UK
G W Owens
SCI
7/7/05
2. France
A Bureau
CTICM
17/8/05
3. Sweden
A Olsson
SBI
8/8/05
4. Germany
C Muller
RWTH
10/8/05
5. Spain
J Chica
Labein
12/8/05
G W Owens
SCI
21/05/06
Editorial content checked by
Created on Thursday, February 24, 2011
This material is copyright - all rights reserved. Use of this document is subject to the terms and conditions of the Access Steel Licence Agreement
Technical content endorsed by the
following STEEL Partners:
Resource approved by Technical
Coordinator
TRANSLATED DOCUMENT
This Translation made and checked by:
Translated resource approved by:
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5819)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1093)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (845)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- Ron Tiner - Figure Drawing Without A ModelDocument164 pagesRon Tiner - Figure Drawing Without A ModelBreana Melvin97% (65)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Armare Diafragme A4Document11 pagesArmare Diafragme A4Kalauz EdmondNo ratings yet
- Example of Partial Design FMEA On PencilDocument1 pageExample of Partial Design FMEA On PencilGauravBedreNo ratings yet
- Engine WÄRTSILÄ 18V32 Español PDFDocument350 pagesEngine WÄRTSILÄ 18V32 Español PDFticaren100% (4)
- CP1 10310E1 ManualDocument152 pagesCP1 10310E1 ManualJoseManuelHerreraNúñez50% (2)
- The Instruction Manual of Jinchan Ore Dressing AgentDocument4 pagesThe Instruction Manual of Jinchan Ore Dressing AgentMercedes Guillermina Godoy Barbosa100% (3)
- Calculul La Forta Taietoare A Sectiunii ArmateDocument35 pagesCalculul La Forta Taietoare A Sectiunii ArmateKalauz EdmondNo ratings yet
- Maber MB 2000Document1 pageMaber MB 2000Kalauz EdmondNo ratings yet
- Foc Tema 1Document4 pagesFoc Tema 1Kalauz EdmondNo ratings yet
- Best Practice Guidelines For Scaffolding in NZ 2009Document104 pagesBest Practice Guidelines For Scaffolding in NZ 2009Kalauz Edmond100% (1)
- R ..TC,/ Tili'tj :/-I4,,'1 ) IDocument26 pagesR ..TC,/ Tili'tj :/-I4,,'1 ) IKalauz EdmondNo ratings yet
- Incarcarea Utila Greutate Profil Greutate Beton ( (+ ( (Document1 pageIncarcarea Utila Greutate Profil Greutate Beton ( (+ ( (Kalauz EdmondNo ratings yet
- Dimensionare Stalpi CENTRAL Conform p100Document25 pagesDimensionare Stalpi CENTRAL Conform p100Kalauz EdmondNo ratings yet
- Cbiu ArmareDocument23 pagesCbiu ArmareKalauz EdmondNo ratings yet
- Burne Hogarth - Drawing The Human HeadDocument160 pagesBurne Hogarth - Drawing The Human HeadTheo Haban99% (86)
- Grinda Mixta Otel-BetonDocument6 pagesGrinda Mixta Otel-BetonKalauz EdmondNo ratings yet
- Example Determination of Loads On A Building Envelope PDFDocument8 pagesExample Determination of Loads On A Building Envelope PDFHerdean RemusNo ratings yet
- CT Ch6 Part1Document58 pagesCT Ch6 Part1Mo'men NabilNo ratings yet
- Winch AnalysisDocument21 pagesWinch Analysisvarshasdm19870% (1)
- Mil-B-8976 (Asg) : I 6 February 1969Document12 pagesMil-B-8976 (Asg) : I 6 February 1969kkpatel87No ratings yet
- 9406ph PDocument52 pages9406ph PRana HazemNo ratings yet
- Falling Film Transition and Heat Transfer On Horizontal Circular CylindersDocument4 pagesFalling Film Transition and Heat Transfer On Horizontal Circular CylindersAvijit KarmakarNo ratings yet
- Sets and Venn Diagrams Igcse Questions PDFDocument8 pagesSets and Venn Diagrams Igcse Questions PDFWeteachNo ratings yet
- Excavator Hydraulic System FaultDocument5 pagesExcavator Hydraulic System FaultJoseph JoseNo ratings yet
- Unit 3 Fourier Transforms Questions and Answers - Sanfoundry PDFDocument3 pagesUnit 3 Fourier Transforms Questions and Answers - Sanfoundry PDFzohaibNo ratings yet
- Modification of Impedence MatrixDocument14 pagesModification of Impedence MatrixAarizMalikNo ratings yet
- FCPS-6th-Grade-Science B v218 w4l s1 PDFDocument343 pagesFCPS-6th-Grade-Science B v218 w4l s1 PDFfermeskop80% (5)
- "Intersection Man" - First Four Chapters of A Science Fiction Thriller.Document87 pages"Intersection Man" - First Four Chapters of A Science Fiction Thriller.Hari KumarNo ratings yet
- Burkert Product Overview SensorsDocument54 pagesBurkert Product Overview Sensorssyahrial ramadhanNo ratings yet
- Chapter 6 Rev1 Multiple ReactionDocument37 pagesChapter 6 Rev1 Multiple ReactionHakashiMirudoNo ratings yet
- 25mm MotorsDocument1 page25mm Motorsgreat urduNo ratings yet
- Pierce BCA KitDocument7 pagesPierce BCA KitFei GuanNo ratings yet
- Lecture 17: General Quantum Errors CSS Codes: CPSC 519/619: Quantum Computation John Watrous, University of CalgaryDocument7 pagesLecture 17: General Quantum Errors CSS Codes: CPSC 519/619: Quantum Computation John Watrous, University of CalgaryarcchemNo ratings yet
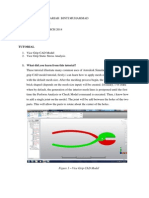
- Tutorial: Figure 1 - Vice Grip CAD ModelDocument5 pagesTutorial: Figure 1 - Vice Grip CAD Modeltotentanz_einhornNo ratings yet
- Arif CV.Document3 pagesArif CV.sheikmoinNo ratings yet
- Volume Five of FiveDocument726 pagesVolume Five of FiveAnonymous 7aTX1mjAsZNo ratings yet
- Biotribology SeminarDocument25 pagesBiotribology Seminarsatyambhuyan_5338070No ratings yet
- RefrenceDocument80 pagesRefrencehamed_physicNo ratings yet
- Variance - Wikipedia, The Free EncyclopediaDocument18 pagesVariance - Wikipedia, The Free EncyclopediaShrabaniPaulNo ratings yet
- Sag and Tension Calculations For Overhead Transmission Lines at High Temperatures - Modified Ruling Span MethodDocument7 pagesSag and Tension Calculations For Overhead Transmission Lines at High Temperatures - Modified Ruling Span MethodKy TaNo ratings yet
- Girgis2007 PDFDocument9 pagesGirgis2007 PDFHimanshu shravgiNo ratings yet
- Surveying ReviewerDocument4 pagesSurveying ReviewerExequiel VecidoNo ratings yet
- Single Cell Culture: 5 Methods (With Diagram) - Plant Tissue CultureDocument6 pagesSingle Cell Culture: 5 Methods (With Diagram) - Plant Tissue Cultureshilpa udamaleNo ratings yet