Professional Documents
Culture Documents
Eulerian Flow Modeling
Uploaded by
Ankit GohelOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Eulerian Flow Modeling
Uploaded by
Ankit GohelCopyright:
Available Formats
1
Lecture 18 - Eulerian Flow Modeling
Applied Computational Fluid Dynamics
Instructor: Andr Bakker
http://www.bakker.org
Andr Bakker (2002-2006)
Fluent Inc. (2002)
2
Contents
Overview of Eulerian-Eulerian multiphase model.
Spatial averaging.
Conservation equations and constitutive laws.
Interphase forces.
Heat and mass transfer.
Discretization.
Solver basics.
3
Eulerian-Eulerian multiphase - overview
Used to model droplets or bubbles of secondary phase(s)
dispersed in continuous fluid phase (primary phase).
Allows for mixing and separation of phases.
Solves momentum, enthalpy, and continuity equations for each
phase and tracks volume fractions.
Uses a single pressure field for all phases.
Uses interphase drag coefficient.
Allows for virtual mass effect and lift forces.
Multiple species and homogeneous reactions in each phase.
Allows for heat and mass transfer between phases.
Can solve turbulence equations for each phase.
4
Methodology
A general multiphase system consists of interacting phases
dispersed randomly in space and time. Interpenetrating continua.
Methods:
Use of continuum theory and thermodynamical principles to
formulate the constitutive equations (ASMM).
Use of microstructural model in which macroscopic behavior is
inferred from particle interaction: Eulerian-Granular.
Use of averaging techniques and closure assumptions to model the
unknown quantities:
Space averaging with no time averaging.
Time averaging with no space averaging.
Ensemble averaging with no space averaging.
space/time or ensemble/space averaging: Eulerian-Eulerian.
5
Two-fluid model (interpenetrating continua)
Deductive approach:
Assume equations for each pure phase.
Average (homogenize) these equations.
Model the closure terms.
Inductive approach:
Assume equations for interacting phases.
Model the closure terms.
6
Application of the general transport theorem to a property
k
gives the general balance law and its jump condition:
Continuity equation:
Momentum equation:
0 , 0 , = = =
k k k k
J
&
r
k k k k k k k k k
F I P J u
r
&
r
= = = , ,
k k k k
k
J u
t
&
r
r
= + +
0 ) ) ( (
, 1
= +
=
k ki ki i k
n
i k i
k
J n n u u
r
r r
Spatial averaging: basic equations
7
Consider an elementary control volume d bounded by the
surface dS.
Length scales:
Volumes:
Averaging volume and coordinate system:
t k
l d l L ~ >> >>
=
=
n
i
i
t d d
1
) (
2
x
1
x
3
x
p
x
r
i
k
ki
n
r
d
k
d
n
r
1
y
2
y
3
y
Spatial averaging
8
Definitions:
Volume average Intrinsic phasic average.
Volume phase fraction:
>= <
i
d
d t y x f
d
f
'
) , (
1 r r
= > <
k
d
k
k
d t y x f
d
f
'
) , (
1 r r
=
d
t x d
p k
k
) , (
r
1
1
=
=
n
k
k
k k
f f > < >= <
Space averaging: basic equations
9
For all k-volumes that are differentiables, (Gray and Lee (1977),
Howes and Whitaker (1985)).
Temporal derivative:
Spatial derivative:
Next, apply averaging to the conservation equations.
S d n u f
d
f
t t
f
ki
dS
ki
ki
'
1 r r
> <
>=
<
S d n f
d
f f
ki
dS
ki
'
1
+ > < >= <
v
> <
>
< f
t t
f
> < > < f f
Space averaging: averaging theorems
10
k k k k k k k k k k k k k k k k k k k
F P u u u
t
> < + > < + > < = > < + > <
r r r
{ } S d n P u u u
d
ki
dS
k k k ki k k
ki
'
) (
1 r r r r
+
= > < + > <
ki
dS
k ki k k k k k k k k k
S d n u u
d
u
t
'
) (
1 r r r r
Space averaging: conservation equations
Continuity equation:
Momentum equation:
mass transfer term
interaction term
11
Drag is caused by relative motion between phases.
Commonly used drag models (fluid-fluid multiphase).
Schuh et al. (1989).
Schiller and Naumann (1935).
Morsi and Alexander (1972).
Schwarz and Turner (1988; for bubble columns).
Symmetric law.
Many researchers devise and implement their own drag models
for their specific systems.
, 0 ) (
1
=
=
n
i
k i ik
u u K
r r
ik
drag
k k ik
f
K
=
i
k
k
ik
d
18
2
=
Interphase forces
12
Interphase forces: drag force models
Fluid-fluid drag functions
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
10 100 1000 10000 100000
Re
Cd
Schiller and
Naumann
Schuh et al.
Morsi et Alexander
( )
>
+
=
1000 Re 44 . 0
1000 Re Re 15 . 0 1 24
687 . 0
D
C
(Re) are , , where
Re Re
3 2 1
2
3 2
1
f a a a
a a
a C
D
+ + =
Schiller and Naumann
Schuh et al.
Morsi and Alexander
( )
( )
>
> +
< +
=
2500 Re 4008 . 0
2500 Re 200 Re / Re 0135 . 0 Re 914 . 0 24
200 Re 0 Re 15 . 0 1 24
282 . 0
687 . 0
D
C
13
Virtual mass effect: caused by relative acceleration between
phases Drew and Lahey (1990).
Virtual mass effect is significant when the second phase density is
much smaller than the primary phase density (i.e., bubble column).
Lift force: caused by the shearing effect of the fluid onto the
particle Drew and Lahey (1990).
Lift force usually insignificant compared to drag force except when
the phases separate quickly and near boundaries.
|
\
|
+
= ) ( ) (
, s s
s
f f
f
f s vm fs vm
u u
t
u
u u
t
u
C K
r r
r
r r
r
) ( ) (
, f s f f s L fs k
u u u C K
r r r
=
Interphase forces: virtual mass and lift
14
Modeling heat transfer
Conservation equation of phase enthalpy.
k k k k k
k
k k k k k k k k
R u S P u
t
P
h u h
t
+ + +
= +
r r r
: ) ( ) ( ) (
) ( ) (
1
ik k ki k i
n
k
ki k
h h m T T q + +
=
&
r
Viscous dissipation
term
Originates from
work term for
volume fraction
changes
Energy sources
e.g., radiation
15
k k k k k
k
k k k k k k k k
R u S P u
t
P
h u h
t
+ + +
= +
r r r
: ) ( ) ( ) (
) ( ) (
1
ik k ki k i
n
k
ki k
h h m T T q + +
=
&
r
Interphase heat
transfer term
Heat conduction
Energy transfer with
mass transfer
Modeling heat transfer
Conservation equation of phase enthalpy.
16
Assume Fouriers law:
For granular flows
k
is obtained from packed bed conductivity
expression, Kuipers, Prins and Swaaij (1992).
Near wall heat transfer is calculated as in single phase.
All standard boundary conditions for temperature can be
implemented for multiphase.
k k k
T q =
r
Heat conduction
17
The interphase heat transfer coefficient is given by.
Granular Model (Gunn, 1978).
Fluid-fluid model.
2
6
i
i i k
ik
d
Nu
=
) Pr Re 7 . 0 1 )( 5 10 7 (
3
1
2 . 0 2
+ + =
f f s
Nu
3
1
7 . 0 2
Pr Re ) 2 . 1 4 . 2 33 . 1 (
f f
+ +
3 . 0 5 . 0
Pr Re 6 . 0 2 + =
i
Nu
k
i k i k k
d u u
= Re
k
k k p
C
,
Pr =
Interphase heat transfer
18
Conservation equation for the mass fraction of the species i
in the phase k:
Here is the diffusivity of the species in the mixture of the
respective phase, is the rate of production/destruction of the
species.
Thermodynamic relations an state equations for the phase k are
needed.
When calculating mass transfer the shadow technique from
Spalding is used to update diameter of the dispersed phase.
i
k
i
k
i
k k k
i
k k k k
i
k k k
m m D m u m
t
&
r
+ = +
) ( ) ( ) (
i
k
m
i
k
D
i
k
m&
Conservation of species
19
Evaporation and condensation:
For liquid temperatures saturation temperature, evaporation rate:
For vapor temperatures saturation temperature, condensation rate:
User specifies saturation temperature and, if desired, time relaxation
parameters r
l
and r
v
(Wen Ho Lee (1979)).
Unidirectional mass transfer, r is constant:
( )
sat
sat l l l v
v
T
T T r
m
=
&
( )
sat
v sat v v l
l
T
T T r
m
=
&
1 2 12
r m = &
Modeling mass transfer
20
Coupled solver algorithms (more coupling between phases).
Faster turn around and more stable numerics.
High order discretization schemes for all phases.
More accurate results.
Implicit/Full Elimination
Algorithm v4.5
TDMA Coupled
Algorithm v4.5
Multiphase Flow Solution
Algorithms
Only Eulerian/Eulerian
model
Solution algorithms for multiphase flows
21
Momentum equation for primary and secondary phase:
Elimination of secondary phase gives primary phase:
Secondary phase has similar form.
Applicable to N phases.
( )
s p p p nb p nb p eff p
s s nb s nb
s
p p nb p nb p s
s
p
b b u a u a
b u a
k a
k
b u a u a
k a
k
a
, , , ,
, , , ,
+ + =
+
+
+ + =
|
|
\
|
+
+
( )
( )
s s nb s nb s s p
p p nb p nb s p p
b u a u k a u k
b u a u k u k a
+ = + +
+ = +
, ,
, ,
Full elimination algorithm
22
Discretized equations of primary and secondary phase are in
matrix form:
Results in a tri-diagonal matrix consisting of submatrices
Closer coupling in each iteration gives faster convergence
B U U
b
b
u
u
a
a
u
u
k a k
k k a
nb nb
s
p
s nb
p nb
s nb
p nb
s
p
s
p
r r r
+ =
|
|
\
|
+
|
|
\
|
|
|
\
|
=
|
|
\
|
|
|
\
|
+
+
A A
,
,
,
,
0
0
|
|
|
|
|
\
|
=
|
|
|
|
|
\
|
|
|
|
|
|
\
|
n n
nn
C
C
C
C
U
U
U
U
A
A A
A A A
A A
r
r
r
r
r
r
r
r
3
2
1
3
2
1
33 32
23 22 21
12 11
0 0 0
0 0
0
0 0
Coupled TDMA-algorithm
23
Solution algorithm for multiphase
Typical algorithm:
Get initial and boundary conditions.
Perform time-step iteration.
Calculate primary and secondary phase velocities.
Calculate pressure correction and correct phase velocities, pressure
and phase fluxes. Pressure is shared by all phases.
Calculate volume fraction.
Calculate other scalars. If not converged go to step three.
Advance time step and go to step two.
24
Solution guidelines
All multiphase calculations:
Start with a single-phase calculation to establish broad flow patterns.
Eulerian multiphase calculations:
Copy primary phase velocities to secondary phases.
Patch secondary volume fraction(s) as an initial condition.
Set normalizing density equal to physical density.
Compute a transient solution.
Use multigrid for pressure.
25
Summary
Eulerian-Eulerian is the most general multiphase flow model.
Separate flow field for each phase.
Applicable to all particle relaxation time scales.
Includes heat/mass exchange between phases.
Available in both structured and unstructured formulations.
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (894)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- How to trade forex like the banksDocument34 pagesHow to trade forex like the banksGeraldo Borrero80% (10)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- CpE194 Lab Experiment # 1 - MTS-88 FamiliarizationDocument4 pagesCpE194 Lab Experiment # 1 - MTS-88 FamiliarizationLouieMurioNo ratings yet
- Group 7 Scope StatementDocument17 pagesGroup 7 Scope Statementapi-335995226100% (4)
- Develop Your Kuji In Ability in Body and MindDocument7 pagesDevelop Your Kuji In Ability in Body and MindLenjivac100% (3)
- 8 DaysDocument337 pages8 Daysprakab100% (1)
- Decision MatrixDocument12 pagesDecision Matrixrdos14No ratings yet
- Mcad BookDocument2 pagesMcad BookAnkit GohelNo ratings yet
- Teaching Numerical Analysis with MathcadDocument17 pagesTeaching Numerical Analysis with Mathcadsori1386No ratings yet
- ANU Scilab Tutorials IntroductionDocument93 pagesANU Scilab Tutorials Introductionphanindra_prasad_1No ratings yet
- Tutorial MathcadDocument13 pagesTutorial MathcadFabrizziobiNo ratings yet
- Excel 2 MathcadDocument3 pagesExcel 2 MathcadAnkit GohelNo ratings yet
- How To Iteration On ExcelDocument8 pagesHow To Iteration On ExcelUnique O'shopNo ratings yet
- Refrigeration and Air ConditioningDocument21 pagesRefrigeration and Air ConditioningShiva Kumar H MNo ratings yet
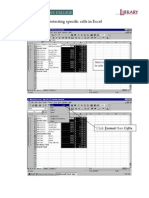
- Protecting Specific Cells in Excel: Select Cells That You Wish To Be Able To Be Changed/editedDocument3 pagesProtecting Specific Cells in Excel: Select Cells That You Wish To Be Able To Be Changed/editedAnkit GohelNo ratings yet
- How To Iteration On ExcelDocument8 pagesHow To Iteration On ExcelUnique O'shopNo ratings yet
- How To Iteration On ExcelDocument8 pagesHow To Iteration On ExcelUnique O'shopNo ratings yet
- Computer HIstoryDocument95 pagesComputer HIstoryAnkit GohelNo ratings yet
- 9451 181906Document2 pages9451 181906Ankit GohelNo ratings yet
- Turbulent Flow and TransportDocument2 pagesTurbulent Flow and TransportAnkit GohelNo ratings yet
- Configuring Nagios On Client For OSSIMDocument10 pagesConfiguring Nagios On Client For OSSIMMaixender NganareNo ratings yet
- Risk Assessment For Modification of Phase 1 Existing Building GPR TankDocument15 pagesRisk Assessment For Modification of Phase 1 Existing Building GPR TankAnandu Ashokan100% (1)
- Literary Text Analysis WorksheetDocument1 pageLiterary Text Analysis Worksheetapi-403444340No ratings yet
- Balkan TribesDocument3 pagesBalkan TribesCANELO_PIANONo ratings yet
- Materi Green SCMDocument38 pagesMateri Green SCManandaailanthusNo ratings yet
- DELA PENA - Transcultural Nursing Title ProposalDocument20 pagesDELA PENA - Transcultural Nursing Title Proposalrnrmmanphd0% (1)
- A. Johnston - Naturalism and Anti NaturalismDocument47 pagesA. Johnston - Naturalism and Anti NaturalismaguiaradNo ratings yet
- ME927 Energy Resources and Policy SyllabusDocument5 pagesME927 Energy Resources and Policy SyllabusAditya Whisnu HeryudhantoNo ratings yet
- DCinv V6 Rev2 CleanDocument38 pagesDCinv V6 Rev2 Cleanyasirarafat91No ratings yet
- Tabelas Normativas DinDocument2 pagesTabelas Normativas DinDeimos PhobosNo ratings yet
- Time Series Data Analysis For Forecasting - A Literature ReviewDocument5 pagesTime Series Data Analysis For Forecasting - A Literature ReviewIJMERNo ratings yet
- Páginas Desdeingles - Sep2008Document1 pagePáginas Desdeingles - Sep2008anayourteacher100% (1)
- Lasers OpDocument6 pagesLasers OpAndrian PrimadyaNo ratings yet
- RealPOS 70Document182 pagesRealPOS 70TextbookNo ratings yet
- Topic 4 Petrophysics - Part 4Document32 pagesTopic 4 Petrophysics - Part 4Aneesch PreethaNo ratings yet
- DEMO 2 Critical Reading As ReasoningDocument3 pagesDEMO 2 Critical Reading As ReasoningConnieRoseRamosNo ratings yet
- Roman Questions II PDFDocument738 pagesRoman Questions II PDFjlinderski100% (3)
- Omega Fluid PDFDocument2 pagesOmega Fluid PDFapatzinfedNo ratings yet
- Two Monuments by C Mann 1493 Copy - PDF - OcredDocument23 pagesTwo Monuments by C Mann 1493 Copy - PDF - OcredStephania FrancoNo ratings yet
- D5435 PDFDocument6 pagesD5435 PDFZamir Danilo Morera ForeroNo ratings yet
- 1 PDFDocument14 pages1 PDFPM JFNo ratings yet
- ASTM C 136 Sieve Analysis of Fine and Coarse Aggregates (D)Document5 pagesASTM C 136 Sieve Analysis of Fine and Coarse Aggregates (D)Yasir DharejoNo ratings yet
- Shailesh Sharma HoroscopeDocument46 pagesShailesh Sharma Horoscopeapi-3818255No ratings yet
- Carnot CycleDocument3 pagesCarnot CyclealexontingNo ratings yet