Professional Documents
Culture Documents
967 - 6% Magnetic-Field-Induced Strain by Twin-Boundary Motion in Ferromagnetic Ni-Mn-Ga PDF
967 - 6% Magnetic-Field-Induced Strain by Twin-Boundary Motion in Ferromagnetic Ni-Mn-Ga PDF
Uploaded by
mohammadreza91Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
967 - 6% Magnetic-Field-Induced Strain by Twin-Boundary Motion in Ferromagnetic Ni-Mn-Ga PDF
967 - 6% Magnetic-Field-Induced Strain by Twin-Boundary Motion in Ferromagnetic Ni-Mn-Ga PDF
Uploaded by
mohammadreza91Copyright:
Available Formats
Iowa State University
Digital Repository @ Iowa State University
Ames Laboratory Publications and Papers
Ames Laboratory
8-7-2000
6% magnetic-field-induced strain by twinboundary motion in ferromagnetic NiMnGa
S. J. Murray
Massachusetts Institute of Technology
M. Marioni
Massachusetts Institute of Technology
S. M. Allen
Massachusetts Institute of Technology
R. C. O'Handley
Massachusetts Institute of Technology
Thomas A. Lograsso
Iowa State University, lograsso@ameslab.gov
Follow this and additional works at: http://lib.dr.iastate.edu/ameslab_pubs
Part of the Condensed Matter Physics Commons, and the Metallurgy Commons
The complete bibliographic information for this item can be found at http://lib.dr.iastate.edu/
ameslab_pubs/125. For information on how to cite this item, please visit http://lib.dr.iastate.edu/
howtocite.html.
This Article is brought to you for free and open access by the Ames Laboratory at Digital Repository @ Iowa State University. It has been accepted for
inclusion in Ames Laboratory Publications and Papers by an authorized administrator of Digital Repository @ Iowa State University. For more
information, please contact hinefuku@iastate.edu.
APPLIED PHYSICS LETTERS
VOLUME 77, NUMBER 6
7 AUGUST 2000
6% magnetic-field-induced strain by twin-boundary motion
in ferromagnetic NiMnGa
S. J. Murray,a) M. Marioni, S. M. Allen, and R. C. OHandleyb)
Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
T. A. Lograsso
Ames Laboratory, United States Department of Energy, Iowa State University, Ames, Iowa 50014
Received 18 April 2000; accepted for publication 9 June 2000
Field-induced strains of 6% are reported in ferromagnetic NiMnGa martensites at room
temperature. The strains are the result of twin boundary motion driven largely by the Zeeman energy
difference across the twin boundary. The strain measured parallel to the applied magnetic field is
negative in the sample/field geometry used here. The strain saturates in fields of order 400 kA/m and
is blocked by a compressive stress of order 2 MPa applied orthogonal to the magnetic field. The
strain versus field curves exhibit appreciable hysteresis associated with the motion of the twin
boundaries. A simple model accounts quantitatively for the dependence of strain on magnetic field
and external stress using as input parameters only measured quantities. 2000 American Institute
of Physics. S0003-69510000832-9
Ferromagnetic shape memory alloys FSMAs moved
from a hypothetical new class of active materials, to join
piezoelectric and magnetostrictive materials, upon observation of a 0.2% magnetic-field-induced strain in a single crystal of Ni2MnGa in 1996.1 By way of comparison, piezoelectric materials2 show strains of order 0.1%2 and the leading
magnetostrictive material, Terfenol-D,3 shows a fieldinduced strain of about 0.24%. This 0.2% strain represents
only a small fraction of the 6% or 7% transformation strain
expected to be accessible by field-induced twin selection in
NiMnGa FSMAs. Extensional strains of 0.5% have been
observed in martensitic Fe70Pd30 crystals4 at 17 C and
2.3% in Ni2MnGa martensitic crystals5 at 8 C. Shear
strains of 5.7% have been reported at room temperature in
NiMnGa martensites.6
Here we report measurements of field-induced generation of the full extensional strain associated with the crystallographic distortion in a ferromagnetic shape memory alloy.
An initial single-variant state is achieved by application of a
compressive stress of order 1 MPa to a sample of an offstoichiometry crystal of NiMnGa. The strain is produced
by application of a field of typically 400 kA/m 5 kOe orthogonal to the compressive stress direction. High-speed
photographs reveal the nearly complete transformation of the
sample from one twin variant to another by twin boundary
motion during application of the field. The form of the strain
as a function of applied field and stress is quantitatively well
described by a thermodynamic model7,8 that includes Zeeman energy, magnetocrystalline anisotropy, external stress,
and an internal restoring force. The observed hysteresis is
due to the threshold stress needed to initiate twin boundary
motion and can be determined independently from a stress
strain curve. There are no adjustable parameters in the
model.
The composition weighed out for growth,
Ni47.4Mn32.1Ga20.5, was chosen slightly off the Heusler stoichiometry, Ni2MnGa. This was done in order to render alloys having Curie temperatures greater than the martensite
transformation temperature, which in turn was to be greater
than room temperature.9 Crystals were grown by the Bridgman technique at Ames Laboratory. High purity nickel, manganese, and gallium were arc melted into buttons and then
drop cast into a chilled copper mold. The as-cast ingots were
placed in alumina crucibles and were heated to 1350 C for 1
h to allow homogenization before withdrawing the sample
from the heat zone at a rate of 5.0 mm/h. In order to minimize evaporation of the Mn during crystal growth, the furnace was backfilled to a positive pressure of 6.8105 Pa
with purified argon after the chamber and sample had been
outgassed at 1350 C under vacuum. The single crystal boule
measured 1 cm in diameter and 5 cm in length. Electron
probe microanalysis showed the composition to vary along
the boule axis with Mn content increasing and Ga content
decreasing in the growth direction.
After Laue orientation, several samples were cut from
the crystal boule by electric discharge milling. Rectangular
prismatic samples measuring about 6 mm by 6 mm by 20
mm, were cut to have their faces parallel to the faces of the
m unit cell.8 The sample
high-temperature, L2 1 Fm3
described here has an analyzed composition of
Ni49.8Mn28.5Ga21.7, with a Curie temperature of 95 C. Upon
transformation to the tetragonally distorted (I4/mmm) martensitic phase below 45 C, twinning can occur along 112
planes 101 or 011 in Fm3m. A separate disk-shaped
sample measuring 3 mm diameter by 1 mm thick was made
of essentially the same composition as the prism. This disk
sample has a 100 direction in its plane and was prepared
for magnetic anisotropy measurements. The single-variant
state was established in the disk by application of a magnetic
field while the sample was cured in epoxy. A twin-free state
can be achieved either by application of a stress of order 1
MPa or a magnetic field of order 400 kA/m. After curing of
Present address: Mide Corporation, 56 Rogers St., Cambridge, MA.
Electronic mail: bobohand@mit.edu
0003-6951/2000/77(6)/886/3/$17.00
886
2000 American Institute of Physics
Downloaded 05 Jan 2001 to 147.155.1.95. Redistribution subject to AIP copyright, see http://ojps.aip.org/aplo/aplcpyrts.html.
Murray et al.
Appl. Phys. Lett., Vol. 77, No. 6, 7 August 2000
887
FIG. 1. Field dependence of magnetization at room temperature in singlevariant, martensitic NiMnGa crystal with field applied parallel and perpendicular to 001Ref. 11.
the epoxy, the single-variant state was retained. Room temperature magnetization curves taken parallel and perpendicular to the c axis and in the plane of the disk are shown in Fig.
1. They indicate the strength of the uniaxial magnetic anisotropy to be K u1 1.5105 J/m3. The saturation magnetization
at room temperature is 0 M s 0.62 T. Tickle and James10
measured the anisotropy Ni51.3Mn24.0Ga24.7 single crystals
constrained to be in the single-variant state. They reported
K u 2.45105 J/m3 at 17 C.
For the field-induced strain measurements, the prismatic
sample was placed with its short dimension along the field
axis of an electromagnet while its long dimension vertical
supported a nonmagnetic push rod extending above the electromagnet and ending in a platform. Dead weights were
placed on the platform to apply a stress to the sample. The
displacement of the platform referenced to the sample base
was measured with an eddy current proximity sensor. A
stress of 1.0 MPa was found to render the sample in a nearly
single-variant state.
Figure 2 shows the results of field-induced strain measurements in a Ni49.8Mn28.5Ga21.7 single crystal at room temperature for various axial external stresses that oppose the
field-induced strain. The sketch shows the orientation of the
magnetization, magnetic field, and external stress relative to
the twinned sample. The magnetization vectors are shown
parallel to the tetragonal c axis in each variant. The photographs are frames from a high-speed 1000 frames/s video
taken on the sample in the initially stressed state approximately 0.34 MPa at H2105 A/m a, at two intermediate
states of actuation b, c, and at saturation after about 23 ms
d. The images show that upon application of a transverse
field, twins magnetized parallel to the field darker contrast
appear and grow, causing the sample to extend vertically
against the applied stress. The graph shows that the strain
increases sharply beyond about 200 kA/m and saturates at
about 400 kA/m. Upon removal of the field, the sample remains in an essentially transversely magnetized vertically
extended state for 0.5 MPa. Repeating the field cycle
under incrementally greater stress results in an increase in
the threshold field at which most strain occurs. At stress
FIG. 2. Top: Orientation of M, H, and relative to the twinned sample.
Selected high-speed video frames show the sample in the initially compressed ( 0.2 MPa) state (H0), in two intermediate states, and in the
magnetically saturated, fully strained state, respectively. Bottom: Fieldinduced strain at various external opposing stresses at room temperature for
a Ni49.8Mn28.5Ga21.7 single crystal.
levels in excess of 1.1 MPa, the initial stress-stabilized state
is reestablished upon removal of the field. At still higher
stresses, the e H curves are sheared over and the full transformation strain is no longer achieved. A stress of 2 MPa 44
lb/cm2 reduces the maximum field-induced strain to 0.6%.
The hysteresis appears nonmonotonic in applied stress. Essentially the full transformation strain is achieved in this case
for stresses less than 1.0 MPa. Other samples from the same
boule have shown strains of 5.7% at saturation.
Phenomenological models describing the field-induced
motion of twin boundaries in FSMAs generally include the
Zeeman energy, magnetic anisotropy energy, an internal restorative elastic energy, and an external stress.7,8,12 The fielddependent strain may be expressed as a function of the volume fraction, f i , of each variant: e(H)e 0 f (H), where e 0
is the transformation strain and f f 1 1/2. The equivariant
state, f 1 f 2 1/2, is defined as e 0 0.7 Micromagnetic
models5,10,13 may also include a magnetostatic energy that
tends to restore M to zero when the field vanishes. The action
of the external stress depends on its orientation relative to the
field-induced deformation. The stress here is oriented to oppose the field-induced strain. The results of the model are
summarized by
e H e 0 f
2K u h 1h/2 e 0
,
C effe 0
where hM s H/2K u and C eff is the effective modulus of the
twinned state that accounts for the elastic energy stored in
parts of the material that do not respond to the field by twinboundary motion.7,12 The data of Fig. 2 are described with
this model using the measured NiMnGa parameters:
0 M s 0.6 T, K u1 1.8105 J/m3, 0 0.06, and C eff2
Downloaded 05 Jan 2001 to 147.155.1.95. Redistribution subject to AIP copyright, see http://ojps.aip.org/aplo/aplcpyrts.html.
888
Murray et al.
Appl. Phys. Lett., Vol. 77, No. 6, 7 August 2000
FIG. 3. Left, calculated strain vs applied field curves from Eq. 1 and right,
calculated strain vs stress with overlaid experimental data.
107 N/m2. The model results displayed in Figs. 3a and
3b show that these parameters give a reasonable reproduction of the major trends in the experimental data, namely the
shape of e(H), as well as the increase in threshold field and
decrease in field-induced strain with increasing external
stress. The model does not account for the observed change
in coercivity with external stress. The predicted decrease in
saturation strain with increasing stress Fig. 3b also gives a
reasonable fit to the data.
The coercivity is introduced into the model in an ad hoc
manner external field is expressed as HH c for decreasing
or increasing field strength, respectively but its value is derived from the mechanical stress strain curves of the crystal
Fig. 4. The mechanical properties of FSMAs in the martensitic phase are similar to those of conventional SMAs. With
increasing stress, the material first shows a modulus, C 0 ,
characteristic of the single-variant state. Above a critical
FIG. 4. Stressstrain behavior of martensitic Ni-Mn-Ga alloys.
stress, 0 , at which deformation by twin boundary motion
initiates, the modulus decreases to C tb and the material may
strain to its full transformation strain, e 0 , after which it is
mechanically detwinned. For larger stresses, the modulus reverts to its single-variant value. Values of the parameters in
Fig. 4 measured for Ni2MnGa crystals are typically of
order11,14 0 1 MPa, C 0 2 GPa, e 0 0.06, and C tb
18 MPa. The coercivity is given by H c e 0 / 0 M s
100 kA/m.
In summary, strains of 6% have been produced at room
temperature in single crystals of NiMnGa by application
of fields of order 400 kA/m under an opposing stress of order
1 MPa. The strain is the result of field-induced twin boundary motion. The form of the dependence of the strain on field
and stress is well described by a phenomenological model
with no adjustable parameters; all parameters are independently measured.
The authors appreciate the support of this work by grants
from ONR N00014-99-1-0506 DARPA N00014-99-10684, a subcontract from Boeing corporation on a DARPA
grant, and the Finnish Academy of Sciences with a consortium of Finnish companies through Helsinki University of
Technology.
1
K. Ullakko, J. K. Huang, C. Kantner, V. V. Kokorin, and R. C.
OHandley, Appl. Phys. Lett. 69, 1966 1996.
2
G. H. Haertling, J. Am. Chem. Soc. 82, 797 1999.
3
J. R. Cullen, A. E. Clark, and K. B. Hathaway, in Handbook of Materials
Science, edited by K. H. J. Buschow VCH, Amsterdam, 1997, Chap. 16.
4
R. D. James and M. Wuttig, Philos. Mag. A 77, 1273 1998.
5
R. Tickle, R. D. James, T. Shield, M. Wuttig, and V. V. Kokorin, IEEE
Trans. Magn. 35, 4301 1999.
6
S. J. Murray, M. Marioni, A. Kukla, J. Robinson, R. C. OHandley, and S.
M. Allen, J. Appl. Phys. 87, 5474 2000.
7
R. C. OHandley, J. Appl. Phys. 83, 3263 1998.
8
R. C. OHandley, S. J. Murray, M. Marioni, H. Nembach, and S. M.
Allen, J. Appl. Phys. 87, 4712 2000.
9
S. J. Murray, M. Farinelli, C. Kantner, J. K. Huang, S. M. Allen, and R. C.
OHandley, J. Appl. Phys. 83, 7297 1998.
10
R. Tickle and R. D. James, J. Magn. Magn. Mater. 195, 627 1999.
11
S. J. Murray, PhD thesis, Massachusetts Institute of Technology, January,
2000.
12
A. A. Likhachev and K. Ullakko, Eur. Phys. J. B 14, 263 2000.
13
R. D. James and D. Kinderlehrer, Philos. Mag. B 68, 237 1993; J. Appl.
Phys. 76, 7012 1994.
14
V. V. Martinov and V. V. Kokorin, J. Phys. III 2, 739 1992; 2, 739
1992.
Downloaded 05 Jan 2001 to 147.155.1.95. Redistribution subject to AIP copyright, see http://ojps.aip.org/aplo/aplcpyrts.html.
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5813)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (844)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- ACCA Manual S 2013 Public Review v1 00Document344 pagesACCA Manual S 2013 Public Review v1 00Pubudu Charaka Kudahetti100% (5)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- BP Flowback ProceduresDocument10 pagesBP Flowback ProceduresAlexander KlmNo ratings yet
- Us 5988287Document14 pagesUs 5988287mohammadreza91No ratings yet
- Viii/Ii/Ii": United States Patent (191 (11) Patent Number: 4,708,208Document9 pagesViii/Ii/Ii": United States Patent (191 (11) Patent Number: 4,708,208mohammadreza91No ratings yet
- References Cited Robiatiorlial Movergents. Pat Least One ElaitigallybexaatrlidDocument7 pagesReferences Cited Robiatiorlial Movergents. Pat Least One Elaitigallybexaatrlidmohammadreza91No ratings yet
- United States Patent: (10) Patent N0.: Hoifman Et Al. (45) Date 0f PatentDocument10 pagesUnited States Patent: (10) Patent N0.: Hoifman Et Al. (45) Date 0f Patentmohammadreza91No ratings yet
- Us5361479 PDFDocument5 pagesUs5361479 PDFmohammadreza91No ratings yet
- Ullltbd States Patent (19) (11) Patent Number: 5,143,154: Mody Et Al. (45) Date of Patent: Sep. 1, 1992Document7 pagesUllltbd States Patent (19) (11) Patent Number: 5,143,154: Mody Et Al. (45) Date of Patent: Sep. 1, 1992mohammadreza91No ratings yet
- United States Patent (19) : Wood (45) Date of Patent: Jan. 8, 1985Document5 pagesUnited States Patent (19) : Wood (45) Date of Patent: Jan. 8, 1985mohammadreza91No ratings yet
- 11111111mumnlllgglotgggglgggggnn - : United States Patent (19) (11) Patent Number: 5,613,555Document5 pages11111111mumnlllgglotgggglgggggnn - : United States Patent (19) (11) Patent Number: 5,613,555mohammadreza91No ratings yet
- United States Patent (191 (11) Patent Number: 5 363 542: Sorem Et A1. (45) Date of Patent: Nov. 15, 1994Document6 pagesUnited States Patent (191 (11) Patent Number: 5 363 542: Sorem Et A1. (45) Date of Patent: Nov. 15, 1994mohammadreza91No ratings yet
- PipesDocument25 pagesPipesSidesway 26No ratings yet
- Design of Water Tanks: by Dr. G.S.Suresh, Professor, Civil Engineering Department, NIE, MysoreDocument24 pagesDesign of Water Tanks: by Dr. G.S.Suresh, Professor, Civil Engineering Department, NIE, MysoreKawan EngNo ratings yet
- Specific HeatDocument12 pagesSpecific Heatlubuguin3230272No ratings yet
- Chapter 1 SolutionsDocument3 pagesChapter 1 SolutionsRicardo SudNo ratings yet
- Chapter 04 - Basics of StaticsDocument16 pagesChapter 04 - Basics of StaticsdeepakNo ratings yet
- Subject: Simulation Process Student: Samuel Lepe de Alba Teacher: Dr. Marcos Alberto Coronado Ortega Topic: Transfer BlocksDocument21 pagesSubject: Simulation Process Student: Samuel Lepe de Alba Teacher: Dr. Marcos Alberto Coronado Ortega Topic: Transfer BlocksSamuel LepeNo ratings yet
- Ong 2018Document22 pagesOng 2018juanNo ratings yet
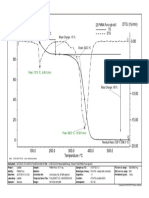
- TG /% DTG / (%/min) : Onset: 130.3 °C Mass Change: - 15 %Document1 pageTG /% DTG / (%/min) : Onset: 130.3 °C Mass Change: - 15 %Danay ManzoNo ratings yet
- FRP Slab Flexure Strengthening With TYFO Fibrwrap System: Retrofitting of Anglo WarehouseDocument5 pagesFRP Slab Flexure Strengthening With TYFO Fibrwrap System: Retrofitting of Anglo Warehouseheherson juanNo ratings yet
- Fillet Welds Loaded in The Connection Plane (Lap Joints)Document6 pagesFillet Welds Loaded in The Connection Plane (Lap Joints)MoonzeNo ratings yet
- Fem VofDocument11 pagesFem VofkhabiranNo ratings yet
- R-134a TableDocument3 pagesR-134a Tablecj100% (1)
- Agitation and Mixing (My Presentation)Document22 pagesAgitation and Mixing (My Presentation)Aleem Choudhry100% (1)
- 3 4 PDFDocument3 pages3 4 PDFMarjoko SantosoNo ratings yet
- TDP-634 Split Systems PDFDocument56 pagesTDP-634 Split Systems PDFjadewest100% (1)
- Effect of Small Circular Opening On The Shear and Flextural Behavior and Ultimate Strength of Reinforced Concrete Beams Using Normal and High Strength ConcreteDocument14 pagesEffect of Small Circular Opening On The Shear and Flextural Behavior and Ultimate Strength of Reinforced Concrete Beams Using Normal and High Strength ConcreteSandeep ShridharNo ratings yet
- Flow Properties of Stirred Yogurt Calculation of The PDFDocument22 pagesFlow Properties of Stirred Yogurt Calculation of The PDFandres332No ratings yet
- Thermal Physics Lecture 11Document8 pagesThermal Physics Lecture 11OmegaUserNo ratings yet
- 4th Grade - Lesson Overview-States of MatterDocument2 pages4th Grade - Lesson Overview-States of MatterlchamblessNo ratings yet
- Course Outline: Meng6302 Advanced Mechanics of SolidsDocument7 pagesCourse Outline: Meng6302 Advanced Mechanics of SolidsKKDhNo ratings yet
- Siamak Shahbazi (2016)Document14 pagesSiamak Shahbazi (2016)kashifNo ratings yet
- BS 7910Document12 pagesBS 7910ggsachary0% (1)
- Fastener AnalysisDocument57 pagesFastener AnalysisAnonymous 3B9kXrNo ratings yet
- (Asce) 0733 9410 (1993) 119:1 PDFDocument17 pages(Asce) 0733 9410 (1993) 119:1 PDFHei Kan ChengNo ratings yet
- BKF 2453 Chemical Reaction EngineeringDocument6 pagesBKF 2453 Chemical Reaction EngineeringThurgah VshinyNo ratings yet
- Airfoil Selection PDFDocument3 pagesAirfoil Selection PDFELMER VILLEGASNo ratings yet
- Nlewis65,+134 136,143 Sandall 5 No 3 SUMMER 1971 CEEDocument4 pagesNlewis65,+134 136,143 Sandall 5 No 3 SUMMER 1971 CEEWellie TwinzaloNo ratings yet
- Fluid IIDocument2 pagesFluid IIJefara 01No ratings yet