22 NEURAL DYNAMICS MODEL FOR ENGINEERING DESIGN OPTIMIZATION

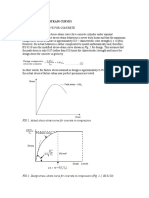
Figure 3.2 Effective widths of cold-formed steel beams in bending: (a) Shapes with stiffened compression flange;
(b) Shapes with unstiffened compression flange

3.3.1
Bending Strength Constraint
The maximum design bending moment, Mmax, must be less than or equal to the design bending strength,
Md.

(3.5)

For beams with full lateral support, Md is the minimum value obtained from considerations of initiation of
yielding or inelastic reserve capacity and the shear lag effects. If the beam does not have full lateral support
Eq. (3.5) has to be satisfied in each unbraced segment where Mmax is the maximum design bending moment
in the segment under consideration and Md is the design lateral buckling strength of that segment.
Unlike hot-rolled shapes, cold-formed steel shapes are characterized by small wall thicknesses. As a
result, elements under compression can buckle locally at stresses much lower than the yield stress. To
approximate the non-uniform distribution of stresses in such compression elements the concept of an
effective width is used (AISI, 1989 and 1991). In this approach, the lightly stressed portion of the element is
assumed ineffective in resisting stresses. The stress distribution over the remaining portion is assumed to be
constant.
Figure 3.2 shows the effective widths of cold-formed steel shapes in bending. The effective width b of the
compression flange depends on the normal stress f in the flange, the flat-width-to-thickness ratio (X1/X4),
and the plate buckling coefficient. Figures 3.2a and 3.2b represent shapes with stiffened and unstiffened
compression flanges, respectively. The effective widths b1 and b2 of the web are a function of the maximum
compressive and tensile stresses f1 and f2 (Figure 3.2) and the flat-width-to-thickness ratio (X2/X4).
Considering the local buckling effects, for ASD and for LRFD where Se
is the effective section modulus, is the factor of safety in bending, b is the resistance factor
for bending strength (equal to 0.90 for I, Z, and all other shapes not braced throughout, and 0.95 for fully
braced hat shapes), and Fy is the yield stress of steel. The dependence of effective widths on stresses means
that Se (and other cross-sectional properties) cannot be calculated explicitly.