Professional Documents
Culture Documents
Sampling Theory 101: Oliver Kreylos
Sampling Theory 101: Oliver Kreylos
Uploaded by
Haitham Youssef0 ratings0% found this document useful (0 votes)
7 views60 pagesOriginal Title
SamplingTheory101.pdf
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
7 views60 pagesSampling Theory 101: Oliver Kreylos
Sampling Theory 101: Oliver Kreylos
Uploaded by
Haitham YoussefCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 60
Sampling Theory 101
Oliver Kreylos
kreylos@cs.ucdavis.edu
Center for Image Processing and Integrated Computing (CIPIC)
Department of Computer Science
University of California, Davis
CIPIC Seminar 11/06/02 – p.1
Outline
• Things that typically go wrong
• Mathematical model of sampling
• How to do things better
CIPIC Seminar 11/06/02 – p.2
Things That Typically Go Wrong
CIPIC Seminar 11/06/02 – p.3
Where Does Sampling Occur?
Almost all data we are dealing with is discrete
• Evaluation of sampled functions at arbitrary
sites
• Volume rendering
• Isosurface extraction
• Ray tracing
• ...
CIPIC Seminar 11/06/02 – p.4
What Went Wrong Here?
Typical ray tracing example:
CIPIC Seminar 11/06/02 – p.5
Sampling and Reconstruction
CIPIC Seminar 11/06/02 – p.6
Sampling and Reconstruction
CIPIC Seminar 11/06/02 – p.6
Sampling and Reconstruction
CIPIC Seminar 11/06/02 – p.6
Sampling and Reconstruction
• Undersampling?
• Sampling “below Nyquist rate”?
• Quick solution: Double sampling rate
CIPIC Seminar 11/06/02 – p.6
Sampling and Reconstruction
CIPIC Seminar 11/06/02 – p.6
Sampling and Reconstruction
• Things get better, but are still bad
• Isn’t sampling above the Nyquist rate
supposed to solve all problems?
CIPIC Seminar 11/06/02 – p.6
Sampling Theory
To understand what went wrong on the last slide,
we need a mathematical model of sampling.
CIPIC Seminar 11/06/02 – p.7
Mathematical Model of Sampling
CIPIC Seminar 11/06/02 – p.8
Choice of Domain
• Process of sampling and reconstruction is
best understood in frequency domain
• Use Fourier transform to switch between time
and frequency domains
• Function in time domain: signal
• Function in frequency domain: spectrum
CIPIC Seminar 11/06/02 – p.9
Fourier Transform I
• Many functions f : R → R can be written as
sums of sine waves
X
f (x) = aω sin(ωx + θω )
ω
• ω = 2π · frequency is angular velocity,
• aω is amplitude, and
• θω is phase shift
CIPIC Seminar 11/06/02 – p.10
Fourier Transform II
• Moving to complex numbers simplifies
notation:
cos(ωx) + i sin(ωx) = eiωx
(Euler identity )
• One complex coefficient cω eiωx encodes both
amplitude and phase shift
• Moving to integral enlarges class of
representable functions
CIPIC Seminar 11/06/02 – p.11
Fourier Transform III
• Now, for almost all f :
Z
f (x) = F (ω)eiωx dω
• F (ω) is the spectrum of f (x), and the above
operator is the inverse Fourier transform
• Its inverse, the Fourier transform, is
Z
F (ω) = f (x)e−iωx dx
CIPIC Seminar 11/06/02 – p.12
Some Signals and Their Spectra
Single sine wave f (x) = sin(ωx):
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Sum of two sine waves
f (x) = sin(ωx) + 0.5 sin(2ωx):
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Box function:
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Wider box function:
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Triangle function:
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Comb function:
CIPIC Seminar 11/06/02 – p.13
Some Signals and Their Spectra
Wider comb function:
CIPIC Seminar 11/06/02 – p.13
Convolution I
• The convolution operator is a generalized
formula to express weighted averaging of an
input signal f and a weight function or filter
kernel g:
Z
(f ∗ g)(x) = f (t) · g(x − t) dt
• One important application of convolution is
reconstructing sampled signals
CIPIC Seminar 11/06/02 – p.14
Convolution II
Z
(f ∗ g)(x0 ) = f (t) · g(x0 − t) dt
f f f
x0 x x0 x x0 x
g f f*g
x x0 x x0 x
CIPIC Seminar 11/06/02 – p.15
Convolution III
Linear interpolation can be interpreted as
convolution:
f f
x x
g f
x x
CIPIC Seminar 11/06/02 – p.16
Function Reconstruction
Constant interpolation:
CIPIC Seminar 11/06/02 – p.17
Function Reconstruction
Linear interpolation:
CIPIC Seminar 11/06/02 – p.17
Function Reconstruction
Catmull-Rom interpolation:
CIPIC Seminar 11/06/02 – p.17
Function Reconstruction
Cubic B-spline approximation:
CIPIC Seminar 11/06/02 – p.17
The Convolution Theorem
• The Convolution Theorem relates convolution
and Fourier transform:
(f ∗ g) ↔ F · G
• Convolutions can be computed by going
through the frequency domain:
(f ∗ g) = IFT(FT(f ) · FT(g))
CIPIC Seminar 11/06/02 – p.18
Sampling in Time Domain
• Sampling a function f means multiplying it
with a comb function c with tap distance d (or
sample frequency ω = 2π/d):
s=f ·c
• Reconstructing a sampled function means
convolving it with a suitable filter kernel
f0 = s ∗ k
• What happens to the function’s spectrum in
the process?
CIPIC Seminar 11/06/02 – p.19
Sampling in Frequency Domain
• The spectrum of s is the convolution of F
and C, the spectra of f and c
• C is a comb function with tap distance 2π/d
• S consists of shifted copies of F , each 2π/d
apart
CIPIC Seminar 11/06/02 – p.20
Sampling Process - Time Domain
CIPIC Seminar 11/06/02 – p.21
Sampling Process - Frequency Domain
CIPIC Seminar 11/06/02 – p.22
Sampling in Frequency Domain
• If the sampling frequency is ω, the replicated
copies of f ’s spectrum are ω apart
• If the highest-frequency component in f is ωf ,
f ’s spectrum covers the interval [−ωf , ωf ]
• If ωf ≥ ω/2, then the replicated spectra
overlap!
• This means, information is lost
CIPIC Seminar 11/06/02 – p.23
The Sampling Theorem
• “If f is a frequency-limited function with
maximum frequency ωf , then f must be
sampled with a sampling frequency larger
than 2ωf in order to be able to exactly
reconstruct f from its samples.”
• This theorem is sometimes called Shannon’s
Theorem
• 2ωf is sometimes called Nyquist rate
CIPIC Seminar 11/06/02 – p.24
Reconstruction
• The only difference between F and S is that S
is made of shifted copies of F
• If those extra, higher-frequency, spectra could
be removed from S, f would “magically”
reappear
• Reconstructing f means low-pass-filtering s!
CIPIC Seminar 11/06/02 – p.25
Reconstruction Process - Frequency Dom
CIPIC Seminar 11/06/02 – p.26
Reconstruction Process - Time Domain
CIPIC Seminar 11/06/02 – p.27
Reconstruction Problem
• Practical problem: The optimal reconstruction
filter, the sinc function, has infinite support
• Evaluating it in the time domain involves
computing a weighted average of infinitely
many samples
• Practical reconstruction filters must have finite
support
• But: A perfect low-pass filter with finite
support does not exist!
CIPIC Seminar 11/06/02 – p.28
The Quest For Better Filters
CIPIC Seminar 11/06/02 – p.29
Commonly Used Filters
Constant filter:
CIPIC Seminar 11/06/02 – p.30
Commonly Used Filters
Linear filter:
CIPIC Seminar 11/06/02 – p.30
Commonly Used Filters
Catmull-Rom filter:
CIPIC Seminar 11/06/02 – p.30
Commonly Used Filters
B-Spline filter:
CIPIC Seminar 11/06/02 – p.30
Sampling Theory Filters
Truncated sinc filter:
CIPIC Seminar 11/06/02 – p.31
Sampling Theory Filters
Lanczos filter:
CIPIC Seminar 11/06/02 – p.31
Sampling Theory Filters
Full sinc filter:
CIPIC Seminar 11/06/02 – p.31
Sampling Theory Applications
CIPIC Seminar 11/06/02 – p.32
Function Reconstruction
• Sampling theory filters (Lanczos etc.) can be
used to reconstruct n-dimensional functions
sampled on regular grids
• Oversampling improves reconstruction quality
with “bad” filters, but at a high cost
CIPIC Seminar 11/06/02 – p.33
Function Resampling
• When resampling a sampled function to a
different grid (shifted and/or scaled), it is
important to use a good reconstruction filter
• When downsampling a function, it is
important to use a good low-pass filter to cut
off frequencies above half the new sampling
frequency
CIPIC Seminar 11/06/02 – p.34
Volume Rendering
• Basic question: How many samples to take
per cell?
CIPIC Seminar 11/06/02 – p.35
Volume Rendering
• Basic question: How many samples to take
per cell?
• Sampling theory says “1,” but integration
along ray might demand more
CIPIC Seminar 11/06/02 – p.35
Ray Tracing
• In ray tracing, the function to be sampled is
typically not frequency-limited
• Practical solution: Shoot multiple rays per
pixel (oversampling) and sample down to
image resolution
• Using a good low-pass filter is important
CIPIC Seminar 11/06/02 – p.36
Ray Tracing
CIPIC Seminar 11/06/02 – p.36
Conclusions
CIPIC Seminar 11/06/02 – p.37
Conclusions
• Knowing the mathematical background of
sampling and reconstruction helps to
understand common problems and devise
solutions
• Ad-hoc solutions usually do not work well
• This stuff should be taught in class!
CIPIC Seminar 11/06/02 – p.38
The End
CIPIC Seminar 11/06/02 – p.39
You might also like
- D 1875 - 03 Rde4nzuDocument2 pagesD 1875 - 03 Rde4nzuMarcelo100% (1)
- Lecture 4 Day 3 Stochastic Frontier AnalysisDocument45 pagesLecture 4 Day 3 Stochastic Frontier Analysistrpitono100% (1)
- A Chemical Plant Produces Oxygen by Liquefying Air and Separating It Into Its Component Gases by Fractional DistillationDocument2 pagesA Chemical Plant Produces Oxygen by Liquefying Air and Separating It Into Its Component Gases by Fractional DistillationVIKRAM KUMARNo ratings yet
- Rice 0433Document29 pagesRice 0433Gustavo de carvalhoNo ratings yet
- Future DevelopmentsDocument15 pagesFuture DevelopmentsZen KyoNo ratings yet
- 7 - Freeway Traffic ControlDocument6 pages7 - Freeway Traffic ControlDr. Ir. R. Didin Kusdian, MT.No ratings yet
- Microstructure-Properties: II The KJMA Equation: 27-302 Fall, 2002 Prof. A. D. RollettDocument27 pagesMicrostructure-Properties: II The KJMA Equation: 27-302 Fall, 2002 Prof. A. D. RollettIbrahim HasanNo ratings yet
- CS6640 F2014 Fourier I PDFDocument39 pagesCS6640 F2014 Fourier I PDFAya MohmmedNo ratings yet
- Modeling Multi-Phase Flows in OpenfoamDocument28 pagesModeling Multi-Phase Flows in OpenfoamPravin Kumar SharmaNo ratings yet
- LSyn3 UnateDocument23 pagesLSyn3 UnateSRIKRISHNA.SCUNo ratings yet
- Outline: SamplingDocument43 pagesOutline: Samplingdjoseph_1No ratings yet
- 5b DanaDocument67 pages5b Dana22 / Gyanaranjan NayakNo ratings yet
- CS 294-73 Software Engineering For Scientific Computing Lecture 16: Multigrid (Structured Grids Revisited)Document32 pagesCS 294-73 Software Engineering For Scientific Computing Lecture 16: Multigrid (Structured Grids Revisited)Edmund ZinNo ratings yet
- Lecture-3 Modeling of Translational Mechanical SystemsDocument23 pagesLecture-3 Modeling of Translational Mechanical SystemsMuneeb JawaidNo ratings yet
- Nesterov CD 2012Document23 pagesNesterov CD 2012bzsahilNo ratings yet
- Particle-FilteringDocument8 pagesParticle-Filteringapi-3855364No ratings yet
- Boundary Condition Calculation Procedures For Inviscid Supersonic Flow Fields (1973) PDFDocument20 pagesBoundary Condition Calculation Procedures For Inviscid Supersonic Flow Fields (1973) PDFSamuelNo ratings yet
- The Derivative: ObjectivesDocument11 pagesThe Derivative: ObjectivesHà PhạmNo ratings yet
- LN2 2021Document31 pagesLN2 2021oanh nguyen pham oanhNo ratings yet
- Filtering Images in The Frequency DomainDocument25 pagesFiltering Images in The Frequency DomainSimrandeep SinghNo ratings yet
- Ch10-1 (FIR Filter Design) UDocument33 pagesCh10-1 (FIR Filter Design) UphithucNo ratings yet
- MFE 1 Week 4 SlidesDocument46 pagesMFE 1 Week 4 SlidesSangheon SongNo ratings yet
- Wolfe, Markov Chain in Linear ProgrammingDocument10 pagesWolfe, Markov Chain in Linear Programmingcarlitos11evildarkNo ratings yet
- CS-6777 Liu AbsDocument103 pagesCS-6777 Liu AbsILLA PAVAN KUMAR (PA2013003013042)No ratings yet
- Progress in Linear Programming Based Branch-and-Bound AlgorithmsDocument56 pagesProgress in Linear Programming Based Branch-and-Bound AlgorithmsHanifah HanumNo ratings yet
- Canonical Signed Digits (CSD)Document5 pagesCanonical Signed Digits (CSD)Dr. Sampatrao L PinjareNo ratings yet
- Frequently Asked Questions On Wavelets: Q1. What Is The Wavelet Transform?Document10 pagesFrequently Asked Questions On Wavelets: Q1. What Is The Wavelet Transform?AndyBasuNo ratings yet
- Chapter 6 - Part 2Document30 pagesChapter 6 - Part 2Dan ARikNo ratings yet
- 8654 19.photocurrentDocument11 pages8654 19.photocurrentMuhammad Maiz GhauriNo ratings yet
- Math 2400 Lecture Notes: Differentiation: Pete L. ClarkDocument33 pagesMath 2400 Lecture Notes: Differentiation: Pete L. ClarkEGE ERTENNo ratings yet
- 10W12-13Ch10 Quantitative ModelsDocument62 pages10W12-13Ch10 Quantitative ModelsNoob Minecrafter KevinNo ratings yet
- Spectral TechniquesDocument42 pagesSpectral TechniquesHIMANI NARAIN HIMANI NARAINNo ratings yet
- Conic Programming in GAMSDocument36 pagesConic Programming in GAMSamirehosseinNo ratings yet
- Lab Manual CDocument42 pagesLab Manual CGumnam BandaNo ratings yet
- Complex gnc05 PDFDocument17 pagesComplex gnc05 PDFVignesh RamakrishnanNo ratings yet
- The Comparison of The Effect of Haimming Window AnDocument6 pagesThe Comparison of The Effect of Haimming Window AnAyushi NaikNo ratings yet
- A Real-Time Implementation of Fpga Hardware For Mpeg Artifact Reduction For Video ApplicationsDocument5 pagesA Real-Time Implementation of Fpga Hardware For Mpeg Artifact Reduction For Video ApplicationsCharoensakNo ratings yet
- Wavelet Shrinkage: Asymptopia?: David L. Donoho, Iain M. Johnstone, Gerard Kerkyacharian, Dominique PicardDocument45 pagesWavelet Shrinkage: Asymptopia?: David L. Donoho, Iain M. Johnstone, Gerard Kerkyacharian, Dominique PicardAnand MattadNo ratings yet
- Real-Time FIR Digital FiltersDocument56 pagesReal-Time FIR Digital FiltersullisrinuNo ratings yet
- Computer Architecture - Tutorial 2 (TUTOR COPY) : Context, Objectives and OrganizationDocument5 pagesComputer Architecture - Tutorial 2 (TUTOR COPY) : Context, Objectives and OrganizationHalim KorogluNo ratings yet
- Lec 23Document4 pagesLec 23abdurahman saeedNo ratings yet
- Immersed Boundary Training Slides OFW7Document29 pagesImmersed Boundary Training Slides OFW7AndreaNo ratings yet
- Unit 4 Differentition and CalculusDocument35 pagesUnit 4 Differentition and CalculusPriscilla MuyakoNo ratings yet
- Dat Astruc TDocument31 pagesDat Astruc Tammayi9845_930467904No ratings yet
- T0406 PaperDocument7 pagesT0406 PaperJosue AzurinNo ratings yet
- Basics of Monte Carlo Simulation: Condensed From A Presentation by M. AsaiDocument40 pagesBasics of Monte Carlo Simulation: Condensed From A Presentation by M. AsaiMohan RjNo ratings yet
- Graph Signal ProcessingDocument56 pagesGraph Signal Processingale3265No ratings yet
- 08 - Delta Sigma PDFDocument20 pages08 - Delta Sigma PDFAmy BarryNo ratings yet
- Lecture 16 FIR DesignDocument28 pagesLecture 16 FIR DesignevhyajahNo ratings yet
- 3rd LE-Nonlinear Programming - 30april2019Document12 pages3rd LE-Nonlinear Programming - 30april2019Mayumi VillavicencioNo ratings yet
- ConnumincatuonDocument88 pagesConnumincatuonSanjai RadhakrishnanNo ratings yet
- Nipsdlufl10 RandomWeights PDFDocument9 pagesNipsdlufl10 RandomWeights PDFÜmit AslanNo ratings yet
- OFDM Basics 1Document28 pagesOFDM Basics 1sreedeviishNo ratings yet
- Chapter 7 - RecursionDocument23 pagesChapter 7 - RecursionTanveer Ahmed HakroNo ratings yet
- Raycasting: Direct Volume RenderingDocument6 pagesRaycasting: Direct Volume RenderingCarlos FernandezNo ratings yet
- Konveksna OptimizacijaDocument179 pagesKonveksna OptimizacijaVladimir StojanovićNo ratings yet
- Tr0710 WangDocument20 pagesTr0710 WangAugustoZebadúaNo ratings yet
- Lab 10 (Oscilloscope)Document3 pagesLab 10 (Oscilloscope)thissisnateNo ratings yet
- Constrained Curve and Surface Fitting: Simon FL OryDocument51 pagesConstrained Curve and Surface Fitting: Simon FL OryLim AndrewNo ratings yet
- Advanced Control of A Reactive Distillation ColumnDocument7 pagesAdvanced Control of A Reactive Distillation ColumnMahesh ChantarkarNo ratings yet
- 9th Physics FloatationDocument4 pages9th Physics FloatationMuzaFar100% (1)
- Đề Thi Chọn HSG Tiếng Anh 12 Năm 2018 - 2019 Cụm Gia Bình - Lương Tài - Bắc NinhDocument8 pagesĐề Thi Chọn HSG Tiếng Anh 12 Năm 2018 - 2019 Cụm Gia Bình - Lương Tài - Bắc Ninhnhianh2512No ratings yet
- Tutorial For MASTAN2: Ronald D. ZiemianDocument68 pagesTutorial For MASTAN2: Ronald D. ZiemianGelique de CastroNo ratings yet
- Cention NDocument14 pagesCention NGiTa TAriganNo ratings yet
- Sampling BP Proakis2007Document12 pagesSampling BP Proakis2007santosh1122No ratings yet
- Walker and Goulas - Perf Characteristics of Pumps Handling Non-Newtonian Slurries - IMechE 1984Document9 pagesWalker and Goulas - Perf Characteristics of Pumps Handling Non-Newtonian Slurries - IMechE 1984Cristian RANo ratings yet
- Revised Basis Sets For The LANLDocument3 pagesRevised Basis Sets For The LANLFadjar MulyaNo ratings yet
- Documents - Tips Biela-CatiaDocument35 pagesDocuments - Tips Biela-CatiaBaiatu' De Pe ArgesNo ratings yet
- Atmosphere Basics WebsquestDocument2 pagesAtmosphere Basics Websquestapi-264100173No ratings yet
- Module 2Document8 pagesModule 2Ashner NovillaNo ratings yet
- Exstik Fl700: User GuideDocument11 pagesExstik Fl700: User GuideTogoYouredNo ratings yet
- Expt-9 Measurement of FluorideDocument26 pagesExpt-9 Measurement of FluorideYogendra PatilNo ratings yet
- Ch01-Slides-1 Gas LawsDocument60 pagesCh01-Slides-1 Gas LawsDoreen BenezethNo ratings yet
- Sony dcr-trv250 Adjustment Ver-1.2 PDFDocument92 pagesSony dcr-trv250 Adjustment Ver-1.2 PDFRevnic FlorinNo ratings yet
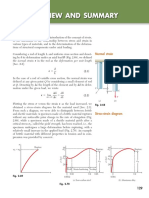
- Review and Summary: Normal StrainDocument6 pagesReview and Summary: Normal StrainkakatangNo ratings yet
- Basic Syllogistic Logics: Larry Moss, Indiana UniversityDocument75 pagesBasic Syllogistic Logics: Larry Moss, Indiana UniversityHectorNo ratings yet
- 04MA246EX Ran PDFDocument15 pages04MA246EX Ran PDFznchicago338No ratings yet
- 19.ergonomic Assessment of Manual Material - EncDocument9 pages19.ergonomic Assessment of Manual Material - EncMuthu BaskaranNo ratings yet
- An Introduction To ObserversDocument7 pagesAn Introduction To Observersapi-3826450No ratings yet
- 112 Experiment 4Document3 pages112 Experiment 4Abhishek KunduNo ratings yet
- Tunnel Structures Seismic DesignDocument12 pagesTunnel Structures Seismic DesignIbis TelloNo ratings yet
- Reinforced Liquid Coating Encapsulation Products For Leaded Paint in BuildingsDocument6 pagesReinforced Liquid Coating Encapsulation Products For Leaded Paint in BuildingsAhmad Zubair RasulyNo ratings yet
- Valentine Microrheology PresentationDocument10 pagesValentine Microrheology PresentationAhmed El KaffasNo ratings yet
- Catalogo Notifier 8Document2 pagesCatalogo Notifier 8Ali HadiNo ratings yet
- Health Index CalculationDocument7 pagesHealth Index CalculationManinder ChoudharyNo ratings yet
- 2001 Paper 2 NovDocument12 pages2001 Paper 2 Novrajdeepghai5607No ratings yet
- VFM - Manual 1-1Z301113040Document23 pagesVFM - Manual 1-1Z301113040Rajagopal SNo ratings yet
- NACA TN-3273 Compressibility Factor For SteamDocument62 pagesNACA TN-3273 Compressibility Factor For SteamR LNo ratings yet