246 Cb.

5 Mott Insulators

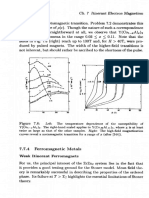
The argument for subtracting the d-bandwidth wd is the same that we

used for Fig. 4.8: we have created a quasi-particle ( P S I and
) a quasi-
hole (dn-l)which can propagate on the background of d" ions with the
d-electron hopping amplitudes, broadening the levels into subbands.
The p - d charge transfer process (Fig. 5.9, right) costs primarily
Apd = & - ep, where zd is the center of the upper Hubbard subband. To
get the activation energy, this has to be corrected for the broadening of
the quasi-particle, and quasi-hole, levels into bands:

A, Apd - wp -k wd (5.82)
2
whereby the contribution due to the large p-bandwidth is essential.

dn+1p

dn-dn u- fP-P A
MOTT INSULATOR CHARGE TRANSFER INS.

Figure 5.10: Excitation spectra of d - d and p - d type charge transfer processes

in Mott insulators (left), and charge transfer insulators (right). p signifies a phole.

Though Fig. 5.8 looks as if it were about ordinary bands, it has

to be used with great caution because what it really shows are spectra
of itinerant many-electron excitations. If we prefer to be more circum-
spect [348], we have to redraw the diagrams as shown in Fig. 5.10. In
contrast to 5.8 with its filled or empty bands, the ground state is rep-
resented here as the dispersionless level 8 4 . This corresponds to our
intuitive notion of a rigid Mott-localized state. It is a quite different
matter that excited particles (and holes) propagate and have a finite