Professional Documents
Culture Documents
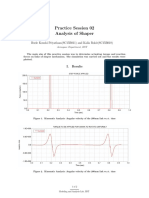
Lab Report 3
Uploaded by
Shivalik NaikCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Lab Report 3
Uploaded by
Shivalik NaikCopyright:
Available Formats
Pressure distribution over an airfoil
Ajay Kumar Meena, Alok Kumar Gartia , Narendra Kumar Meena,
L Shivalik Naik , Uttam Jodawat , Akash Kanaujiya
Department of Aerospace, Indian Institute of Space Science and Technology
The experiment was a study on the lift and drag coefficients from the pressure distribu-
tion over an airfoil of NACA series 662-015 in a wind tunnel run. The same was compared
with the XFLR5 results. Though these were comparable, they were not exactly same as
the experimental datas were taken only for finite number of points on the arfoil.
Nomenclature
P Pressure, N/m2
τ̄¯ Shear tensor, N/m2
N Normal force, N
A Axial force, N
CL Coefficient of lift
CD Coefficient of drag
q Dynamic pressure, N/m2
◦
θ Angle between chord and resultant force,
α Angle of attack, ◦
Subscript
∞ Freestream
i Index
u Upper surface of aerofoil
l Lower surface of aerofoil
I. Introduction
In this experiment, an open suction wind tunnel operating at lower pressures is used to measure the
static pressure at various points on an aerofoil. Since the Mach no. of the flow is low, it can be assumed
to be incompressible. Stall angle, the angle at which flow separation (fluid flow detaches from the object
and eddies and vortices are formed) occurs was measured at various Reynolds number. Turbulent flow has
lesser tendency to separate because of higher energy to molecules nearer to the surface. However, the flow
over the airfoil is laminar under the conditions of operation of the wind tunnel. Flow separation reduces lift
and increases drag and so is a important phenomenon to be dealt with. Assuming inviscid flow, the pressure
distribution is used to measure the lift and drag acting on the air foil. CL and CD are calculated for various
Reynolds number and compared.
II. Theory
Consider a small portion of the aerofoil that can be considered as a straight line with unit length and
area dS and over which the surface forces can be assumed constant. Thus, the force on this small area is
¯ = −P dS
dF ¯ + τ̄¯.dS
¯
Neglecting viscous effects, and resolving the force into axial and normal components for the entire aerofoil
(Fig. 1),
1 of 9
American Institute of Aeronautics and Astronautics
Figure 1. Figure showing the pressure and shear forces acting on the upper and lower surface of the airfoil.
Z TE
N= (−Pu dSu cosθ + Pl dSl cosθ)
LE
Z TE
A= (−Pu dSu sinθ + Pl dSl sinθ)
LE
Since, the integral requires pressure at each and every point on the aerofoil, it is not possible to calculate
directly. It can however be approximated by polygonizing the aerofoil and assuming the force to be constant
on each of the sides of the polygon. Thus,
p
dSi = (yi − yi+1 )2 + (xi − xi+1 )2
And the forces are calculated using,
X
N= Pl(avg) cosθdSi − Pu(avg) cosθdSi
i
X
A= Pl(avg) sinθdSi − Pu(avg) sinθdSi
i
Now, the lift and drag can be calculated as
L = N cosα − Asinα
D = N sinα + Acosα
where α is the angle of attack of the aerofoil. The coefficient of lift, CL and coefficient of drag CD are given
by,
L
CL =
q∞ Splan
D
CD =
q∞ Splan
2 of 9
American Institute of Aeronautics and Astronautics
III. Experimental Setup
The experiment was performed on a suction type wind tunnel. The aerofoil to be tested is kept in the
test section with static pressure probes attached to various points on the aerofoil. A variable inclination
multi-tube manometer with ethanol as the manometric fluid, is used to measure the pressures.
IV. Procedure
1. The ambient temperature and pressure were noted down.
2. The multi-tube manometer was checked, the angle of inclination was noted and the probes connected
to various sections of importance were noted.
3. The motor was switched on. It was ensured that the blades of the fan was rotating in the same direction
as marked.
4. The RPM was slowly increased to 760 RPM by rotation the knob on the potentiometer.
5. The angle of attack was of the aerofoil was kept at -6◦ .
6. The manometer measurements were noted down and measurements were taken for increments of angle
of attack (in 3◦ steps) till stall is reached. The onset of stall is indicated by a sudden change in the
manometer readings.
7. This was repeated for different RPMs.
8. The RPM of the motor was brought down slowly and the motor was switched off.
V. Result and Discussion
It can be observed that a linear relationship exists between Lift and Angle of Attack(AoA) over some
range of AoA, uptil the Critical Angle of Attack(αc ), where the maximum lift or lift coefficient is obtained.
As AoA increases, near to the Critical AoA(αc ), the simple linear relationship between lift and AoA breaks
down. Also, beyond the c, any increase in AoA is accompanied by a decrease in lift along with a simultaneous
decrease in lift coefficient. This observation can be attributed to the drastic increase in adverse pressure
gradient which causes ow separation.
It was also observed that for zero AoA, a non-zero residue of lift existed, which is characteristic of an
asymmetric airfoil (in this case NACA 662 015). Thus by varying the AoA of the airfoil, the stall angle
was determined to be equal to 11.7 deg. The experimental results are compared with the results obtained
from ow simulation software XFLR5. The drag vs graph shows that the drag is increasing with the angle
of attack for a particular velocity. Similarly the coefficient of drag vs α follows the same trend.
3 of 9
American Institute of Aeronautics and Astronautics
Figure 2. Lift vs Angle of attack
CL
Figure 3. CD
vs Angle of attack
4 of 9
American Institute of Aeronautics and Astronautics
Figure 4. CL vs Angle of attack
Figure 5. Drag vs Angle of attack
5 of 9
American Institute of Aeronautics and Astronautics
Figure 6. CD vs Angle of attack
Figure 7. Xflr analysis for 700 RPM
6 of 9
American Institute of Aeronautics and Astronautics
VI. Conclusion
Slight deviation of results from the theoretical values obtained using xr was observed. This is due to
the method of calculation that was considered to nd the values of lift and drag where average pressure has
been considered over a nite surface area to calculate magnitude of force acting over it. These deviations are
also due to the manufacturing defects where perfectly symmetric airfoil cannot be obtained. The airfoil was
already placed at a positive angle of attack due to which negative lift was not obtained.
In this experiment, lift was calculated by integrating the pressure on the walls of the airfoil (not very
far above or below the airfoil over a long enough length). This method is very convenient to measure and
calculate lift as well as drag. The lift and the coefficient of lift varied linearly with the angle of attack. The
CL vs α characteristics were same for dierent V.
VII. Appendix
A. Sample Calculations
Calculation of Atmospheric pressure:
Pbarometer × 101325
Pa = Pa
760
750 × 101325
Pa = = 99991.7763Pa
760
Calculation of pressure at any point on the airfoil:
Pi = Pa − (ρet ) × g × (hi − href ) × 10−2 × sin45◦
For RP M = 600 α = 4◦ i=2
h2 = 9.8
h3 = 9.5
P2 = 99991.77632 − (789) × 9.81 × (10.1 − 6.7) × 10−2 × 0.5 = 99685.33066Pa
The pressure at (i + 1)th point is found using the above relation.
So, P3 = 99701.74739Pa
The average between two points is defined by:
Pi + Pi+1
Pavgi = (1)
2
So, Pavg2 = 99693.53902 Pa
The X and Y locations of the probe points 5 and 6 are:
X2 = 0.01980198
X3 = 0.03960396
Y2 = 0.002
Y3 = 0.004
=⇒ dx = 0.01980198
dy = 0.002
7 of 9
American Institute of Aeronautics and Astronautics
Calculating the forces:
N = Pavgi × dx
N = 99693.53902 × 0.01980198 = 1974.129466 N
A = Pavgi × dy
A = 99693.53902 × 0.002 = 199.387078N
L = N cosα − Asinα (2)
D = N sinα + Acosα (3)
Substituting the above values in equation 2 and 3:
L = 1974.129466 × cos4◦ − 199.387078 × sin4◦
L = 1955.412046N
D = 1974.129466 × sin4◦ + 199.387078 × cos4◦
D = 336.6096096914N
Computing ρ :
From the state equation
Pa = ρ × R × T (4)
Pa
=⇒ ρ =
R×T
99991.77632
ρ= = 1.1498kg/m3
287 × 304
Uncertainty Analysis
RP M = 600
α = 4◦
Taking partial derivate of equation 2 and equation 3 with respect to the variables:
1. α
2. N
3. A
∂L
= cosα (5)
∂N
∂L
= −N sinα − Acosα (6)
∂α
∂L
= −sinα (7)
∂A
8 of 9
American Institute of Aeronautics and Astronautics
r
∂L ∂L ∂L
UL = ( ∂N )2 + ( ∂α)2 + ( ∂A)2 = (8)
∂N ∂α ∂A
∂D
= sinα (9)
∂N
∂D
= N cosα − Asinα (10)
∂α
∂D
= −sinα (11)
∂A
r
∂D ∂D ∂D
UD = ( ∂N )2 + ( ∂α)2 + ( ∂A)2 = (12)
∂N ∂α ∂A
∂CL 2
= (13)
∂L ρV 2 S
∂CL −1
= (14)
∂ρ ρCD
∂CL −2
= (15)
∂v Cl V
r
∂CL ∂CL ∂CL
UCL = ( ∂N )2 + ( ∂α)2 + ( ∂A)2 = 0.013636562 (16)
∂N ∂α ∂A
∂CD 2
= (17)
∂L ρV 2 S
∂CD −1
= (18)
∂ρ ρCD
∂CD −2
= (19)
∂v CD V
r
∂CD ∂CD ∂CD
UCD = ( ∂N )2 + ( ∂α)2 + ( ∂A)2 = 0.001790313 (20)
∂N ∂α ∂A
B. B. Calculation Table
The entire calculation table was done excel sheet. Excel sheet was not compatible for entire readings, hence
a separate file is attached with this report.
9 of 9
American Institute of Aeronautics and Astronautics
VIII. Acknowledgements
We would like to thank our supervisor, Prof. Manoj T. Nair and Prof. Pradeep Kumar P., for the
patient guidance, encouragement. We would like to thank lab Assistants Mr. Nasaruddeen sir and especially
Navneet from M.tech for guiding us in carrying out and verifying experiments results.
References
1 Abbott, I. H., and von Doenhoff, A. E., Theory of wing sections, including a summary of Airfoil data, McGraw-Hill, 1949.
2 Anderson, J. D., Fundamentals of Aerodynamics, 5th edition, Tata McGraw-Hill Education, 2010.
3 The flight demonstration wind tunnel, Users Manual.
4 http://www.xflr5.com/xflr5.htm
5 http://web.mit.edu/drela/Public/web/xfoil/
10 of 9
American Institute of Aeronautics and Astronautics
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- HTTPHRM - Iimb.ernet - iniimbPGP BA 2022welcome - Aspname1 L20SHIVALIK20NAIK&srno1 21212173&email Shiva - Shivalik37@gmail - Com&Document1 pageHTTPHRM - Iimb.ernet - iniimbPGP BA 2022welcome - Aspname1 L20SHIVALIK20NAIK&srno1 21212173&email Shiva - Shivalik37@gmail - Com&Shivalik NaikNo ratings yet
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- InstructionsDocument1 pageInstructionsShivalik NaikNo ratings yet
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- HR QuestionsDocument1 pageHR QuestionsShivalik NaikNo ratings yet
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- Unsc GuideDocument21 pagesUnsc GuideShivalik NaikNo ratings yet
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Assignment 2 MPMDocument2 pagesAssignment 2 MPMShivalik NaikNo ratings yet
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- AE Lab Template BasicDocument2 pagesAE Lab Template BasicShivalik NaikNo ratings yet
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Introduction To Shadowgraph and Schlieren Imaging: RIT Scholar WorksDocument59 pagesIntroduction To Shadowgraph and Schlieren Imaging: RIT Scholar WorksAnmar HamidNo ratings yet
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Soil Mechanics PowerpointDocument239 pagesSoil Mechanics PowerpointEdcel Angelo TomasNo ratings yet
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- Abb Sas GeneralDocument43 pagesAbb Sas Generalsabill arasyidNo ratings yet
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- Friction Clutches PDFDocument14 pagesFriction Clutches PDFamanmittal0850% (2)
- IEEE and IEC StandardsDocument11 pagesIEEE and IEC StandardschupzptNo ratings yet
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Practical Exercise 2 - SolutionDocument5 pagesPractical Exercise 2 - SolutionmidoriNo ratings yet
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- A Quick Tutorial On RSLogix Emulator 5000Document9 pagesA Quick Tutorial On RSLogix Emulator 5000slavezerorjNo ratings yet
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Ekg 8Document2 pagesEkg 8Arun SNo ratings yet
- Geomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)Document2 pagesGeomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)ابوالحروف العربي ابوالحروفNo ratings yet
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Immediate Settlement Analysis Using Finite Element Analysis Models of Fb-MultipierDocument22 pagesImmediate Settlement Analysis Using Finite Element Analysis Models of Fb-MultipierRaaf RifandiNo ratings yet
- Cswip Appendix 01Document23 pagesCswip Appendix 01Nsidibe Michael EtimNo ratings yet
- D 880 - 92 R97 Rdg4mc05mli5nw - PDFDocument4 pagesD 880 - 92 R97 Rdg4mc05mli5nw - PDFomar alvaradoNo ratings yet
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Astm D 3341Document4 pagesAstm D 3341Manuel GuzmanNo ratings yet
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Fmaths 3RD Term YR11 PlanDocument28 pagesFmaths 3RD Term YR11 Planadegunloye temitopeNo ratings yet
- SharePoint 2010 QuestionsDocument5 pagesSharePoint 2010 QuestionsSreedhar KonduruNo ratings yet
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- CATL 37V 50ah Lithium Ternary Battery Cell - LiFePO4 BatteryDocument4 pagesCATL 37V 50ah Lithium Ternary Battery Cell - LiFePO4 BatterymlutfimaNo ratings yet
- Tutorial 1 PDFDocument2 pagesTutorial 1 PDFSYAFIQAH ISMAIL100% (1)
- TransistorDocument1 pageTransistorXhaNo ratings yet
- Tractor Engine and Drawbar PerformanceDocument3 pagesTractor Engine and Drawbar PerformancemaureenNo ratings yet
- Abstract of Talk by Dr. Nitin Oke For National Conference RLTDocument2 pagesAbstract of Talk by Dr. Nitin Oke For National Conference RLTnitinNo ratings yet
- OPTICast BrochureDocument2 pagesOPTICast BrochureIndra Pratap SengarNo ratings yet
- EX - NO:1a Data Definition Languages (DDL) Commands of Base Tables and ViewsDocument44 pagesEX - NO:1a Data Definition Languages (DDL) Commands of Base Tables and Viewslalit thakur100% (1)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Cross-Cultural Validation of The Scales For Outcomes in Parkinson's Disease-Psychosocial Questionnaire (SCOPA-PS) in Four Latin American CountriesDocument7 pagesCross-Cultural Validation of The Scales For Outcomes in Parkinson's Disease-Psychosocial Questionnaire (SCOPA-PS) in Four Latin American Countriesfozia hayyatNo ratings yet
- V-RAY 2.0 Option Editor Overview (SketchUp)Document14 pagesV-RAY 2.0 Option Editor Overview (SketchUp)thonethoneNo ratings yet
- Soil Bearing Capacity CalculationDocument29 pagesSoil Bearing Capacity CalculationJohn Jerome TerciñoNo ratings yet
- PHP Question AnswerDocument20 pagesPHP Question AnswerManish SharmaNo ratings yet
- Pages À Partir de Hyundai-Terracan-2001-2007-factory-service-manualDocument10 pagesPages À Partir de Hyundai-Terracan-2001-2007-factory-service-manualcointoinNo ratings yet
- GTB-BOL VetrificadoDocument19 pagesGTB-BOL VetrificadoelduenoNo ratings yet
- Tutorial Book 0.4Document27 pagesTutorial Book 0.4TonyandAnthonyNo ratings yet
- As 400Document70 pagesAs 400Radhakrishnan KandhasamyNo ratings yet
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)