Professional Documents
Culture Documents
IGCS Transformation PDF
IGCS Transformation PDF
Uploaded by
sabenasuhaimiOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
IGCS Transformation PDF
IGCS Transformation PDF
Uploaded by
sabenasuhaimiCopyright:
Available Formats
IGCSE - Extended Mathematics Transformation
Content:
Reflection (M): Reflect simple plane figures in horizontal or vertical lines;
Rotation (R): Rotate simple plane figures about the origin, vertices or midpoints of edges of the figures,
through multiples of 90°;
Enlargement (E) : Construct given translations and enlargements of simple plane figures;
Shear (H) &Stretch (S)
Their combinations (if M(a) = b and R(b) = c the notation RM(a) = c will be used;
Invariants under these transformations may be assumed.) Identify and give precise descriptions of
transformations connecting given figures.
Describe transformations using co-ordinates and matrices (singular matrices are excluded).
Transformation:
The word” transform “means "to change." In geometry, a transformation changes the position of a shape on a
coordinate plane. That means a shape is moving from one place to another.
The original shape of the object is called the pre-image and the final shape and position of the object is the image
under the transformation.
Isometry : Isometric transformation is a transformation that preserves congruence. In other words, a transformation in
which the image and pre-image have the same side lengths and angle measurements. The following transformations
maintain their mathematical congruence Reflection (Flip) ,Translation (Slide), Rotation (Turn).
Mathelaureate / IGCSE / Transformation / D.J Page no: 1
Transformation
Effect ( Image )
Matrix Example
1. Identity
No Effect , Image Remains Same
Matrix
This transformation matrix is the identity
matrix. When multiplying by this matrix, the
= =
point matrix is unaffected and the new matrix
is exactly the same as the point matrix.
2. Reflection Reflection in the X axis
This transformation matrix creates a
reflection in the x-axis. When multiplying by
this matrix, the x co-ordinate remains = =
unchanged, but the y co-ordinate changes
sign.
Mathelaureate / IGCSE / Transformation / D.J Page no: 2
3. Reflection Reflection in the Y axis
This transformation matrix creates a
reflection in the y-axis. When multiplying by
this matrix, the y co-ordiante remains = =
unchanged, but the x co-ordinate changes
sign.
4. Rotation 180 degrees Rotation
This transformation matrix creates a rotation
of 180 degrees. When multiplying by this
matrix, the point matrix is rotated 180 = =
degrees around (0,0). This changes the sign of
both the x and y co-ordinates.
5. Reflection Reflection on y = x line
This transformation matrix creates a
reflection in the line y=x. When multiplying by = =
this matrix, the x co-ordinate becomes the y
co-ordinate and the y-ordinate becomes the x
co-ordinate.
Mathelaureate / IGCSE / Transformation / D.J Page no: 3
6. Rotation 90 degrees clock wise rotation
This transformation matrix rotates the point
= =
matrix 90 degrees clockwise. When
multiplying by this matrix, the point matrix is
rotated 90 degrees clockwise around (0,0).
7. Rotation Anti-clockwise rotation 90 degrees
This transformation matrix rotates the point
matrix 90 degrees anti-clockwise. When
multiplying by this matrix, the point matrix is =
rotated 90 degrees anti-clockwise around
(0,0).
8. Reflection Reflection in the line y = -x
This transformation matrix creates a
reflection in the line y=-x. When multiplying = =
by this matrix, the point matrix is reflected in =
the line y=-x changing the signs of both co-
ordinates and swapping their values.
Mathelaureate / IGCSE / Transformation / D.J Page no: 4
9 .Enlargement Enlargement of scale factor
This transformation matrix is the identity
matrix multiplied by the scalar 6. When
multiplying by this matrix, the point matrix is = =
enlarged by a factor of 6 in the x and y
directions.
10.Enlargment
This transformation matrix is the identity
matrix but T1,1has been enlarged by a factor of
7 and T2,2 has been enlarged by a factor of 0.
= =
When multiplying by this matrix, the x co-
ordinate is enlarged by a factor of 7, whilst
the y co-ordinate is enlarged by a factor of 0.
11. Enlargment
This transformation matrix is the identity
matrix but T1,1has been enlarged by a factor of
a and T2,2 has been enlarged by a factor of b. = =
When multiplying by this matrix, the x co-
ordinate is enlarged by a factor of a, whilst
the y co-ordinate is enlarged by a factor of b.
12. Enlargment
Mathelaureate / IGCSE / Transformation / D.J Page no: 5
This transformation matrix creates a rotation
and an enlargement. When multiplying by this
matrix, the point matrix is rotated 90 degrees
anticlockwise around (0,0), whilst the x xo- = =
ordinate of the new point matrix is enlarged
by a factor of -5 and the y co-ordinate of the
new point matrix is enlarged by a factor of 7.
13. Streatch Horizontal axis stretch
k 0
0 1
Stretch, scale factor k parallel to the x- axis
Mathelaureate / IGCSE / Transformation / D.J Page no: 6
13. Streatch Vertical axis stretch
1 0 Stretch, scale factor k parallel to the y-axis
0 k
14. Shear Shear parallel to the x-axis
The matrix corresponds to a shear parallel to
the x-axis. Points on the x-axis do not move,
1 k whilst points on the line y = 1 are translated k
0 1
units to the right.
Mathelaureate / IGCSE / Transformation / D.J Page no: 7
15. Shear Shear parallel to y axis
The matrix corresponds to a shear parallel to
1 0 the y-axis. Points on the y-axis do not move,
k 1
whilst points on the line x = 1 are translated k
units up.
Mathelaureate / IGCSE / Transformation / D.J Page no: 8
You might also like
- Student Exploration: Uniform Circular MotionDocument5 pagesStudent Exploration: Uniform Circular MotionJoseph Chang80% (5)
- IB Business Management Section C SampleDocument1 pageIB Business Management Section C Samplepicboy83% (12)
- Oxford Math AA SL Exam Practise Additional ResourcesDocument172 pagesOxford Math AA SL Exam Practise Additional ResourcesSıla DenizNo ratings yet
- Jessie Pope "Who's For The Game" AnalysisDocument1 pageJessie Pope "Who's For The Game" Analysispicboy67% (3)
- 4PH1 2PR Rms 20190822Document14 pages4PH1 2PR Rms 20190822Åzmâñ Khäñ100% (3)
- Straight Line Graphs - Edexcel Past Exam QuestionsDocument8 pagesStraight Line Graphs - Edexcel Past Exam QuestionsAlisa PhanNo ratings yet
- IGCSE Mensuration FormulaDocument7 pagesIGCSE Mensuration FormulaBeshkaNo ratings yet
- MATH - Solving Trig EquationsDocument3 pagesMATH - Solving Trig EquationsjamesNo ratings yet
- Common Questions IGCSE Physics - Version 1Document3 pagesCommon Questions IGCSE Physics - Version 1RidwanAbrarNo ratings yet
- Transformation Geometry: Mark Scheme 1Document6 pagesTransformation Geometry: Mark Scheme 1anwar hossainNo ratings yet
- Gcse Data Work Book Compiled by MR BradfordDocument80 pagesGcse Data Work Book Compiled by MR Bradfordapi-655636980% (1)
- Moments Level 4-7Document2 pagesMoments Level 4-7docashisharoraNo ratings yet
- Mark Scheme (Results) January 2019: Pearson Edexcel International GCSE in Further Pure Mathematics (4PM0) Paper 01Document26 pagesMark Scheme (Results) January 2019: Pearson Edexcel International GCSE in Further Pure Mathematics (4PM0) Paper 01Mohammad Habibullah KhanNo ratings yet
- MathsDocument32 pagesMathsnour mohammedNo ratings yet
- 01 As Pure Mathematics Practice Paper ADocument6 pages01 As Pure Mathematics Practice Paper AFrankNo ratings yet
- Edexcel IGCSE Vector NotesDocument40 pagesEdexcel IGCSE Vector NotesÅzmâñ KhäñNo ratings yet
- Maths IGCSEDocument42 pagesMaths IGCSEPhelix_Young_640433% (3)
- A Level Mathematics - Practice Paper - 7.5 - Differential EquationsDocument6 pagesA Level Mathematics - Practice Paper - 7.5 - Differential EquationsZaka AhmedNo ratings yet
- Mathematics B 2020 January 1R PDFDocument23 pagesMathematics B 2020 January 1R PDFThuta100% (1)
- Mathematics M1 EDEXCELDocument10 pagesMathematics M1 EDEXCELballpoint96No ratings yet
- Edexcel Igcse Mathematics: DifferentiationDocument13 pagesEdexcel Igcse Mathematics: Differentiationමේනුක සූවින්දNo ratings yet
- IGCSE Maths 5080 SOW Core 3 YearsDocument16 pagesIGCSE Maths 5080 SOW Core 3 YearsYenny Tiga0% (1)
- Edexcel S2 Cheat SheetDocument12 pagesEdexcel S2 Cheat Sheetsushdhake5009No ratings yet
- GR 10-IG Maths Syllabus Overview 2020-21Document9 pagesGR 10-IG Maths Syllabus Overview 2020-21Paula HoNo ratings yet
- 9702 w17 QP 13 PDFDocument20 pages9702 w17 QP 13 PDFDhito PramudyaNo ratings yet
- Answers To Test Yourself Questions: Topic 6Document5 pagesAnswers To Test Yourself Questions: Topic 6Abel CruzNo ratings yet
- P1-Graphs and TransformationsDocument23 pagesP1-Graphs and TransformationsJumanaAsimNo ratings yet
- Cambridge IGCSE: MATHEMATICS 0580/21Document12 pagesCambridge IGCSE: MATHEMATICS 0580/21AbdullaNo ratings yet
- IB Related RatesDocument8 pagesIB Related RatesVidhiGondaliaNo ratings yet
- PDF Cambridge Igcse Core Mathematics 4Th Edition Ric Pimentel Ebook Full ChapterDocument53 pagesPDF Cambridge Igcse Core Mathematics 4Th Edition Ric Pimentel Ebook Full Chapterjackie.robinson980100% (3)
- Circular MeasureDocument27 pagesCircular MeasureRedzuan SaidiNo ratings yet
- CBSE Class 10 Maths Apr 13 Standard Sample Paper 2023 24Document9 pagesCBSE Class 10 Maths Apr 13 Standard Sample Paper 2023 24RAKESH SINGHNo ratings yet
- slws2 Oxford Answers Chapter 2 Ib Diploma SLDocument10 pagesslws2 Oxford Answers Chapter 2 Ib Diploma SLbibabibebuNo ratings yet
- Stats - 2022 CieDocument12 pagesStats - 2022 Cienan doeNo ratings yet
- Gcse Physics: CircuitsDocument21 pagesGcse Physics: CircuitsasifshahanaNo ratings yet
- GCSE Scince Bio Mixed QsDocument13 pagesGCSE Scince Bio Mixed QsSkyNo ratings yet
- WMA12 SampleDocument5 pagesWMA12 Samplejyf97ybqxyNo ratings yet
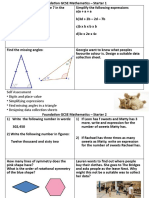
- Self Assessment - Digits and Place Value - Simplifying Expressions - Find Missing Angles in A Triangle - Designing Data Collection SheetsDocument23 pagesSelf Assessment - Digits and Place Value - Simplifying Expressions - Find Missing Angles in A Triangle - Designing Data Collection SheetsAlex GoldsmithNo ratings yet
- Dice Half Life ExperimentDocument1 pageDice Half Life ExperimentEsmond TangNo ratings yet
- EDEXCEL IGCSE Chemistry Practice Unit Test 1Document7 pagesEDEXCEL IGCSE Chemistry Practice Unit Test 1KasunDilshan100% (1)
- Space Physics IGCSE WSDocument53 pagesSpace Physics IGCSE WSaliyameen2006No ratings yet
- A Level Mathematics Practice Paper B - Pure MathematicsDocument8 pagesA Level Mathematics Practice Paper B - Pure MathematicsZaka Ahmed0% (1)
- Vectors in MechanicsDocument27 pagesVectors in Mechanicsmaryam ahmedNo ratings yet
- Revision Sheet of GCSE Trig TransformationsDocument3 pagesRevision Sheet of GCSE Trig TransformationsboobooNo ratings yet
- MockB HL P2 2015v1 Sect A OnlyDocument11 pagesMockB HL P2 2015v1 Sect A OnlyDhruvin DoshiNo ratings yet
- TA Properties of QuadrilateralsDocument3 pagesTA Properties of QuadrilateralsArindam BiswasNo ratings yet
- DFMFullCoverage-PythagorasTheorem 2Document12 pagesDFMFullCoverage-PythagorasTheorem 2M MNo ratings yet
- Binomial Theorem Cheat Sheet: N B N B N B N R B N! R! (N R) !Document1 pageBinomial Theorem Cheat Sheet: N B N B N B N R B N! R! (N R) !Mihir JainNo ratings yet
- Math IA 1Document22 pagesMath IA 1Vipul KurapatiNo ratings yet
- MockB HL P2 2015v1 Sect A Only PDFDocument11 pagesMockB HL P2 2015v1 Sect A Only PDFYoonseo ChoiNo ratings yet
- Chapter08 Deformation of Solids SsDocument6 pagesChapter08 Deformation of Solids SseltytanNo ratings yet
- Function: Edexcel IAL A Level Pure Mathematics 3 Revision NotesDocument28 pagesFunction: Edexcel IAL A Level Pure Mathematics 3 Revision NotesPrince YugNo ratings yet
- Thomas Moore AssessmentDocument11 pagesThomas Moore Assessmentshidik286No ratings yet
- Chapter 1: Movement and PositionDocument12 pagesChapter 1: Movement and Positionailsa3leungNo ratings yet
- Aqa Physics 2 Revision NotesDocument66 pagesAqa Physics 2 Revision NotesAsif UllahNo ratings yet
- Edexcel M1 Summary NotesDocument7 pagesEdexcel M1 Summary NotesAlexanderBrazdaLorenteNo ratings yet
- Caie Igcse Maths 0580 Theory v2Document16 pagesCaie Igcse Maths 0580 Theory v2Melis Doğu BayazıtNo ratings yet
- Geometrical ShapesDocument31 pagesGeometrical ShapesAlanie Grace Beron Trigo100% (1)
- Chapter 5 Transformations of The Euclidean PlaneDocument14 pagesChapter 5 Transformations of The Euclidean PlaneLitoy ArquizaNo ratings yet
- Basic Transformations:: TranslationDocument8 pagesBasic Transformations:: TranslationprincejiNo ratings yet
- Module 3 - 2D Transformations - 1Document91 pagesModule 3 - 2D Transformations - 1Rajeswari RNo ratings yet
- CG Chapter 5Document15 pagesCG Chapter 5rajmaisuria111No ratings yet
- Rack WorksheetDocument24 pagesRack WorksheetpicboyNo ratings yet
- Lab 12Document5 pagesLab 12picboyNo ratings yet
- Lab 13Document1 pageLab 13picboyNo ratings yet
- Evaluation Strategy Project - Navnith RavindranDocument23 pagesEvaluation Strategy Project - Navnith RavindranpicboyNo ratings yet
- What Are Some of The Key Aspects of Reflective Practice in TeachingDocument2 pagesWhat Are Some of The Key Aspects of Reflective Practice in TeachingpicboyNo ratings yet
- Final2012 PDFDocument5 pagesFinal2012 PDFpicboyNo ratings yet
- Intro CAD (Electrical) - Instructions For Assignment #2 DUE: End of Class Next Week InstructionsDocument1 pageIntro CAD (Electrical) - Instructions For Assignment #2 DUE: End of Class Next Week InstructionspicboyNo ratings yet
- Design 2Document9 pagesDesign 2picboyNo ratings yet
- Final 2012Document5 pagesFinal 2012picboyNo ratings yet
- Valley of Ashes DescriptionDocument2 pagesValley of Ashes DescriptionpicboyNo ratings yet
- LBCBDocument3 pagesLBCBpicboyNo ratings yet
- Film AnalysisDocument2 pagesFilm AnalysispicboyNo ratings yet
- IB Physics IA IdeasDocument1 pageIB Physics IA Ideaspicboy38% (8)
- Calculus by Thomas Finney 10th Edition Solution Manual Part IDocument828 pagesCalculus by Thomas Finney 10th Edition Solution Manual Part Ipicboy67% (3)
- SL IA Sample ADocument7 pagesSL IA Sample ApicboyNo ratings yet
- IB Command Terms - Categorized by Skill LevelDocument6 pagesIB Command Terms - Categorized by Skill LevelpicboyNo ratings yet
- Lesson 6: Black Holes: Notes From Prof. Susskind Video Lectures Publicly Available On YoutubeDocument50 pagesLesson 6: Black Holes: Notes From Prof. Susskind Video Lectures Publicly Available On YoutubenompanemNo ratings yet
- 02 # Race (With Solution)Document7 pages02 # Race (With Solution)rajeev ranjanNo ratings yet
- Blackhole MandelbrotDocument12 pagesBlackhole MandelbrotWilliam H SinerisNo ratings yet
- Testing Packet - Momentum and ImpulseDocument9 pagesTesting Packet - Momentum and Impulsekristaw7No ratings yet
- Kelm110 PDFDocument35 pagesKelm110 PDFDeepak pandeyNo ratings yet
- Physics For Scientists and Engineers, 6e: Chapter 15 - Oscillatory MotionDocument19 pagesPhysics For Scientists and Engineers, 6e: Chapter 15 - Oscillatory Motionaisyah syazwaniNo ratings yet
- Science: Quarter 3 - Weeks 1 - 2Document22 pagesScience: Quarter 3 - Weeks 1 - 2Maljan CorpuzNo ratings yet
- Relativity K Calculus MethodDocument17 pagesRelativity K Calculus MethodSourav RudraNo ratings yet
- Statics Course NotesDocument274 pagesStatics Course NotesSubin Idikula100% (1)
- DJJ5113 - Mechanics of Machines NotesDocument63 pagesDJJ5113 - Mechanics of Machines NotesAfiq Fahmi100% (1)
- Code Red - The Coming Destruction of America 2004Document126 pagesCode Red - The Coming Destruction of America 2004Biblio100% (21)
- Exercises: 4.1 Motion Is RelativeDocument4 pagesExercises: 4.1 Motion Is RelativeamilcarsoaresNo ratings yet
- Multivariable Calculus AssignmentDocument2 pagesMultivariable Calculus AssignmentGaussCVNo ratings yet
- Kinematics: Pre-Medical: Physics AllenDocument3 pagesKinematics: Pre-Medical: Physics AllenDivya AgarawalNo ratings yet
- Operation Guide 5202: About This ManualDocument6 pagesOperation Guide 5202: About This ManualMuhamad IrvanNo ratings yet
- Q4adphymodulewith Worksheet InsertionsDocument53 pagesQ4adphymodulewith Worksheet InsertionsKean CardenasNo ratings yet
- Chapter-2 Emf by SadiqueDocument35 pagesChapter-2 Emf by SadiqueAnonymous 4bUl7jzGqNo ratings yet
- 2012-1813. DH Representation - ExamplesDocument42 pages2012-1813. DH Representation - Examplesmodisuryaharsha100% (1)
- 07 Dynamics-Newton's 1st LawDocument2 pages07 Dynamics-Newton's 1st LaweltytanNo ratings yet
- DIRD 13-DIRD Warp Drive Dark Energy and The Manipulation of Extra Dimensions PDFDocument34 pagesDIRD 13-DIRD Warp Drive Dark Energy and The Manipulation of Extra Dimensions PDFypie01No ratings yet
- Einstein and Poincare - The Phys - Valeri v. Dvoeglazov (Editor)Document193 pagesEinstein and Poincare - The Phys - Valeri v. Dvoeglazov (Editor)mayra_patiño100% (1)
- Salvatore Giandinoto - Incorporation of The Golden Ratio Phi Into The Schrodinger Wave Function Using The Phi Recursive Heterodyning SetDocument2 pagesSalvatore Giandinoto - Incorporation of The Golden Ratio Phi Into The Schrodinger Wave Function Using The Phi Recursive Heterodyning SettheherbsmithNo ratings yet
- Graph Matching Lab-2Document6 pagesGraph Matching Lab-2Ajeet Singh100% (2)
- Abhay Ashtekar - Introduction To Loop Quantum Gravity (2011) (Ingles)Document30 pagesAbhay Ashtekar - Introduction To Loop Quantum Gravity (2011) (Ingles)Joaquin SanchezNo ratings yet
- Applications of Analytic GeometryDocument15 pagesApplications of Analytic GeometrydaniloNo ratings yet
- Dynamics YEADocument24 pagesDynamics YEAEllen KohNo ratings yet
- Motion-Distance and DisplacementDocument41 pagesMotion-Distance and Displacementmjdemaala100% (1)
- Physics114A L27Document25 pagesPhysics114A L27HendraKurniawanNo ratings yet
- Physics Research PaperDocument4 pagesPhysics Research PaperAngelajhoieNo ratings yet