Ewinwing thon 2 EHAPTER 3) A Graphical Solution Scorereeceeerrte Procedure and Further i Pre 1974 sean Examples S.A NTRCDUCTION In this chapter we continue to explore th linear programming problem anc its viriatons but we also provide a first method of solution. Te solution procedure tee describe is oaey to uneretan, at tose, we need ores Our attention (0 problems with wo, or at most three decision variables Such problems do occur but aey, and may be contrived. Nonetheless, the procedure demonstates that tse problems can be rolved. More importantly the procedure provides extremely vals: be insights about the geometric and mathematical properties of solutions ti ‘et: programming problems Using the set of geomettc and mathematical insights fsa foundation, we present in Chapter & a general algorithmic procedure that an be wed to solve any linear program, This general procedure, as we will point out atin, can be implemented by hand but, more signifienntly, can also be Coded for conputer solution. Tincontas, the method of solution demonstrated in this chapter i graphical nature We apply ito two ifferent problems the st (Example 1) i problem of ‘inaging a materials production operation, and the second (Example 3.2) i a problem that eck to allocate work efor efficiently between two mines Although fhe two models we formulate to demonstrate the graphical soltion procedure are (qt diferent, ther basic strtures st well asthe solution procedure used to salve | themodels are identical Tis second example is then extended as Extnpe 33nd the formulation s modified to incorporate a nonlinear objective function. «“ [AGraphicel Solution Procedure and Further Examples Chap. 3 {a addition to solving these small linear programs, we also present several “addtional problems and. model formulations in this chapter (Examples 3-4 through 21). Although these additional problems are 100 lange to be solved traphically they represent additional examples of the flexibility and wide applic- bility ofthe lear program for use in engineering management. Later chapters wil preseatsstematie procedures for solving these increasingly sophisticated ‘management models. 13.8 SOLVING LINEAR PROGRAMS GRAPHICALLY 3.8.1 Example 3-4; Homewood Masonry—A Materials Production Problem Problem Statement. Homewood Masonry sa small owner-operated fim that prodges onstruction materials forthe residential and commercial construc- tion industry inthe region. The company specializes in the manufacture of wo twidely used building prodts: (1) a universal conrete patching product calles HIYDIT and (a decorative brick mortar called FILIT. These products ar in great ‘demand, and Fomewood can sell al ofthe HYDIT it produces fora profit of $140 pet ton and allthe FILIT Itcan produce for a profit of $160 per ton ‘fortunately, some of the resources needed fo manufacture these products are in imited supply. Fs, the demand for both H'YDIT and FILIT is du in arge part to thelr fecal adhesive characterises, which result from the wse ofa specat Fopredient in the blending procese Wabash Red Clay (fom the banks of the ‘Wabash River nTndiana) Each ton of HYDIT produced quires cubic meters of this ed ly. and each ton ofFILIT produced requires 4 eubie meters "Wabath Red Clay is in limited supply; a maximum of 28 cubic meters ofthe clay i avallable each week. Second, tbe operator af the machine wed to blend these ‘products can work ony maximum of SO ours per week. This machine blends ton [teither prodect ta time, andthe blending process requires 5 hours to complete ‘asteach material mast be stored ina separate curing vat further limiting the over fl production volume of each product The ering vats for HYDIT and FILIT have {apecties of 8nd 6 tons respectively. These resource imitations are summarized in Table 31. ARES RESOURCE REQUREMENTS AND AVAILABLITY FOR THE HOMEWOOD ‘Wit Re Sip Zee Tah ae Coragratercig [sees T 50.38 Sot You have the material pre ‘wood Masonry Model F Homewood M: problem as pre: Sons that we ‘case, the objet make each wee satisfying four 1 The total week: 2, The blend 3 The sora & The sors, Fora given sol ‘ons simultane the langst vale ming formulat function wee To transis the decision vi furelves the f facture of HYT tion engineer € product sold ( fesouroes AS t much ofeach p Let We may now y follows This expresior problem solutexamples Chap. alo present sever loyter (Examples 3-4 vo large to be soled bility tnd wide applic sue. Later capers euingly sophisticated I owner operated frm {commercial consric: ve manufacture of (0 fcting product called se products are in great ‘eestor a profit ef $140 perton, iigcure these products AF-LIT is due in arge fom the use of a speci rom the banks of the quires 2 cubie meters of 28 subic meters ofthe Lincused to blens these ‘amachie blends aton ex Shouts to complet. her imiting the over tioavare sommarzed in Sec.8.8 Solving Linear Programs Graphically “ ‘You have been hited to help with the development of a strategy fr operating the material production process What i the optimal production strategy for Home ‘wood Masonry given these data? ‘Model Formulation. The formulation of a production model for the Homewood Masonry problem begine by translating the major elements of the problem as presented above into pseudo mode, a word description of the equ fons that we will ned to capt the importat elements ofthe problem I this case, the objective of our model i t determine the amount of each product {0 make each week so as to maximize the overall profits resulting fom sales, wile ‘atistying four production conditions week 2. The blending machine cannot be used for mote than SO hours per week 3. The storage capacity for HYDIT may not be exceeded each week: nd 4 The storage capacity for FILIT may no be exceeded each week, Fora given solution to be feasible it must stay al four ofthese constraint cond. tion simultaneously Fora give solution tobe opti, it must, in addition, provide ‘the largest value for the objective function (tal profit). For aay linear program: ‘ing formulation, the constrain elatonships define feasibly, while the Objective function i used to determine optimality ‘To translate the pseudo-model into a linear program it i necessary to define the decision variables that wil be used in the model In this case we might fis sk ‘ourselves the following question: In determining a production poiy forthe man facture of HYDIT and FILIT, what i these of decision variables thatthe produc tion engineer controls? Clearly he engineer does not control proit-per-volume of ‘product sold (atleast not directly), nor does helshe control the avalabiliy of Tesourees. As the problem i stated, the engineers faced with the decision of how ‘uch ofeach product to manufacture. Indeed, we asume that he eagineet ha (otal control over, and responsibilty for, this decision, Let:xy = the mumber of tons of HYDIT to produce each week. 2, the number of tons of FILIT to produce each week ‘Wie may now write an expression for total profit as a function of weekly sales as follows total weekly profi Mor, + 160%, ‘or, writen as the objective function for our model, Marimize Z = 140s; + 160%, ‘This expression wil be used to evalute a (generally, very large) numberof feasible problem solutons,“ Graphical Solution Procedure and Futhor Examples Chap.3 We can use these decison variables to write general expressions that wil relate any possible level of production tothe resulting level of resource wage For trample, te total volume ofthe red cla rexource that wil be wed fora given prov ‘veto strategy ia linear function of production volumes of our two materials as preseted in Table 31 total ed cay wed = 21 + 4, Because our production strategy may be constrained by the avalabilty ofthis ma terial our model mus include an expt constrain the consumption of ed cay $day = 28 Similarly we can write expressions forthe urage ofthe blending machine as fone tion of production: total blending machin time = Sxy + Sx or written as tnear constraint Su + 54 = 50. Finally, two additional model constraints will ensure that storage forthe materials vill not be exceeded HYDIT produced each week = 8 tons, FILIT produced each week = 6 ons, 48, ' 56. The complete linear program forthe Homewood Masonry production model may now be presented Maximize Z = 140xy + 160% Subjectto: 2x, + 4x Si + 5m, = 50 E The ls term in ou formulation restricts our decision variables fom taking on neg. stive values Negative production of oe type of materials not physically feasible {ven though doing 40 ina theoretical sense might result in more resources being S038 availa of decid decision Be probes present aB2A Problen treause mapped verlable tte opti c inFigun ont (x). Al taning olthese ‘wl all sesy thverExamples Chap. al expressions that will Slt resource usage. For ‘bewsed fra given pro- sol our two materials as co svalabilty of thie ma- consumption a rd day acingmachine a5 2 fone: storage forthe materials ssonry proacton model able Srem taking on nee Sot physically feasible in more resources being, Sec. 8.8 Solving Linear Programe Graphically ” avilable to manufacture an addtional amount ofthe other material Non-negatvty Of decison variables san important assumption that willbe more fly appreciated ‘when we discas the lgoritim used oslve linear progr having large mumbo ot ‘decision variables Because this model formulated to solve the Homewood Mascar production problem uses only two decision variables, we can aove this problem graphically as resented in 3.82, 3.8.2 AGraphical Solution for the Homewood Masonry Problem Problems containing fewer than four decison variables can be solved graphically bbeause the solution space for al possible combinations ofthese variables can be ‘mapped into space inthe case of two variables and space in the cate of three vaiabes. 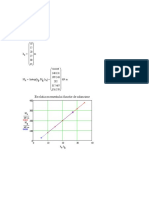In ition, that solution space can be further partitioned by plowing the onstrant equations Finally the objecave function can be plotted and wed to find ‘the optinal solution, ‘Cansders solution space forthe Homewood Masonry problemas presented {n Fgure 3.1, where the total volume of production of HYDIT is ploted on the hor ‘zontal ais (x), and the total volume of production of FILIT oa te versal axis (22) All posible combination of production levels can be epreseted within this space Next, sch constraint equation from our model can be plot as 3 Hne con ‘aining al points that stisty that equation with tit equa. Al pomts on one sie ‘ofthese ines—the side indicated by the open arrow satis the orignal inequality, while allpoins on the other side ofthese lines violate that constraint Inthe eae of fan equality constraint, only point falling diectly on the coresponding line would Satis tht condition pret, Fele taste “Tat HVDIT np) ‘aeAGraphice! Solution Procedureand Further Examplos Chap. ‘The femible region for a linear program is defined asthe set of solutions (values forthe decision variables) that satisfy al constraint equations including ‘on-nesaivity conditions simultaneously. The faible region forthe Homewood ‘Matonry problem is thus the shaded area of Figue 3.1, Convince yourself thatthe solution space fra linear program will always eansst of oe af three possiblities (2) an infinite number of fasbe solutions, 2) asingle feasible solution, or (3) > Solutions (tis possible that no point sats all xnstrins). ‘After the feasible region has ben identified (graphed), the objective fonction can be sed to evaluate all feasible solutions Figure 3.2 shows the feasible region for ‘he Homewood Masonry problem withthe objective function, Z = 14, = 160%, plotted at four different locations in decison space Z = 0, Z = S60,Z = 1120, and 1Z'= L480, Note that each ofthese dote lines i parallel to all of the others This is ‘because regardles ofthe vale of the objective function at particular solution, the slope ofthe objective function line is constant, determined by the coefficients ‘tat multiply the dessin variables inthe objective function, "At the lower lefthand portion of Figure 32, the line representing the objec tive fntion i plotted pasing through the origin (xj = O, xz ~ 0) such hat each point on thi line will produces valve of ero forte objective function Z. Note that fhe only point on thi in segment that i easbbe (intersects withthe feasible re ilo in decision apace) se ni ‘Next we plot the objective function gradient passing through the points (4,0) and (0,33) These points as well a al points on tht ine, result na valu forthe ob- jective function of 560, which, becuse we ae matimizing the objective function, is fan improvement over the fst objective fonction Furthermore there are an infinite ‘umber of feasible goltions that give this same value forthe objective function—all points onthe ine epment joining (4,0) with (0,35) ae feasible and give an objective uy 2 As echt int Sec 38 function dleated at all pe that pro point is ‘Sbvious Tem wer function the edt have oe T practica mously The oor robles 3837) ‘Whenes be one oped w these Pr ¥y prob @plou the obje feasible regione Tine tha nal sel uigue « ‘ae slt‘Examples Chip.3 a he st of soltions 2X gut isang joniorthe Homewood arin yous ha the te of ee ponies Shi solution or (a0 , te bjs ncton nite rein for mud = Min + Ory 2 sco,2 = mh “alot the others Tis ‘aril ston the ited bythe cocticens: Vepmetentng the oe: eee op sth tat ach ‘hintionZ Nott Sth te fener throreh the points (0) sulin valu forthe ob- toe tere are an infnite ‘cobectve incton—alk ble and give an objective soest Opin / Sec.3.8 Solving Linea Programs Graphically « function vale of 60. We continue to “move” the objective function line inthe rection ofimprovement—ypwards and to the right inthis case (or Northeast) ein dicate by the slid artow ear the “Dizection of Objective Function Improvement” notation oo the graph ‘As we move the line, we can graphically evaluate the objective function value at all points inthe fesibie repion. Taat point where the objective funtion, i ts ‘movement to the Nortteast last intersects the feasible region ithe fesbleslation that provides the best (optimal) value of Z while stil satisfying all problem com straints This points thus the opal solution to this probes ia this example, thet point is xy = 6,1, ~ ¢ with an objective function value Z = 1480. It should be ‘obvious that the poin: x; = 0.x, = 0 would be the optimal solution ifthe probs Jem wer mininiraton problem, diough the feusbe region and the obyecuve function line would be the Same, Note, alo, that the optial solution occured "on the edge” of the easitleregion—in tis situation at just a pont, although it might have occurred along line (or in 3space along s plane). The optimal solution, turns out, wil always occur at a point an edge or a plane ‘The models that canbe solved graphically are generally too smal o be of practical value, Nonetheless the visual soltion procedure just desibed is enor ‘mousy important in understanding how analytial solution methodologies work ‘The concepts of feasiilty and optimality are precisely the same regardless of problem size And the vocrrence ofthe solution alonga plane or line or at point ‘aries over othe largst of problems. 1.3 Types of Linear Programming Solutions ‘Whenever a linear pregramming mode! is formulated and solved, the result will bbe one of four characteristic solution types. The graphical framework just devel ‘oped while solving the Homewood Mavonry probiem is useful for visualizing thee solution types Problems Having Unique Optima. The soto tothe Homewood Mason ty probiem was achieved by (1) graphing the feasble region in deciion space, {Q) plotting the ine of te objective function onthe same graph, and (3) then shifting {he objective function line inthe dizection of improvement unit st itersected the feasible region (se Figure 3a). In this case the intersection between the feasible region andthe set of points satistying the equation Hox, + 160, = 1480 ‘consisted ofa singe pent x, = 6 and x = 4. Tis point is the only point on this line that satisis all constraint equations simultaneously. Consequeat the opt ‘al solution tothe linear program sa unigue one the solution i ai to have a tnigue optimum or unique optimal solution. Its possible, however, that mote than ‘one solution (perhaps a infinite numberof solutions) would be optimal,C ‘Graphs! Soliton Procedure and Further Examples Chap. ies bet et tien te bathe oo an) protests ebeande Problems Having Alternate Optima, As demonstrted in the previous section, the orientation ofthe objective function in dessin space is determined by the coticients that multiply the decision variables For example ifthe coeicient of ‘in the original objective function is decreased relative othe coefficient on, the Slope or gradient becomes steeper (more negative). Suppose the orginal objective funtion were replaced by Maximize M03, + 140 1d the problem were resolved graphically. Then the intersection ofthe objective function ine andthe feasible region at optimality becomes aie segment as shown 00.98 i Figur @2yie ™ Inve Tear p inoud oonditio kena Pr feasive when 20 forma felution Fy space ie infeasin dbtecta larger mulated Pr pobler preecte oven: face, fnetion andtot! fan ako Tike int ‘spoemy oundee soeverExameles Chap. Fue pets ba statec in the previous im spaceis determined by imple ifthe eoelficent of ‘ore the orignal objective nection of the objective Saline segment as shown ec.38 Solving Linear Programs Graphically st in Figure 33, and all points onthe line segment connecting the points (64) and (82) yield the same value fr the objective funtion and sais the equation Moxy + 140e; = 1400 ‘Tis problem thus has an infinite numberof optimal solutions, oF ssid to have altemate optima. Alternate optima ae actually more common asthe sie of the linear programmng probiem (aumber of decision variables end constraint) in teases and it sc vale to be able to recognize thee presence It wil be important {nour dscusion of a general solution procedure for near programs to dently the ‘conditions that sgal the presence of alternate optimal solutions This topic wil be taken up in Chapter Problems Having No Feasible Solution. Its posible that there ce no feasible solutions fora given problem formulation. This can occur quite naturally when constrains confit with one another, ofthe condition may be duet errors in formulating logcl constraints Such a condition can also our because of sakes in entering a problem formulation toa model solver (computer progam). In any vent the problem is observed to be overconsrained to the extent that there's 80 Solution satistyng all constraints simultaneous Figure 3. shows three constraints of a hypothetical model plotted in decsion space in such a vay that there i no feasible toltion; the problems suid fo be infeasible, When slving linear programs graphically, infeasible solutions ae ex